Potter T.D., Colman B.R. (co-chief editors). The handbook of weather, climate, and water: dynamics, climate physical meteorology, weather systems, and measurements

Подождите немного. Документ загружается.

Equilibrium Between Ice and Vapor

Similarly, for equilibrium between ice and vapor, we can write

d ln e

; ð19Þ

where we again take l

to be the absolute value of the difference in enthalpy between

the vapor and solid phase of water.

Computation of Saturation Vapor Pressure (e

and e

)

For a preci se integration of the Clausius–Clapeyron equation, one must consider the

latent heat variation with temperature. To a good ﬁrst approximation, let temperature

be independent of latent heat and then integrate, yielding

ln e

¼

þ const: ð20Þ

This formulation has assumed latent heat to be independent of temperature. This is a

good approximation for sublimation, but not as good for freezing or condensation.

We can improve on this by using a more precise formulation for latent heat variation

and speciﬁc heat variation with temperature with a series expansion:

ln e



þ Da ln T þ

T þ

þ



þ const : ð21Þ

where the integration constant is determined empirically.

We need not achieve this much accuracy for most meteorological considerations,

since we cannot measure vapor pressure that precisely anyway. Hence we can make

approximations that allow us to calculate e

or e

with sufﬁcient accuracy. Here are

three approximations:

1. Solving the constant at the triple point temperat ure ðT

Þ, and assuming latent

heat constant, we obtain

¼ 10

ð9:40512354=T Þ

¼ 10

ð10:55532667=T Þ

2. Assuming heat capacity constant and retaining two terms in a series, we get

Magnus’s formula (liquid–vapor only):

¼ 10

ðð2937:4=T Þ4 :9283 log T þ23:5518Þ

ð22Þ

216 MOIST THERMODYNAMICS

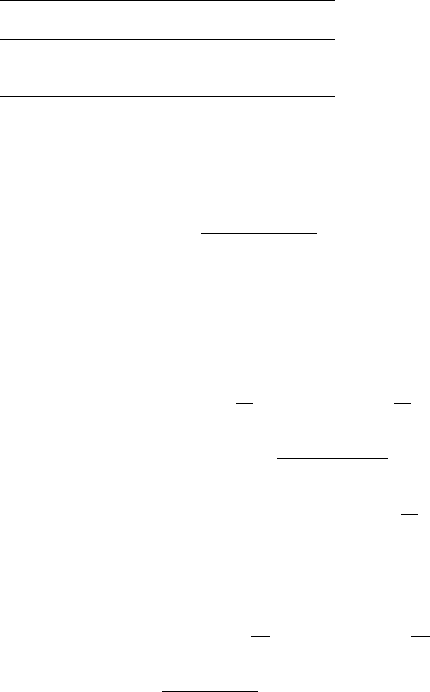
This has been simpliﬁed by Tetens (1930) and later by Murray (1966) to be

easily computed from the relationship (for pressure in millibars):

¼ 6:1078 exp

aðT  273:16Þ

T  b



ð23Þ

where the constants are deﬁned in Table 3.

3. Many atmospheric scientists use the Goff–Gratch (1946) formulation given

by:

¼ 7:95357242x10

exp 18:1972839



þ 5:02808 ln



 70242:1852 exp

26:1205253



þ 58:0691913 exp 8:039 45282



ð24Þ

for saturation over liquid where T

¼ 373:16 K. For saturation over ice:

¼ 5:57185606x10

exp 20:947031



 3:56654 ln





2:01889049



ð25Þ

where T

¼ 273:16 K.

Tables 4 and 5 show how the accuracy of Teten’s formula compares to Goff–

Gratch as reported by Murray (1966). Both of these forms of saturation vapor

pressure are commonly used as a basis to compute saturation vapor pressure.

5 GENERAL THEORY FOR MIXED-PHASE PROCESSES WITHIN

OPEN SYSTEMS

Often thermodynamic theory is applied to precipitating cloud systems containing

liquid and ice that often are not in equilibrium. In many thermodynamic texts,

the simplifying assumption of equilibrium is made that can invalidate the result.

TABLE 3 Constants for Teten’s Formula

Water Ice

a 17.2693882 21.8745584

b 35.86 7.66

5 GENERAL THEORY FOR MIXED-PHASE PROCESSES WITHIN OPEN SYSTEMS 217

Moreover, ice processes are often neglected, despite the existence of ice processes

within the vast majority of precipitating clouds. We will adopt the generalized

approach to the moist thermodynamics problem, developed by Dutton (1973) and

solve for the governing equations for a nonequilibrium three-phase system ﬁrst and

then ﬁnd the equilibrium solution as a special case.

TABLE 4 Saturation Vapor Pressure over Liquid

t (



C) Goff–Gratch (mb) Tetens (mb) Difference (%)

50 0.06356 0.06078 1:6  10

2

45 0.1111 0.1074 1:6  10

2

40 0.1891 0.1842 1:6  10

2

35 0.3139 0.3078 1:7  10

2

30 0.5088 0.5018 2:1  10

2

25 0.8070 0.7993 4:5  10

2

20 1.2540 1.2462 2:8  10

2

15 1.9118 1.9046 5:8  10

2

10 2.8627 2.8571 1:9  10

3

5 4.2149 4.2117 5:2  10

4

0 6.1078 6.1078 1:8  10

7

5 8.7192 8.7227 1:9  10

4

10 12.272 12.2789 2:2  10

4

15 17.044 17.0523 1:8  10

4

20 23.373 23.3809 1:1  10

4

25 31.671 31.6749 3:7  10

5

30 42.430 42.426 2:5  10

5

35 56.237 56.221 7:1  10

5

40 73.777 73.747 9:5  10

5

45 95.855 95.812 9:7  10

5

50 123.40 123.35 7:5  10

5

TABLE 5 Saturation Vapor Pressure over Ice

t (



C) Goff–Gratch (mb) Tetens (mb) Difference (%)

50 0.03935 0.03817 9:4  10

3

45 0.07198 0.07032 8:8  10

3

40 0.1283 0.1261 8:5  10

3

35 0.2233 0.2205 8:5  10

3

30 0.3798 0.3764 9:2  10

3

25 0.6323 0.6286 1:3  10

2

20 1.032 1.028 1:2  10

1

15 1.652 1.648 4:1  10

3

10 2.597 2.595 9:9  10

4

5 4.015 4.014 1:7  10

4

0 6.107 6.108 6:3  10

5

218 MOIST THERMODYNAMICS

Besides the nonequilibrium phase changes, the formation of liquid and ice hydro-

meteors create a heterogeneous system having components of gas, solids, and

liquids, each of which may be moving at different velocities. We must therefore

forego our traditional assumption of an adiabatic system and instead consider an

open system. In doing so, we ﬁx our coordinate system relative to the center of the

dry air parcel. Although we can assume that vapor will remain stationary relative to

the dry air parcel, we must consider movements of the liquid and solid components

of the system relative to the parcel, hence implying diabatic effects. We therefore

generalize the derivation of Eq. (4) to include these effects. It will be convenient to

work in the system of speciﬁc energies (energy per mass).

We will assume that our system is composed of several constituents, each of mass

. Then the total mass is

m ¼

: ð26Þ

We account for both internal changes ðd

Þ, which result from exchanges between

phases internal to the parcel, and external changes ðd

Þ, which result from ﬂuxes of

mass into and out of the parcel. The total change in mass is thus

¼ d

þ d

: ð27Þ

By deﬁnition and for mass conservation, we require

m ¼

¼ 0; and

m ¼

¼ d

þ d

As discussed above, external mass changes are restricted to liquid or ice consti-

tuents, while gas constituents are assumed not to move relative to the system. An

exception can be made, although not considered here, for small-scale turbulent

ﬂuxes relative to the parcel. From our original discussion of the ﬁrst law, we can

write the generalized form of Eq. (4) in a relative mass form as:

dH ¼ dQ þ VdPþ

ð28Þ

where h

¼ð@H

=@m

Þ. We found earlier that the terms involving h

eventually result

in the latent heat term.

We can split the heating function, dQ ¼ Q

þ Q

. Here Q

is the diabatic change

due to energy ﬂowing into or out of the system that does not involve a mass ﬂow. Q

accounts for diabatic heat ﬂuxes resulting from mass ﬂuxes into or out of the system.

The diabatic heat source of conduction between the parcel and an outside source

would be accounted for in Q

if no mass back and forth ﬂow into and out of the

parcel is not explicitly represented. Even the case of turbulent heat transfer into and

out of the parcel would not affect Q

unless the explicit ﬂuxes of mass in and out

were represented. The heat ﬂux associated with the movement of precipitation

featuring a different temperature than the parcel, into and out of the parcel, would

also be represented by Q

; as it would appear as a different enthalpy for the preci-

5 GENERAL THEORY FOR MIXED-PHASE PROCESSES WITHIN OPEN SYSTEMS 219

pitation constituent, and be accounted for by the d

term. As is conventional, we

will assume Q

¼ 0. Now;

¼ d

H  Vdp

; and ð29Þ

¼ d

H 

ðh

 hÞ d

: ð30Þ

We can similarly split the enthalpy tendency into its internal and external parts:

¼ Q

þ Vdp

; and ð31Þ

¼

ðh

 hÞ d

: ð32Þ

Ignoring the noninteracting free energies, Gibbs’ relat ion for the mixed-phase

system is written in ‘‘per mass’’ form as:

TdS¼ dH  Vdp



; ð33Þ

where m

is the chemical potential per mass rather than per mole as we ﬁrst deﬁned

it. We can now divide the entropy change between internal and external changes, and

employing Eq. (29)

S ¼ Q



; and

S ¼

;

ð34Þ

for the external change. Since, m

¼ g

¼ h

 Ts

, and Eq. (30), then

S ¼



: ð35Þ

Now we apply our results to the particular water–air system. Consider a mixture

composed of m

grams of dry air, m

grams of vapor, m

grams of liquid water, and

grams of ice. We require

¼ d

¼ 0;

þ d

¼ 0; and

¼ 0:

ð36Þ

220 MOIST THERMODYNAMICS

The internal enthalpy equation [Eq. (31) and internal entropy Eq. (36)] can then

be written for this mixed-phase system:

H ¼ Q

þ Vdpþ

; and ð37Þ

S ¼



: ð38Þ

For the air–water system Eq. (38) becomes

S ¼



; ð39Þ

where the a

and a

are the speciﬁc afﬁnities of sublimation and melting. They are

deﬁned as:

 m

 m

;

 m

 m

The afﬁnity terms take into account the entropy change resulting if the two inter-

acting phases are out of equilibrium. They would be expected to be nonzero, for

instance, if rain drops are evaporating in an environment where the air is subsatu-

rated. Under equilibrium conditions, they would vanish. An example is cloud drops

growing by condensation in an environment where the vapor pressure is equal to the

saturation vapor pressure over liquid. The afﬁnity is the Gibbs free energy available

to drive a process and unavailable to perform work. Notice the symmetry between

the afﬁnity declarations and the latent heat declarations.

If we apply Eq. (39) to adiabatic melting, condensation, and sublimation, we

obtain

Tðs

 s

Þ¼l

þ a

;

Tðs

 s

Þ¼l

þ a

; and

Tðs

 s

Þ¼l

þ a

ð40Þ

We can state that the total entropy is equal to the sum of the entropy in each system

component:

S ¼ m

þ m

; ð41Þ

where the dry air entropy is

 c

ln T  R

ln p

: ð42 Þ

5 GENERAL THEORY FOR MIXED-PHASE PROCESSES WITHIN OPEN SYSTEMS 221

We have required that the only external ﬂuxes are those of precipitation. Hence,

we ﬁnd

S ¼ dS  d

¼ dS  s

 s

;

¼ dðm

þ m

Þþs

þ s

þ m



ð43Þ

Combining Eqs. (36) and (40) with (4) we obtain:



 d

þ m



 m



þðm

þ m

Þ ds

: ð 44Þ

If we now assume that the liquid is approximately incompressible, then

¼ c

ðdT=TÞ. Deﬁning mixing ratio of the jth constituent as:



; ð45Þ

and divide Eq. (44) by m

. Then we obtain the following general relation:

ln T  R

ln p



 d



þ r



 r



þðr

þ r

Þc

: ð 46Þ

The differentials account for the interrelationship between temperature change, pres-

sure change, and liquid phase change. Additional diabatic heating tendencies by

radiative transfer, molecular diffusion, and eddy diffusion can be accounted for with

the internal heating term q

. Neglected are the effects of chemical reaction on

entropy, alth ough the heating effect can be included in the heating term. Generally,

these effects are small and can be neglected.

What is included are not only the latent heating effects of the equilibrium reaction

but the effects on heating resulting from the entropy change in nonequilibrium

reactions. Hence, since entropy change removes energy from that available for

work, nonequilibrium heating from phase change modiﬁes the enthalpy change

resulting from phase change. The afﬁnity terms ac count for these effects.

Notice that both afﬁnity terms are inexact differentials, implying that their effect

is irreversible. The heat storage term [last term on the left-hand side (LHS)] is also

222 MOIST THERMODYNAMICS

an exact differential if we neglect the variation of c

and we assume the total water,

deﬁned as:

¼ r

þ r

; ð47Þ

is a constant. If there is a change, i.e., a diabatic loss or gain of moisture by

precipitation, then the differential is inexact and the process is irreversible. This

term also contains all of the net effects of diabatic ﬂuxes of moisture for systems

that are otherwise in equilibrium between phases. The heating term, q

, is purely

diabatic and deﬁnes a diabatic thermal forcing on the system such as by radiative

transfer or molecular diffusion and turbulence.

Note that, although the ﬁrst term on the LHS is written as a total derivative, the

external derivative of the quantity in brackets is in fact zero. Hence all reversible

terms appear as internal derivatives while the reversible terms contain both internal

derivatives for moist adiabatic process and external derivatives for diabatic ﬂux

terms.

6 ENTHALPY FORM OF THE FIRST–SECOND LAW

We now derive what is perhaps a more commonly used form of Eq. (46). Whereas

Eq. (46) is in a form representing entropy change, it can be rewritten as an enthalpy

change. To do so we make some manipulations.

First, we make the following assumptions:

1. Neglect the curvature effects of droplets.

2. Neglect solution effects of droplets.

These assumptions are really quite unimportant for the macrosystem of ﬂuid parcels.

However, the assumptions would be critical when discussing the microsystem of the

droplet itself, since these effects strongly inﬂuence nucleation and the early growth

of very small droplets. With these assumptions, the chemical potential of the vapor is

deﬁned:

¼ m

þ R

T ln e

; ð48Þ

where e

is the atmospheric partial pressure of the vapor. The chemical potential of

the liquid and ice are deﬁned as the chemical potential of vapor, which would be in

equilibrium with a plane pure surface of the liquid or ice and are given by:

¼ m

þ R

T ln e

; ð49Þ

¼ m

þ R

T ln e

; ð50Þ

6 ENTHALPY FORM OF THE FIRST–SECOND LAW 223

where e

and e

are the saturation vapor pressures of the ice and liqu id deﬁned by the

temperature of the liquid or ice particle. This temperature need not be the same as

the vapor temperature T for this equation.

Combining the equation of state applied to vapor and to dry air, it can be shown

that:

d ln pðR

þ r

Þ¼R

d ln p

þ r

d ln e

: ð51Þ

Combining Kirchoff’s equation (5), with Eqs. (46) to (51) and (18) and (19),

d ln T  R

d ln p þ



ð52Þ

where c

¼ c

þ r

is the effective heat capacity of moist air and

¼ R

þ r

is the moist gas constant (not to be confused with the gas constant

of moist air).

Although Eq. (52) appears different from Eq. (46), it contains no additional

approximations other than the neglect of the curvature and solution effects implicit

in the assumed form of che mical potential. It is simpler and easier to solve than the

other form because the afﬁnity terms and latent heat storage terms are gone. Note,

however, that there are some subtle inconveniences. In particular, each term is an

inexact differential that means that they will not vanish for a cyclic process. This

makes it more difﬁcult to integrate Eq. (52) analytically. Nevertheless, it is a conve-

nient form for applications such as a numerical integration of the temperat ure change

during a thermodyn amic process.

Some of the effects of precipitation falling into or out of the system are included

in Eq. (52) implicitly. To see this look at the change in vapor. It is a total derivative

because only internal changes are allowed. The ice change, on the other hand, is

strictly written as an internal change. Hence it is the internal change that implies a

phase change, and knowing the ice phase change and liquid phase change, the liquid

phase change is implicitly determined since the total of all internal phase changes are

zero. Since, by vir tue of the assumption that a heterogenous system is composed of

multiple homogenous systems, we assumed that hydrometeors falling into or out of

the system all have the same enthalpy as those in the system itself, there is no

explicit effect on temperat ure.

This assumption can have important implications. For instance, frontal fog forms

when warm rain droplets fall into a cold parcel, hence providing an external ﬂux of

heat and moisture through the diabatic movement of the rain droplet relative to the

parcel. We neglect this effect implicitly with eq. (52). By requiring

H ¼

ðm

Þ¼

, we only considered the external changes due to

an external ﬂux of water with the same enthalpy of the parcel. The neglect of these

effects is consistent with the pseudo-adiabatic assumption that is often made. That

assumption assumes condensed water immediately disappears from the system, and

so the heat storage effects within the system and for parcels falling into or out of the

system can be neglected. So far, the pseudo-adiabatic assumption has only been

224 MOIST THERMODYNAMICS

partially made because we still retain the heat storage terms of the liquid and ice

phases within the syst em. It is unclear whether there is an advantage to retaining

them only par tially.

7 HUMIDITY VARIAB LES

Water vapor, unlike the ‘‘dry’’ gases in the atmosphere exists in varying percent ages

of the total air mass. Obviously, deﬁning the amount of vapor is critical to under-

standing the thermodynamics of the water–air system. We have developed a number

of variables to deﬁne the vapor, liquid, and ice contents of the atmosphere. Below is

a list of the variables used to deﬁne water content.

Vapor Pressure (e

)

Vapor pressure represents the partial pressure of the vapor and is measured in

pascals. The saturation vapor pressure over a plane surface of pure liquid water is

deﬁned to be e

while the vapor pressure exerted by a plane surface of pure ice is e

Mixing Ratio and Speciﬁ c Humidity

We have already introduced mixing ratio to be r

¼ r

, and employing the

equation of state, we can relate mixing ratio to vapor pressure:

p  e

ð53Þ

where E  M

. We deﬁne speciﬁc humidity to be the ratio of q

¼ r

=r.It

follows that

1 þ r

Then, similar to Eq. (53) we can write for speciﬁc humidity:

ð1 þðr

=EÞÞ

ð54Þ

To a reasonable approximation, one can show that e

 p and hence:

 r

 E

ð55Þ

7 HUMIDITY VARIABLES 225