Потапенко Е.М., Казурова А.Е. Основы теории автоматического управления
Подождите немного. Документ загружается.

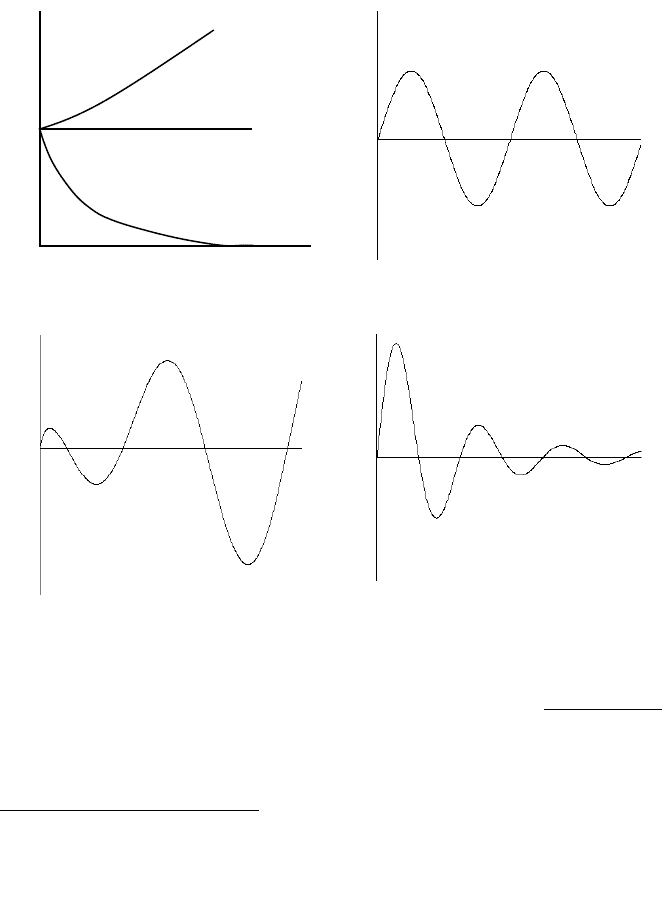
Рисунок 1.8.4
Для того чтобы система была неустойчивой, достаточно,
чтобы хотя бы у одного корня действительная часть была
положительной.
Для того чтобы система была гранично устойчивой,
необходимо и достаточно, чтобы у части корней действительные
части были равны нулю, причём среди этих корней не должно быть
кратных, а у остальных корней действительные части должны
быть меньше нуля.
При наличии кратных корней (например,
31321
pppp
)
вместо выражения (2) будет выражение (5).
k
<0
k
>0
β
k
= 0
t
β
k
= 0
y
сk
0
k
=0
а)
α
k
=0
β
k
≠0
y
сk
0
t
б)
α
k
> 0
β
k
≠ 0
y
сk
0
t
в)
α
k
<0
β
k
≠ 0
y
сk
0
t
г)
y
y
y
tc,
y
y
y
y
t
0
t
0
41
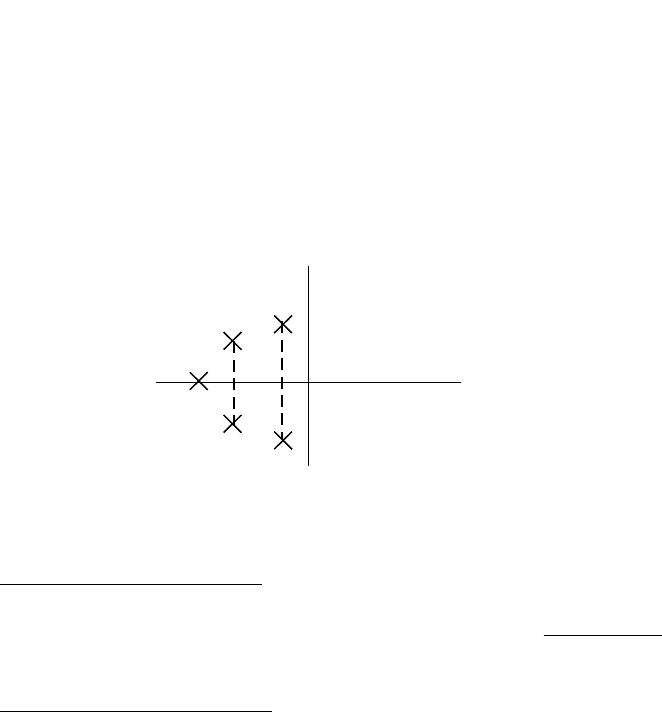
tp
n
tp
tp
c
n
ececetctccy
4
31
4
2
321
)(
. (1.8.1.5)
Выражение (5) позволяет заключить, что при мнимом корне
31
p
нулевое решение будет неустойчивым за счет выражения в
скобках.
Сформулируем приведенные критерии в геометрическом виде.
На рис. 5 изображена плоскость корней, где крестиками обозначено
расположение корней. С помощью этого рисунка приведенные
критерии можно перефразировать следующим образом.
Рисунок 1.8.5 – Расположение корней в случае асимптотической устойчивости
Для того чтобы система была асимптотически устойчивой,
необходимо и достаточно, чтобы все корни характеристического
уравнения находились в левой полуплоскости.
Для того чтобы система была неустойчивой, достаточно,
чтобы хотя бы один корень находился в правой полуплоскости.
Для того чтобы система была гранично устойчивой,
необходимо и достаточно, чтобы часть корней находилась на
мнимой оси, причём среди этих корней не должно быть
совпадающих, а остальные корни должны лежать в левой
полуплоскости.
1.8.2 Коэффициентные (алгебраические) критерии
устойчивости
Как следует из предыдущего пункта, устойчивость или
неустойчивость системы зависит от корней характеристического
уравнения, в свою очередь, корни зависят от коэффициентов
0
y
y
y
tc,
y
y
y
y
t
0
t
0
42

характеристического уравнения, поэтому естественно желание найти
критерии устойчивости без расчёта корней, рассматривая
непосредственно коэффициенты характеристического уравнения.
Среди большого количества коэффициентных критериев
устойчивости будем рассматривать два:
1) критерий о необходимых условиях устойчивости;
2) критерий Рауса-Гурвица.
1.8.2.1 Критерий о необходимых условиях устойчивости
Для того чтобы система была асимптотически устойчивой,
необходимо, чтобы все коэффициенты характеристического
уравнения были одного знака и отличались от нуля.
Пример. Дано уравнение
1472065
)4(
yyyyy
.
Это дифференциальное уравнение допускает частное
стационарное решение
2,147 yy
.
Задача: будет ли частное (вынужденное) решение
асимптотически устойчивым?
Ответ: решение не будет асимптотически устойчиво, т.к. один
коэффициент характеристического уравнения равен нулю.
1.8.2.2 Критерий Рауса-Гурвица
Пусть дано характеристическое уравнение
0...)(
1
1
10
nn
nn
apapapapD
. (1.8.2.1)
Составим для него определитель Гурвица размера (n х n)
nn
n
aa
a
aa
aa
aaa
aaa
2
1
20
31
420
531
000
0000
000
000
00
00
. (1.8.2.2)
Следует обратить внимание на то, что в первой строке расположены
нечетные коэффициенты, во второй – четные, а на главной диагонали
y
y
y
tc,
y
y
y
y
t
0
t
0
43

расположены коэффициенты
nn
aaaa ,,...,,
121
.
В соответствии с критерием Рауса-Гурвица главные
диагональные миноры должны быть положительными, то есть
.0,0
,0,......,,0
11
3021
20
31
211
nnnnn
aa
aaaa
aa
aa
a
(1.8.2.3)
Критерий Рауса-Гурвица читается так.
Для того чтобы система была асимптотически устойчивой,
необходимо и достаточно, чтобы при
0
0
a
все главные
диагональные миноры (3) определителя Гурвица (2) были
положительны.
Из соотношений
0,0
11
nnnn
a
следует
0
n
a
.
Для систем первого и второго порядков критерий Рауса-Гурвица
сводится к условиям критерия о необходимых условиях устойчивости,
т.е. для этих систем необходимым и достаточным условием
асимптотической устойчивости является однознаковость всех
коэффициентов характеристического уравнения; если имеются
коэффициенты с противоположными знаками или нулевые, то система
будет неустойчивая.
Рассмотрим критерий Раусса-Гурвица для системы третьего
порядка с характеристическим уравнением
0)(
32
2
1
3
0
apapapapD
.
Определитель Гурвица и критерий Рауса-Гурвица имеют вид
.0,0,0,0;
0
0
0
30212310
31
20
31
aaaaaaa
aa
aa
aa
1.8.3 Частотные критерии устойчивости
Будем рассматривать следующие критерии:
— критерий Михайлова;
— критерий Найквиста;
— логарифмический критерий Найквиста.
1.8.3.1 Критерий Михайлова
Для его применения необходимо иметь характеристический
полином
y
y
y
tc,
y
y
y
y
t
0
t
0
44
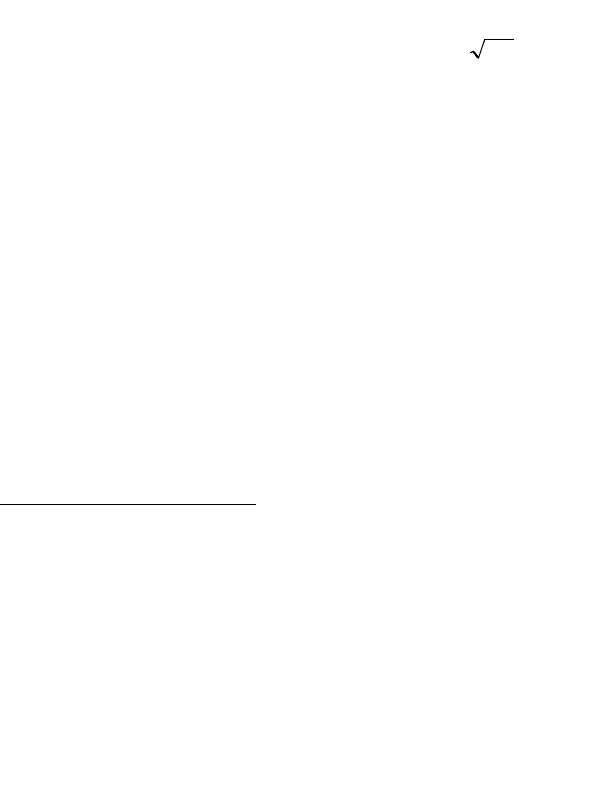
0...)(
1
1
10
nn
nn
apapapapD
. (1.8.3.1)
Подставим в (1) вместо
p
j
, где
1j
;
– частота,
которая меняется в диапазоне от 0 до ∞. В результате получим
комплексный полином
)()()(
jYXjD
, (1.8.3.2)
где
)(
X
– действительная часть, а
)(
Y
– коэффициент при
мнимой части.
...)(
6
6
4
4
2
2
nnnn
aaaaX
, (1.8.3.3)
...)(
7
7
5
5
3
31
nnnn
aaaaY
,
или
...)()(
6
7
4
5
2
31
nnnn
aaaaY
. (1.8.3.4)
Критерий Михайлова является графическим критерием. Для его
применения на комплексной плоскости строится годограф (траектория
конца вектора) Михайлова. На рис. 6 показаны годографы Михайлова
для систем различных порядков n, соответствующие асимптотической
устойчивости систем.
Для того чтобы система была асимптотически устойчивой,
необходимо и достаточно, чтобы при изменении частоты
от 0
до ∞ годограф Михайлова охватывал начало координат, проходя
последовательно столько квадрантов против часовой стрелки, каков
порядок системы (рисунок 6).
Если годограф Михайлова будет проходить через начало
координат, то система будет находиться на границе
устойчивости (рисунок 7).
Если годограф Михайлова не охватывает начало координат,
то САУ будет неустойчивой (рисунок 8).
Из критерия Михайлова вытекает критерий Эрмита-Билера. Как
следует из рисунка 6, при асимптотической устойчивости корни
полиномов
0)(,0)(
YX
чередуются.
y
y
y
tc,
y
y
y
y
t
0
t
0
45
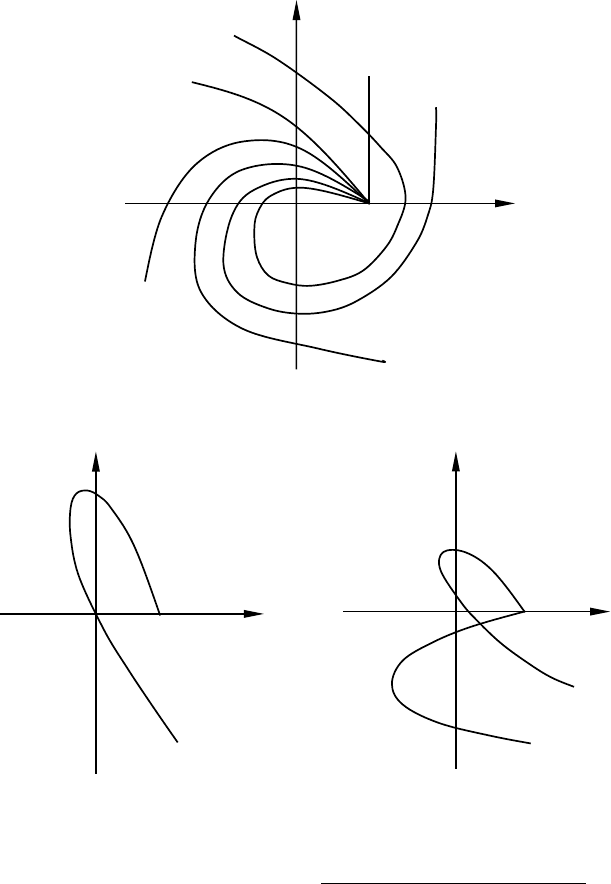
Рисунок 1.8.6 – Годографы Михайлова для устойчивых систем различных порядков
Рисунок 1.8.7
Рисунок 1.8.8
Критерий Эрмита-Билера. Для того чтобы система была
асимптотически устойчивой, необходимо и достаточно, чтобы
корни полиномов (3) и (4) были действительными положительными и
чередовались между собой, начиная с корня
0
для полинома (4).
Y(ω)
X(ω)
ω=0
n=1
n=5
n=4
n=3
n=2
n=6
Y(ω)
X(ω)
ω=0
Y(ω)
X(ω)
ω=0
y
y
y
tc,
y
y
y
y
t
0
t
0
46
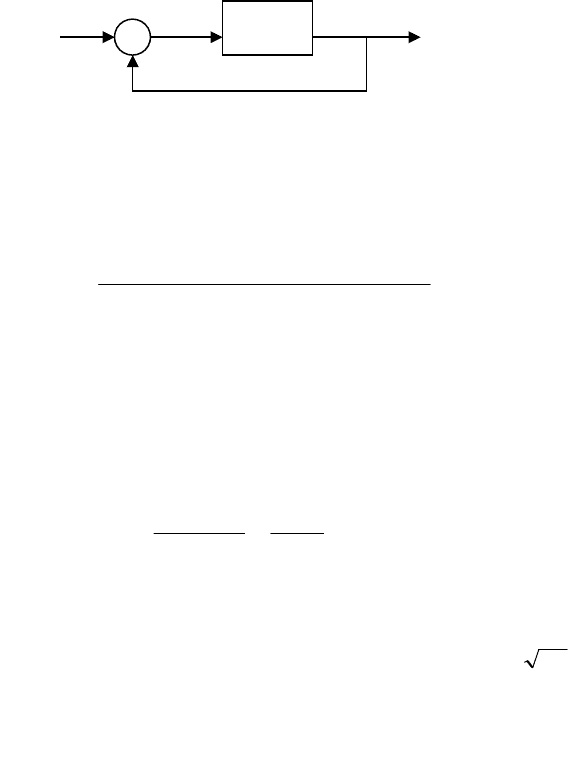
1.8.3.2 Критерий Найквиста
Этот критерий позволяет судить об устойчивости замкнутой
системы по АФЧХ разомкнутой системы. Для применения этого
критерия система приводится к виду с единичной обратной связью,
показанному на рис. 9.
Рисунок 1.8.9
На рис. 9
g
– задающее воздействие, равное желаемому
значению выходной переменной
y
;
x
– ошибка системы;
)( pW
–
передаточная функция разомкнутой системы, представленная в виде
)1...(
)1...(
)(
1
1
10
1
1
10
papapap
pbpbpb
kpW
q
qq
m
mm
. (1.8.3.5)
При таком представлении передаточной функции
k
–
коэффициент передачи разомкнутой цепи,
– степень астатизма.
При
0
система называется статической, при
...,2,1
система называется астатической первого, второго, … порядков.
Для реальных систем имеет место соотношение
mq
. (1.8.3.6)
Передаточная функция замкнутой САУ имеет вид
)(
)(
)(1
)(
pg
py
pW
pW
Ф
. (1.8.3.7)
Для получения характеристического уравнения надо
знаменатель приравнять нулю, то есть
0)(1 pW
. (1.8.3.8)
Подставим в уравнение (8)
jp
, где, как и ранее,
1j
,
– частота. Получим
1)(
jW
. (1.8.3.9)
Значение
j
, при котором выполняется условие (9), является корнем
характеристического уравнения (8), т.е.
jp
, что соответствует
границе устойчивости. Но
)(
jW
представляет собой АФЧХ
W(p)
g x
y
–
y
y
y
tc,
y
y
y
y
t
0
t
0
47
разомкнутой системы.
Таким образом, если АФЧХ разомкнутой системы при
изменении частоты от 0 до ∞ будет проходить через точку (-1; j0), то
система будет находиться на границе устойчивости.
Будем рассматривать две ситуации:
а) система в разомкнутом состоянии устойчива (асимптотически
устойчива или находится на границе устойчивости);
б) система в разомкнутом состоянии неустойчива.
Случай а):
Критерий Найквиста. Для того чтобы замкнутая система
была асимптотически устойчива, необходимо и достаточно,
чтобы при изменении частоты от 0 до бесконечности АФЧХ
разомкнутой системы не огибала точку с координатами (-1; j0).
Если АФЧХ будет проходить через эту точку, то замкнутая
САУ будет находиться на границе устойчивости.
Если АФЧХ будет огибать точку (-1; j0), то замкнутая САУ
будет неустойчивой.
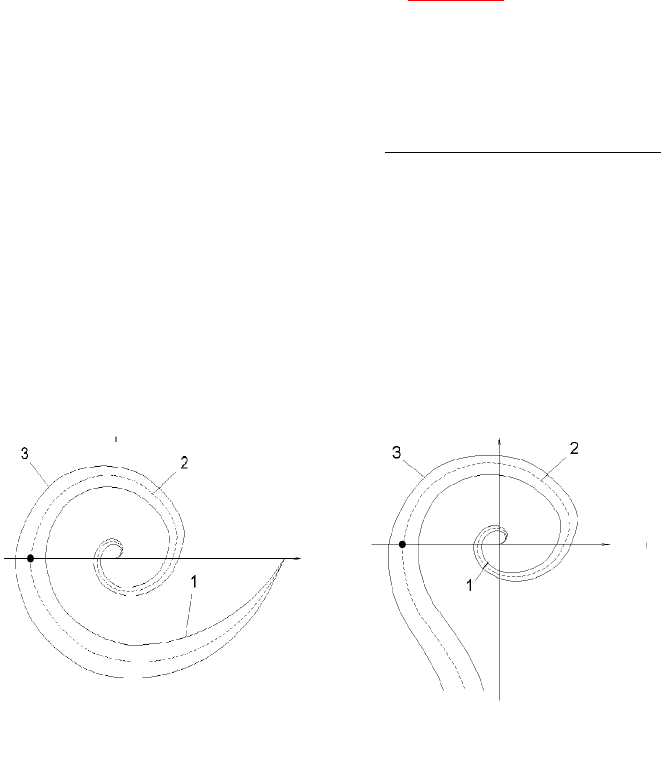
Годографы Найквиста для статической системы (
0
)
представлены на рис. 10, а для астатической системы (
1
) – на рис.
11.
Рисунок 1.8.10
Рисунок 1.8.11
На рисунках 10, 11:
)()()(
jVUjW
,
1 – асимптотически устойчивая замкнутая САУ,
-1
V(ω)
U(ω)
ω=0
a
n
-1
V(ω)
U(ω)
ω→
y
y
y
tc,
y
y
y
y
t
0
t
0
48
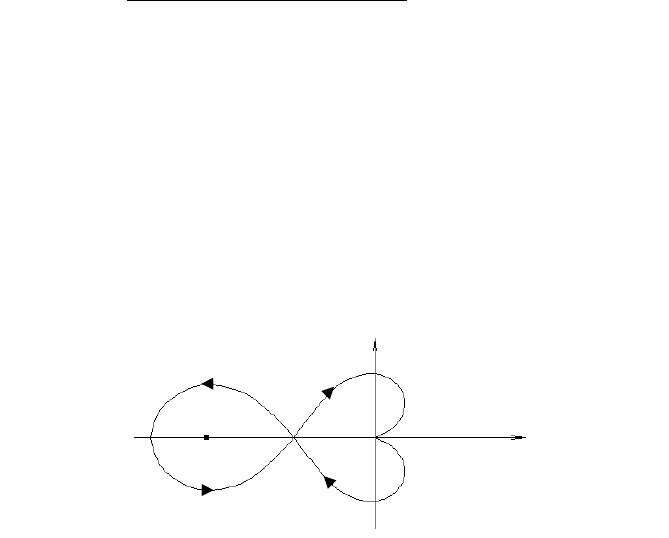
2 – гранично устойчивая САУ,
3 – неустойчивая САУ.
Случай б): система в разомкнутом состоянии неустойчива. Тогда
критерий Найквиста выглядит так:
Для того чтобы система, неустойчивая в разомкнутом
состоянии, была асимптотически устойчива в замкнутом
состоянии, необходимо и достаточно, чтобы при изменении
частоты от минус бесконечности до плюс бесконечности АФЧХ
разомкнутой системы охватывала точку с координатами (-1; j0)
столько раз, сколько корней в правой полуплоскости содержит
знаменатель передаточной функции разомкнутой системы. При
этом необходимо, чтобы при изменении частоты от минус
бесконечности до плюс бесконечности конец вектора
)(
jW
поворачивался вокруг точки (-1; j0) против часовой стрелки на угол
2m
, где
m
– количество неустойчивых корней в знаменателе
передаточной функции разомкнутой системы.
При
1m
(одном неустойчивом корне) годограф Найквиста
представлен на рисунке 12.
Рисунок 1.8.12
1.8.3.3 Применение критерия Найквиста к системам с
чистым запаздыванием
Рассмотрим структурную схему САУ, представленную на рис.
13,
V(ω)
U(ω)
ω=0
0
-1
ω→
ω→-
y
y
y
tc,
y
y
y
y
t
0
t
0
49
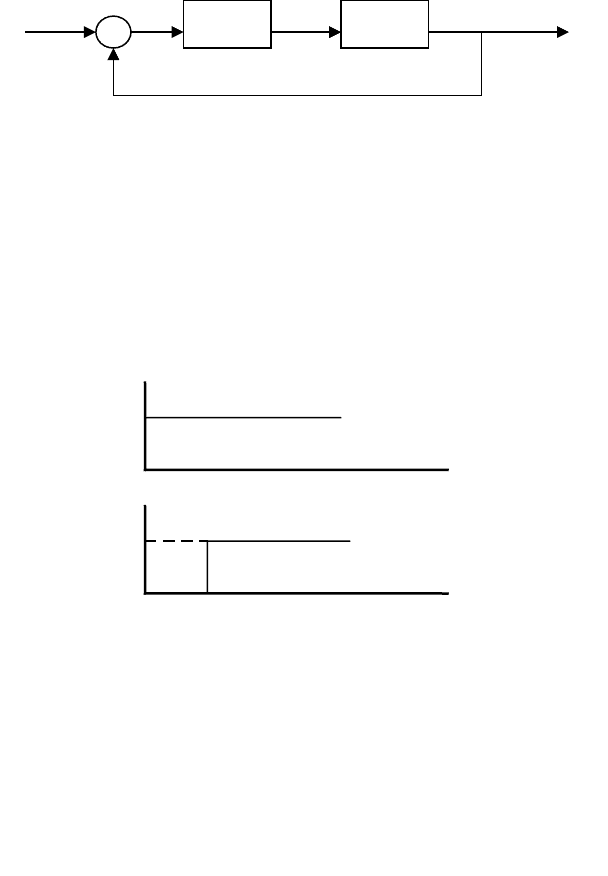
Рисунок 1.8.13
где
)(
1
pW
– передаточная функция разомкнутой системы без учёта
чистого запаздывания;
p
epW
)(
2
– передаточная функция чистого запаздывания (
– величина чистого запаздывания).
На рис. 14 продемонстрировано соотношение между входным (
u
) и выходным
)( y
сигналами звена чистого запаздывания.
Рисунок 1.8.14
Пусть система без учёта чистого запаздывания является
асимптотически устойчивой с годографом Найквиста,
представленным на рис. 15.
Задача: найти значение чистого запаздывания, при котором
система выходит на границу устойчивости. Это значение называется
критическим запаздыванием
кр
.
Передаточная функция разомкнутой САУ
)()()(
21
pWpWpW
,
W
1
(p) W
2
(p)
g x
u y
–
t
t
1
1
u
y
0
0
y
y
y
tc,
y
y
y
y
t
0
t
0
50
