Потапенко Е.М., Казурова А.Е. Основы теории автоматического управления
Подождите немного. Документ загружается.

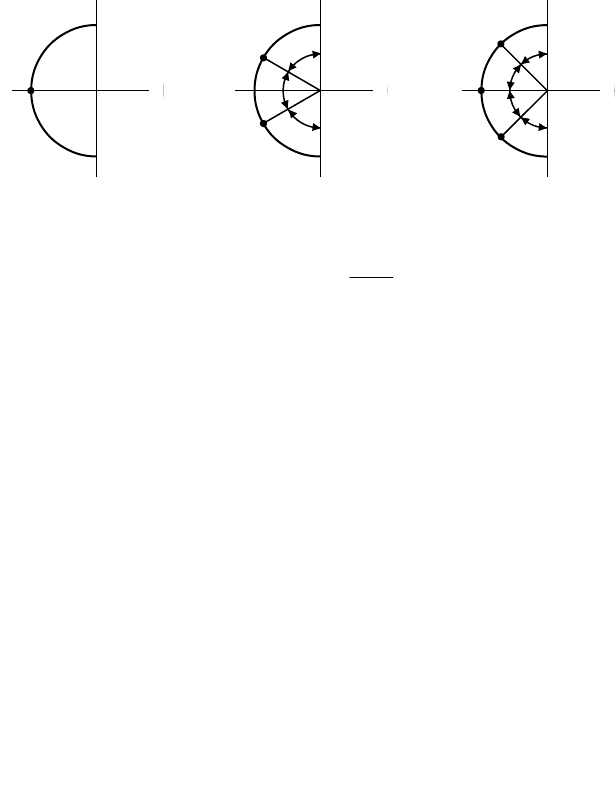
Рисунок 4.1.3 Рисунок 4.1.4 Рисунок 4.1.5
п
п
t
t
5,12
5,12
00
.
Таким образом, становится известным желаемое
характеристическое уравнение. Синтез САУ с помощью модального
управления осуществляется следующим образом:
1) составляется характеристическое уравнение системы, в
котором неизвестные параметры заданы буквенно;
2) по графику определяется
0
;
3) полученное характеристическое уравнение системы
сравнивается со стандартным уравнением того же порядка, в
результате чего получается система уравнений относительно
неизвестных параметров системы;
4) находятся неизвестные параметры.
4.2 Запись дифференциальных уравнений в пространстве
состояний
Пусть задано уравнение
bfxaxax
n
nn
...
)1(
1
)(
, (4.2.1)
где
x
– выходной сигнал,
f
– входной сигнал.
Представим это уравнение в виде системы дифференциальных
уравнений первого порядка, разрешённых относительно производных
(Форма Коши). В данном случае для уравнения (1) существует
бесконечное количество представлений в пространстве состояний. Всё
зависит от выбора вектора состояния системы. В качестве координат
вектора состояния системы выберем следующие координаты:
Re
Im
p
1
–ω
0
Im
–ω
0
p
1
p
2
Re
Im
–ω
0
p
1
p
2
Re
p
3
133

n
n
zxzxzx
)1(
21
,...,,
. (4.2.2)
Согласно (1) и (2), вновь введенные переменные подчиняются системе
уравнений
....
,,,...,,
1121
1123221
bfzazazaz
zzzzzzzz
nnnn
nnnn
(4.2.3)
Представим эту систему в векторно-матричном виде, введя
обозначения
.
0
0
,
...
1...000
...............
0...100
0...010
,
121
2
1
b
B
aaaa
A
z
z
z
z
nnn
n
(4.2.4)
С учетом обозначений (4) система уравнений (3), а, следовательно, и
уравнение (1) представляются в виде
BfAzz
. (4.2.5)
Запись в виде (4) и (5) называется представлением уравнения (1) в
пространстве состояний. Вектор
z
называется вектором
состояния.
Рассмотрим систему дифференциальных уравнений,
описывающих систему управления
,......
...............................................................................
,......
22112211
121211112121111
mmnnnnnnnnn
mmnn
ubububxaxaxax
ubububxaxaxax
(4.2.6)
где
n
xxx ,...,,
21
– выходные переменные;
),1;,1(),,1,(
,,
mjnibnjia
jiji
– коэффициенты;
),1( miu
i
– входные переменные (управляющие воздействия).
Если считать, что
n
xxx ,...,,
21
полностью определяют состояние
системы, то в качестве вектора состояния можно выбрать вектор
T
n
xxxx ],...,,[
21
.
Представим систему (6) в векторно-матричном виде, введя
обозначения
134
mnmn
m
nnn
n
n
u
u
u
bb
bb
B
aa
aa
A
x
x
x
1
1
111
1
1111
,
...
.........
...
,
...
.........
...
,
.
BuAxx
.
4.3 Описание работы двигателя постоянного тока (ДПТ)
независимого возбуждения (НВ) в пространстве состояний
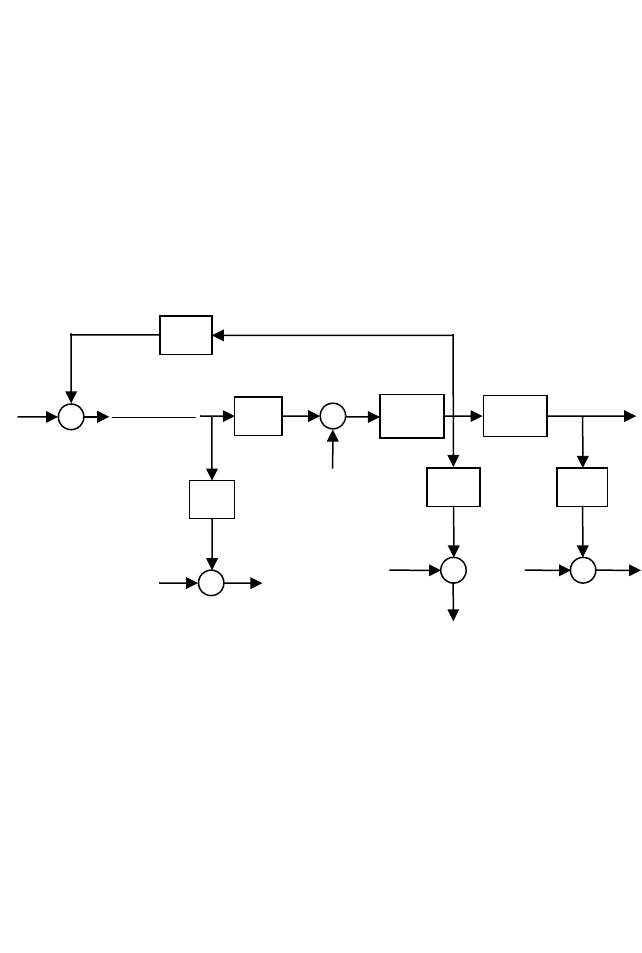
Структурная схема ДПТ представлена на рис. 1.
Рисунок 4.3.1 – Структурная схема работы ДПТ НВ
На рис. 1
д
u
– напряжение, прикладываемое к якорной цепи
двигателя;
e
– ЭДС двигателя;
д
M
– электромагнитный момент двигателя;
н
M
– момент нагрузки;
I
– момент инерции ротора;
– угловая скорость ротора;
– угол поворота ротора;
uuu
i
,,
– выходные сигналы измерительных
C
m
K
i
1/Ip
1/p
K
K
C
e
u
д
e
M
д
M
M
н
u
i
'
u
i
w
i
w
w
u
u
'
u
–
–
u
'
1
1
pT
R
я
я
u'
i
135
датчиков, соответственно, тока, угловой скорости, угла поворота;
www
i
,,
– погрешности измерения;
kkk
i
,,
– коэффициенты передачи датчиков;
i
– ток якоря;
яя
TR ,
– сопротивление и постоянная времени якорной
цепи;
me
CC ,
– коэффициенты ЭДС и электромагнитного
момента (в системе единиц СИ
me
CC
);
p
– оператор дифференцирования.
Запишем систему уравнений, соответствующую рис. 1. Имеют
место соотношения
,
,
,
1
нmнд
яя
eд
MiCMMM
uRiiT
Cuu
(4.3.1)
с учетом которых
))((
1
1
eдя
я
CuRi
T
i
, (4.3.2)
)(
11
нm
MiC
I
M
I
, (4.3.3)
. (4.3.4)
На ДПТ воздействуют два внешних воздействия:
д
u
и
н
M
.
Представим систему уравнений (2)-(4) в векторно-матричном виде.
Введём в рассмотрение вектор состояния и матрицы
136

.
0
0
,
0
0
1
,
010
00
0
1
,
1
3
2
1
IG
RT
B
I
C
RT
C
T
A
i
x
x
x
x
яя
m
яя
e
я
(4.3.5)
С учетом обозначений (5) система (2)-(4) перепишется в виде
.
нд
GMBuAxx
(4.3.6)
В соответствии с рис. 1 введём в рассмотрение вектор
измерения
,·
00
00
00
w
i
C
ii
w
w
wi
k
k
k
u
u
u
y
(4.3.7)
где
C
– матрица измерения,
w
– вектор погрешностей измерения.
Тогда уравнение (7) можно представить в векторно-матричном виде
.wCxy
(4.3.8)
В случае измерения только
u
матрица
C
будет состоять
только из третьей строки. При измерении
i
u
и
u
в матрицу
C
не
будет входить вторая строка.
4.4 Модальное управление в пространстве состояний
Рассмотрим систему
,BuAxx
(4.4.1)
,Cxy
(4.4.2)
где
n
Rx
– вектор состояния системы,
m
Ru
– вектор управления,
r
Ry
– вектор измерения,
137

nn
RA
– матрица объекта управления,
mn
RB
– матрица управления,
nr
RC
– матрица измерений.
Закон управления (регулятор) представим в виде
PCxPyu
, (4.4.3)
где
rm
RP
– матрица коэффициентов закона управления.
Подставим (3) в (1). Тогда
.)( xBPCAx
(4.4.4)
Запишем уравнение (4) в операторном виде, получим
0)( xBPCAEp
. (4.4.5)
Если бы определитель матрицы в скобках не был равен 0, то из
уравнения (5) следовало бы
0x
. Этот случай не имеет физической
сути, т.к. в переходных процессах
0x
. Для того чтобы уравнение
(5) давало нетривиальное решение, определитель матрицы в скобках
должен равняться 0.
0)det( BPCAEp
. (4.4.6)
Левая часть уравнения (6) называется характеристическим
определителем для уравнения (4). Раскрыв определитель в (6),
получим характеристическое уравнение.
Уравнение (4) должно быть асимптотически устойчивым.
Поэтому для асимптотической устойчивости можно воспользоваться
любым критерием устойчивости, с помощью которого выбирается
матрица
P
, элементами которой являются коэффициенты закона
управления. Для того чтобы обеспечить заданный переходный
процесс, удобно воспользоваться модальным управлением,
рассмотренным в подразделе 4.1, с помощью которого выбираются
коэффициенты закона управления. Однако это можно сделать не
всегда. Это можно сделать только в том случае, когда система (1)
является полностью управляемой. Когда это так, то пара матриц (
BA,
) называется полностью управляемой.
Полная управляемость означает, что существует управляющее
воздействие
u
, переводящее объект из любого начального состояния
0
x
в любое наперёд заданное
k
x
.
Условием полной управляемости является равенство ранга
матрицы управляемости порядку системы
n
.
138

.],...,,,[
12 nmnn
y
RBABAABBQ
(4.4.7)
4.5 Динамические фильтры
Изложенный в предыдущем разделе метод расположения
корней характеристического уравнения предполагает, что все
элементы вектора состояния измеряются (матрица
C
должна быть
диагональной). На практике обычно можно измерить только часть
элементов вектора состояния, например, для управления рукой робота
надо знать угловые перемещения в суставах робота и их скорости;
скорости обычно замерить труднее, чем перемещения. Кроме того, на
руке робота стараются устанавливать как можно меньше элементов
системы управления. Поэтому обычно датчики скорости стараются не
устанавливать и надо осуществить управление только с помощью
датчиков перемещения.
Пусть объект управления описывается системой
GfBuAxx
, (4.5.1)
DvCxy
, (4.5.2)
где
f
– вектор внешних воздействий на объект,
G
– матрица внешних воздействий,
v
– вектор погрешностей датчиков,
D
– матрица вектора погрешностей.
Размерности вновь введенных векторов и матриц даны в (3).
qrlnqlrmn
RDRGRvRfRyRuRx
;;;;;;
.
(4.5.3)
Составим структурную схему объекта управления,
соответствующую системе (1), (2) и изображенную в верхней части
рис. 1.
139
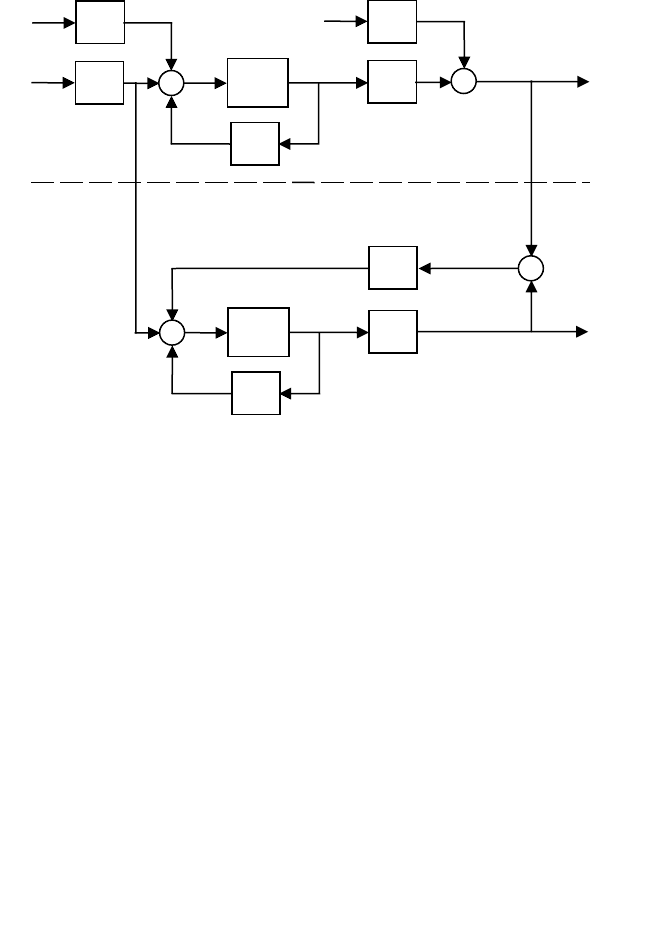
Рисунок 4.5.1 – Структурные схемы объекта управления и динамического фильтра
В отличие от материально существующего объекта управления
(например, электродвигателя с технологическими механизмами),
динамический фильтр программируется и решается в вычислителе.
Структурная схема динамического фильтра должна в максимально
возможной степени совпадать со структурной схемой объекта
управления (нижняя часть рис. 1). В структурную схему фильтра не
вошли цепи, связанные с неизвестными входными воздействиями
f
и
v
. Для синхронизации работы динамического фильтра с работой
объекта управления предназначена цепь, содержащая матрицу
L
коэффициентов усиления фильтра размером (
rn
). По структурной
схеме фильтра запишем уравнение его работы.
)
ˆ
(
ˆˆ
yyLBuxAx
. (4.5.4)
Разность
yy
ˆ
называется невязкой. С помощью уравнения (2)
представим уравнение (4) в виде
LDvxxLCBuxAx )
ˆ
(
ˆˆ
. (4.5.5)
Введём в рассмотрение ошибку динамического фильтра
xxx
ˆ
~
. (4.5.6)
f
G
D
1/p
B
u
C
A
v
x
–
L
объект управления
динамический фильтр
x
1/p
C
A
x
ˆ
x
ˆ
yy
ˆ
y
ˆ
y
140

Для получения динамического уравнения ошибки фильтра
вычтем из уравнения (5) уравнение (1), получим
GfLDvxLCxAx
~~~
. (4.5.7)
Уравнение (7) можно рассматривать как неоднородное
дифференциальное уравнение с внешним воздействием
GfLDv
.
Для того чтобы ошибка фильтра была ограниченной, необходимо,
чтобы частное решение уравнения (7) было асимптотически
устойчивым. Для этого необходимо и достаточно, чтобы нулевое
решение уравнения (8) было асимптотически устойчивым.
xLCAx
~
)(
~
. (4.5.8)
Для уравнения (8) характеристическое уравнение будет иметь
вид
0)det( LCAEp
, (4.5.9)
где
L
– неизвестная матрица коэффициентов усиления
динамического фильтра. Раскрывая определитель и приравнивая
полученное к какому-либо стандартному полиному, можно записать
систему алгебраических уравнений для нахождения элементов
матрицы
L
. При этом переходный процесс уравнения (8) будет
соответствовать заданному. В том случае, когда решение уравнения
(8) стремится к 0, из (6) следует, что
xx
t
ˆ
lim
. (4.5.10)
Соотношение (10) справедливо только для уравнения (8). В случае
уравнения (7)
x
ˆ
будет стремиться не к
x
, а к некоторой окрестности
(трубке) вектора
x
. Диаметр этой трубки обусловлен внешним
воздействием уравнения (7). В случае, когда этот диаметр мал, вектор
x
ˆ
на практике можно отождествлять с вектором
x
и использовать
x
ˆ
при формировании закона управления.
Уравнение (7) представляет собой матричное инерционное
звено. Известно, что инерционное звено является хорошим фильтром
низких частот (отфильтровывает высокочастотные помехи),
следовательно, частное решение уравнения (7) будет иметь
существенно уменьшенные высокочастотные помехи, т.е.
динамический фильтр, помимо восстановления (оценки) всего вектора
состояния объекта управления, будет также отфильтровывать
высокочастотные погрешности датчиков и высокочастотные внешние
воздействия на объект. В том случае, когда матрица
L
выбрана так,
141
что
x
ˆ
является наилучшей среднеквадратической оценкой вектора
состояния объекта
x
, динамический фильтр называется фильтром
Калмана. В том случае, когда матрица
L
выбирается из других
соображений, динамический фильтр называется наблюдателем
Льюэнбергера.
Динамические фильтры позволяют восстановить весь вектор
состояния и отфильтровать высокочастотные воздействия на объект и
погрешности датчика. Однако не для каждой системы можно
построить динамический фильтр. Для того чтобы можно было
построить динамический фильтр, система должна быть полностью
наблюдаемой (говорят, что пара матриц (
CA,
) должна быть
полностью наблюдаемой).
Система называется полностью наблюдаемой, когда её вектор
состояния можно восстановить за сколь угодно малый промежуток
времени.
Теорема 1. Система является полностью наблюдаемой тогда и
только тогда, когда матрица наблюдаемости
н
Q
имеет ранг,
равный порядку системы
n
, где
n
– размерность вектора
состояния системы (
n
Rx
).
.])(,...,)(,,[
12 nnrTnTTTTTT
н
RCACACACQ
(4.5.11)
Ранг матрицы
н
Q
равен
n
тогда и только тогда, когда из её блоков
можно составить матрицу
nn
, определитель которой не равен 0.
Существует и другой, более удобный критерий полной
наблюдаемости.
Теорема 2. Система (1), (2) является полностью наблюдаемой
тогда и только тогда, когда при
0,0,0,0 yufv
из
системы (1), (2) следует
0x
. Для применения этой теоремы
удобнее, когда система (1), (2) представлена в скалярном виде, т.е. в
виде системы дифференциальных уравнений, причём не обязательно в
форме Коши.
Пример. Исследовать наблюдаемость двигателя постоянного
тока при измерении только угла
.
Уравнения исследуемой системы имеют вид
eяя
CuRiiT
1
, (4.5.12)
1
)(
IMiC
нm
, (4.5.13)
142
