Потапенко Е.М., Казурова А.Е. Основы теории автоматического управления

Подождите немного. Документ загружается.

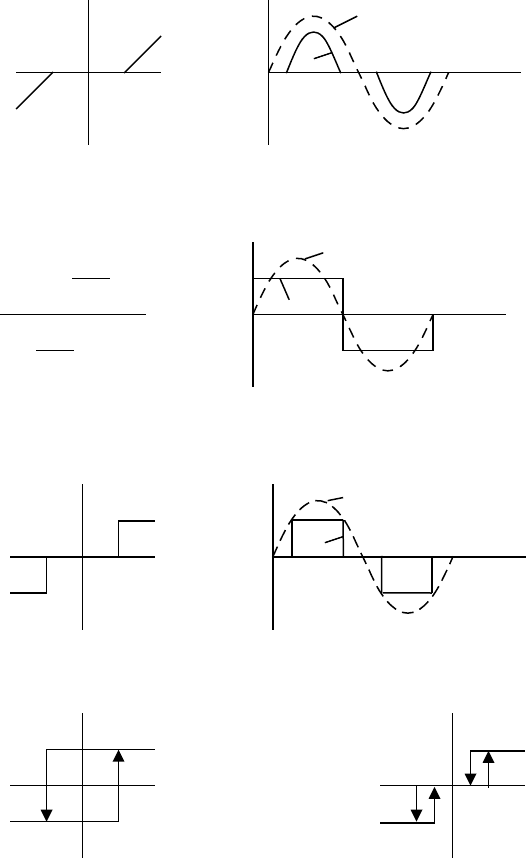
Рисунок 3.1.2 – Звено с зоной нечувствительности

Рисунок 3.1.3 – Идеальное двухпозиционное реле (кулоново трение)

Рисунок 3.1.4 – Идеальное трёхпозиционное реле

Рисунок 3.1.5 – Двухпозиционное

реле с гистерезисом

Рисунок 3.1.6 – Трехпозиционное реле

с гистерезисом

x,y

тр

= -k sign x

x,y



tc,





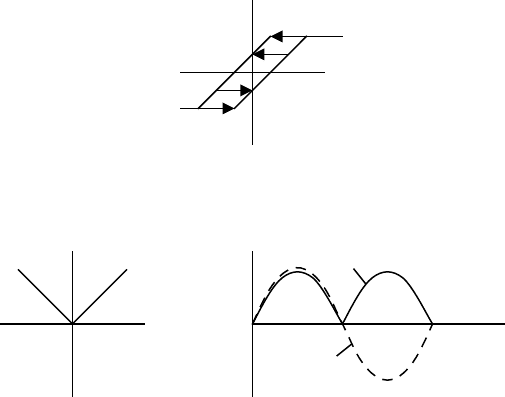
Рисунок 3.1.7 – Петля гистерезиса (звено с мёртвым ходом)

Рисунок 3.1.8 – Звено выделения модуля

Хотя нелинейности и затрудняют исследование САУ, они часто

специально вводятся в систему управления, например, для

компенсации уже существующих в системе управления

нежелательных нелинейностей. Кроме того, оптимальные по

быстродействию САУ всегда являются нелинейными.

3.2 Структурные преобразования САУ

Нелинейности существенно усложняют исследования САУ.

Нельзя переносить звено со входа нелинейного звена на его выход и

обратно. Однако если на входе или на выходе нелинейного звена

имеются линейные цепи, то в пределах этих цепей можно

осуществлять преобразования по правилам линейных цепей.

Статические характеристики нелинейных систем.

Последовательное соединение звеньев.

Рассмотрим три последовательно соединенных звена (рис. 1).

x,y



tc,





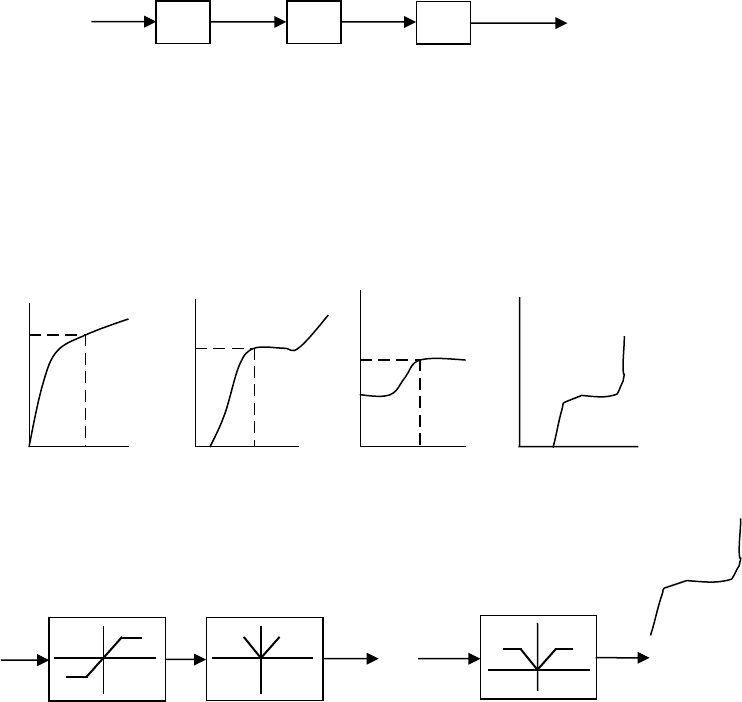
Рисунок 3.2.1 – Последовательное соединение нелинейных звеньев

Задача: зная статические характеристики отдельных звеньев,

определить статическую характеристику всей цепи. На рис. 2

изображены статические характеристики трёх звеньев,

представленных на рис. 1, и последовательность нахождения

выходного сигнала

yy 

по входному сигналу

xx 

Рисунок 3.2.2 – Получение суммарной статической характеристики

Пример. Найти статическую характеристику цепи (рис. 3).

Рисунок 3.2.3 – а) статические характеристики звеньев, б) результирующая

статическая характеристика цепи

Параллельное соединение звеньев.

Задача: по статическим характеристикам отдельных звеньев

найти эквивалентную статическую характеристику всей цепи (рис. 4).

x=x

' x

а)

б)



tc,





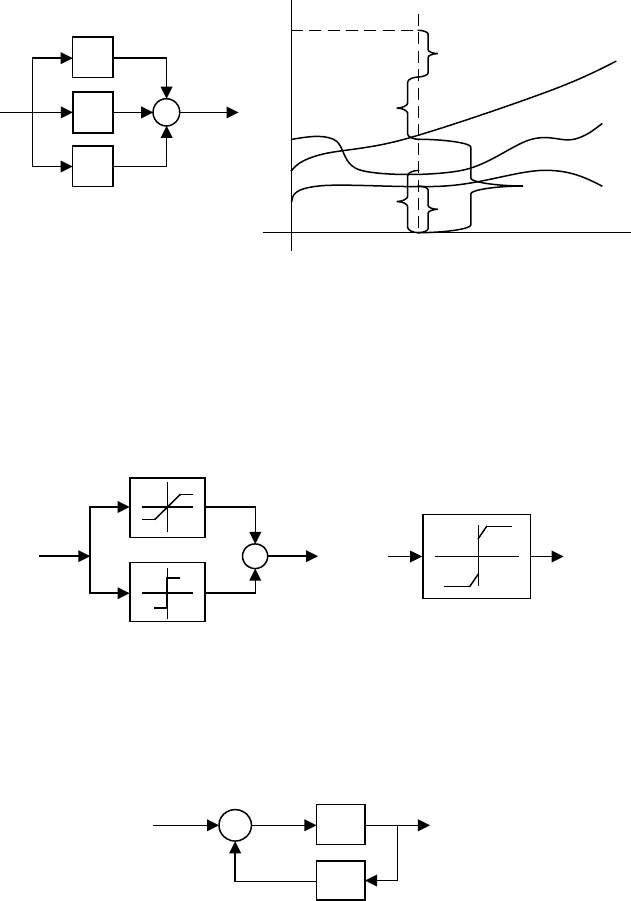
Рисунок 3.2.4 – а) параллельное соединение нелинейных звеньев, б)

последовательность получения результирующей статической характеристики

Пример. Найти статическую характеристику цепи. На рис. 5а

дано параллельное соединение двух звеньев, на рис. 5б –

эквивалентное звено и его статическая характеристика.

Рисунок 3.2.5 – а) параллельное соединение звеньев и их статические характеристики,

б) эквивалентная статическая характеристика одного звена

Встречно-параллельное соединение звеньев (рис. 6).

Рисунок 3.2.6 – Встречно-параллельное соединение нелинейных звеньев

=х

+у

=у

а)

б)

а)

б)



tc,





yxx 

, (3.2.1)

Порядок построения эквивалентной схемы:

1. Задается значение

2. По статической характеристике звена 1 находим

yxy 

3. По статической характеристике звена 2 находим

4. По зависимости (1) находим

5. Поскольку

известны, то можно определить всю

статическую характеристику.

3.3 Понятие о фазовом пространстве и фазовых траекториях

Состояние САУ определяется рядом координат. Например,

систему

3210

 yayayaya



, (3.3.1)

где

– коэффициенты, можно определить

координатами

yx 









. (3.3.2)

Систему уравнений

zcybxaz

zcybxay

zcybxax

333

222

111





(3.3.3)

можно определить координатами

zqyqxq 

321

. (3.3.4)

Минимальное количество координат, полностью определяющих

состояние системы, равно порядку системы. Вектор (матрица-

столбец или матрица-строка), составленный из координат системы,

полностью определяющих её состояние, называется вектором

состояния системы.

Например, для системы (1) вектор состояния

xxxx )(

321



для системы (3) вектор состояния

qqqq )(

321



При рассмотрении САУ широко используется понятие фазовых

пространств.

Фазовое пространство – это пространство в прямоугольной

системе координат, осями которой являются элементы вектора



tc,





состояния.

Для системы второго порядка это фазовая плоскость. Для

системы третьего порядка это трёхмерное фазовое пространство и

т.д. Состоянию системы в каждый момент времени соответствует

определённая точка в фазовом пространстве. Эта точка называется

изображающей точкой. При изменении состояния системы

изображающая точка перемещается, описывая траекторию, которая

называется фазовой траекторией. Для временной привязки процесса

в отдельных точках фазовой траектории проставляется время,

которому эта точка соответствует.

Рассмотрим построение фазовых траекторий системы второго

порядка

 yydTyT



где

– постоянная времени,

– параметр затухания. При 1)

0d

система гранично устойчива, 2)

0d

система асимптотически

устойчива, 3)

0d

система неустойчива. На рис. 1а представлены

процессы изменения координаты (переменной)

, на рис. 1б –

скорости



изменения координаты

для трёх указанных случаев,

на рис. 1в – фазовый портрет, построенный по указанным

переменным.

Для построения фазовых траекторий, соответствующих трём

переходным процессам, представленным на рис. 1, надо для ряда

моментов времени по рис. 1а, 1б определить значения



и для

каждого момента на рис. 1в построить точку. Соединив эти точки,

получим соответствующие фазовые траектории. На рис. 1в

стрелками показаны направления движения изображающих точек.

Направление движения изображающей точки можно определить

непосредственно по рис. 1в следующим образом. В верхней (нижней)

полуплоскости

)0(0  yy



, где



– скорость изменения

. При

)0(0  yy



будет возрастать (уменьшаться). Это означает, что

при данном на рис. 1в расположении осей фазовые траектории будут

развиваться по часовой стрелке. Следует заметить, что, если поменять

оси



местами, изображающая точка будет двигаться



tc,





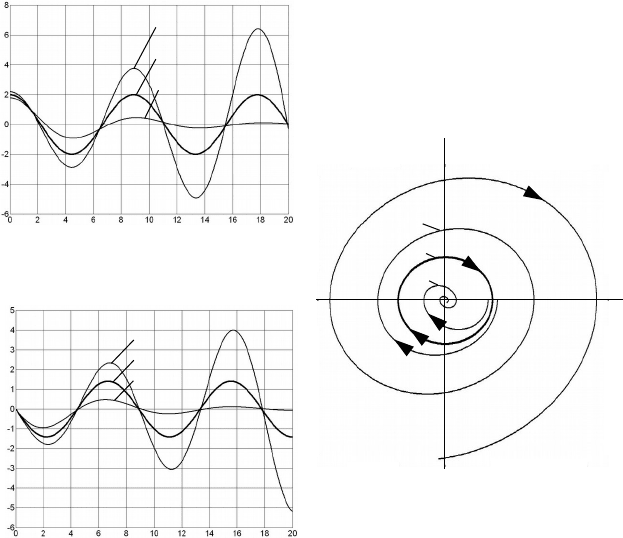
Рисунок 3.3.1

против часовой стрелки. Как видно на рис. 1в, при асимптотической

устойчивости (неустойчивости) изображающая точка будет

стремиться к нулю (от нуля). При граничной устойчивости фазовая

траектория будет замкнутой кривой 1. При колебательных процессах

фазовые траектории имеют вид спиралей.

3.4 Особенности динамики нелинейных систем

У линейных систем устойчивость и качество переходных

процессов не зависят ни от величины внешних воздействий, ни от

начальных условий. В нелинейных системах процесс гораздо сложнее.

В зависимости от начальных условий система может оказаться как

c, t

а)

c, t



б)



в)

tc,





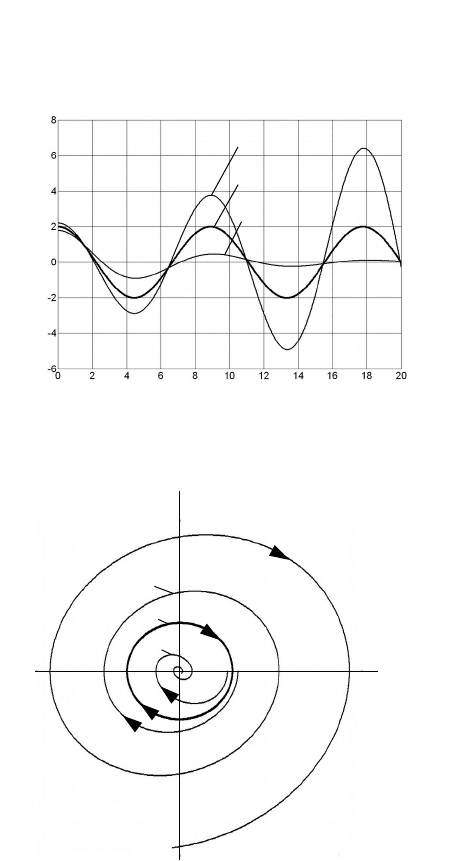
устойчивой, так и неустойчивой. На рис. 1 между начальными

условиями

существует начальное условие

, при

котором процесс гранично устойчив. На рисунке 2 представлены

фазовые траектории для тех же процессов, что и на рисунке 1.

Рисунок 3.4.1

Рисунок 3.4.2

Замкнутая траектория 1 на рис. 2 называется предельным циклом.

tc,





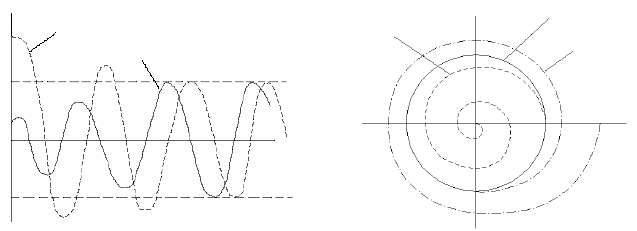
Возможен и другой случай, представленный на рис. 3, когда при

больших начальных условиях колебания уменьшаются, а при малых –

система неустойчива (колебания возрастают). На рис. 4 изображены

фазовые траектории для тех же процессов, что и на рис. 3. Процессы 2

и 3 стремятся к предельному циклу 1.

Рисунок 3.4.3 – Устойчивый

предельный цикл (автоколебания)

Рисунок 3.4.4 – Фазовые портреты

процессов, показанных на рис. 3

На рисунках 2 и 4 между траекториями 2 и 3 существуют

замкнутые траектории 1, которые называются предельными

циклами.

Предельные циклы могут быть устойчивыми, неустойчивыми и

полуустойчивыми. Если все фазовые траектории приближаются к

предельному циклу как изнутри, так и снаружи, то такой предельный

цикл называется устойчивым (рис. 4). В этом случае в системе

возникают автоколебания.

Если все фазовые траектории отходят от предельного цикла как

снаружи, так и изнутри его, то такой предельный цикл называется

неустойчивым (рис. 2).

Если фазовые траектории с одной стороны отходят от

предельного цикла, а с другой стороны подходят к нему, то такой

предельный цикл называется полуустойчивым. Колебания в системе,

соответствующие устойчивому предельному циклу, называются

автоколебаниями.

Следует обратить внимание на то, что автоколебания

поддерживаются самой системой, даже без внешних воздействий.

На рисунке 2 траектория 1 соответствует асимптотической





устойчивости начала координат «0».

Асимптотическая устойчивость будет иметь место только в том

случае, когда начальные условия взяты в ограниченной окрестности

начала координат, если же начальные условия выбрать вне этой

окрестности, то начало координат «0» окажется неустойчивым.

В связи с этим в нелинейных системах различают

асимптотическую устойчивость в малом, в большом и в целом

(глобальная асимптотическая устойчивость).

Если асимптотическая устойчивость начала координат имеет

место при бесконечно малых отклонениях от начала координат, то

будет асимптотическая устойчивость в малом.

Если асимптотическая устойчивость будет иметь место при

конечных отклонениях от начала координат, то будет

асимптотическая устойчивость в большом.

Если асимптотическая устойчивость будет иметь место при

любых начальных отклонениях от начала координат, то говорят, что

начало координат является асимптотически устойчивым в целом.

Асимптотически устойчивая линейная система всегда является

асимптотически устойчивой в целом или глобально асимптотически

устойчивой.

Практической устойчивостью начала координат называется

такая ситуация, когда начало координат является неустойчивым в

малом, а предельный цикл, содержащий начало координат, является

устойчивым по отношению к наружным траекториям, причём

величина предельного цикла позволяет системе успешно

функционировать.

3.5 Исследование устойчивости методами Ляпунова

Методы исследования устойчивости Ляпунова позволяют

исследовать устойчивость систем управления, описываемых

линейными, нелинейными, дискретными, непрерывными,

бесконечномерными уравнениями, а также уравнениями в частных

производных.

Достоинство этого метода заключается в том, что для

исследования устойчивости не требуется находить ни решения

дифференциальных уравнений, ни рассчитывать корни.

Физическая суть методов Ляпунова. На рисунке 1 представлена

