Потапенко Е.М., Казурова А.Е. Основы теории автоматического управления
Подождите немного. Документ загружается.

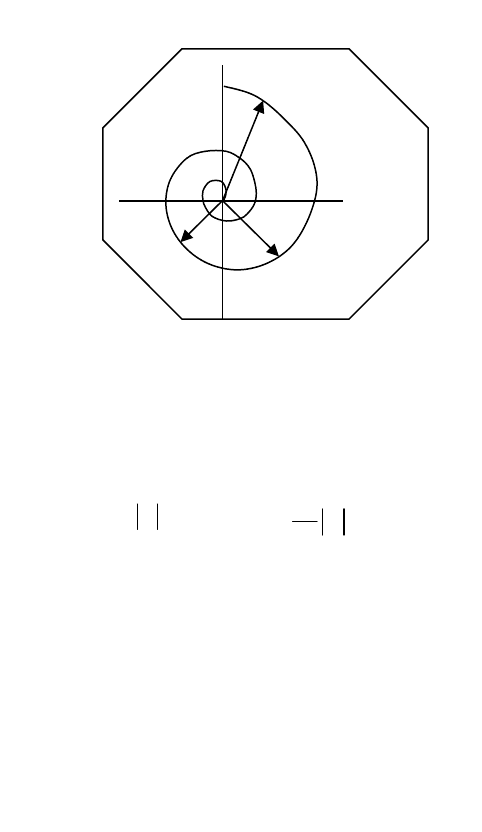
фазовая траектория асимптотически устойчивой САУ. Стрелками
указаны различные положения радиус-вектора
.
Рисунок 3.5.1 – Фазовый портрет асимптотически устойчивой траектории
Радиус-вектор изображающей точки на рис. 1 определяется
выражением
2
2
2
1
2
xx
.
Условием асимптотической устойчивости являются условия
0lim
t
, или
0
dt
d
.
Для системы третьего порядка
2
3
2
2
2
1
2
xxx
.
Для системы n-го порядка
22
2
2
1
2
...
n
xxx
.
Помимо перечисленных функций об асимптотической
устойчивости можно судить и по другим функциям, например, для
системы 2-го порядка
00lim0,
21
2
22
2
11
VVaaxaxaV
t
.
Или другая четная функция
4
22
2
11
xaxaV
.
Функция
V
, с помощью которой удаётся судить об
устойчивости системы, называется функцией Ляпунова.
Для функции Ляпунова характерно то, что она является всегда
положительной и обращается в 0 только в начале координат.
yx
2
yx
1
D
ρ
t
0
t
0
93

Функция
),...,,(
21 n
xxxV
, зависящая от всех координат
вектора состояния, называется определённо положительной
(отрицательной) в области
D
, содержащей начало координат, если
в этой области она везде положительна (отрицательна) кроме начала
координат
0...
321
n
xxxx
, где она обращается в ноль.
Функция
),...,,(
21 n
xxxV
называется знакоположительной
(знакоотрицательной), если она в этой области удовлетворяет
соотношению
)0(0 VV
.
Признаками асимптотической устойчивости системы являются:
существование для исследуемых уравнений определённо
положительной функции
V
и в любой момент времени
0V
, т.е.
V
должна быть определённо отрицательной.
3.5.1 Теорема Ляпунова об асимптотической устойчивости
Рассмотрим систему нелинейных дифференциальных уравнений
nixxxXx
nii
,1),...,,(
21
. (3.5.1.1)
i
X
– в общем случае нелинейные функции.
Теорема Ляпунова. Если для системы (1) в области
D
,
содержащей начало координат, существует определённо
положительная функция
V
, полная производная которой по времени
V
, взятая в силу системы (1), будет определённо отрицательной,
то начало координат будет асимптотически устойчивым при
условии, что начальные условия взяты из области
D
.
Пусть для системы (1) существует функция Ляпунова
),...,,(
21 n
xxxV
. (3.5.1.2)
Фраза “полная производная по времени, взятая в силу системы (1)”
означает следующее:
n
i
i
i
n
i
i
i
X
x
V
x
x
V
V
11
)1(
(...)
. (3.5.1.3)
Пример. Пусть дана система нелинейных уравнений
.
,
3
212
2
3
11
dxcxx
bxaxx
(3.5.1.4)
Выберем в качестве функции Ляпунова функцию
2
2
2
1
bxcxV
, (3.5.1.5)
где
t
0
t
0
94

0, bc
. (3.5.1.6)
В соответствии с (3) получим полную производную по времени.
).(22222
)(2)(222
4
2
4
1
4
22121
4
1
3
2122
3
11
)4(
2211
bdxacxbdxxbcxxbcxacx
dxcxbxbxaxcxxbxxcxV
Примечание: цифра над равенством указывает на то, что
преобразование осуществлено с использованием формулы (4).
При выполнении условий (6) и
0, da
(3.5.1.7)
функция
0V
(определенно отрицательна).
Таким образом, при выполнении условий (6) и (7) начало
координат системы (4) будет асимптотически устойчивым при любых
начальных условиях, т.е. будет иметь место асимптотическая
устойчивость в целом (глобальная устойчивость). Теорема Ляпунова
дает достаточные условия асимптотической устойчивости.
3.5.2 Теорема Барбашина-Красовского
Теорема Ляпунова требует, чтобы в течение всего переходного
процесса было
0V
(рис. 1а). Очевидно, что в случае, изображенном
на рис. 1б, система также будет асимптотически устойчивой. Теорема
Барбашина-Красовского охватывает и этот случай.
Рассматривается система (3.5.1.1).
Теорема. Если для системы (3.5.1.1) в области
D
существует
определённо положительная функция
V
, такая, что её полная
производная по времени, взятая в силу системы (3.5.1.1), будет
знакоотрицательной (
0V
), причём множество точек, где
0V
,
не содержит целых траекторий кроме начала координат, то
положение равновесия будет асимптотически устойчиво при
начальных условиях из области
D
.
V
t
0
0V
а)
V
t
0
0V
=0
=0
б)
t
0
t
0
95
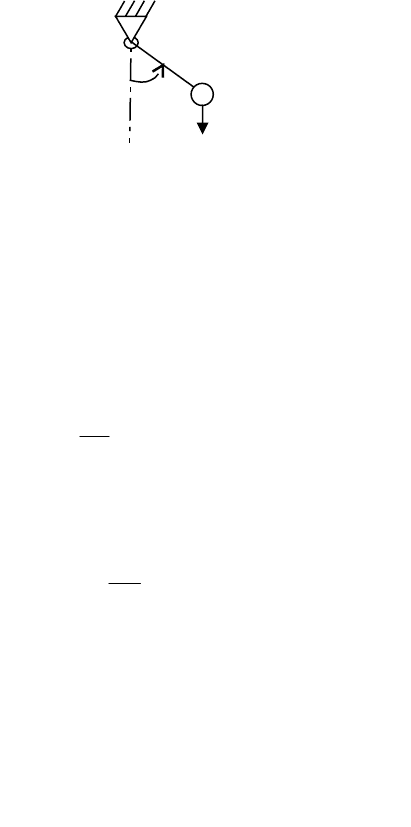
Рисунок 3.5.2.1 – Характеры изменения функции Ляпунова
Пример. Пусть дано уравнение маятника (1), изображенного на
рисунке 2.
Рисунок 3.5.2.2 – Математический маятник
0sin ybyay
, (3.5.2.1)
0, ba
. (3.5.2.2)
Умножим уравнение (1) на
y
. Получим
2
·sin yayybyy
.
Это уравнение преобразуется к виду
2
yaV
, (3.5.2.3)
где
)cos1(
2
2
yb
y
V
. (3.5.2.4)
Т.к. функция
V
обращается в 0 только при
0yy
, а во всех
остальных случаях является положительной, то функция
V
является
определённо положительной. Как видно из (4),
V
– полная энергия
системы. В данном случае
2
2
y
является кинетической энергией, а
второе слагаемое является потенциальной энергией. В правой части
(3) стоит функция рассеяния
2
yaV
. Если
0V
, то рассеяние
энергии колебаний отсутствует. Покажем, что такая ситуация может
быть только в начале координат, где
0yy
. Для этого
предположим, что
00
2
yyaV
. (3.5.2.5)
Т.к. функция
V
не зависит от
y
, то она является
знакоотрицательной. Из условия
0y
следует
у
t
0
t
0
96

cconstyy ;0
. (3.5.2.6)
Подставим (5), (6) в (1). Получим
000sin yccb
,
т.е. условие
0V
может выполняться только в начале координат.
Таким образом, выполняются все условия теоремы Барбашина-
Красовского.
Теорема Барбашина-Красовского так же, как и теорема
Ляпунова об асимптотической устойчивости, даёт достаточные
условия устойчивости. Невозможность найти функцию Ляпунова ещё
не говорит о том, что система не является асимптотически
устойчивой.
Рассмотренный пример иллюстрирует один из методов
построения функций Ляпунова. Функция Ляпунова (4)
пропорциональна полной энергии системы: сумме кинетической
(первое слагаемое) и потенциальной (второе слагаемое) энергий.
Таким образом, полная энергия системы может выступать в роли
функции Ляпунова.
3.6 Исследование устойчивости методом фазовой плоскости
Этот метод применяется к системам первого и второго
порядков. Рассмотрим методику построения фазовой плоскости
нелинейной системы второго порядка. В качестве координат примем
отклонение
q
выходной переменной от её установившегося значения
и
dtdqqr /
.
),( rqP
dt
dr
, (3.6.1)
),( rqQ
dt
dq
, (3.6.2)
где
QP,
– известные нелинейные функции. Это система второго
порядка. Разделим уравнение (1) на уравнение (2). В результате этого
исключится время.
),(:
),(
),(
rqR
rqQ
rqP
dq
dr
. (3.6.3)
Уравнение (3) является уравнением фазовой траектории в
координатах
),( rq
первого порядка. По её поведению можно судить
t
0
t
0
97

об устойчивости или неустойчивости системы.
Метод фазовой плоскости подразделяется на ряд методов.
Рассмотрим один из них.
Метод припасовывания (метод сшивания решений).
Рассмотрим нелинейную систему стабилизации
Рисунок 3.6.1 – Структурная схема нелинейной САУ
На рисунке 1
)(x
– нелинейная часть системы,
)( pW
– передаточная функция линейной части системы.
Для конкретности будем полагать
)(x
– нелинейный (релейный) регулятор,
y
– угол поворота ротора двигателя,
constg
– задающее воздействие,
x
– ошибка системы,
u
– управляющее воздействие на электродвигатель системы
(управляющее напряжение),
)( pW
– передаточная функция электродвигателя.
Эту систему опишем дифференциальными уравнениями
ygx
, (3.6.4)
)(xu
, (3.6.5)
kuyyT
. (3.6.6)
Из (4) и (6) при
constg
следует
)(xkkuxxT
. (3.6.7)
Введём новую переменную
z
. Тогда уравнение (7) можно
представить в виде системы
z
dt
dx
, (3.6.8)
)(xkz
dt
dz
T
. (3.6.9)
–
g
(x)
)1( Tpp
k
x u
y
W(p)
t
0
t
0
98
Для получения уравнений фазовых траекторий разделим уравнение (9)
на уравнение (8), получим
z
xkz
dx
dz
T
)(
. (3.6.10)
В уравнении (10) разделим переменные с учётом того, что
)(x
кусочно-постоянная функция (релейное управление).
dx
xkz
zdz
T
)(
. (3.6.11)
Для интегрирования уравнения (11) в левой и правой частях можно
применить табличные интегралы.
Рассмотрим различные релейные элементы
)(x
и
соответствующие им фазовые траектории, изображенные на рис. 2-5.
Геометрическое место точек на фазовой плоскости, в которых
происходит переключение реле, называется линией переключения
(пунктирные линии на рис. 2-5).
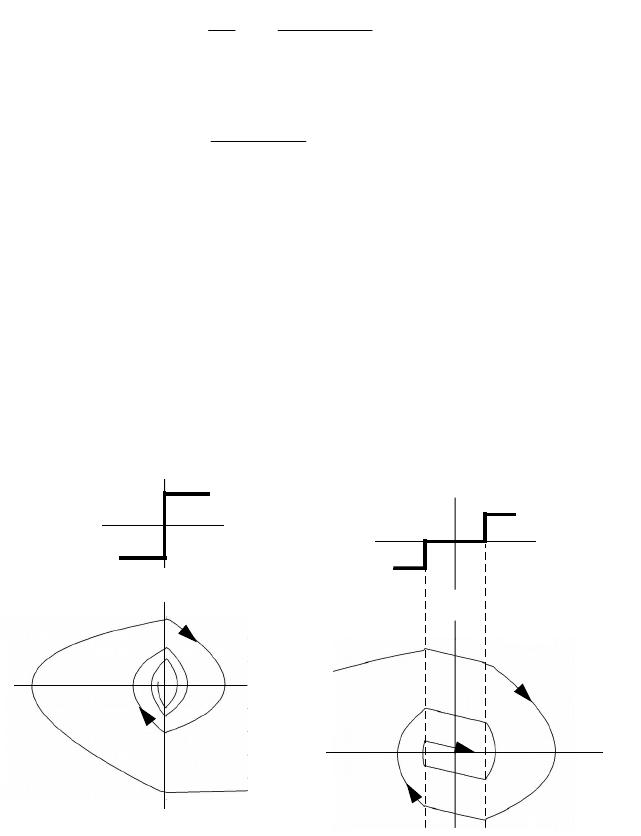
В случае рис. 2 фазовая траектория стремится к началу
координат, где, вследствие отсутствия зоны нечувствительности в
регуляторе, установится режим с высокочастотными
противовключениями электродвигателя, что нежелательно.
Рисунок 3.6.2 – а) статическая
характеристика регулятора
(двухпозиционное реле), б) фазовая
траектория
Рисунок 3.6.3 – а) статическая
характеристика регулятора
x
φ(x)
а)
x
z
б)
φ(x)
x
а)
z
x
б)
t
0
t
0
99
(трехпозиционное реле), б) фазовая траектория
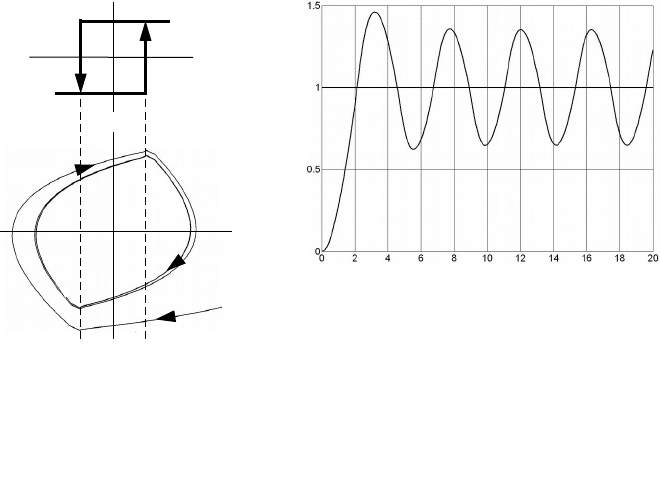
Рисунок 3.6.4 – а) статическая характеристика регулятора (двухпозиционное реле с
гистерезисом), б) фазовая траектория, в) переходный процесс
В случае рис. 3 в установившемся режиме угол поворота
двигателя будет лежать в зоне нечувствительности реле, скорость
y
будет равна нулю, электродвигатель включаться не будет.
В случае рис. 4, 5 фазовые траектории стремятся к предельному
циклу как снаружи его, так и внутри (устойчивый предельный цикл –
автоколебания).
x
φ(x)
а)
б)
x
z
y
c, t
в)
t
0
t
0
100
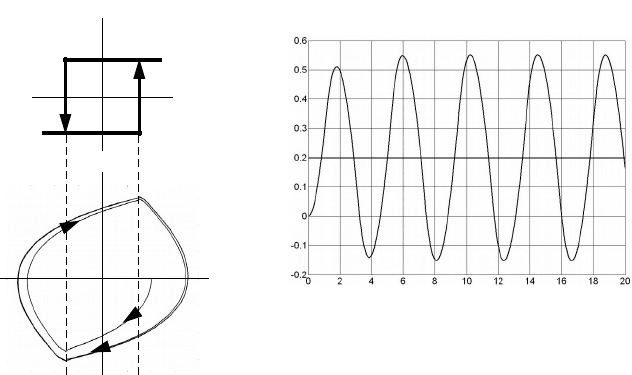
Рисунок 3.6.5 – а) статическая характеристика регулятора (двухпозиционное реле с
гистерезисом), б) фазовая траектория, в) переходный процесс
3.7 Критерий абсолютной устойчивости В.М. Пóпова
Абсолютная устойчивость – это устойчивость в целом
нелинейной системы при задании её нелинейности в определённом
классе.
Ниже будут рассматриваться статические характеристики,
лежащие в заштрихованных секторах, как это показано на рис. 1.
Таким образом, сама нелинейность не имеет конкретного вида.
О ней лишь известно, что она лежит в заданном секторе. Это является
существенным достоинством данного метода.
φ(x)
x
x
z
а)
б)
y
c, t
в)
t
0
t
0
101
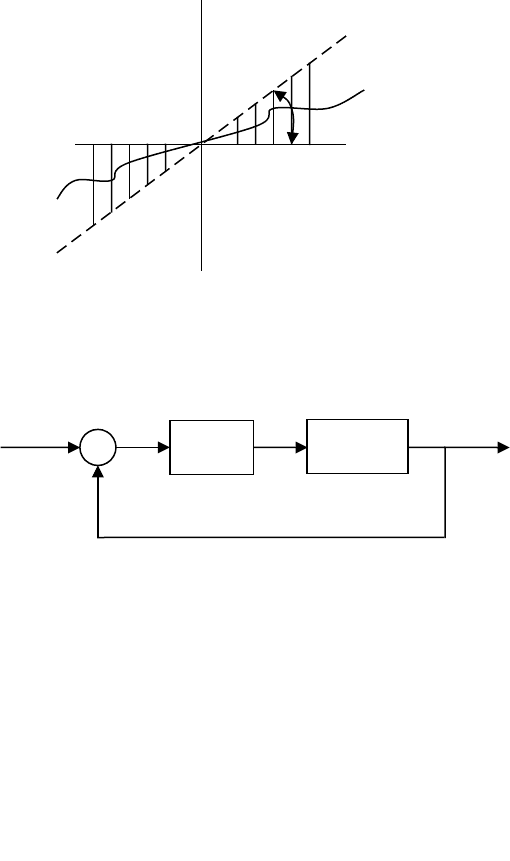
Рисунок 3.7.1 – Зона расположения статической характеристики нелинейного звена
Будем рассматривать следующую систему, представленную на
рис. 2.
Рисунок 3.7.2 – Структурная схема нелинейной САУ
На рис. 2
)(x
– статическая характеристика нелинейного звена
(например, регулятора);
)( pW
л
– передаточная функция линейной части
системы (например, объекта управления).
Для определения устойчивости по критерию Попова используется
следующая частотная характеристика Попова:
)(Im)(Re)(*
jWjjWjW
ллл
. (3.7.1)
Для сравнения приведём АФЧХ линейной части системы:
)(Im)(Re)(
jWjjWjW
ллл
. (3.7.2)
Рассмотрим вначале случай, когда линейная часть системы
устойчива (асимптотически устойчива или находится на границе
устойчивости). В этом случае критерий читается так:
(x)
x
tg
=k
g=0
(x)
x u
y
W
л
(p)
─
t
0
t
0
102
