Попов В.А. Математические методы моделирования физических процессов
Подождите немного. Документ загружается.


1
Алтайский
государственный технический
университет им. И.И. Ползунова
В.А.Попов
МАТЕМАТИЧЕСКИЕ МЕТОДЫ
МОДЕЛИРОВАНИЯ
ФИЗИЧЕСКИХ ПРОЦЕССОВ
Учебно-практическое пособие
Барнаул
2
Министерство образования Российской Федерации
Алтайский государственный технический университет
им. И.И. Ползунова
В.А. ПОПОВ
МАТЕМАТИЧЕСКИЕ МЕТОДЫ МОДЕЛИРОВАНИЯ
ФИЗИЧЕСКИХ ПРОЦЕССОВ
Учебно-практическое пособие
Барнаул 2011
3
УДК 530.1
Попов В.А. Математические методы моделирования физических процессов:
Учебно-практическое пособие /Алт. госуд. технич. ун-т им. И.И. Ползунова.
Барнаул, 2011. – 195 с.
Учебно-практическое пособие предназначено в качестве основного ма-
териала при самоподготовке к тестированию для студентов университетов
специальности: 140400 «Техническая физика». Это пособие может быть ис-
пользовано и как раздаточный материал, облегчающий труд студентов на
лекциях и лабораторных занятиях.
Весь курс разбит на шесть глав. Каждая глава начинается с формулиро-
вок определений и теорем. Приведены доказательства основных теорем.
Здесь же получены наиболее часто используемые уравнения математической
физики. Представлены методы решения этих уравнений. Завершает пособие
перечень расчетных заданий с решениями, демонстрирующими приемы при-
менения математических методов решения конкретных задач и фундамен-
тальных утверждений, используемых при моделировании физических про-
цессов.
4
1 Уравнения математической физики
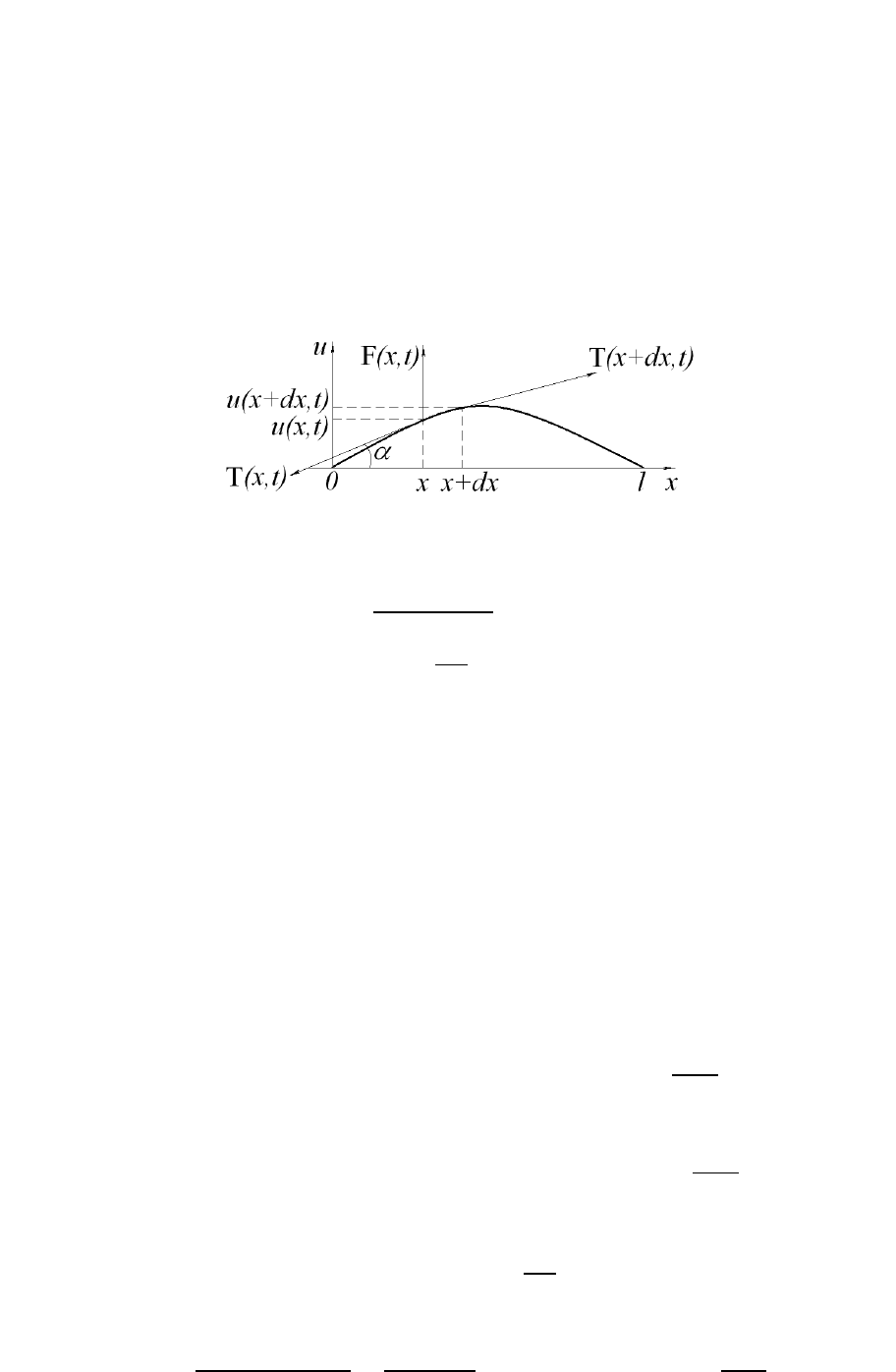
1.1 Уравнение малых поперечных колебаний струны
Струной в теории колебаний называют тонкую, гибкую, сильно натя-
нутую нить с равномерно распределенной по длине плотностью. При воз-
буждении струны, например ударом или щипком, она начинает совершать
колебательные движения, при которых все ее участки смещаются в попереч-
ном направлении. Описание процесса колебаний может быть проведено при
помощи задания положения точек струны в различные моменты времени.
Пусть точки струны испытывают смещения в одной плоскости . Тогда
функция характеризует вертикальное смещение. Длина дуги любого
участка от
до
равна
∫
√
(
)
Следовательно, при столь малых колебаниях удлинения, можно считать, не
происходит. И в соответствии с законом Гука натяжение остается постоян-
ным:
Обозначим через линейную плотность внешних сил в точке в мо-
мент времени , направленных перпендикулярно оси , а через – линейную
плотность струны. На участок струны c координатами концов и
действуют силы натяжения
,
и внешние силы с линейной
плотностью этих сил
. В соответствии с вторым законом Ньютона
уравнение движения этого участка запишем в виде:
Или в проекциях на ось
|
|
При малых колебаниях можно считать, что
Тогда
(
)
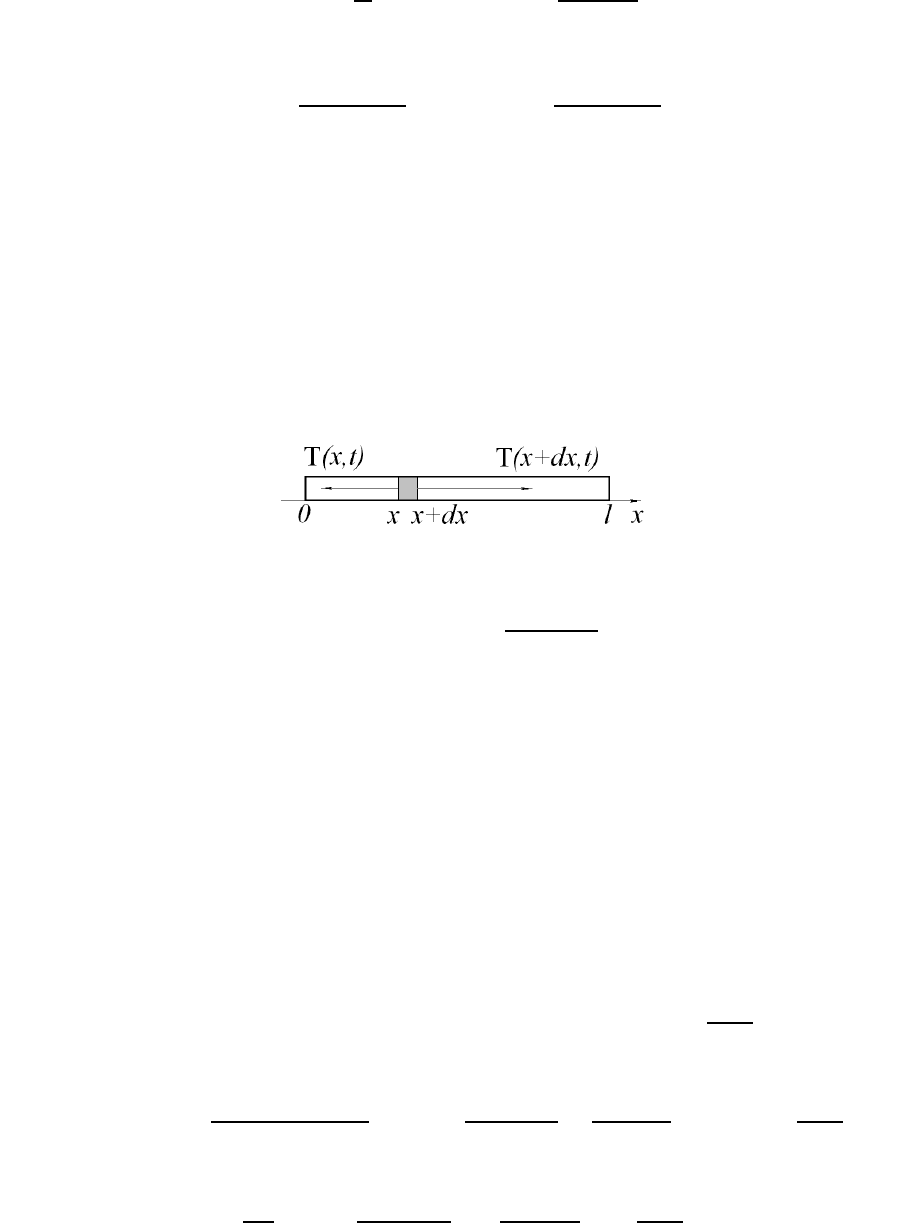
5
Введем обозначения:
и получим одномерное волновое уравнение:
1.2 Уравнение малых продольных колебаний стержня
Стержнем в теории колебаний называют упругое твердое тело, длина
которого значительно превышает его поперечные размеры. При возбуждении
стержня, например ударом, в нем возникают колебания. Колебательные сме-
щения частиц стержня могут быть направлены как вдоль оси – продольные
колебания, так и перпендикулярно оси – крутильные и изгибные колебания.
При продольных колебаниях частицы стержня перемещаются вдоль оси .
Напряжения в соответствии с законом Гука равны
Здесь коэффициент пропорциональности
между механическим напря-
жением
и относительным смещением частиц называется
модулем Юнга или модулем продольной упругости материала. Под механи-
ческим напряжением в простейшем случае применительно к стержню будем
понимать величину упругой силы, действующей на единицу площади попе-
речного сечения стержня. Пусть на участок стержня поперечного сечения c
координатами концов и действуют силы с напряжением
,
и внешние силы с линейной плотностью этих сил
. В со-
ответствии с вторым законом Ньютона уравнение движения этого участка
запишем в виде:
Или с использованием закона Гука
Полученное уравнение может быть преобразовано к форме:
(
)
В частности, при и
получим одномерное волновое
уравнение:
6
Здесь введены обозначения:
1.3 Уравнение электрических колебаний в проводах
Прохождение электрического тока по проводу с распределенными па-
раметрами характеризуется силой тока и электрическим напряжением ,
которые являются функциями координаты и времени . Силой тока назы-
вается скалярная величина, равная отношению заряда , переносимого че-
рез сечение проводника за интервал времени , к этому интервалу времени:
. Электрическое напряжение между двумя точками электриче-
ской цепи равно работе электрического поля по перемещению единичного
положительного заряда из одной точки в другую. Применим закон Ома к
участку провода длиной :
Здесь – сопротивление и индуктивность провода единичной длины. Ко-
личество электричества, протекающего через элемент провода длиной ,
представим в виде:
где
– заряд, поступивший в элемент провода за промежуток време-
ни ,
– заряд, покинувший этот же элемент провода за этот
же промежуток времени. С другой стороны, это же количество электричества
необходимо для зарядки этого элемента провода до потенциала, равного , с
учетом потери заряда вследствие несовершенства изоляции:
(
)
или
(
)
Здесь – емкость и утечка провода единичной длины. Полученные урав-
нения, которые представим в следующем виде:
образуют систему телеграфных уравнений.
Продифференцируем второе из этих уравнений по и, умножив его на
, вычтем из первого, продифференцированного по . Получим
7
Подставим из второго равенства системы телеграфных уравне-
ний. Получим уравнение для тока:
Аналогично можно получить и выражение для напряжения:
Последние два уравнения называют телеграфными уравнениями для тока и
напряжения соответственно. Заметим, что с точностью до обозначений эти
уравнения совпадают. Поэтому в дальнейшем понимая под
силу тока
или напряжение
будем называть телеграфным уравнением
уравнение вида:
Здесь введены следующие обозначения:
, , .
Если пренебречь утечками и сопротивлением провода, то придем к однород-
ному волновому уравнению
1.4 Уравнение малых поперечных колебаний мембраны
Мембраной в теории колебаний называют гибкую тонкую пленку,
приведенную внешними силами в состояние натяжения и обладающая вслед-
ствие этого упругостью. Пусть мембрана, натянутая на контур , лежащий в
плоскости , испытывает вертикальные смещения
. Вектор
натяжения направлен по нормали к контуру и лежит в плоскости, каса-
тельной к мембране вследствие отсутствия сопротивления изгибу и сдвигу.
Пусть – элемент дуги некоторого контура, взятого на поверхности мем-
браны. Отсутствие сопротивления сдвигу приводит к тому, что величина
натяжения не зависит от направления нормали к элементу , а сам вектор
натяжения является функцией координат и времени:
. Будем
рассматривать малые колебания, пренебрегая квадратами ,
. Тогда проекция вектора натяжения на плоскость равна са-
мому натяжению
, а вертикальная составляющая равна нормальной
составляющей:
(
)
Выберем контур так, чтобы его проекция на плоскость представляла со-
бой прямоугольник со сторонами, равными
,
. Сила натя-
жения этого контура:

8
∮
при отсутствии перемещения вдоль
∫
(
)
а при отсутствии перемещения вдоль
∫
(
)
Применим к двум последним равенствам теорему о среднем. В силу произ-
вольности в выборе площадки получаем
Отсюда следует, что натяжение зависит только от времени. Площадь каждого
элемента мембраны при малых колебаниях можно считать неизменной:
∬
√
(
)
(
)
∬
Тогда, в соответствии с законом Гука, можно считать неизменным и натяже-
ние мембраны:
Далее воспользуемся вторым Нью-
тона, согласно которому изменение количества движения участка мембраны
равно импульсу всех внешних сил и сил натяжения:
∬
(
)
∫
.
∮
∬
/
Здесь
– проекция участка мембраны на плоскость ,
– граница этого
участка,
[
]
– произвольный промежуток времени,
– поверхност-
ная плотность мембраны,
– плотность внешних сил. Для смещений
, имеющих непрерывные вторые производные, справедлива теорема
Остроградского:
∮
∬
(
)
C другой стороны,
∫
Тогда
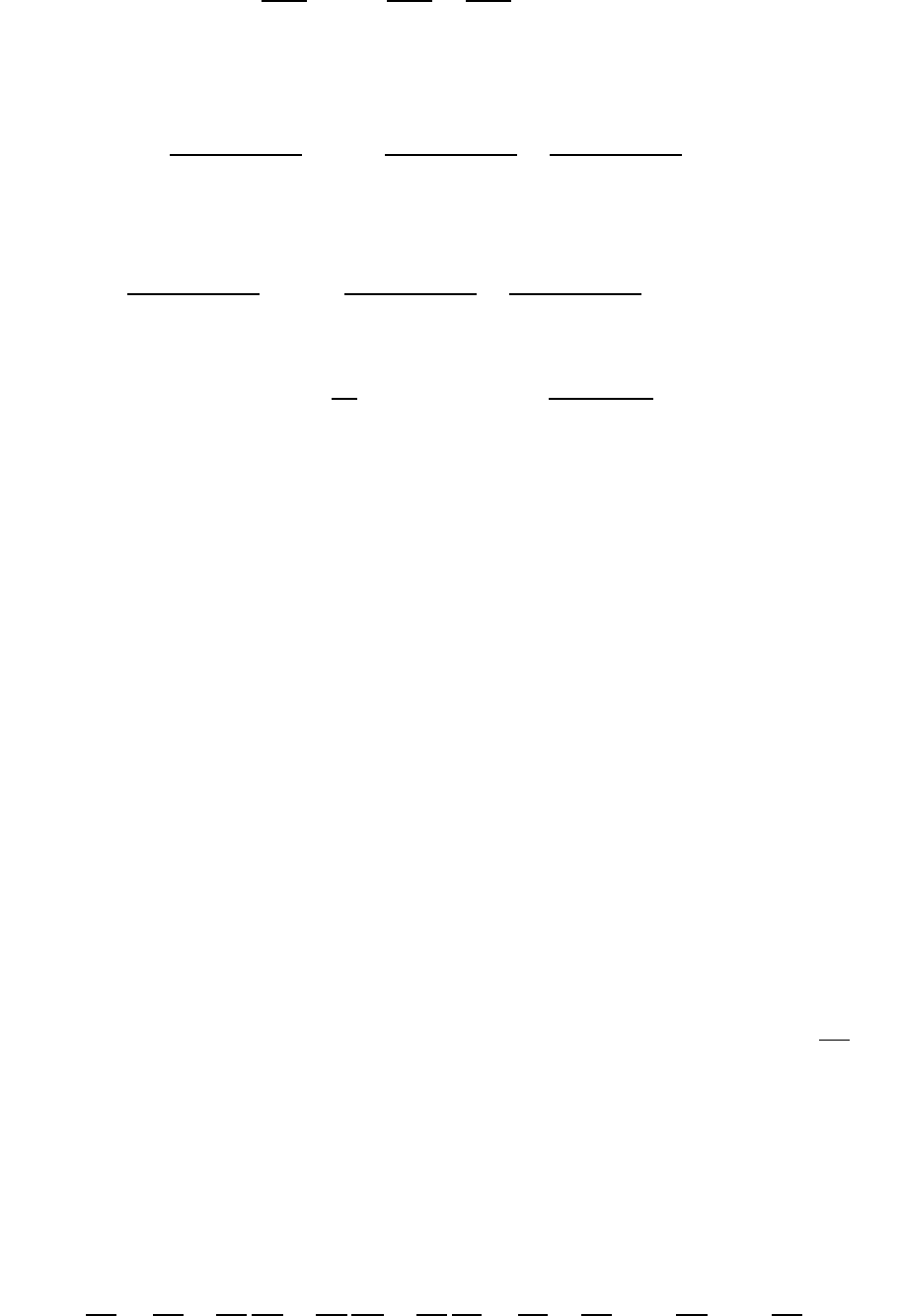
9
∫∬
(
(
)
)
Применим теорему о среднем, учтем произвольность выбора
и
[
]
, по-
лучим
(
)
В частности, при
получим двумерное волновое уравне-
ние:
(
)
Здесь введены следующие обозначения:
1.5 Уравнения гидродинамики и акустики
Движущуюся жидкость будем характеризовать следующими величи-
нами:
– плотностью,
– давлением и вектором скорости
. Обозначим
– плотность внешних сил, по определению равную силе, действующей на
единицу массы вещества. Рассмотрим идеальную жидкость – лишенную
вязкости и теплопроводности. Выделим в ней некоторый объем , ограни-
ченный поверхностью . В соответствии с теоремой о градиенте силу давле-
ния, оказываемого на поверхность , можно представить в виде:
∬
∭
Здесь – единичный вектор нормали, внешней по отношению к поверхности
. В соответствии со вторым законом Ньютона уравнение движения жидко-
сти под действием всех внешних сил и сил давления можно представить в
виде:
∭
∭
∭
При вычислении ускорения некоторой точки жидкости , стоящего в
правой части равенства, необходимо учитывать перемещение самой этой
точки. Пусть уравнения траектории точки в декартовой системе координат
имеют вид:
Тогда
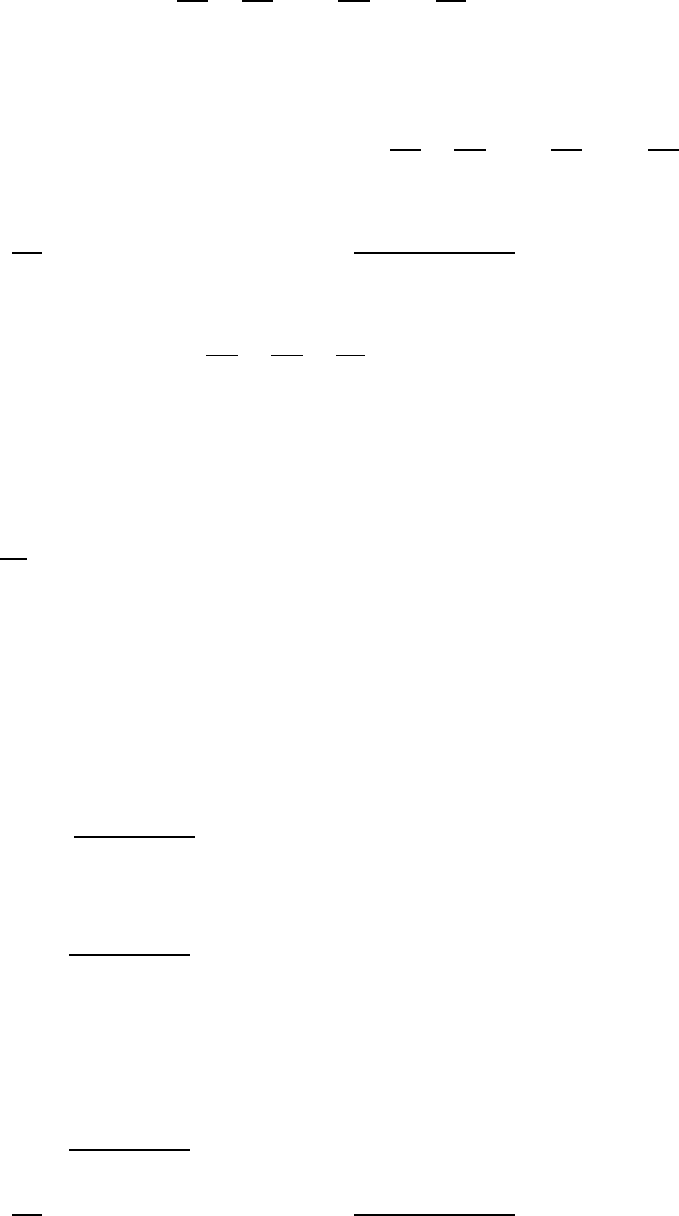
10
В силу произвольности объема из полученного уравнения движения жидко-
сти, записанного в интегральной форме
∭
∭
∭
(
)
следует уравнение, известное в гидродинамике под названием уравнение
Эйлера:
(
)
Или в более краткой форме записи:
Здесь оператор имеет вид:
Если внутри объема нет источников и стоков вещества, то в соответ-
ствии с законом сохранения количества вещества изменение количества
жидкости в этом объеме в единицу времени равно потоку жидкости через
границу :
∭
∯
Правую часть этого равенства преобразуем в соответствии с теоремой о ди-
вергенции:
∯
∭
Получим уравнение
∭
(
)
справедливое для любых объемов. В силу произвольности объема , имеем
Полученное уравнение называют уравнением непрерывности, или уравне-
нием неразрывности. Уравнение неразрывности и уравнение Эйлера сов-
местно с уравнением состояния
образуют замкнутую систему
уравнений гидродинамики:
