Попов В.А. Математические методы моделирования физических процессов

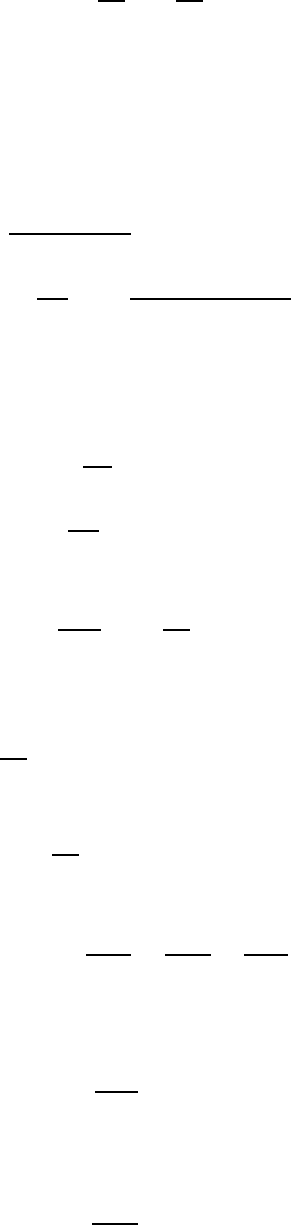
11

Для получения уравнения состояния

требуется привлечь до-

полнительные утверждения. Например, при описании распространения звука

в газе, можно воспользоваться уравнением адиабаты:

(

)

где

,

, - известные величины. Введем величину относительного откло-

нения плотности от начального значения

:

. Тогда

при небольших давлениях газа, в котором отсутствуют внешние силы, прене-

брегая высшими степенями скоростей и изменением плотности, запишем си-

стему уравнений гидродинамики в виде:

Обозначим

и преобразуем систему уравнений гидродинамики в

следующей форме:

Продифференцируем по времени обе части первого уравнения. Получим

Ко второму уравнению применим операцию вычисления дивергенции, затем

поменяем порядок дифференцирования. Результат запишем в виде:

или

Здесь оператор Лапласа имеет вид:

Сопоставляя результаты преобразования первого и второго уравнения гидро-

динамики, получим

Или для плотности

трехмерное однородное волновое уравне-

ние:

12

1.6 Начальные и граничные условия

При математическом описании физического процесса надо поставить

задачу, то есть сформулировать условия, достаточные для однозначного

описания процесса. Для этого необходимо иметь не только уравнения, явля-

ющиеся математической моделью процесса, но и задать дополнительные

условия (начальные и граничные), описывающие влияние внешних условий

на протекание процесса в изучаемом объекте.

Сформулируем начальные условия на примере поперечных колеба-

ний струны, описываемых уравнением:

Сам процесс колебаний зависит от начальных отклонений и начальных ско-

ростей всех точек струны при :

|

В случае бесконечной протяженности объекта, либо когда граничные

условия в точке, достаточно удаленной от границ, сказываются через боль-

шой промежуток времени, а также для малых промежутков времени, когда

влияние границ не существенно, решают задачу с одними начальными усло-

виями – задачу Коши. Формулировка задачи Коши: Найти решение урав-

нения

при с начальными условиями:

|

Граничные условия первого рода рассмотрим на примере попереч-

ных колебаний струны. Если концы струны закреплены, то смещение этих

концов равно нулю:

В этом случае говорят об однородных граничных условиях первого рода

условно закрепленных концов. В более общем случае, когда концы движутся

по заданному закону, граничные условия можно записать в виде:

В этом случае говорят о граничных условиях заданного режима. Формули-

ровка первой краевой задачи: Найти

, удовлетворяющую уравнению

в области при начальных условиях

|

и граничных условиях первого рода:

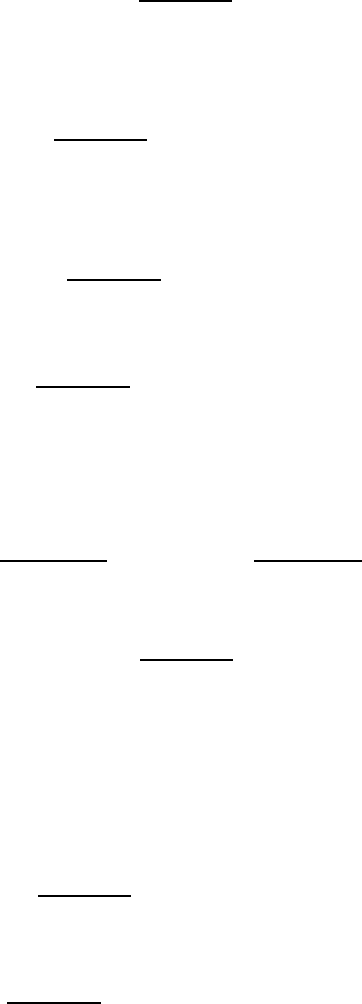
13

Граничные условия второго рода рассмотрим на примере продоль-

ных колебаний стержня. Пусть один конец струны закреплен, а другой сво-

боден. Тогда на свободном конце закон движения не задан и является иско-

мой функцией. Однако сила натяжения на свободном конце равна нулю, так

как на него не действуют извне никакие силы:

|

Так как модуль Юнга

математическое условие свободного конца

формулируется следующим образом:

|

В более общем случае, когда на этот же конец действует сила ̃

, вызыва-

ющая, согласно третьему закону Ньютона, натяжение

|

̃

граничное условие второго рода представимо в виде:

|

где

̃

. В этом случае говорят об условии заданной силы.

Формулировка второй краевой задачи: Найти

, удовлетворяющую

уравнению

в области при начальных условиях

|

и граничных условиях второго рода:

Граничные условия третьего рода рассмотрим на примере продоль-

ных колебаний стержня. Пусть на один из концов струны действует упругая

сила

|

или

|

где

. Коэффициент называется коэффициентом жесткости за-

крепления. В более общем случае, когда точка закрепления сама перемеща-

ется и ее отклонение задается функцией

, то условие третьего рода при-

мет вид

14

|

(

)

Формулировка третьей краевой задачи: Найти

, удовлетворяющую

уравнению

в области при начальных условиях

|

и граничных условиях третьего рода:

|

(

)

|

(

)

Если при и при граничные условия имеют различные типы,

то такие задачи называют смешанными задачами. Комбинируя различные

условия, получаем различные типы краевых задач.

Кроме вышеназванных типов часто рассматривают задачи, в которых

явление изучается вблизи одной границы и влияние другой несущественно.

Такие задачи называются задачами на полуограниченной прямой. Задачи

без начальных условий называют задачами на установившийся режим.

1.7 Уравнение теплопроводности

Пусть

– температура среды в точке с координатами

в момент времени . Под температурой будем понимать физическую вели-

чину, характеризующую состояние термодинамического равновесия макро-

скопической системы, равную производной от энергии тела по его энтропии.

Под теплотой будем понимать количество тепловой энергии, переданное си-

стемой при теплообмене. Выделим произвольный объем , ограниченный

поверхностью . В соответствии с законом Фурье количество теплоты

,

переданное через элемент поверхности за время , пропорционально

потоку температурного градиента

и времени наблюде-

ния :

Здесь , – вектор единичной нормали, внешней по отношению к

замкнутой поверхности ,

– коэффициент теплопровод-

ности. Знак минус соответствует тому, что тепловые потоки идут от участков

с более высокой температурой к участкам с более низкой температурой, то

есть в направлении, противоположном температурному градиенту .

Внутрь объема через всю поверхность за время наблюдения от

до

поступит количество теплоты, равное

15

∫∯

Или, в соответствии с теоремой о дивергенции:

∯

∭

перейдем к интегрирования по объему , охватываемому поверхностью .

Получим

∫∭

(

)

Определим функцию источника тепла

, равную количеству теп-

ла, выделяющегося (поглощающегося) в единице объема в единицу времени.

Тогда количество тепла, выделяющегося (поглощающегося) во всем объеме

за время наблюдения от

до

, равно

∫∭

Воспользуемся определением удельной теплоемкости

, равной ко-

личеству тепла, которое необходимо подвести к телу единичной массы, что-

бы увеличить его температуру на единицу. В соответствии с этим определе-

нием запишем суммарное количество тепла, пошедшее на изменение темпе-

ратуры во всем объеме :

∭

(

)

Или

∫∭

Итак, в соответствии с законом сохранения энергии, количество тепловой

энергии

, которое пошло на изменение температуры за время наблюдения

от

до

, равно сумме тепловой энергии

, прошедшей за это время через

поверхность в объем и количеству тепловой энергии, выделенной за это

же время распределенными в объеме источниками тепла:

,

или

∫∭

(

)

∫∭

(

))

16

В силу произвольности объема и промежутка времени, подынтегральные

функции должны быть также равны:

(

)

Полученное уравнение представляет собой уравнение теплопроводности.

Заметим, что если среда однородная, то постоянны и уравнение

теплопроводности выглядит следующим образом:

где

. Функцию

часто называют

плотностью источников. Если в среде нет источников (холодильников), то

и мы имеем однородное уравнение теплопроводности:

1.8 Уравнение диффузии

Диффузия – это явление взаимного проникновения соприкасающихся

веществ друг в друга вследствие теплового движения частиц вещества. Диф-

фузия происходит в направлении уменьшения концентрации вещества и ве-

дет к его равномерному распределению по занимаемому объему. Диффузия

имеет место в газах, жидкостях и твердых телах. Диффундировать могут как

находящиеся в них частицы посторонних веществ, так и собственные части-

цы. В частности, диффузия в чистом веществе или растворе постоянного со-

става, при котором диффундируют собственные частицы вещества, называ-

ется самодиффузией.

Пусть

– концентрация -го компонента вещества в точке с

координатами

в момент времени . Под концентрацией будем по-

нимать физическую величину, определяющую содержание компонента в

смеси, растворе, сплаве, численно равную отношению массы компонента к

общей массе смеси. Выделим произвольный объем , ограниченный поверх-

ностью . В соответствии с законом Фика масса этого компонента , про-

никшая через элемент поверхности за время , пропорциональна пото-

ку концентрационного градиента

и времени наблюде-

ния :

Здесь , – вектор единичной нормали, внешней по отношению к

замкнутой поверхности ,

– коэффициент диффузии.

Знак минус соответствует тому, что диффузионные потоки направлены от

участков с более высокой концентрации к участкам с более низкой концен-

трации, то есть в направлении, противоположном градиенту концентрации

. Внутрь объема через всю поверхность за время наблюдения от

до

поступит количество вещества данного компонента, равное

17

∫∯

Или, в соответствии с теоремой о дивергенции:

∯

∭

перейдем к интегрирования по объему , охватываемому поверхностью .

Получим

∫∭

(

)

Определим функцию источника

, равную количеству вещества

этого компонента, появляющегося (исчезающего), например, в результате

химической реакции, в единице объема в единицу времени. Тогда количество

вещества -го компонента, появляющегося (исчезающего) во всем объеме за

время наблюдения от

до

, равно

∫∭

Воспользуемся определением плотности -го компонента вещества

, равной массе -го компонента этого вещества в единице объема.

В соответствии с этим определением запишем суммарное изменение массы

вещества -го компонента в объеме за время от

до

:

∭

(

)

Или

∭

(

)

В соответствии с законом сохранения вещества, суммарное изменение коли-

чества вещества -го компонента

в объеме за время от

до

равно ко-

личеству вещества -го компонента, поступившего через всю поверхность ,

и появившегося (исчезнувшего) за счет источников (стоков) вещества во

всем объеме за это же время наблюдения:

, или

∫∭

(

)

∫∭

(

))

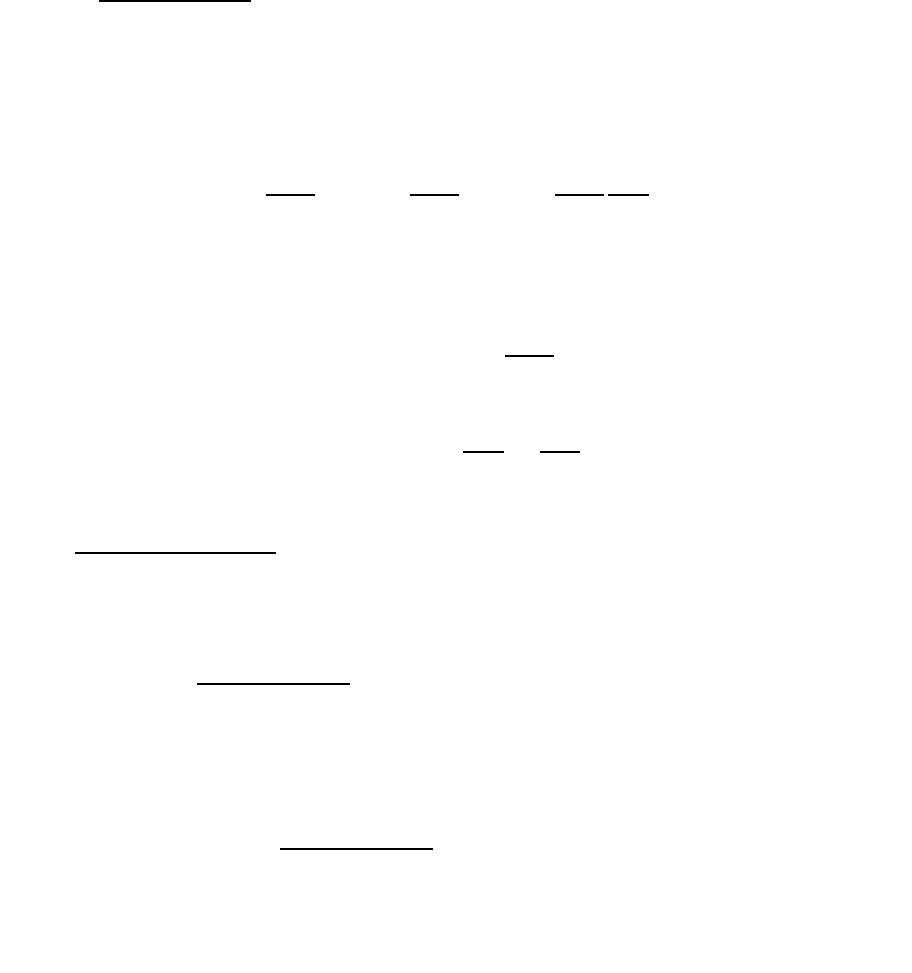
18

В силу произвольности объема и промежутка времени, подынтегральные

функции должны быть также равны:

(

)

В полученном уравнении диффузии можно выразить плотность -го компо-

нента

через концентрацию -го компонента вещества

. Для этого воспользуемся определением плотности -го

компонента вещества:

Здесь использованы обозначения: – масса вещества в объеме ,

–

масса -го компонента вещества в объеме , определение концентрации -го

компонента:

и плотности вещества:

Тогда

(

)

(

)

Представленное здесь уравнение диффузии может быть упрощено, если и

постоянны. Запишем его в виде:

где

. Функцию

часто называют плот-

ностью источников. Если в среде нет источников или стоков -го компонента

вещества, то

и мы имеем однородное уравнение диффузии:

1.9 Краевые условия уравнения диффузии и теплопроводности

Отметим, что формы записи уравнений переноса тепла и массы одина-

ковы. Одинаковую форму имеют и краевые условия, под которыми пони-

мают задание начальных и граничных условий.

Начальные условия, как правило, не отличаются разнообразием.

Обычно задается поле температур или концентраций в начальный момент

времени. Однако имеется большой класс процессов, в которых начальные

условия играют второстепенную роль. Их называют регулярными процес-

сами, или режимами, при которых система успела «забыть» начальное рас-

пределение, либо начальные условия вообще не играют никакой роли.

Например, при установившихся периодических процессах.

19

Граничными условиями первого рода в математике называют, как

известно, условия, при которых задаются поля изучаемых величин на по-

верхности. Таким образом, для уравнения теплопроводности задается темпе-

ратура на поверхности, для уравнения диффузии – концентрация.

Граничными условиями второго рода в математике называют усло-

вия, при которых задаются потоки изучаемых величин на поверхности. Для

уравнения теплопроводности задается тепловой поток, по определению рав-

ный количеству тепла, переданному через изотермическую поверхность в

единицу времени. В соответствии с законом Фурье тепловой поток пропор-

ционален градиенту температур, поэтому граничное условие второго рода

для уравнения теплопроводности формулируется как задание производных

от температуры по координатам на поверхности. Для уравнения диффузии

задается поток вещества, по определению равный массе вещества, перене-

сенного через поверхность в единицу времени. В соответствии с законом

Фика поток вещества пропорционален градиенту концентрации, поэтому

граничное условие второго рода для уравнения диффузии формулируется как

задание производных от концентрации по координатам на поверхности.

Граничные условия третьего рода рассмотрим после граничных усло-

вий четвертого рода. Граничные условия четвертого рода – это условия

«сшивания» решений уравнения на границе двух сред. Условия, при которых

нет скачка искомой функции на поверхности раздела сред, называют еще

условием идеального контакта. Граничные условия четвертого рода могут

быть сформулированы и как равенство потоков на границе. Постановка таких

граничных условий, отличных от идеальных, может быть связана с плохим

механическим контактом соприкасающихся поверхностей, с наличием тон-

кого слоя окисла, с возможностью образования многослойной границы после

химической реакции веществ соприкасающихся поверхностей и др. Гранич-

ные условия четвертого рода, сформулированные как равенство потоков на

границе, также могут нарушаться. Например, при наличии поверхностных

источников или стоков, появившихся в результате химических реакций на

поверхности, в том числе и с участием вещества поверхности. Таким обра-

зом, использование граничных условий четвертого рода возможны лишь для

ограниченного числа самых простых задач.

Для практического использования наиболее пригодны граничные

условия третьего рода – это искусственный способ обойти сложности, воз-

никающие при последовательной и строгой постановке задач с граничными

условиями четвертого рода. Формулировка граничных условий третьего рода

для уравнения теплопроводности основана на законе теплообмена Ньюто-

на, согласно которому поток тепла пропорционален разности температур тел:

Это приближенное эмпирическое соотношение имеет весьма ограниченную и

не четкую область применимости. Коэффициент теплообмена не является

характеристикой среды, он характеризует процесс и может зависеть от

свойств стенки, температуры и скорости набегающего на стенку потока. Бо-

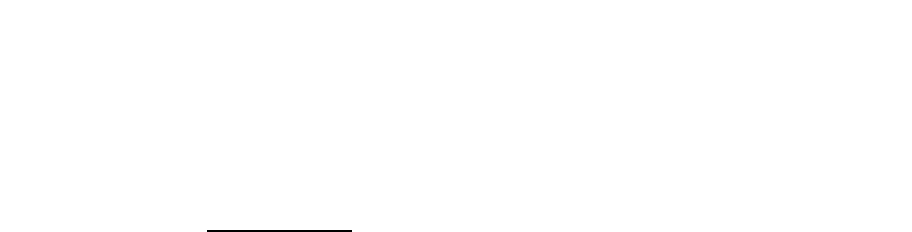
20

лее того, он может оказаться зависящим от времени. Таким образом, в коэф-

фициенте теплообмена содержатся все сложности реального процесса теп-

лообмена. И трудность решения задач теплообмена здесь фактически пере-

ложена на эксперимент – на необходимость определять в конкретных про-

цессах. Закон теплообмена Ньютона и есть граничное условие третьего рода

для задач теплообмена. Аналогичное условие есть и для задач массообмена.

Это так называемый закон Дальтона, согласно которому скорость испарения

вещества пропорциональна превышению парциального давления паров над

стенкой относительно давления

насыщенных паров при данной темпера-

туре:

Коэффициент

называют коэффициентом тепло-

обмена. И все вышеуказанное о законе теплообмена Ньютона можно повто-

рить относительно закона Дальтона, который может служить граничным

условием третьего рода для задач массообмена.

Четыре рода граничных условий отнюдь не исчерпывают все многооб-

разие задач теплопроводности и диффузии. Это лишь самые распространен-

ные, «типовые» граничные условия. В практике можно встретить много

иных. Например, теплообмен излучением между твердыми телами определя-

ется законом Стефана-Больцмана, согласно которому поток тепла пропор-

ционален разности четвертой степени температуры тел:

Все

вышеуказанное о законе теплообмена Ньютона можно повторить относи-

тельно закона Стефана-Больцмана, который может служить граничным усло-

вием третьего рода для задач теплообмена.

Все изложенное выше относится к так называемым прямым задачам

теплопроводности и диффузии – задачам определения полей температуры и

концентрации соответственно по заданным граничным условиям. В жизни

приходится сталкиваться с обратными задачами, когда поле температур в

некоторых точках системы в зависимости от времени известно и требуется

получить сведения о граничных условиях, например определить потоки теп-

ла на поверхности. С такой задачей приходится встречаться при эксперимен-

тальном изучении теплообмена летательных аппаратов. Обратные задачи яв-

ляются гораздо более сложными, чем прямые. В общей постановке они при-

надлежат к числу «некорректных» задач математической физики. Сложность

таких задач в устойчивости решений. Малые изменения задаваемого поля

температур могут привести к значительным изменениям изучаемых функций.

1.10 Стационарное тепловое поле

При изучении распределения тепла в некоторой среде часто употреб-

ляют понятие теплового поля, которое характеризуется температурой в

каждой точке, в каждый момент времени. Для однородной среды тепловое

поле описывается уравнением теплопроводности:

Попов В.А. Математические методы моделирования физических процессов

Подождите немного. Документ загружается.