Попов В.А. Математические методы моделирования физических процессов
Подождите немного. Документ загружается.


31
Подставляя это произведение в уравнение свободных колебаний струны, по-
лучим
или
Последнее равенство, левая часть которого зависит только от ,а правая –
только от , возможно лишь в том случае, если обе части его не зависят ни от
, ни от , т. е. представляют собой одну и ту же постоянную. Обозначим эту
постоянную через . Тогда получим два обыкновенных дифференциальных
уравнения
Те значения параметра , при которых уравнения имеют нетривиальные ре-
шения, называются собственными числами (или значениями), а сами эти
решения – собственными функциями. Для отыскания собственных значе-
ний и собственных функций полученных обыкновенных дифференциальных
уравнений рассмотрим отдельно три случая, когда и
1. При общее решение уравнения
имеет вид
√
√
Удовлетворяя это решение граничным условиям
,
, получим
√
√
Так как решением этой системы являются значения
, то
.
2. При общее решение уравнения
имеет вид
Удовлетворяя это решение граничным условиям
,
, получим
Так как решением этой системы являются значения
, то
.
3. При общее решение уравнения
имеет вид
(
√
)
(
√
)
Удовлетворяя это решение граничным условиям
,
, получим
(
√
)
(
√
)
Отсюда следует, что
и
(
√
)
Если
то опять придем к
тривиальному решению
, поэтому будем считать, что
.
Отыскание ненулевого решения краевой задачи называется задачей
Штурма-Лиувилля. Итак, ненулевые решения уравнения
возможны лишь при
(
√
)
, то есть при таких значениях , которые
удовлетворяют условию
(
)
Этим собственным числам соответствуют собственные функции
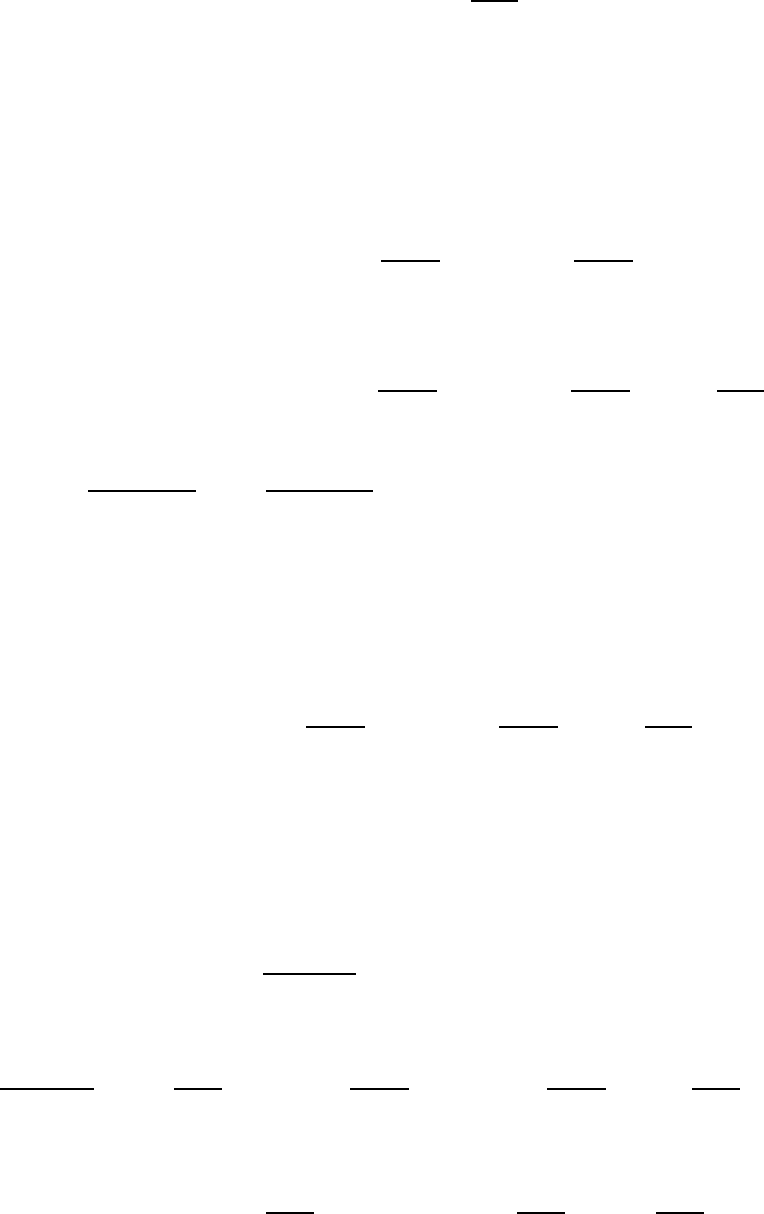
32
(
)
определяемые с точностью до постоянного множителя, который мы положи-
ли равным единице. Заметим, что положительные и отрицательные значения
, равные по абсолютной величине, дают собственные функции, отличающи-
еся лишь постоянным множителем. Поэтому достаточно для брать только
целые положительные значения.
При
общее решение уравнения
имеет вид
(
)
(
)
где
и
– произвольные постоянные.
Таким образом, функции
(
(
)
(
))
(
)
удовлетворяют уравнению
с закрепленными концами
при любых
и
. В силу линейности и однородности уравнения свобод-
ных колебаний струны всякая конечная сумма решений будет также решени-
ем этого уравнения. То же справедливо и для ряда
∑(
(
)
(
))
(
)
если он сходится и его можно дважды почленно дифференцировать по и .
Поскольку каждое слагаемое в этом ряде удовлетворяет граничным услови-
ям, то этим условиям будет удовлетворять и сумма ряда, т. е. функция
.
Остается определить постоянные
и
так, чтобы удовлетворялись и
начальные условия:
|
Продифференцируем полученный ряд по :
∑
(
(
)
(
))
(
)
и в силу начальных условий получим
∑
(
)
∑
(
)
Это ни что иное как разложение заданных функций
и
в ряд
Фурье по синусам в интервале
. Коэффициенты разложения определя-
ются по известным формулам:

33
∫
(
)
∫
(
)
Покажем, что представление решения уравнения свободных колебаний
струны в виде ряда
∑(
(
)
(
))
(
)
а также ряд, полученный почленным дифференцированием его два раза по ,
и ряд, полученный почленным дифференцированием его два раза по , абсо-
лютно и равномерно сходятся. Для этого выполним трижды интегрирование
по частям выражения для коэффициентов
∫
(
)
(
)
и дважды – интегрирование по частям выражения для коэффициентов
∫
(
)
(
)
Здесь использованы условия
а также обозначения
∫
(
)
∫
(
)
Согласно равенству Парсеваля, ряды
∑
|
|
∑
|
|
сходятся. Таким образом, полученный ряд
(
)
∑
(
(
)
(
))
(
)
мажорируется сходящимся рядом
(
)
∑
(
|
| |
|
)
(
)
Следовательно, решение уравнения свободных колебаний струны может
быть представлено в виде сходящегося ряда.
1.19 Решение задачи о колебании мембраны методом Фурье
Рассмотрим задачу о колебании прямоугольной мембраны, закреплен-
ной по периметру. Если предположить, что при равновесии мембрана нахо-
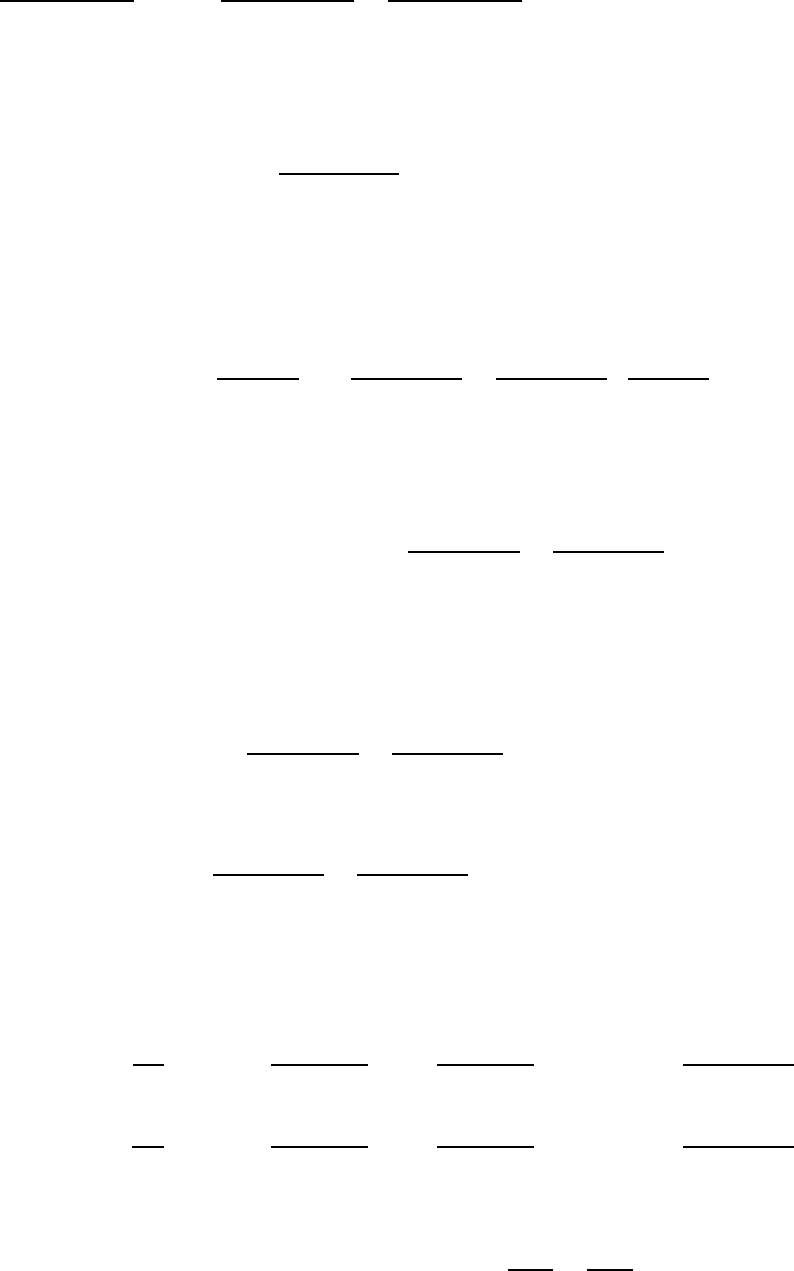
34
дится в плоскости , и – величина отклонения точки с координа-
той , в момент времени от положения равновесия, то эта задача сводится
к решению волнового уравнения
(
)
закрепленной по периметру мембраны
при начальных условиях
|
Будем искать нетривиальное решение волнового уравнения, удовлетворяю-
щее вышеуказанным граничным и начальным условиям, в виде произведения
двух функций: . Подставляя эту функцию в волновое
уравнение и разделяя переменные, получим
(
)
Рассуждая как и ранее, будем утверждать, что равенство возможно только в
том случае, когда обе части этого равенства равны одной и той же постоян-
ной, которую обозначим через . Тогда получим два уравнения:
Таким образом, как и ранее пришли к задаче Штурма-Лиувилля по отыска-
нию нетривиального решения краевой задачи. Для того, чтобы определить
знак
, при котором могут существовать нетривиальные решения, умножим
уравнение
на
и проинтегрируем по прямоугольнику:
∫∫
(
)
∫∫
Учитывая граничные условия
и тождества
(
)
(
)
(
)
(
)
получаем, что
∫∫
∫∫
(
)
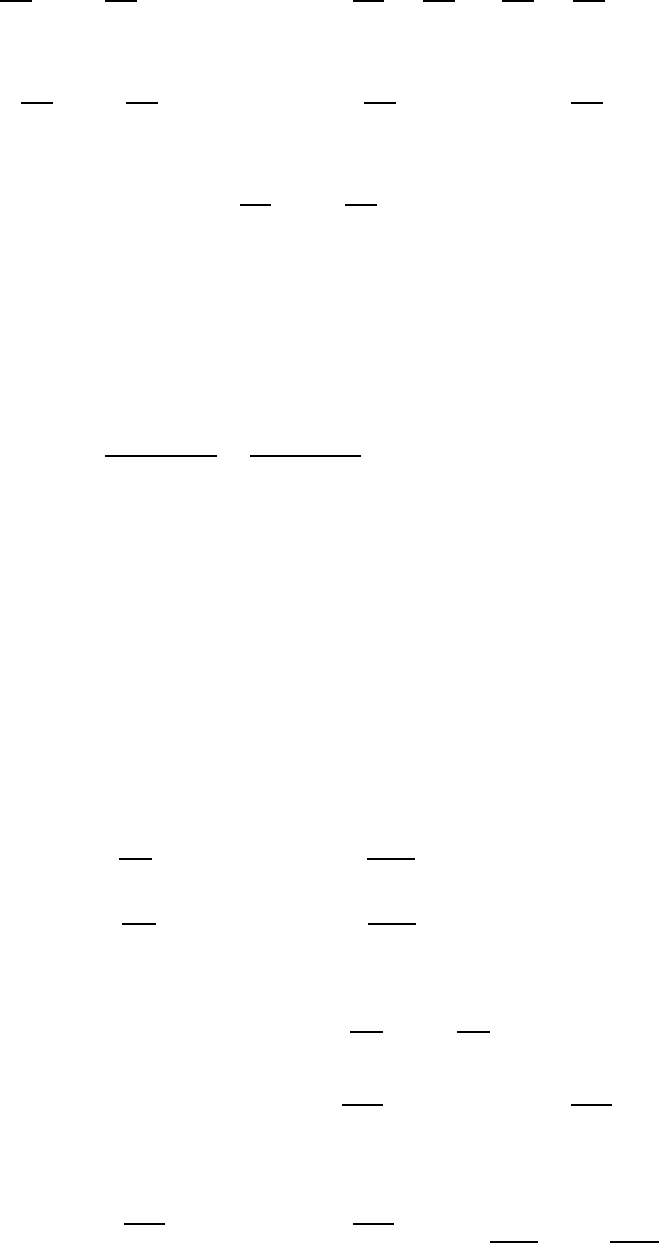
35
∫∫
((
)
(
)
)
∫∫
(
(
)
(
))
∫∫
((
)
(
)
)
∫
(
)
|
∫
(
)
|
∫∫
((
)
(
)
)
откуда следует, что . Заметим, что собственное число , так как
если , то интеграл в правой части равен нулю, откуда следует, что част-
ные производные функции равны нулю, то есть . Но
так как на границе прямоугольника , то , что невозможно.
Для решения уравнения
c граничными условиями
снова применим метод Фурье. Тогда после подстановки и
деления полученного равенства
На произведение
можно записать два уравнения:
где . Из граничных условий следует, что
Такого типа задачи Штурма-Лиувилля уже решались:
(
)
(
)
(
)
(
)
При
(
)
(
)
общее решение уравнения
имеет вид
(
√
)
(
√
)
где
и
– произвольные постоянные. Таким образом, функции
(
(
√
)
(
√
))
(
)
(
)
удовлетворяют исходному волновому уравнению с соответствующими гра-
ничными условиями. Как и ранее составим ряд:
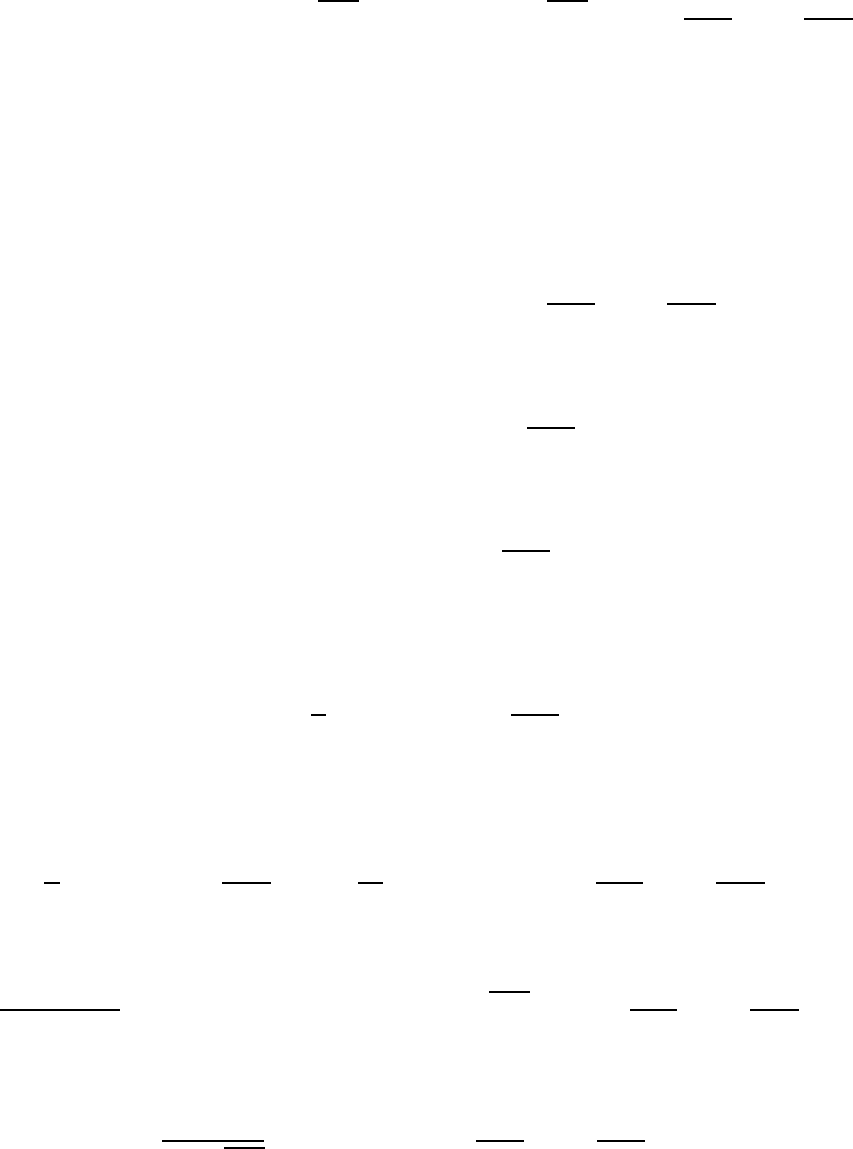
36
∑∑(
(
√
)
(
√
))
(
)
(
)
В случае равномерной сходимости этого ряда и рядов, получающихся
из него двукратным почленным дифференцированием, очевидно, сумма так-
же будет удовлетворять волновому уравнению и соответствующим гранич-
ным условиям. Подберем теперь соответствующим образом коэффициенты
и
для того, чтобы удовлетворить начальным условиям. Первое из
начальных условий дает:
∑∑
(
)
(
)
или
∑
(
)
То есть, на введенное здесь обозначение
∑
(
)
можно смотреть как на коэффициенты разложения функции
в ряд по
синусам для каждого фиксированного значения
∫
(
)
Из сопоставления двух последних равенств получаем, что
– коэффициен-
ты разложения функции
по синусам, то есть
∫
(
)
∫∫
(
)
(
)
Второе начальное условие дает:
|
∑∑
√
(
)
(
)
Рассуждения, аналогичные изложенным выше, позволяют утверждать, что
√
∫∫
(
)
(
)

37
1.20 Решение задачи о распространении тепла в стержне с однород-
ными граничными условиями методом Фурье
Рассмотрим сначала задачу о распространении тепла в стержне, концы
которого поддерживаются при нулевой температуре. Задача состоит в отыс-
кании решения уравнения теплопроводности
при граничных условиях
и при начальном условии
. Попытаемся сначала найти неравное тождественно нулю ре-
шение этого уравнения, удовлетворяющее граничным и начальным услови-
ям, причем будем искать это решение в виде
где – функция одного переменного , а – функция зависящая толь-
ко от . После подстановки разделим полученное равенство
на
. Заметим, что соотношение
должно выполняться при всех и . Так как правая часть этого
равенства зависит только от , а левая – только от , то при изменении своих
аргументов, они сохраняют постоянное значение. Обозначим это постоянное
значение через . Тогда получим
Из граничных условий
полу-
чаем
. Здесь
иначе решение
было бы тожде-
ственно равно нулю. Таким образом, для нахождения функции можно
сформулировать следующую задачу, называемую задачей Штурма-
Лиувилля: найти те значения параметра , при которых существует нетри-
виальное решение уравнения , удовлетворяющее краевым
условиям
. Те значения параметра
, при которых существу-
ет ненулевое решение этой задачи, называются собственными числами, а
сами решения – собственными функциями задачи Штурма-Лиувилля.
Для нахождения решения задачи Штурма-Лиувилля предположим сначала,
что . Тогда общее решение уравнения имеет вид:
√
√
Из граничных условий получим
,
√
√
, отку-
да следует, что
, значит и не может быть соб-
ственным числом. В случае, когда , решение этого же уравнения имеет
вид
. Из граничных условий следует, что
и зна-
чит . Следовательно, и не может быть собственным числом.
При общее решение уравнения имеет вид:
(
√
)
(
√
)
Из условия следует, что
. Из условия получаем, что
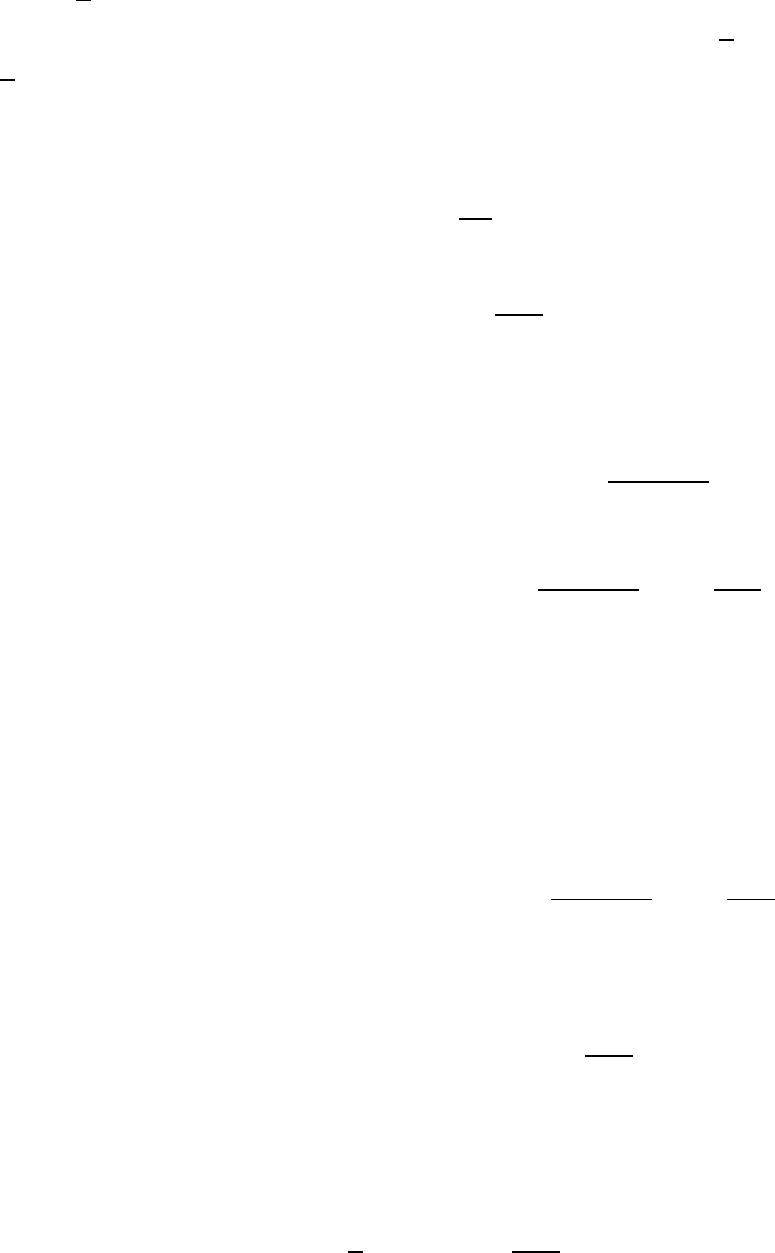
38
(
√
)
. Если
, получается тривиальное решение .
Таким образом, следует считать, что
. Тогда
(
√
)
, откуда
√
, где – любое целое положительное число.
Итак, собственные функции, соответствующие собственным числам задачи
Штурма-Лиувилля
(
)
представим в виде
(
)
где . Они определяются с точностью до произвольного множите-
ля, который выберем равным единице.
При
решение уравнения
имеет вид:
(
)
Таким образом, функции
(
)
(
)
удовлетворяют исходному уравнению теплопроводности с соответствующи-
ми граничными условиями при любых постоянных значениях
. Так как это
уравнение линейное и однородное, всякая конечная сумма решений также
будет решением этого же уравнения, удовлетворяющим граничным услови-
ям. Это же утверждение, очевидно, справедливо и для бесконечной суммы,
то есть ряда, если он сходится и его можно дважды почленно дифференциро-
вать по и один раз по . Итак, пусть
∑
∑
(
)
(
)
Осталось так подобрать коэффициенты
, чтобы удовлетворить начальному
условию:
∑
(
)
Эта формула представляет собой разложение функции
в ряд Фурье по
синусам на интервале . Коэффициенты этого разложения определяются
по формулам
∫
(
)
Покажем, что если непрерывная функция, имеющая кусочно-
непрерывную производную, причем , то ряд сходится рав-
номерно и абсолютно. Его можно почленно дифференцировать любое число
раз по и по при . В силу условий, наложенных на функцию ,
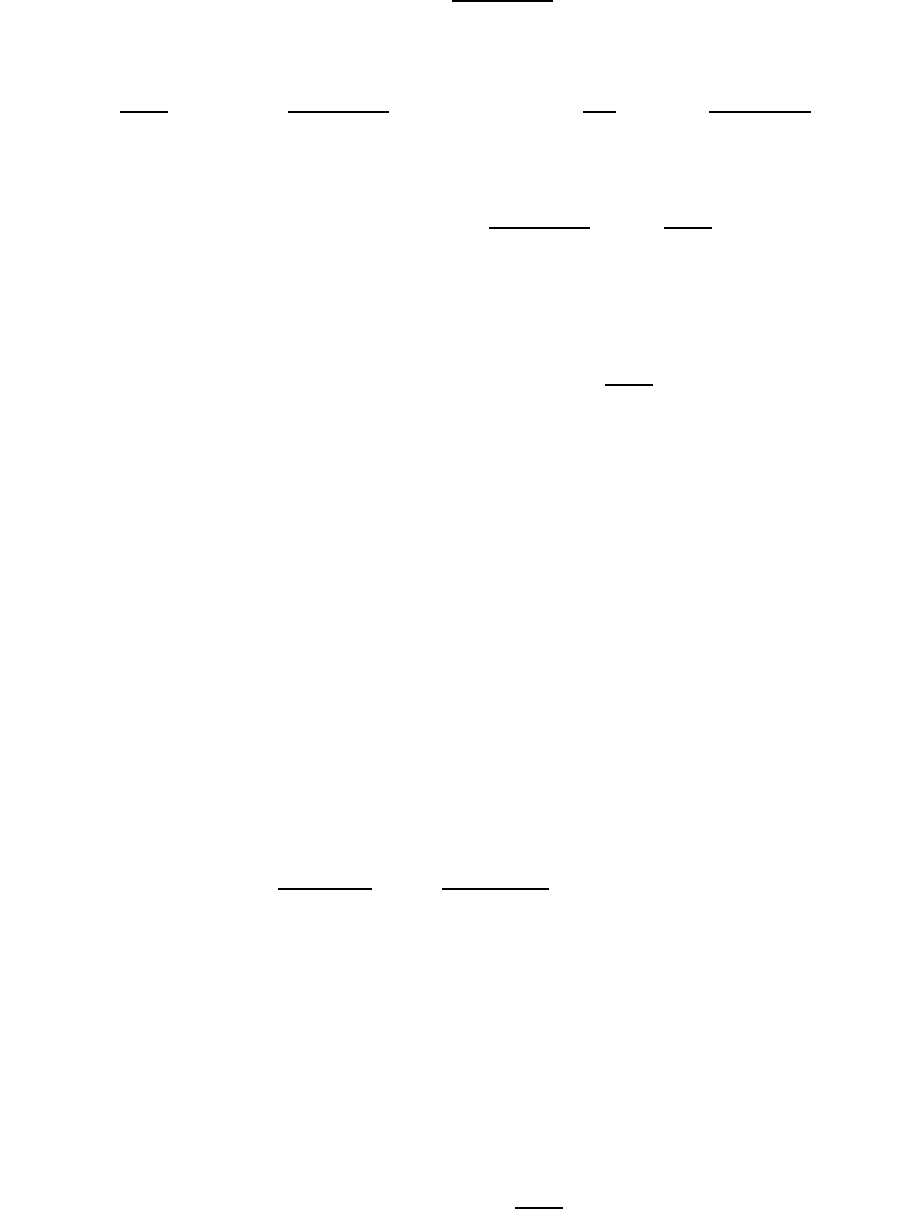
39
равномерная и абсолютная сходимость решения уравнения теплопроводно-
сти в виде ряда является следствием известной теоремы из теории тригоно-
метрических рядов. Поскольку при
(
)
а при и достаточно больших
(
)
(
)
(
)
члены ряда
∑
(
)
(
)
при и ряды, получаемые его почленным дифференцированием по или
при и больших мажорируются членами ряда
∑
(
)
Отсюда следует, что все эти ряды также сходятся абсолютно и равномерно.
Тогда из теории рядов следует, что функция
непрерывна при и
дифференцируема при , причем ряд можно дифференцировать почлен-
но. Аналогично проверяется существование производных любого порядка
при . В дальнейшем при применении метода разделения переменных
ограничимся формальной процедурой построения решения, не выясняя усло-
вий сходимости получаемых рядов.
1.21 Решение задачи о распространении тепла в стержне с неодно-
родными граничными условиями методом Фурье
Рассмотрим сначала неоднородное уравнение теплопроводности
при граничных условиях
и при начальном условии
. Решение этой задачи будем искать в виде
∑
где
– собственные функции соответствующей задачи Штурма-
Лиувилля, которая получается при решении однородного уравнения. В
нашем случае
(
)
Предположим, что функция
такова, что разлагается в ряд по функци-
ям
, то есть
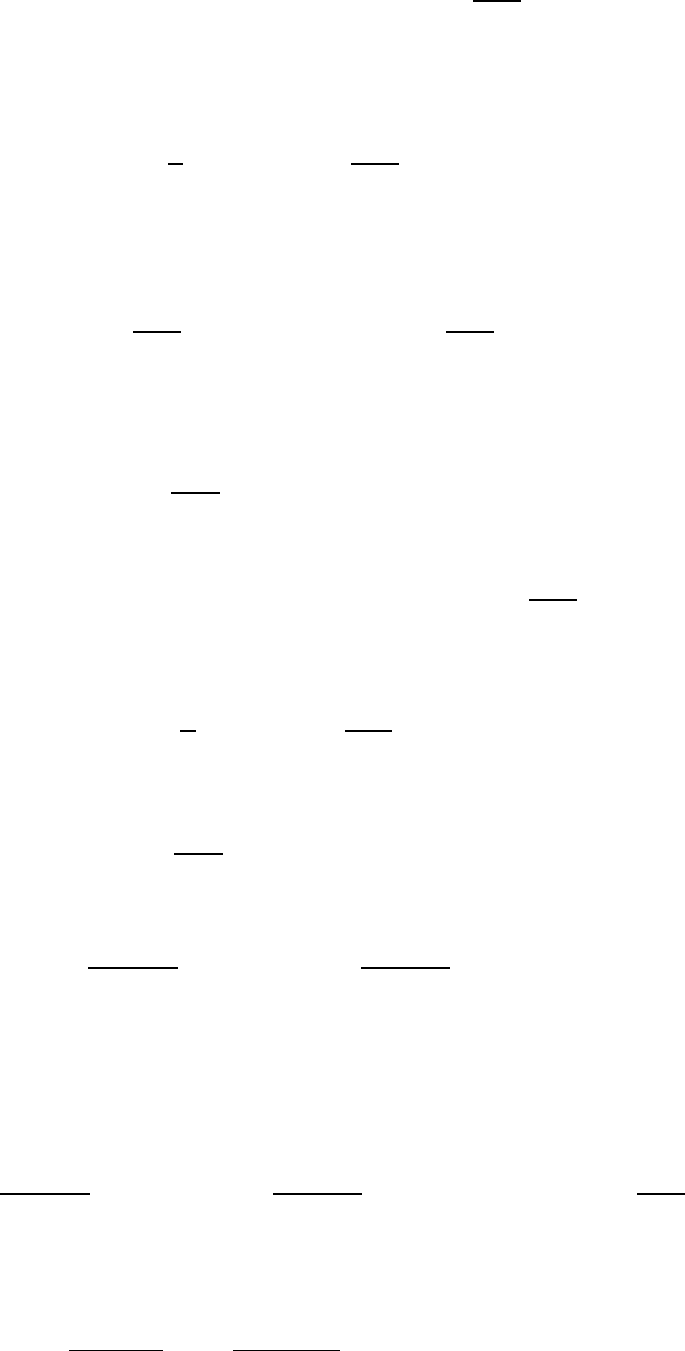
40
∑
∑
(
)
Здесь
– коэффициенты Фурье функции
, которые, как известно,
находятся по формуле
∫
(
)
Подставляя эти выражения в неоднородное уравнение теплопроводности и
полагая, что ряд можно почленно дифференцировать, получим
∑.
(
)
/
(
)
Отсюда, в силу линейной независимости функций следует, что
функции
должны удовлетворять уравнениям
(
)
Из начального условия следует
∑
∑
(
)
откуда заключаем, что
∫
(
)
Решая обыкновенные дифференциальные уравнения
(
)
с начальными условиями для
, получим:
(
)
∫
(
)
И окончательно имеем
∑
∑{
(
)
∫
(
)
}
(
)
Обобщим на случай, когда граничные условия неоднородные, то есть
требуется найти решение неоднородного уравнения теплопроводности
