Попов В.А. Математические методы моделирования физических процессов
Подождите немного. Документ загружается.

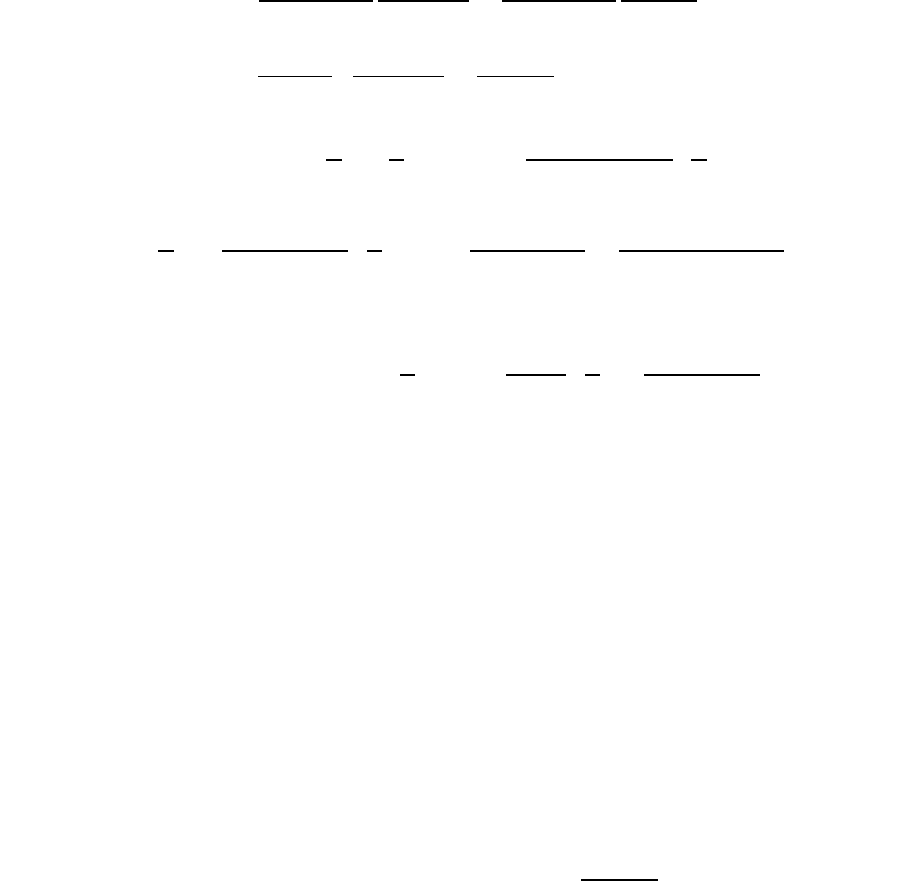
61
(
)
(
)|
(
)
∑
(
)
∑
(
)
(
)
В частности, при имеем
(
)
∑
(
)
Отметим, что
неограничена в нуле:
при
в отличие от функции
:
при
Функции
и
называют модифицированными цилиндрическими
функциями (модифицированными функциями Бесселя), соответственно
первого и второго рода порядка .
2.4 Присоединенные функции Лежандра
Любые решения уравнения Лежандра
(
)
называют присоединенными функциями Лежандра степени и порядка .
Итак, перейдѐм к нахождению нетривиальных решений этого
уравн
е
н
ия,
ограниченных
на
.
Умножив это уравнение на
, преобразуем
его
к
ф
о
р
м
е
(
)
У этого уравнения две особые точки . Эти особые точки являются
правильными. Действительно, в соответствии с определением, если в
окрестности некоторой точки линейное дифференциальное уравнение мо-
жет быть приведено к виду
где и – некоторые функции , аналитические в некоторой окрестно-
сти точки : | | , т.е. функции, которые представимы в этой -
окрестности степенными рядами
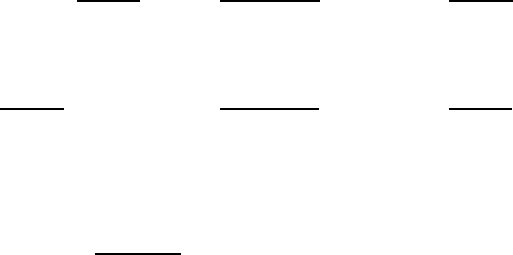
62
то точку называют правильной особой точкой этого уравнения. И в очень
малой окрестности правильной особой точки получаем уравнение
решение которого можно искать в виде
. Из соответствующего
ему характеристического уравнения
находим два корня
и
. Пусть
. Оказывается, что так же, как
и для уравнения Бесселя (для которого точка является правильной особой
точкой), при
можно всегда представить решение в виде
(
∑
)
При этом
можно взять произвольным, а коэффициенты
при
определяются уже однозначно, и степенной ряд в представлении
сходится в некоторой достаточно малой окрестности точки . Что каса-
ется решения
, отвечающего второму корню при
характеристиче-
ского уравнения, то тут ситуация несколько более сложная. Если
целому числу, то существует и второе решение
, формально такого же
вида, как и
:
(
∑
)
Если же
целому числу, не равному нулю, то существует решение
такого же вида. В случае же, когда
, второе решение, линейно незави-
симое с
, имеет в малой окрестности точки поведение вида:
Вернемся теперь к уравнению Лежандра в форме
(
)
имеющего две особые точки и . Покажем, что эти точки явля-
ются правильными, например, для точки . Для этого разделим по-
следнюю форму записи уравнения Лежандра на функцию
, которая
не обращается в нуль в окрестности исследуемой точки . Уравнение
приобретает вид
(
)
С этом случае и функции
являются регулярными в круге
|
|
, где уже как комплексная пере-
менная, то есть представимы в этой области степенными рядами.
∑
∑
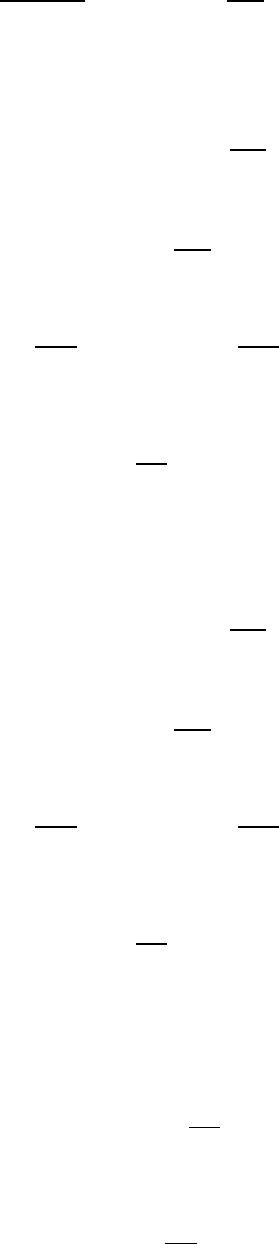
63
∑
∑
Итак, точка является правильной. Таким образом, решение уравнения
Лежандра при
можно искать в виде
с характеристическим уравнением
корни которого равны
|
|
|
|
Тогда всякое ограниченное в окрестности точки решение уравнения
Лежандра имеет вид
|
|
где функция
аналитическая, а потому и бесконечное число раз диф-
ференцируемая функция в окрестности точки .
Аналогичным образом решение уравнения Лежандра при
можно искать в виде
с характеристическим уравнением
корни которого оказываются в точности теми же
|
|
|
|
Тогда всякое ограниченное в окрестности точки решение уравнения
Лежандра имеет вид
|
|
где функция
аналитическая, а потому и бесконечное число раз диф-
ференцируемая функция в окрестности точки .
Отсюда уже следует, что если
– решение уравнения Лежандра, то
функция
|
|
должна быть бесконечное число раз дифференцируема в области
[
]
. В
самом деле, в окрестностях точек функция
|
|
бесконечное число раз дифференцируема, поскольку таковыми являются в
этих окрестностях функции
и
|
|
. Таким образом, прихо-
дим к заключению, что решение
уравнения Лежандра, ограниченное на
[
]
, следует искать в виде

64
|
|
где
– бесконечное число раз дифференцируемая функция в области
[
]
. Подставляя это соотношение в исходное уравнение Лагранжа, при-
ходим к приходим к следующему уравнению для отыскания функции
:
|
|
(
|
| |
|
)
Далее требуется найти нетривиальное решение
этого уравнения, огра-
ниченное и бесконечное число раз дифференцируемое на промежутке
[
]
.
Установим, что такими решениями будут некоторые многочлены, и найдѐм
их. Для этого рассмотрим несколько более общее семейство уравнений, зави-
сящее от действительного параметра n:
(
)
по форме записи совпадающее с предыдущим уравнением при
|
|
. От-
метим, что если
– решение этого уравнения, то
является решением
этого же уравнения, но с значением , на единицу большем. При это
уравнение преобразуется к виду
решение которого эквивалентно решению уравнения первого порядка
Но последнее уравнение легко интегрируется, как уравнение с разделяющи-
мися переменными. Одним из решений этого уравнения является функция
Опираясь на эти свойства, найдем
. Чтобы получить решение при
, достаточно раз продифференцировать многочлен
, и
полученный многочлен будет с точностью до постоянного множителя един-
ственным нетривиальным ограниченным на промежутке
[
]
решением:
Вместо такого многочлена берут многочлен с нормировочным множителем
выбранным из условия
. Систему многочленов
,
называют системой многочленов Лежандра, а полученная формула для их
вычисления носит название формулы Родрига для многочленов Лежандра.
При
|
|
единственным решением, ограниченным на промежутке
[
]
,
является многочлен
|
|
|
|
Отметим, что при
|
|
этот многочлен будет равен тождественно нулю.
Окончательно, нетривиальным ограниченным на интервале решением
уравнения Лежандра является функция
|
|
|
|
|
|
|
|

65
где
– многочлен Лежандра степени . При этом такие нетривиальные
решения уравнения Лежандра существуют только для , удовлетворяющих
условию | | . При | | функции
|
|
называются присоединнны-
ми функциями Лежандра. При имеем многочлены Лежандра
.
2.5 Сферические функции
Решение уравнения Лапласа в сферических координатах
*
(
)
(
)
+
методом разделения переменных мы искали в виде произведения трех функ-
ций:
. Нахождение таких решений оказалось связано с
отысканием собственных функций и собственных значений трех обыкновен-
ных дифференциальных уравнений. Первое из них мы представили в виде:
где
– некоторая постоянная. Второе уравнение:
где
– некоторая постоянная. Третье уравнение после замены пере-
менной на преобразовали к так называемому уравнению Ле-
жандра:
(
)
Во всех важных приложениях и являются действительными целыми чис-
лами, такими, что и . Решения этого уравнения
называют присоединенными функциями Лежандра первого рода степени
и порядка :
|
|
|
|
|
|
|
|
где
– многочлен Лежандра степени .
Сферическими функциями
называют любые решения
сферического уравнения Лапласа:
(
)
Поиск частных решений этого уравнения методом разделения переменных в
виде произведения двух функций:
приводит к соот-
ношению
Это уравнение после деления на и умножения на
допускает разде-
ление переменных.

66
(
)
Здесь
– некоторая постоянная. Отсюда имеем два уравнения. Первое из
них
допускает частные решения
Второе:
– после деления на
и последующей замены переменной на
приводит к уравнению Лежандра:
(
)
Если потребовать, чтобы решения были регулярны (представимы степенным
рядом) при , и непрерывны на сфере, то мы прихо-
дим к проблеме собственных значений, допускающей решения только при
целых значениях и , таких, что и .
Собственные функции уравнения Лежандра, полученные в предыдущем па-
раграфе, называют присоединенными функциями Лежандра степени и
порядка :
|
|
|
|
|
|
|
|
где
– многочлен Лежандра степени . Таким образом, частные реше-
ния сферического уравнения Лапласа можно представить в виде:
|
|
√
|
|
|
|
|
|
Они образуют ортонормированную последовательность. Нетрудно убедиться
непосредственным вычислением, что сферические функции являются норми-
рованными:
∫
∫
и ортогональными:
∫
∫
если
или
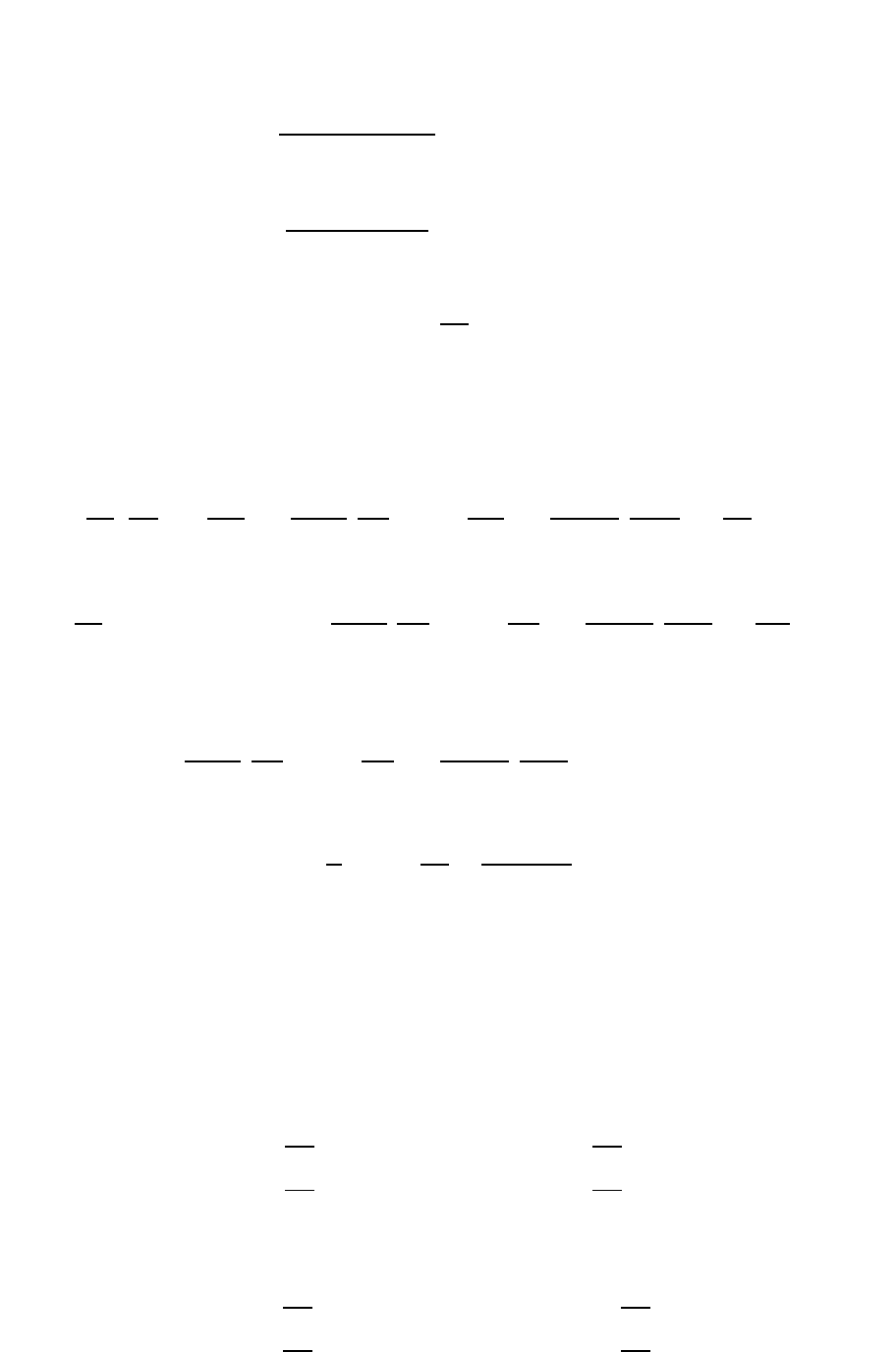
67
2.6 Сферические функции Бесселя
При разделении переменных в трехмерном волновом уравнении
и в уравнении теплопроводности
приходим к проблеме собственных значений для уравнения Гельмгольца:
Частные решения этого уравнения в сферических координатах будем
искать также методом разделения переменных. Для этого представление
– в виде произведения радиальной функции на угловую
функцию
подставим в уравнение Гельмгольца
*
(
)
(
)
+
Получим уравнение
*
(
)
+
допускающее разделение на два уравнения. Одно из них, хорошо известное
из предыдущего параграфа, называется сферическим уравнением Лапласа:
(
)
другое
(
)
при помощи замены
, где , сводится к уравнению Бесселя
Здесь введено обозначение . Решениями хорошо известного
уравнения Бесселя являются функции Бесселя первого и второго рода
,
, а также функции Ханкеля первого и второго рода
,
с полуцелыми индексами. Их называют сферическими функциями
Бесселя первого и второго рода
√
√
и, соответственно, сферическими функциями Ханкеля первого и второго
рода
√
√
68

69
3 Интегральные преобразования
3.1 Операторный метод решения линейных задач
Операторный метод – один из методов решения математических задач
путем замены изучаемых функций-оригиналов некоторыми другими функци-
ями-изображениями, получаемыми по определенным правилам.
Весьма плодотворной оказалась ранее рассмотренная идея решения
дифференциальных уравнений в частных производных путем уменьшения
числа аргументов, например, методом разделения переменных. Добиться
уменьшения числа аргументов дифференциальных уравнений в частных про-
изводных можно и с помощью интегральных преобразований. Рассмотрим
способ построения интегрального преобразования на примере сведения
обыкновенного линейного дифференциального уравнения с постоянными ко-
эффициентами к алгебраическому уравнению.
Пусть необходимо решить задачу Коши:
где
,
–заданные числа,
–известная
функция,
–искомая функция. Воспользуемся интегральным преобра-
зованием
∫
которое ставит в соответствие функции
– оригиналу другую функцию
– изображение оригинала
. В нем
– известная функция дей-
ствительного аргумента и комплексного параметра , называемая ядром
преобразования. Нижний предел интегрирования соответствует начальному
значению . Верхний предел должен соответствовать максимально допу-
стимому значению аргумента искомой функции из области ее определения.
Пусть таким значением будет . Применим данное интегральное преоб-
разование к производной
. Получим
∫
Здесь
– изображение производной
. Если применим данное ин-
тегральное преобразование к исходному дифференциальному уравнению, то
получим
Где
– изображение функции
, представленное в виде:
∫
70
Далее выберем ядро таким, чтобы изображения производных
можно выразить через изображение искомой функции. Например, для
,
применяя метод интегрирования по частям, можно получить
∫
|
|
∫
Ядро
подчиним условию
, где
– произ-
вольная функция. Тогда
|
|
а структура ядра определится результатом интегрированияобыкновенного
дифференциального уравнения первого порядка:
Отсюда следует, что
и наличие у ядра произвольного множителя
оказывается несуществен-
ным. Пусть
. Тогда при
существенно упрощается соотношение
|
|
связывающее изображение
с изображением
. Для первого слагае-
мого в правой части этого равенства потребуем
|
|
Более того, должна быть обеспечена сходимость несобственного интеграла:
∫
Пусть
е Тогда выражение под зна-
ком предела можно представить в следующем виде
|
|
поскольку
|
|
Чтобы требуемый предел выполнялся, функция
должна возрастать не
быстрее экспоненты:
|
|
