Попов В.А. Математические методы моделирования физических процессов
Подождите немного. Документ загружается.


21
Если же процесс стационарен, то есть устанавливается не меняющееся
со временем распределение температуры, то приходим к уравнению Пуас-
сона:
А при отсутствии источников тепла приходим к уравнению Лапласа:
Уравнение Пуассона, или уравнение Лапласа решаются с граничными усло-
виями первого, второго, третьего, или четвертого рода, изложенными выше.
1.11 Потенциал поля, созданного стационарным током
Пусть в проводящей среде имеется электрический ток – упорядочен-
ное движение заряженных частиц. Количественно электрический ток харак-
теризуется скалярной величиной силой тока, по определению равной отно-
шению заряда , переносимому через сечение проводника за интервал вре-
мени , к этому интервалу : , или в пределе при имеем
Электрический ток можно характеризовать и векторной величиной плотно-
стью электрического тока, по модулю равной электрическому заряду, про-
ходящему за единицу времени через единичную площадку, перпендикуляр-
ную направлению упорядоченного движения заряженных частиц
, по направлению совпадающей с направлением движения поло-
жительно заряженных частиц. Сопоставляя эти два определения, можно за-
писать выражение для силы тока через любую поверхность в виде:
∬
где для любого элемента с площадью поверхности и с векто-
ром единичной нормали к этому элементу, равным . Выберем в качестве
поверхности произвольную замкнутую поверхность, охватывающую объем
среды, по которой течет ток. Тогда в соответствии с теоремой о диверген-
ции можно перейти от интегрирования по замкнутой поверхности по объе-
му , охватываемому этой поверхностью:
∯
∭
C другой стороны, силу тока можно записать в виде:
∭
∭
Здесь использовано определение плотности заряда . А знак минус
указывает на то, что при положительном токе, направленном из объема по

22
внешней нормали , заряд в этом объеме убывает:
. И наоборот,
при отрицательном токе, направленном внутрь объема против внешней
нормали , заряд в этом объеме возрастает:
. Поскольку левые
части равенств для токов равны, должны быть равны и правые части:
∭
∭
В силу произвольности объема это равенство должно выполняться при
условии равенства подынтегральных функций:
Полученное уравнение называют уравнением непрерывности (неразрывно-
сти). Воспользуемся далее законом Ома в дифференциальной форме:
согласно которому плотность электрического тока пропорциональна
напряженности электрического поля , связанной с потенциалом соотно-
шением: . Эта связь позволяет представить закон Ома в виде:
Коэффициент пропорциональности называют удельной электрической
проводимостью. Преобразуем уравнение непрерывности, используя послед-
нюю форму записи закона Ома. Получим
Пусть в однородной среде без источников тока с постоянной удельной элек-
трической проводимостью течет стационарный ток. Тогда
Это означает, что в однородной среде без источников потенциал поля, со-
зданного стационарным током, описывается уравнением Лапласа. Уравне-
ние Пуассона, или уравнение Лапласа решаются с граничными условиями
первого, второго, третьего, или четвертого рода, изложенными выше.
1.12 Потенциал электростатического поля зарядов
Для описания электрического поля в среде воспользуемся уравнением
Максвелла
∯
∭
обобщающим закон Кулона. Оно, в соответствии с теоремой Остроградского-
Гаусса для электрических полей в среде, утверждает, что поток вектора элек-
трической индукции через любую замкнутую поверхность равен заряду в
объеме , охватываемому этой поверхностью. С помощью материального
уравнения
, отражающего определение диэлектрической проницае-

23
мости среды , перейдем от вектора электрической индукции к вектору
электрической напряженности .
∯
∭
Здесь
– электрическая постоянная, связанная с выбором системы единиц, в
нашем случае системы СИ. В соответствии с теоремой о дивергенции в левой
части этого равенства можно перейти от интегрирования по замкнутой по-
верхности по объему , охватываемому этой поверхностью:
∯
∭
В силу произвольности объема полученное равенство
∭
∭
должно выполняться при условии равенства подынтегральных функций:
Воспользуемся соотношением , связывающим напряженность
электрического поля с потенциалом . Тогда
В случае однородной среды с диэлектрической проницаемостью
получим уравнение Пуассона:
Если внутри рассматриваемой области нет объемных зарядов, получим
уравнение Лапласа:
Уравнение Пуассона, или уравнение Лапласа решаются с граничными усло-
виями первого, второго, третьего, или четвертого рода, изложенными выше.
1.13 Канонический вид уравнений в частных производных второго
порядка
Начнем с понятия дифференциального уравнения в частных производ-
ных. Пусть – область -мерного евклидового пространства
, где ;
. Пусть, далее
– заданная
функция точек и переменных
с неотрицательными целочисленными
индексами
, такими, что
, ; ,
причем, по крайней мере одна из частных производных
для набора индексов, удовлетворяющих условию
, отлична
от нуля. Тогда уравнение

24
(
)
называется дифференциальным уравнением с частными производными
порядка относительно неизвестной функции . Левая часть этого равен-
ства представляет собой дифференциальный оператор с частными производ-
ными, действующий на гладкую функцию . Порядком дифференциально-
го уравнения с частными производными называется порядок наивысшей
производной, входящей в уравнение. В том случае, когда
– -
мерные вектора, то пространство этих векторов называется системой
дифференциальных уравнений с частными производными порядка
относительно неизвестных функции
. Функция (набор функций), ко-
торая при подстановке в уравнение (систему уравнений) обращает его в тож-
дество, называется решением уравнения (системы уравнений). В том случае,
когда линейно зависит от функции и ее производных, уравнение называ-
ется линейным. В общем виде линейное уравнение может быть записано в
виде , где – линейный оператор. Линейное уравнение называют од-
нородным, если и неоднородным в противном случае. Если диффе-
ренциальное уравнение не является линейным, его называют нелинейным.
Среди нелинейных уравнений выделяют квазилинейные уравнения. Уравне-
ние или систему уравнений называют квазилинейной, если она линейна от-
носительно всех старших производных от неизвестных функций.
В примерах, приведенных выше, уравнение теплопроводности, уравне-
ние Пуассона и волновое уравнение являются линейными уравнениями вто-
рого порядка. Система телеграфных уравнений является линейной системой
уравнений первого порядка. Система уравнений гидродинамики – это пример
квазилинейной системы уравнений первого порядка.
Классификация уравнений с частными производными второго порядка
тесно связана с преобразованием уравнений к определенному виду, называе-
мому каноническим. Уравнение, записанное в каноническом виде, как пра-
вило, проще исследовать, в некоторых случаях они поддаются аналитиче-
скому решению. Линейное уравнение второго порядка можно представить в
виде:
∑∑
∑
где
,
, , – заданные функции, вообще говоря, зависящие от
переменных
. Оно называется однородным, если , и неодно-
родным в противном случае.
Упростим часть уравнения, которая содержит вторые производные не-
известной функции. Но, прежде чем это делать изучим, как изменяются ко-
эффициенты при произвольной замене переменных. Введем вместо перемен-
ных
новые переменные
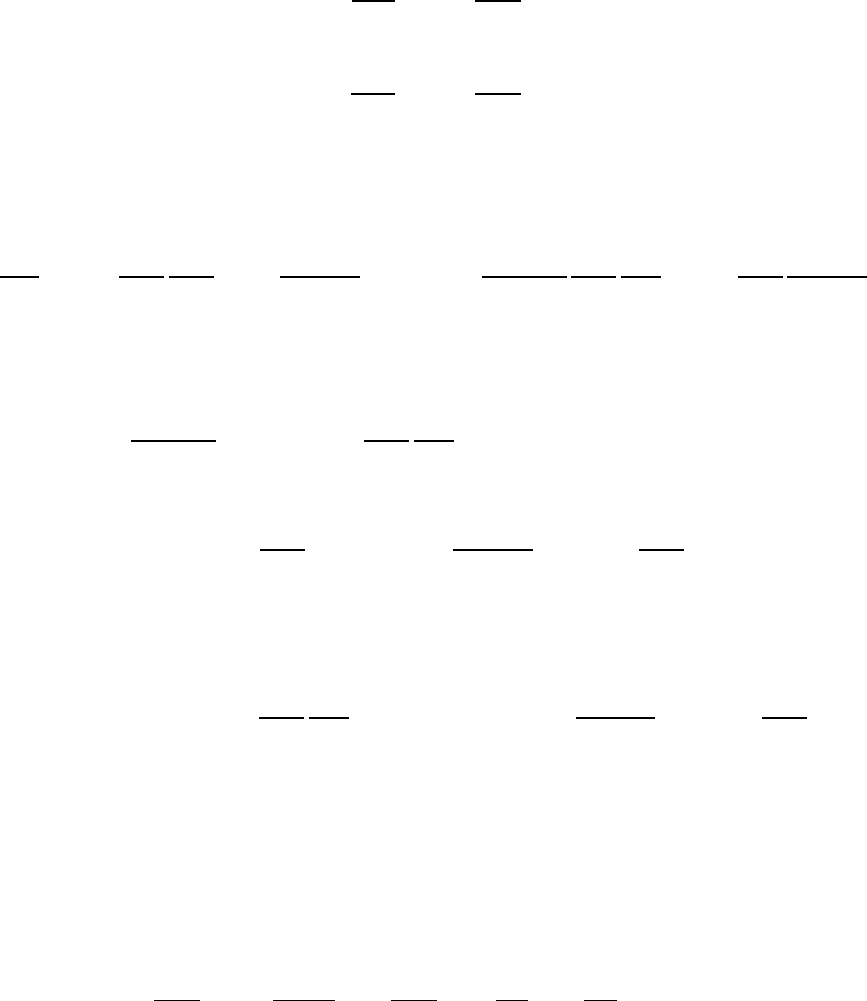
25
Допустим, что эти функции обладают вторыми производными и замена пе-
ременных невырожденная в окрестности некоторой точки
, то есть
в окрестности этой точки якобиан
|
|
|
|
отличен от нуля. Тогда, если
(
)
то
∑
∑∑
∑
Подставляя эти выражения в исходное линейное уравнение второго порядка
и меняя порядок суммирования, получим:
∑∑
.∑∑
/
∑
.∑∑
∑
/
В этом уравнении обозначим через
̃
коэффициенты при вторых производ-
ных, а через
̃
коэффициенты при первых производных:
̃
∑∑
̃
∑∑
∑
В случае, когда функции зависят от
независимых переменных, в каждой
фиксированной точке пространства можно подобрать свое преобразование
так, чтобы уравнение не содержало смешанных производных. Покажем, что
если , то можно так подобрать такое преобразование, что уравнение
приведется в некоторой области к специальному виду, называемому канони-
ческим. Для этого рассмотрим уравнение
где – функции от , причем одновременно в нyль не
обращаются. Этому уравнению соответствует квадратичная форма
В курсе аналитической геометрии такие формы путем замены переменных
упрощались, они приводились к каноническому виду и им соответствовали
кривые второго порядка:
если
– гипербола;
если
– парабола;
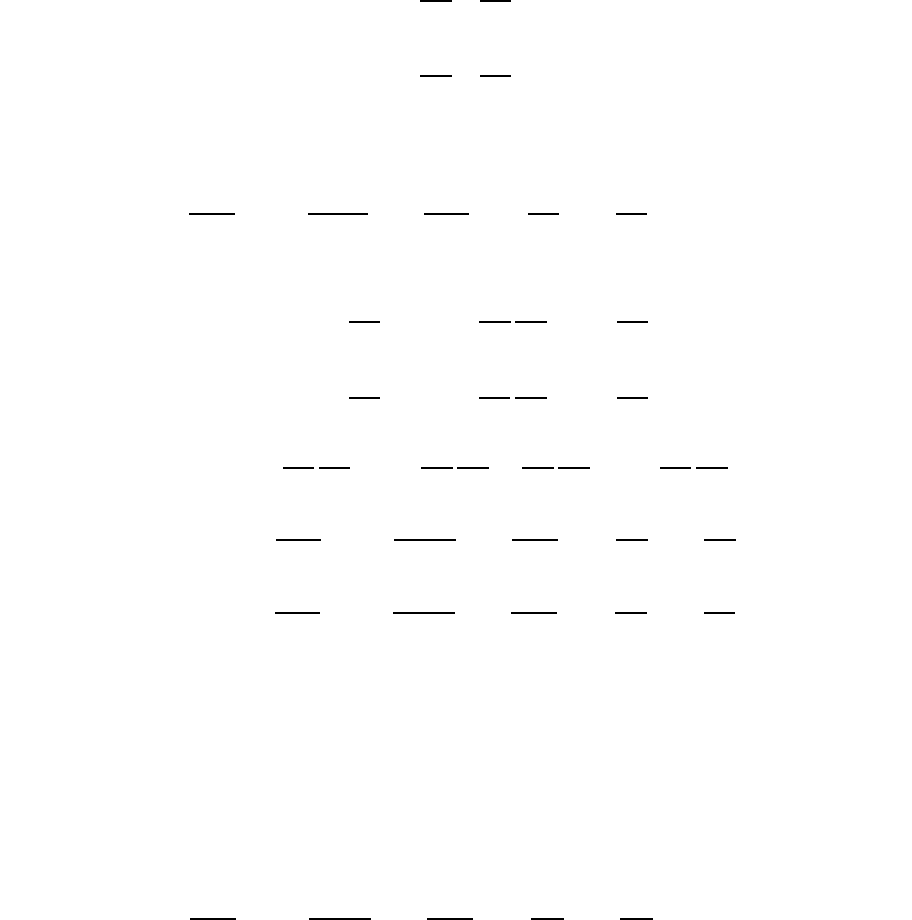
26
если
– эллипс.
Покажем, что вид рассматриваемого уравнения можно упростить. По-
лученный вид будем называть каноническим и он зависит от знака выраже-
ния
. По аналогии с аналитической геометрией при
уравнение будем называть гиперболическим, при
– парабо-
лическим и при
– – эллиптическим.
Введем переменные , , причем так, чтобы заме-
на была невырожденной, то есть определитель
|
|
|
|
в окрестности некоторой фиксированной точки
. В новых переменных
уравнение перепишется в виде
̃
̃
̃
̃
̃
̃
̃
где
̃
(
)
(
)
̃
(
)
(
)
̃
(
)
̃
̃
Легко видеть, что
(
̃
–
̃
̃
)
(
–
)
, следовательно, преобразование
не меняет тип уравнения.
1.14 Канонический вид уравнения гиперболического типа
Пусть рассматриваемое уравнение
является уравнением гиперболического типа, для которого
.
Покажем, что можно так подобрать функции , , что в окрестно-
сти точки
будут выполнены равенства . Предположим,
что либо , либо не равны 0, так как в противном случае требуемый вид
уже получен. Пусть, например, . Тогда, так как
, урав-
нение
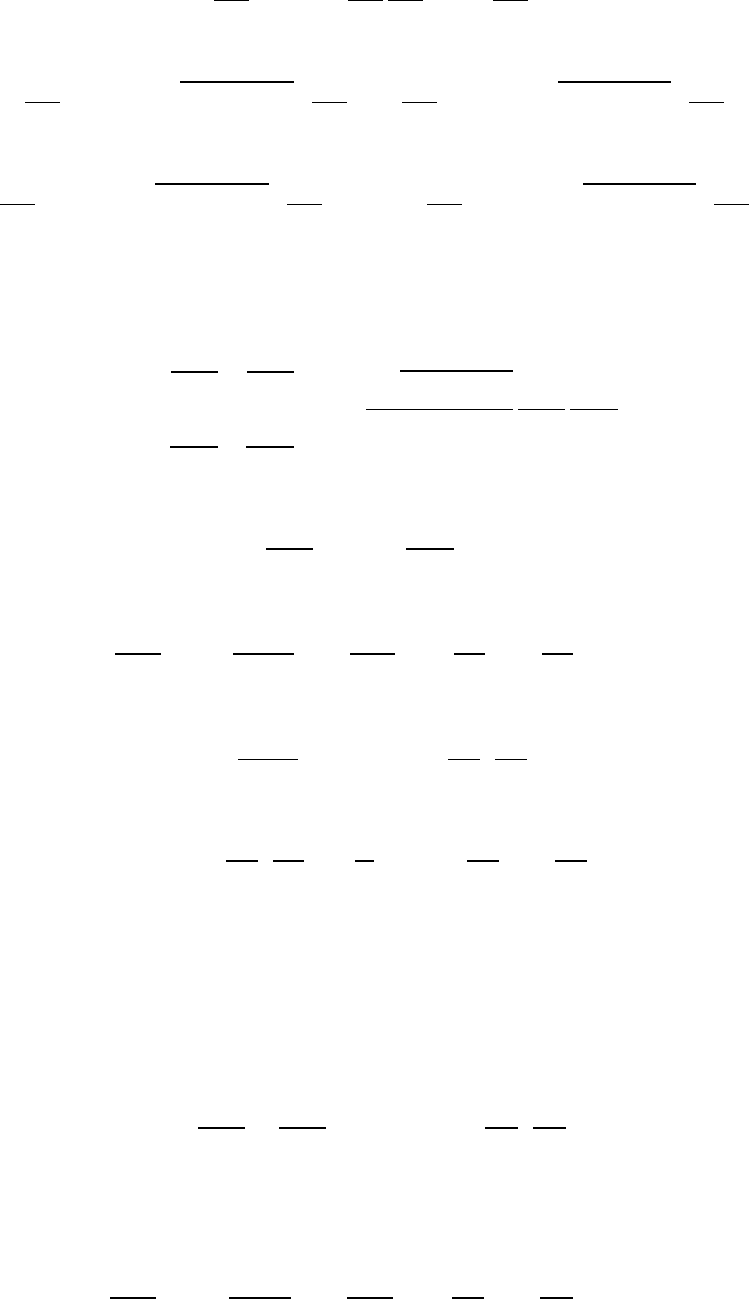
27
(
)
(
)
представимо в виде
(
(
√
)
)(
(
√
)
)
которое, в свою очередь, распадается на два:
(
√
)
(
√
)
Пусть
,
– решения этих уравнений. Эти решения
можно выбрать так, чтобы в окрестности точки
функции
и
бы-
ли независимыми. Действительно, так как , то из уравнений имеем
|
|
|
|
√
Это означает, что достаточно выбрать такие решения, чтобы
Итак, произведя замену
,
, получим, что уравнение
̃
̃
̃
̃
̃
̃
̃
примет вид
̃
(
)
где
̃
(
)
̃
(
̃
̃
̃
)
Такой вид принято называть вторым каноническим видом для уравнения
гиперболического типа. В записи канонического вида специально выделили
часть уравнения, содержащую вторые производные, и записали в общем виде
все остальные слагаемые, чтобы подчеркнуть, что канонический вид харак-
теризуется только вторыми производными. Если теперь выполнить еще одну
замену , , то получим
(
)
Это и есть канонический вид для уравнения гиперболического типа.
Кривые
,
называют характеристическими кри-
выми или кратко характеристиками рассматриваемого уравнения:
Вдоль них выполняются соответственно равенства , .

28
1.15 Канонический вид уравнения параболического типа
Пусть рассматриваемое уравнение
является уравнением параболического типа, для которого
. То-
гда уравнения
(
√
)
(
√
)
вырождаются в одно уравнение:
Заметим, что из условия
следует равенство . Зна-
чит, существует такое , что , . Следовательно, функция
удовлетворяет и уравнению
Пусть , где – решение этого уравнения, – любая гладкая
функция, такая, что
|
|
|
|
В уравнении
̃
̃
̃
̃
̃
̃
̃
коэффициенты
̃
̃
(
)
(
)
Заметим, что , так как в противном случае функция удо-
влетворяет тому же уравнению, что и функция , а это в свою оче-
редь противоречит условию невырожденности замены переменных. Следова-
тельно, в окрестности точки
имеем
̃
(
)
Это и есть канонический вид уравнения параболического типа. В рас-
сматриваемом случае кривые называются характеристиками
уравнения:
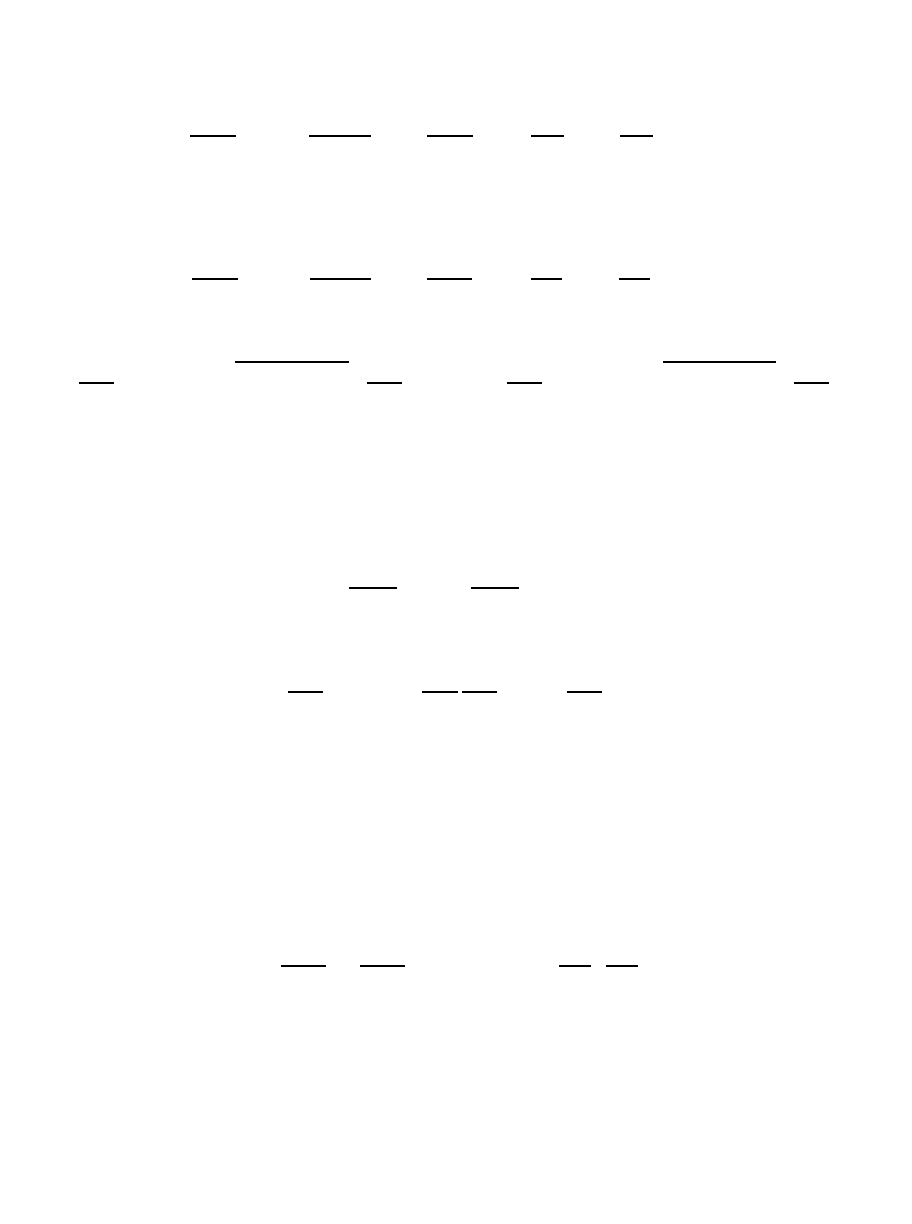
29
1.16 Канонический вид уравнения эллиптического типа
Пусть рассматриваемое уравнение
является уравнением эллиптического типа, для которого
– . По-
кажем, что можно так подобрать функции и , чтобы в уравнении
̃
̃
̃
̃
̃
̃
̃
коэффициенты
̃
̃
,
̃
. Заметим, что в уравнениях
(
√
)
(
√
)
коэффициенты являются комплексно-сопряженными. Тогда решения этих
уравнений также могут быть выбраны комплексно-сопряженными. Пусть
– решение одного из этих уравнений, причем такое,
что
(
)
(
)
Пусть
,
. Тогда, так как – решение уравнения
(
)
(
)
то обращает его в тождество с комплекснозначной функцией в левой части.
Следовательно, ее действительная и мнимая части тождественно равны ну-
лю. Выражая эти действительные и мнимые части и приравнивая их нулю,
получим после простых преобразований
̃
̃
,
̃
. Так как
̃
̃
(в
противном случае
̃
–
̃
̃
), то в новых переменных уравнение примет
вид:
(
)
Это и есть канонический вид уравнения эллиптического типа.
Заметим, что гиперболические уравнения имеют два семейства дей-
ствительных характеристик, параболические – одно, а эллиптические урав-
нения действительных характеристик не имеют.
1.17 Корректность постановки задач математической физики
Постановка задач математической физики содержит помимо диффе-
ренциальных уравнений или систем некоторые дополнительные функции,
назовем их входными условиями. Этими условиями являются, например,
значения решения на некоторых кривых, поверхностях, которые задают для
однозначного определения решения. Значения входных условий находятся из
30
опыта и поэтому неизбежна некоторая погрешность в их определении. Эта
погрешность будет сказываться на решении, и не всегда погрешность в ре-
шении будет мала. Будем говорить, что задача поставлена корректно, если
она разрешима при любых входных данных, принадлежащих некоторому
классу, имеет единственное решение и это решение непрерывно зависит от
входных данных. Последнее означает, что в пространствах входных данных и
решений можно ввести расстояния, причем для любого существует
такое, что если входные данные отличаются не более чем на , то со-
ответствующие им решения отличаются не более чем на . Это свойство ча-
сто называют устойчивостью.
Задача поставлена некорректно, если она разрешима не при любых
начальных данных из некоторого класса, либо имеет не единственное реше-
ние, либо нельзя выбрать такие расстояния, чтобы в них была непрерывная
зависимость от входных данных.
В дальнейшем нас, прежде всего, будет интересовать вопрос о кор-
ректности постановки той или иной задачи для различных типов уравнений и
систем. При постановке задачи необходимо убедиться в том, что
1) дополнительные условия не переопределяют задачу, то есть среди них
нет несовместных условий – достигается доказательством теоремы суще-
ствования, которое обычно связано с методом решения;
2) дополнительных условий достаточно для выделения однозначного ре-
шения – достигается доказательством теоремы единственности;
3) решение непрерывно зависит от начальных данных.
Если хотя бы одно условие нарушено, то задача будет некорректной. В
настоящее время для решения некорректных задач разработаны свои методы.
В классических же методах математической физики рассматриваются в ос-
новном корректно поставленные задачи.
1.18 Решение задачи о свободных колебаниях струны методом Фурье
Рассмотрим задачу о свободных колебаниях струны длиной . Задача
состоит в отыскании решения волнового уравнения
с закрепленными концами
при начальных условиях:
|
Будем искать частные решения, не равные тождественно нулю, в виде произ-
ведения
