Попов В.А. Математические методы моделирования физических процессов
Подождите немного. Документ загружается.


41
удовлетворяющее граничным и начальным условиям:
Эта задача легко сводится к предыдущей задаче с однородными граничными
условиями в случае гладких функций
и
. Действительно, введем
новую функцию
такую, что
. Гладкую функ-
цию
подберем так, чтобы она удовлетворяла тем же граничным усло-
виям, что и функция
. Таких функций существует бесконечно много. В
частности, можно взять
(
–
)
Тогда для функции
получается следующая задача: найти решение не-
однородного уравнения теплопроводности
(
)
удовлетворяющее однородным граничным условиям
и начальному условию
Решение этой задачи с известной функцией, стоящей в скобках правой части
неоднородного уравнения теплопроводности, рассмотрено в начале настоя-
щего параграфа.
1.22 Решение задачи Коши для уравнения теплопроводности
Рассмотрим задачу Коши для уравнения теплопроводности
с начальным условием
, где
– ограниченная функция. Для
простоты рассмотрим случай . Все рассуждения, приведенные ниже,
справедливы и для произвольного . Убедимся в том, что функция
√
∫
(
)
при всех
и удовлетворяет уравнению
Введем функцию
{
√
(
)
при
при
называемую функцией Грина (функцией источника). Тогда
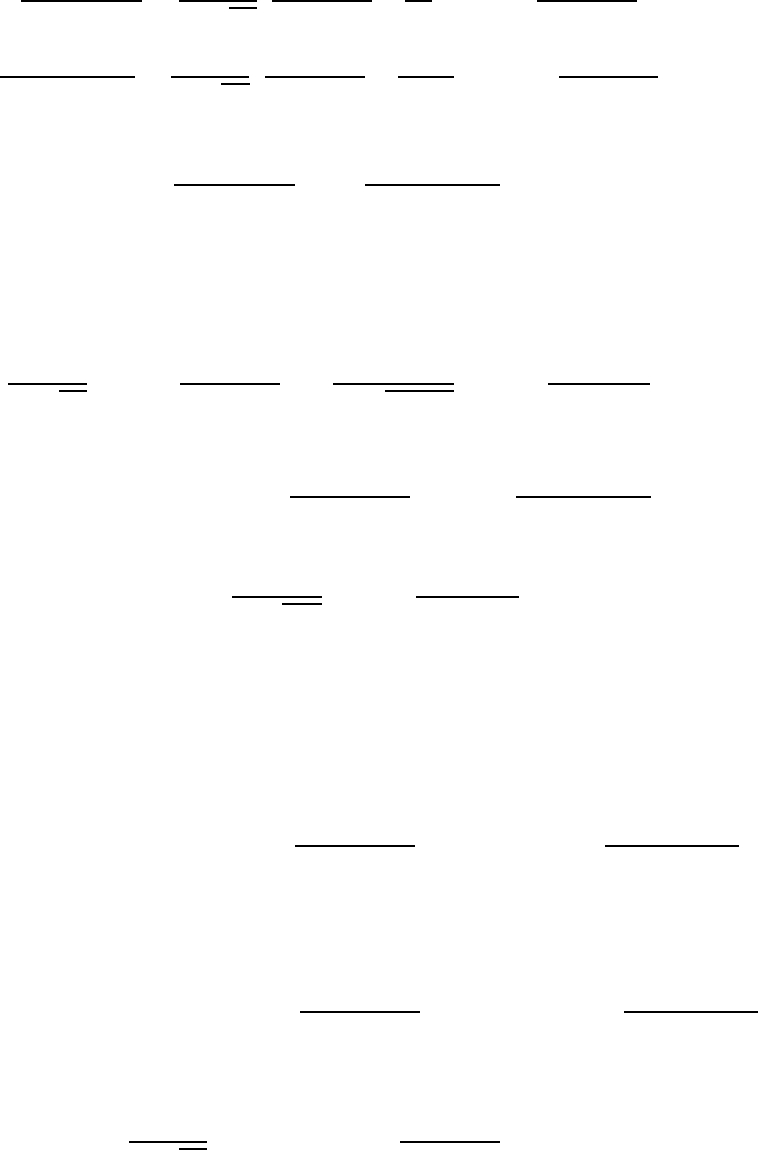
42
∫
Подставляя в уравнение теплопроводности производные
√
*
+
(
)
√
*
+
(
)
нетрудно убедиться в том, что
По условию функция
ограничена, т. е. существует такое, что при
всех
выполняется неравенство
|
|
. Кроме того, для всех та-
ких, что
|
|
и всех таких, что
, имеем
|
|
|
|
при
любых и
√
(
)
√
(
)
Тогда функции
мажорируются функцией
√
(
)
для которой интеграл
∫
сходится, следовательно, равномерно сходятся и интегралы
∫
∫
∫
для всех таких, что
|
|
и всех таких, что
. Точно также
устанавливается равномерная сходимость интегралов
∫
∫
∫
Отсюда следует, что интеграл Пуассона:
√
∫
(
)
Можно дифференцировать по параметру, стоящему под знаком интеграла, и
для него справедливо равенство
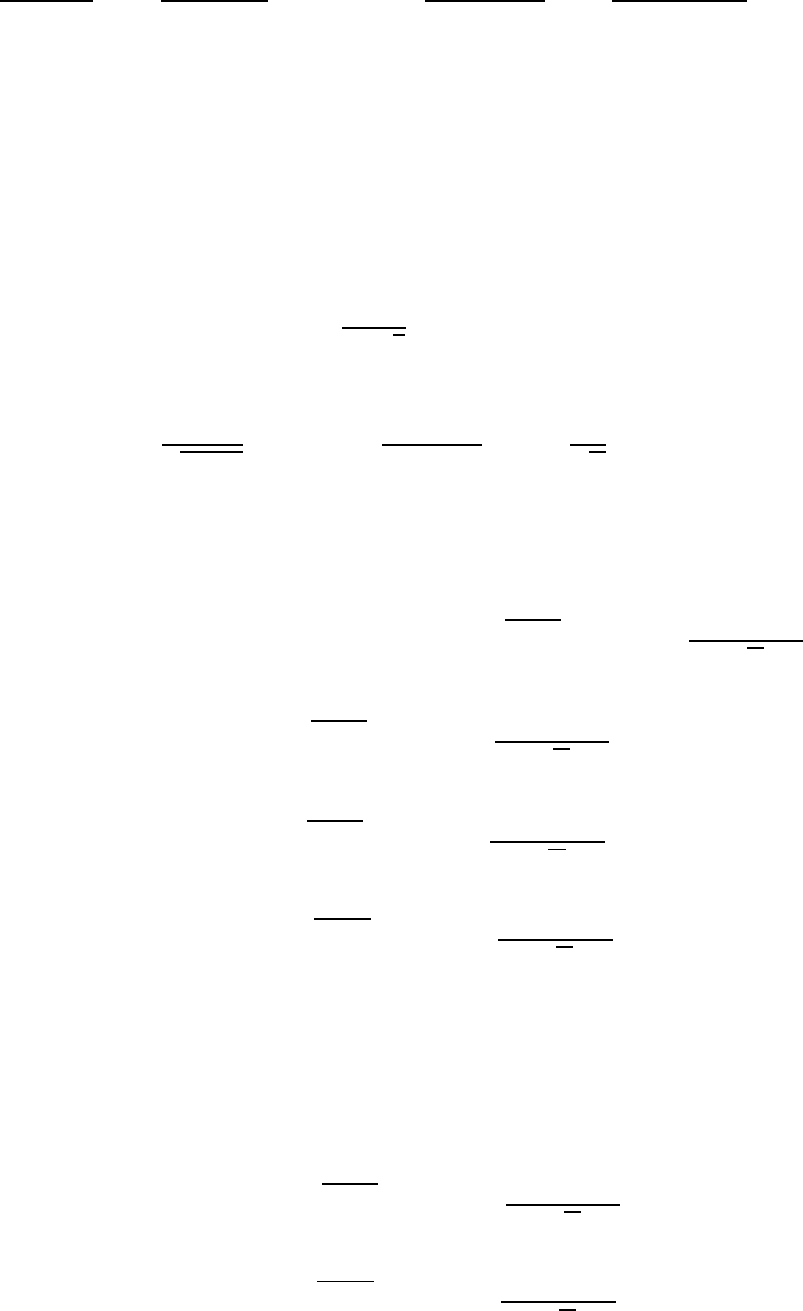
43
∫
(
)
Тем самым доказано, что интеграл Пуассона является решением уравнения
теплопроводности.
Покажем, что во всякой точке
непрерывности функции
имеет
место равенство
Для этого выберем и построим окрестность точки
такую, что
|
|
для всех точек
из этой окрестности. Полагая
√
получим
∫
√
∫
(
)
√
∫
|
|
|
∫
∫
|
∫
|
|
∫|
(
√
)
|
√
∫ |
(
√
)
|
√
∫|
(
√
)
|
√
∫|
(
√
)
|
√
Так как
|
|
для всех
и интеграл
∫
сходится, то можно выбрать столь большое N, чтобы каждый из интегралов
∫ |
(
√
)
|
√
∫|
(
√
)
|
√
был меньше . При выбранном N рассмотрим интеграл
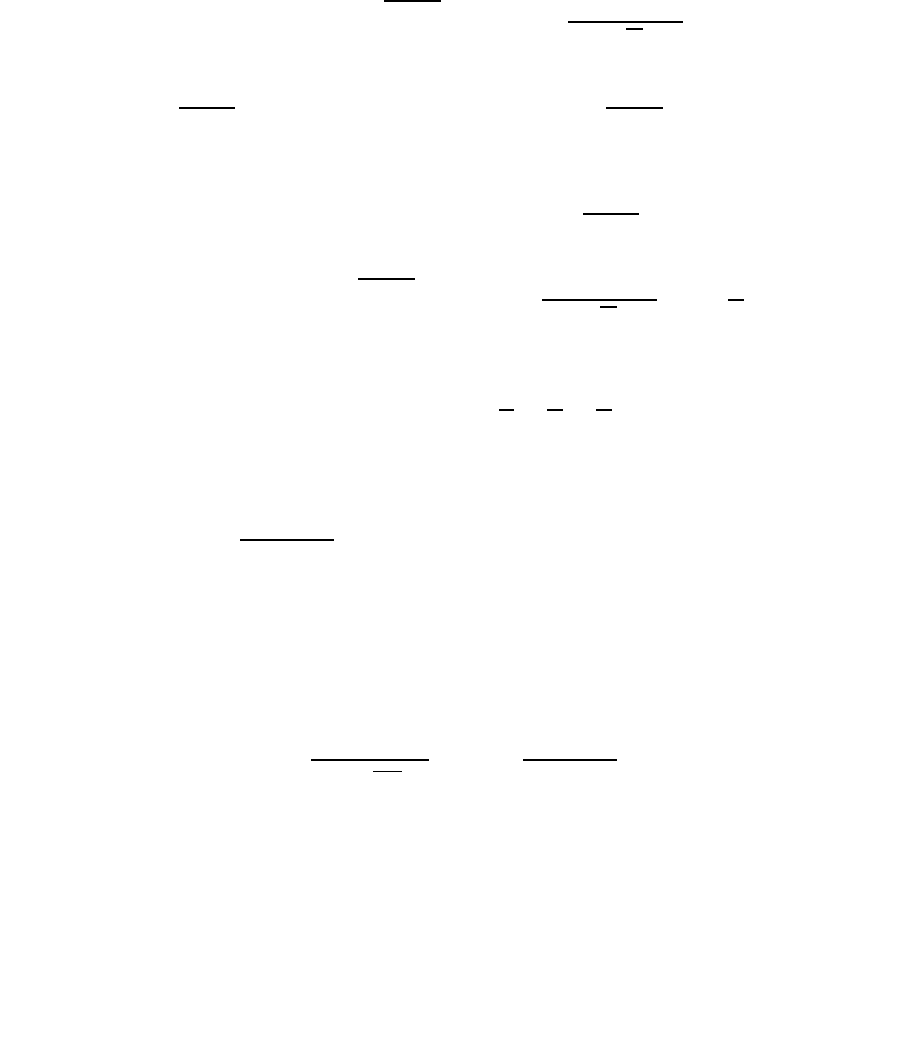
44
∫|
(
√
)
|
√
Так как функция
непрерывна в точке
, то существует
такое,
что
|
(
√
)
|
при
|
√
|
. Последнее
неравенство выполнится при всяком
, если выбрать такую
окрестность точки
, чтобы для всех точек
из этой окрестности
выполнялись неравенства
|
|
и √
. Тогда
∫|
(
√
)
|
√
Оценки всех трех интегралов позволяют утверждать, что
|
с
|
Все рассуждения, приведенные выше, справедливы для произвольного
. Так что решением задачи Коши
с начальным условием
, является интеграл Пуассона
∫
Здесь
{
(
√
)
(
|
|
)
при
при
|
|
∑
1.23 Постановка задач для уравнений Лапласа и Пуассона
Рассмотрим простейшие из эллиптических уравнений: уравнения
Лапласа и Пуассона. Будем использовать следующие обозначения: , –
точки -мерного пространства
. Например, пусть для
с нор-
мой
|
|
∑
задана функция . Тогда неоднородное уравнение

45
∑
называется уравнением Пуассона. Если , то уравнение Пуассона, в
частности, имеет вид уравнения
∑
называемого уравнением Лапласа. Часто пользуются более краткой формой
записи уравнения Лапласа:
и уравнения Пуассона:
,
где называют оператором Лапласа. Выберем – ограниченную область из -
мерного евклидового пространства
, имеющую границу , которую бу-
дем считать всюду кусочно-гладкой. Обозначим через
внешнюю нормаль к . Для уравнения Пуассона обычно формулируются
следующие три задачи.
Требуется найти дважды непрерывно дифференцируемую в области
функцию , удовлетворяющую в уравнению
и одному из
условий:
1) функция непрерывна в и на границе принимает за-
данное значение (первая краевая задача или задача Дирихле);
2) функция в каждой точке границы имеет предельное значение
нормальной производной
∑
совпадающее с заданной функцией
|
(вторая краевая задача или задача Неймана);
3) функция непрерывна в , в точках границы существует
предельное значение нормальной производной и
(
)|
где
– заданные непрерывные функции (третья краевая задача).
Если во всех перечисленных выше случаях решение ищут не внутри
ограниченной области , а вне этой области, то говорят о внешних краевых
задачах, в отличие от рассмотренных выше внутренних задач. При рассмот-
рении внешних задач на решение налагается так называемое условие регу-
лярности на бесконечности. В случае требуют, чтобы решение было
ограниченным при стремлении модуля аргумента к бесконечности. Если же
, то требуют, чтобы при
|
|
решение стремилось к нулю не мед-
леннее чем
|
|
. Функции, удовлетворяющие в некоторой области уравне-
нию Лапласа, называют гармоническими в этой области. Можно рассматри-
вать обобщения сформулированных выше задач, когда, например, на части
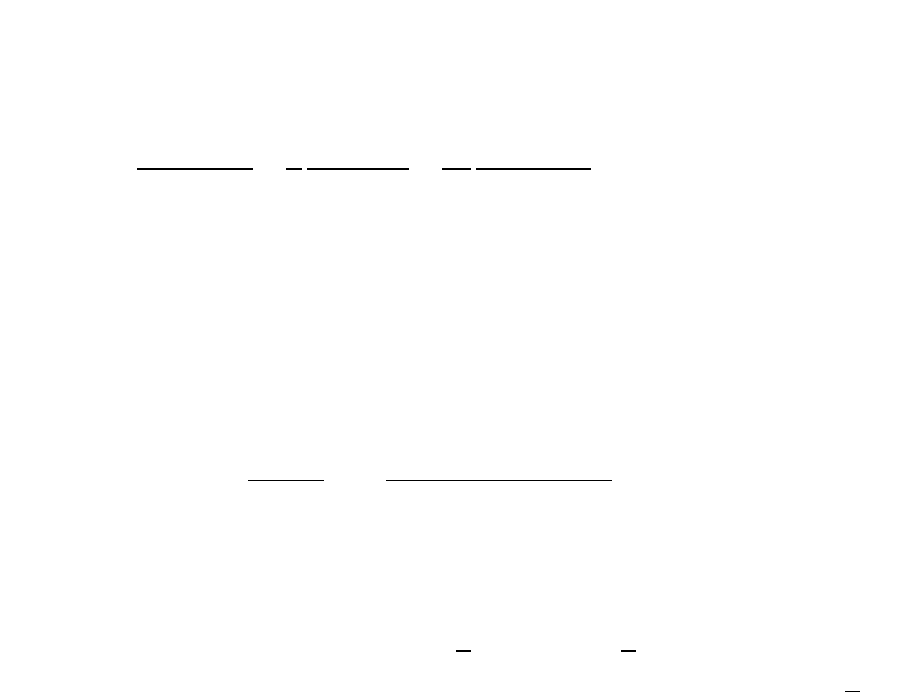
46
границы области задается условие Дирихле, на другой части – Неймана, на
третьей – третье краевое условие.
1.24 Решение задачи Дирихле для уравнения Лапласа в кольце и
круге методом Фурье
Рассмотрим задачу Дирихле для уравнения Лапласа в кольце:
|
|
Здесь и – полярные координаты,
и
– заданные функции от
, обладающие периодом, равным . Применим метод разделения перемен-
ных для решения этой задачи. Нетривиальное решение задачи Дирихле будем
искать в виде . Подставляя эту функцию в уравнение
Лапласа, и, разделяя переменные, получим
Для периодической функции
получаем уравнение .
Если , то решение этого уравнения запишется в виде линейной комби-
нации экспонент и не будет периодическим. При получается периоди-
ческая функция . При решение имеет вид
(
√
)
(
√
)
и будет периодическим с периодом только в том случае, когда
√
–
целое число. Итак,
,где .
Функция находится из решения линейного уравнения второго по-
рядка с переменными коэффициентами:
При его линейно независимые решения: и ; при :
и
.
Общее решение получается как линейная комбинация всех линейно незави-
симых решений. Таким образом, решение уравнения Лапласа в полярной си-
стеме координат можно представить в виде
∑
∑
{
}
где
– постоянные величины, определяемые из краевых условий.
При :
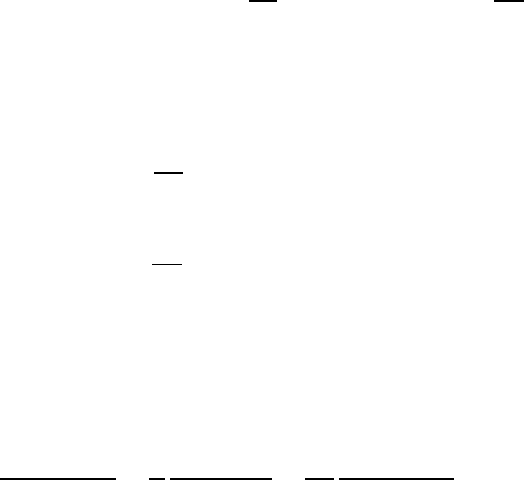
47
∑
{
}
При :
∑
{
}
Если ввести обозначения:
то последние соотношения для краевых условий перепишутся в виде:
∑(
)
∑(
)
Эти соотношения являются разложениями в ряды Фурье функций
,
, и, следовательно, позволяют найти коэффициенты
,
,
,
, а затем и коэффициенты
.
Рассмотрим задачу Дирихле для уравнения Лапласа в круге:
|
Здесь, как и ранее и – полярные координаты,
– заданная функция
от с периодом, равным . Как и для случая задачи в кольце, будем искать
нетривиальное решение уравнения Лапласа в виде . Раз-
деляя как и ранее переменные, получим те же значения для
,
и такое
же уравнение для
. Отличие этой задачи от задачи в кольце состоит в
том, что решение задачи в круге должно быть ограниченным. Поэтому сле-
дует взять только ограниченные решения для
, то есть отбросить реше-
ния и
. В результате получим
∑
∑
(
)
Для определения коэффициентов
и
воспользуемся граничным услови-
ем
∑
(
)
Если эту функцию
сравнить с ее представлением в виде ряда Фурье
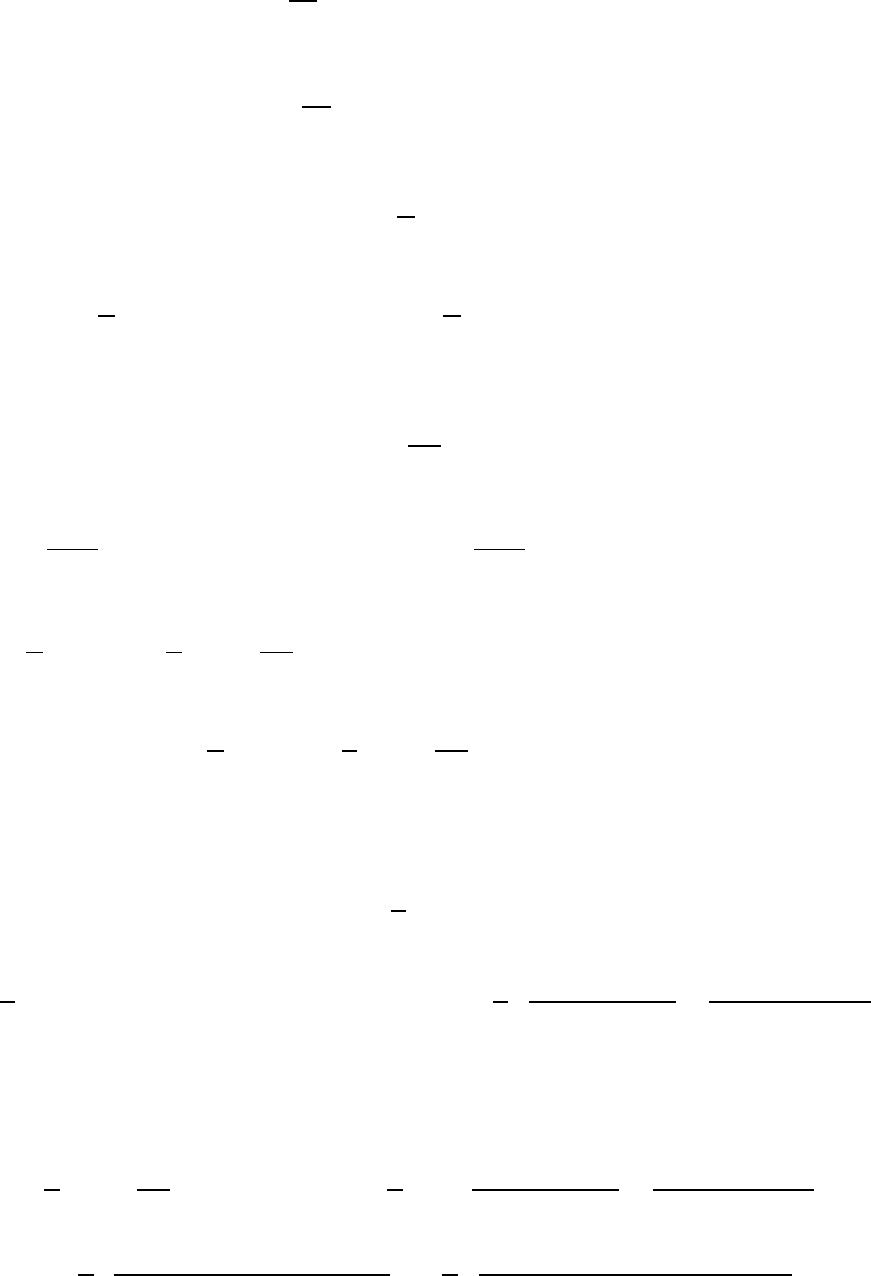
48
∑(
)
получим
причем коэффициенты ряда Фурье находятся по формулам
∫
∫
∫
Таким образом, получим
∫
∑.
∫
∫
/
∫
(
∑
(
)
)
∫
{
∑
}
Обозначим , и сумму, стоящую под знаком интеграла, преобразуем к
двум бесконечно убывающим геометрическим прогрессиям
∑
∑
(
)
(∑(
)
∑(
)
)
(
)
Затем выражение, стоящее в фигурных скобках под знаком интеграла, приве-
дем к общему знаменателю, вернемся к прежней переменной . Полу-
чим
{
∑
}
(
)
(
)
(
)
Окончательно решение задачи Дирихле для уравнения Лапласа внутри круга
можно представить в виде интеграла

49
∫
(
)
который называют интегралом Пуассона. Этот интеграл получен в предпо-
ложении . При он теряет смысл. Однако можно доказать, что ес-
ли непрерывная функция, то интеграл Пуассона удовлетворяет уравне-
нию Лапласа внутри круга и
Таким образом, функция
при
∫
(
)
при
удовлетворяет уравнению Лапласа внутри круга, непрерывна в объединении
круга и окружности, то есть является решением задачи Дирихле.
1.25 Метод Даламбера
Обширный класс физических задач связан с волновым уравнением.
Общее решение этого уравнения получено Даламбером. Рассмотрим метод,
предложенный Даламбером, на примере одномерного и однородного волно-
вого уравнения:
удовлетворяющего начальным условиям при :
Для этого преобразуем волновое уравнение к новым независимым перемен-
ным
или
Применяя правило дифференцирования сложной функции, вычислим первые
производные
(
)
затем вторые производные
(
)
Получим соотношение
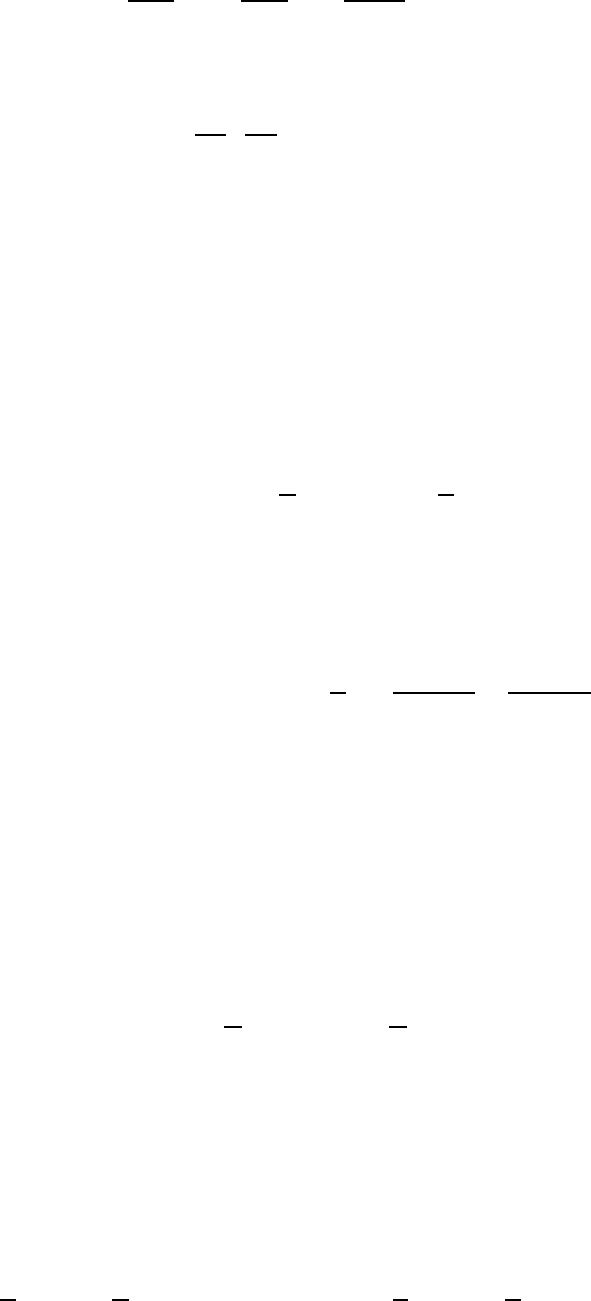
50
из которого следует, что исходное волновое уравнение равносильно уравне-
нию
(
)
решением которого является
∫
где
есть произвольная функция от («постоянная» при интеинтегриро-
вании по может зависеть от ). Первое слагаемое можно считать здесь про-
извольной функцией от , так как
есть произвольная функция . Обо-
значим ее через
. Получим
или, переходя к старым переменным ,
(
)
(
)
Здесь
и
– произвольные функции своих аргументов. Это самое общее
решение одномерного и однородного волнового уравнения называется ре-
шением Даламбера. Оно содержит две произвольные функции
и
. Для
их определения воспользуемся начальными условиями:
(
)
Из второго равенства следует
∫
Из него при получаем значение постоянной интегрирования
Не ограничивая общности, можем считать . Так как если бы оказалось
, то, введя вместо функций
,
функции
не меняя начальных условий, удовлетворили бы равенству
Итак, из начальных условий в виде
∫
можно определить
∫
∫
И окончательно
