Попов В.А. Математические методы моделирования физических процессов
Подождите немного. Документ загружается.


71
где постоянные
,
. Для ограниченных функций
. Число
называют показателем роста функции
. Итак, несобственный инте-
грал сходится при условии
|
|
если
Действительно, несобственный интеграл
∫
мажорируется сходящимся интегралом
∫
|
следовательно, и сам сходится. Окончательно получаем, что изображение
производной
можно выразить через изображение
искомой
функции
в форме:
Далее выразим изображение
производной
через изображение
искомой функции
. Для этого дважды применим метод интегриро-
вания по частям:
∫
(
)|
∫
При условии, что
растет не быстрее экспоненты
|
|
аналогично предыдущему получаем
И далее, методом дедукции можно установить, что для всех
В частности, при нулевых начальных данных
имеем
В общем же случае операторное уравнение примет вид
где
– многочлен степени, не выше, чем относительно
. Из операторного уравнения находим изображение решения задачи
Коши:

72
Теперь по известному изображению
найдем соответствую-
щий ему оригинал , являющийся решением задачи Коши. Иными слова-
ми, нужно решить задачу обращения преобразования
∫
Выбор функции
, которая пока что является произвольной аналити-
ческой функцией, и определяется условиями обращения этого преобразова-
ния. Представим это условие в виде
∫
напоминающем известное преобразование Фурье
∫
которое ставит в соответствие некоторой функции
другую функцию
. Обращение этого преобразования имеет вид
∫
Фурье-преобразование существует, если
на любом конечном интервале
непрерывна, или кусочно-непрерывна, и абсолютно интегрируема на
, то есть интеграл
∫
|
|
сходится. Для того, чтобы интересующее нас обращение выполнить с помо-
щью преобразования Фурье, необходимо в интеграле
∫
1. Заменить нижний предел на . Это возможно, если потре-
бовать
при .
2. Положить
, тем самым определяются
и
. Тогдапреобразование
∫
существует в правой полуплоскостипри
комплексной плоскости
.
3. Зафиксировать параметр , положив
.
При выполнении этих трех условий получим преобразование

73
∫
Имеющее вид преобразования Фурье для функции
. Тогда, в
соответствии с обратным преобразованием Фурье
∫
или
∫
Возвращаясь к первоначальной переменной и учитывая, что под
знаком интеграла
фиксировано, получаем
∫
Здесь интегрирование ведется в комплексной области вдоль любой верти-
кальной прямой, проходящей правее точки
.
3.2 Преобразование Лапласа
Преобразованием Лапласа называется преобразование,которое ставит
в соответствие функции
другую функцию
:
∫
а сам интеграл – интегралом Лапласа. Функцию
, определяемую этим
равенством, называют изображением по Лапласу оригинала
. Функ-
цию
называют оригиналом по Лапласу если эта функция непрерывна
или кусочно-непрерывна на любом конечном интервале, принадлежащем
, возрастает не быстрее экспоненты и
при .Формула
∫
дает обращение преобразования Лапласа во всех точках непрерывности ори-
гинала.
В дальнейшем будем обозначать оригиналы строчными буквами
,
и т. д., а соответствующие им изображения – теми же прописными бук-
вами
,
и т. д. Принята символическая запись
, означаю-
щая, что «оригинал
имеет изображение
», а также запись
, означающая, что «изображение
имеет оригинал
».
Простейшие свойства преобразования Лапласа:

74
1. Линейность. Если
и
– оригиналы, причем
и
, то
где
и
– произвольные постоянные.
2. Подобие. Если
– оригинал и
, то при любом положи-
тельном числе
(
)
3. Дифференцирование оригинала. Если
– оригинал (тогда
также оригинал) и
, то
или в более общем случае
4. Дифференцирование изображения. Если
– оригинал и если
, то
5. Интегрирование оригинала. Если
– непрерывный оригинали
, то
∫
6. Деление оригинала на аргумент. Если
– оригинал и если
, то
∫
где
∫
∫
7. Запаздывание оригинала. Если
– оригинал и
, то
где – любое положительное число. Оригинал
называется запазды-
вающим.
8. Умножение оригинала на показательную функцию. Если
–
оригинал и
, то
где – любое комплексное число.
9. Сверткаоригиналов соответствует произведению их изображений:
Пусть
и
– два непрерывных оригинала, причем
и
. Сверткой оригиналов
и
называют интеграл
75
∫
Отметим, что свертка оригиналов является оригиналом. Она обладает
свойством симметрии: . Дифференцирование свертки приводит
к формулам
∫
∫
известным как формулы Дюамеля.
3.3 Обращение преобразования Лапласа
Формула обращения преобразования Лапласа во всех точках непре-
рывности оригинала, часто называемая формулой Меллина, имеет вид
∫
Здесь
– произвольное фиксированное значение; несобственный интеграл
(интеграл Меллина) вычисляется вдоль прямой
и понимается в
смысле главного значения:
∫
∫
Используя методы теории функций комплексного переменного, полу-
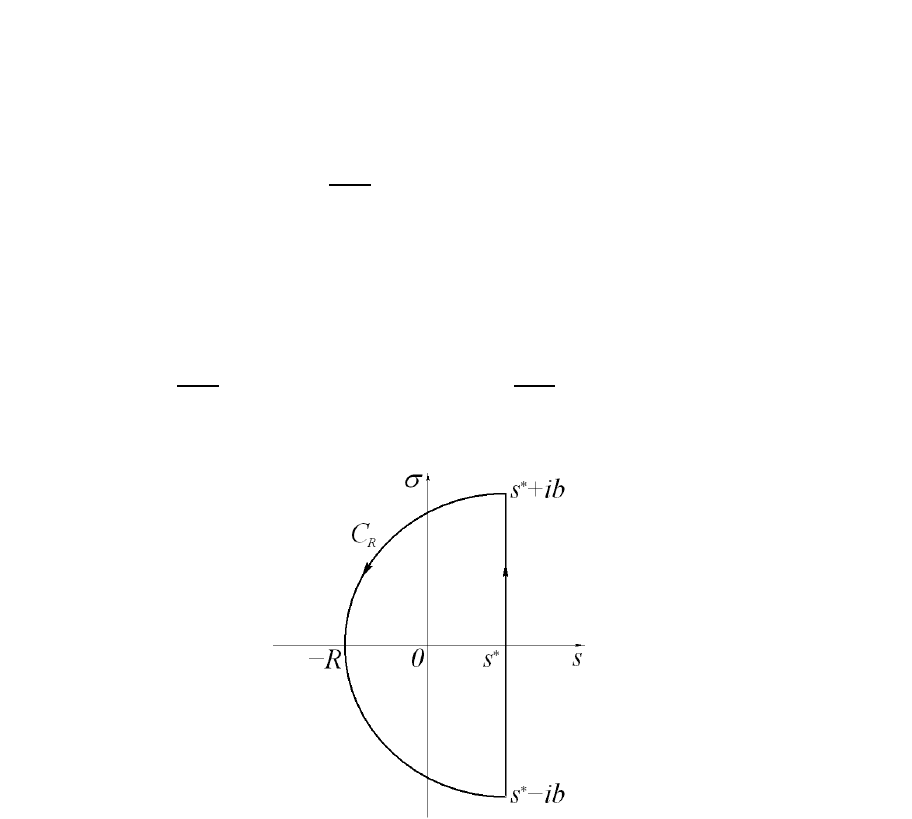
чим компактные формулы его представления. Для этого рассмотрим инте-
грал от
по замкнутому контуру
, состоящему из отрезка прямой

76
и дуги окружности
, проходящей через особые точки
изображения
. По основной теореме о вычетах имеем
∫
∫
∑
где
– особые точки изображения
, лежащие внутри контура интегри-
рования и пронумерованные в порядке неубывания их модуля. Будем дис-
кретно увеличивать радиус дуги
так, чтобы в каждом ее новом положе-
нии на ней не оказывалось особых точек изображения
. Тогда в пределе
при (при этом ) получаем
∫
∫
∑
Пусть изображение
аналитично в бесконечно удаленной точке и
|
|
то в соответствии с леммой Жордана
∫
Таким образом, формула обращения преобразования Лапласа может быть
представлена в виде
∑
где суммирование ведется по всем особым точкам изображения
. Она
определяет оригинал в виде разложения в ряд из вычетов произведения
Пусть изображение
, аналитичное в окрестности , задано в
виде лорановского разложения в этой окрестности:
∑
Умножим это равенство почленно на
, где – любое положительное чис-
ло; разделим на и проинтегрируем по замкнутому контуру
. Получим
∮
∑
∮
Преобразуем правую часть этого равенства.
∑
∮
∑

77
∑
∑
(
)
∑
Тогда
∮
∑
Записанное здесь соотношение выполняется при любых достаточно больших
|
|
. В пределе при получаем в левой части этого равенства инте-
грал, имеющий смысл
. Таким образом, оригиналом является ряд:
∑
Это разложение получено при любых положительных значениях , значит
сходится на всей комплексной плоскости и, следовательно, представляет со-
бой целую функцию. Из оценок для коэффициентов ряда Лорана
|
|
легко проверить справедливость соотношения
|
|
|
|
показывающего, что полученное представление для
в виде ряда, растет
не быстрее экспоненты, как и положено оригиналу.
3.4 Решение уравнения теплопроводностис использованием преоб-
разования Лапласа
Рассмотрим применение операционного с использованием преобразо-
ванием Лапласа для решения задачи о распространении тепла по полубеско-
нечному стержню.
Пусть требуется найти распределение температуры в полубесконечном
стержне , если начиная с момента времени на его левом
конце поддерживается заданный температурный режим. Начальная
температура стержня равна нулю. Математическая задача заключается в
определении ограниченного в области , решения
уравнения
с дополнительными условиями
где
– задан-
ная функция времени, удовлетворяющая по предположению условиям суще-
ствования преобразования Лапласа. Предположим, искомое решение ,
а также его производные, входящие в уравнение теплопроводности, удовле-
творяют условиям существования преобразования Лапласа по , причем
условия ограниченности степени роста по функции и ее производ-
ных не зависит от .
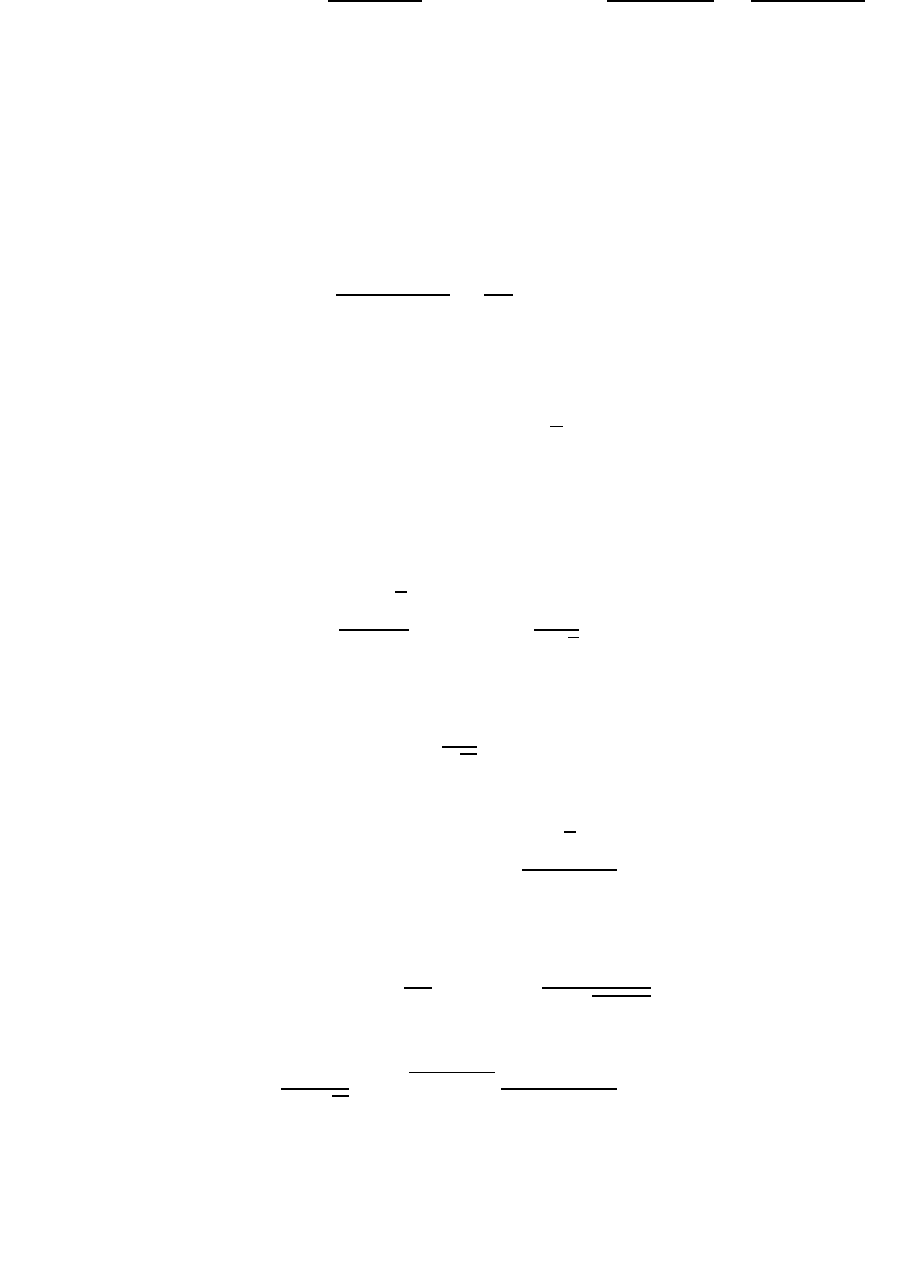
78
Вторая из этих формул получена с учетом начального условия
.
Третья формула имеет место в силу того, что сделанных предположений до-
статочно для вычисления производных несобственных интегралов, завися-
щих от параметра, путем дифференцирования по параметру подынтеграль-
ных функций.
Перейдя к изображениям, вместо исходной краевой задачи для функ-
ции получаем краевую задачу для изображения:
с дополнительными условиями
|
|
. Получена
краевая задача для обыкновенного дифференциального уравнения, в котором
переменная играет роль параметра. Решение этой задачи имеет вид
√
По этому изображению с помощью формулы Меллина может быть найдена
. Однако, в случае произвольной функции
вычисление соответ-
ствующего интеграла Меллина может привести к значительным трудностям,
обойти которые можно следующим образом. Заметим, что
√
(
√
)
где функция
√
∫
есть так называемая функция ошибок. Поэтому применяя к представлению
√
свойство свертки, получим
∫
(
(
√
))
√
∫
3.5 Решение краевой задачи для уравнения в частных производных
с использованием преобразования Лапласа
Метод, изложенный в предыдущем параграфе, может быть формально
перенесен и на решение краевой задачи для уравнения в частных производ-
ных более общего вида. Рассмотрим уравнение
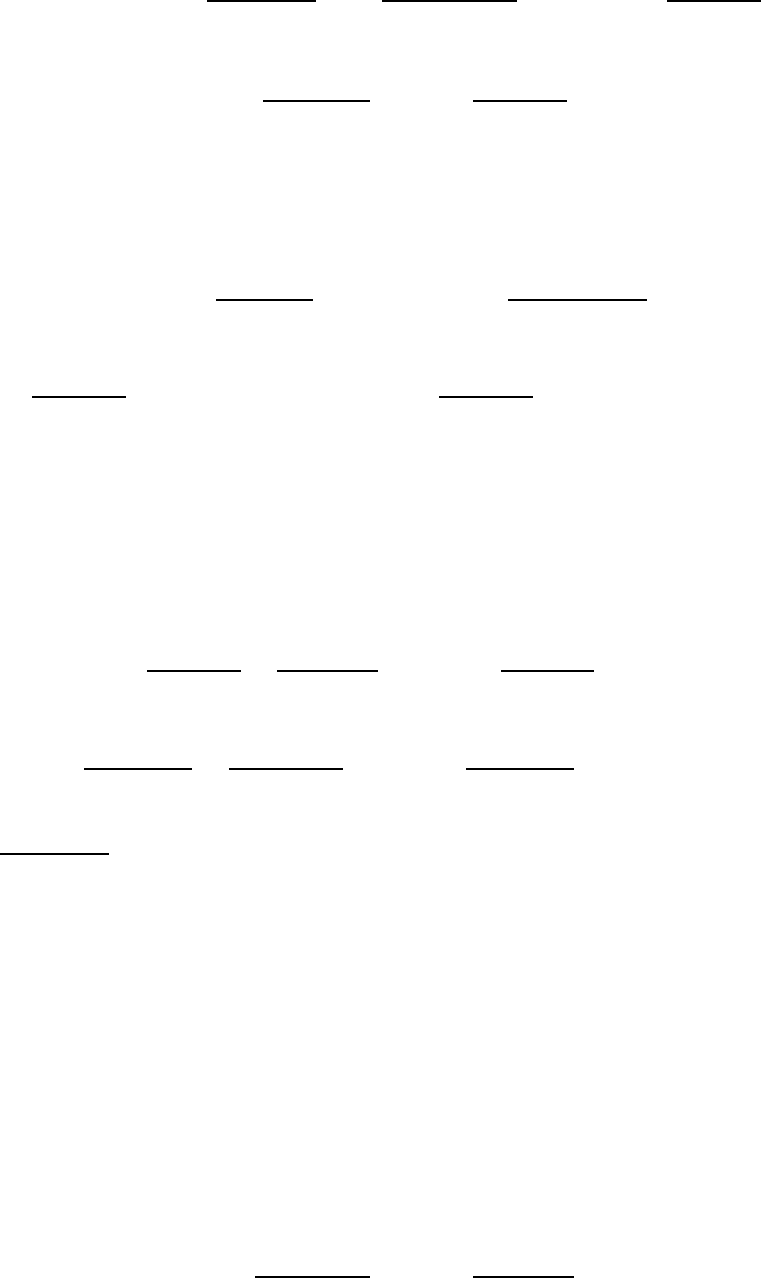
79
[
]
[
]
где
[
]
– линейный дифференциальный оператор с постоянными ко-
эффициентами, имеющий вид
[
]
[
]
– линейный дифференциальный оператор второго порядка вида
[
]
коэффициенты которого
являются функциями одной
независимой переменной .
– заданная функция переменных и до-
статочно гладких в области решения задачи. Будем искать решение
в
области , , удовлетворяющее начальным условиям
и граничным условиям
Будем предполагать, что существуют изображения Лапласа по функции
и всех ее производных, входящих в исходное дифференциальное
уравнение в частных производных:
∫
∫
∫
Кроме того, предположим, что существуют изображения по функций:
Тогда, переходя к изображениям в исходном дифференциальном уравнении
в частных производных, получим обыкновенное дифференциальное уравне-
ние второго порядка для функции
независимой переменной :
[
]
где
∑
[
]

80
Полученное обыкновенное дифференциальное уравнение второго порядка
для функции
независимой переменной и параметром надо решать
с граничными условиями:
Обратный переход от изображения
к решению исходной задачи
может быть произведен с помощью формулы Меллина:
∫
Однако, в случае произвольной функции
вычисление соответствую-
щего интеграла Меллина может привести к значительным трудностям, обой-
ти которые можно применяя свойства свертки, например, как это сделано в
конце предыдущего параграфа. Использование формул преобразования
Лапласа может существенно облегчить эту задачу. Таблица основныхформул
преобразования Лапласа приведена в приложении.
3.6 Преобразование Фурье
Пусть имеем функцию
, абсолютная величина
|
|
которой инте-
грируема на интервале , т.е.
∫
|
|
тогда функция
√
∫
(
или
√
∫
)
называется преобразованием Фурье функции
или спектральной функ-
цией. Соответствующее преобразование
√
∫
(
или
√
∫
)
называется обратным преобразованием Фурье. Используя эти два преобра-
зования, прямое и обратное, получим интегральную формулу Фурье:
∫
∫
Стоящий в ее правой части интеграл называют интегралом Фурье.
Важную роль в применении преобразования Фурье при решении урав-
нений играет теорема о свертке. Прежде чем формулировать эту теорему,
рассмотрим
и
– преобразования Фурье функций
и
соответственно. Тогда
