Попов В.А. Математические методы моделирования физических процессов
Подождите немного. Документ загружается.


51
(
(
)
(
))
∫
Эта формула дает дважды непрерывно дифференцируемое решение, так
называемое классическое решение задачи, если
имеет непрерывные
производные
и
, а
– непрерывную производную
при
. Однако нередко приходится иметь дело с задачами, в которых
начальное возмущение задается функциями, не удовлетворяющими этим
условиям. Например, если струна в начальный момент имеет форму ломаной
линии, то
не имеет определенной производной в вершине ломаной. Тем
не менее разумно считать, что полученная формула дает решение задачи, хо-
тя функция
и не всюду имеет непрерывные производные до второго
порядка. В этом случае говорят, что задача имеет так называемое обобщен-
ное решение.
1.26 Ортогональные системы функций
Система функций
называется ортогональ-
ной с весом
на отрезке
[
]
, если
∫
Если каждая функция из ортогональной системы такова, что
∫
|
|
то такая система функций называется ортонормированной. Пусть
–
произвольная функция, определенная на отрезке
[
]
. Рядом Фурье этой
функции по ортогональной системе
{
}
называется ряд
коэффициенты которого
∫
∫
|
|
называются коэффициентами Фурье функции
по ортогональной си-
стеме
{
}
. При исследовании рядов Фурье важную роль играет квадра-
тичное отклонение функции
от n-ой частичной суммы
ее ряда
Фурье, по определению равной
∑
Квадратичное отклонение двух функций
и
на отрезке
[
]
с ве-
сом
определяется равенством

52
.
∫
|
|
/
Сформулируем следующие утверждения:
1. С возрастанием числа квадратичное отклонение
уменьшает-
ся и при оно стремится к некоторому неотрицательному числу.
2. При фиксированном имеет место неравенство
, где
– какая угодно линейная комбинация из первых функций системы
{
}
:
∑
Иными словами, среди всех линейных комбинаций функций
наиболее близкой к
будет та, коэффициенты которой равны соответ-
ствующим коэффициентам Фурье. Если
при , то говорят,
что ряд Фурье сходится к
в среднем квадратичном. Для сходимости к
в среднем квадратичном необходимо и достаточно выполнение равен-
ства Парсеваля:
∑
∫
|
|
∫
|
|
Ортогональная система
{
}
называется замкнутой, если для всякой
функции
, определенной на отрезке
[
]
, ряд Фурье для этой функции
сходится к ней в среднем квадратичном. Иными словами, система
{
}
замкнута, если равенство Парсеваля имеет место для любой функции
из
семейства функций, определенных на отрезке
[
]
.
В качестве конкретных ортогональных систем могут быть выбраны:
системы синусов, косинусов, системы функций Бесселя, Лежандра, Лагерра,
полиномы Чебышева, Лежандра, Эрмита, Лагерра и др.
Применим метод Фурье для решения неоднородного уравнения в част-
ных производных второго порядка
где
– заданная непрерывная функция, отличная от нуля, как в случае
однородного уравнения; – постоянные величины. Будем считать,
что на искомую функцию
наложены дополнительные (однородные и
неоднородные) граничные и начальные условия. Решение этого уравнения
представим в виде ряда Фурье
∑
по некоторому набору ортогональных функций
{
}
, удовлетворяющих
граничным условиям исходной задачи. Разложим
в ряд Фурье по тому
же набору функций
53
∑
Подставим эти разложения в исходное уравнение. Получим
∑(
)
∑(
)
Будем считать решенной задачу Штурма-Лиувилля о нахождении собствен-
ных значений
и собственных функций
дифференциального уравне-
ния
с граничными условиями исходной задачи. Тогда из полученного соотноше-
ния
∑
∑(
)
следует, что коэффициенты при
в левой части и в правой части этого
равенства должны равняться друг другу
Из полученной системы обыкновенных дифференциальных уравнений мож-
но найти все
, удовлетворяющие начальным условиям.

54
2 Теория специальных функций
2.1 Мультипликативное разделение переменных
Мультипликативная форма представления функции – это представ-
ление функции нескольких переменных в виде произведения функций. Ме-
тод разделения переменных, или метод Фурье – это метод, в котором реше-
ние дифференциальных уравнений в частных производных с заданными
начальными однородными и краевыми условиями ищется как суперпозиция
решений, удовлетворяющих краевым условиям и представимых в виде про-
изведения функций. Применение метода Фурье для решения линейных задач
математической физики приводит к обыкновенным дифференциальным
уравнениям, решения которых не выражаются через известные элементарные
функции. Такие решения называются специальными функциями. В частно-
сти, к обыкновенным дифференциальным уравнениям такого типа приводит
решение методом Фурье задач для уравнения Лапласа, теплопроводности,
диффузии, волнового уравнения. Найдем частные решения трехмерного
уравнения Лапласа .
В цилиндрических координатах (связанных с декартовыми ко-
ординатами соотношениями ) решение урав-
нения Лапласа
(
)
будем искать в виде произведения трех функций
. Подставим
это представление
в уравнение Лапласа, затем разделим
обе части равенства
на . Заметим, что полученное в результате этих преобразований выраже-
ние допускает разделение переменных.
Отсюда имеем два уравнения. Первое из них представим в виде:
где
– некоторая постоянная. Второе уравнение после умножения на
также допускает разделение переменных.
Отсюда опять имеем два уравнения. Одно из них представим в виде:
где
– некоторая постоянная. В другом:
сделаем замену переменной на . Получим уравнение цилиндриче-
ских функций
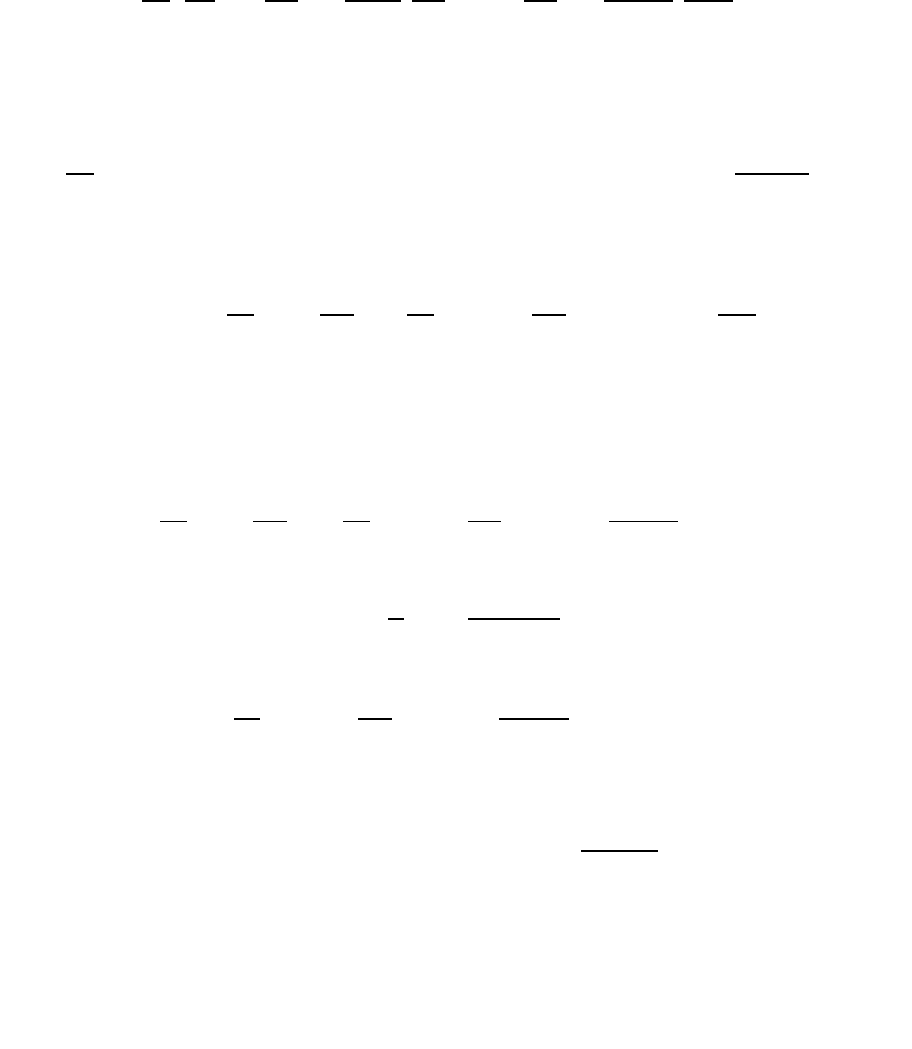
55
называемое также уравнением Бесселя. Любые решения этого
уравнения называют цилиндрическими функциями или функциями Бес-
селя.
Частные решения уравнения Лапласа в сферических координатах
(связанных с декартовыми координатами соотношениями
)
*
(
)
(
)
+
будем искать в виде произведения трех функций
. Под-
ставим это представление
в уравнение Лапласа, за-
тем обе части равенства
*
+
разделим на и умножим на
. Заметим, что полученное в резуль-
тате этих преобразований выражение допускает разделение переменных.
(
)
Отсюда имеем два уравнения. Первое из них представим в виде:
где
– некоторая постоянная. Второе уравнение после деления на
также допускает разделение переменных.
Отсюда опять имеем два уравнения. Одно из них представим в виде:
где
– некоторая постоянная. В другом равенстве
сделаем замену переменной на и преобразуем его к так называе-
мому уравнению Лежандра:
(
)
Любые решения этого уравнения называют присоединенными
функциями Лежандра степени и порядка .
2.2 Цилиндрические функции
Решения уравнения цилиндрических функций (уравнения Бесселя)

56
при произвольном значении параметра не выражаются через известные
элементарные функции. Поэтому будем искать решения этого уравнения в
виде степенного ряда
∑
Для определения постоянных величин и коэффициентов
подставим этот
ряд в уравнение Бесселя. После несложных преобразований получим
∑
∑
Это соотношение является справедливым при условии равенства нулю коэф-
фициентов при одинаковых степенях , то есть
при
при
при
при
при
Покажем, что
. Действительно, если
,
,
то полагая
,
для всех исходный ряд мож-
но привести к прежнему виду
∑
в котором
, что и требовалось показать. Таким образом, при
первое из уравнений полученной системы будет удовлетворено при
, то есть если . В этом случае
при
. Следовательно, из второго уравнения полученной системы имеем
, из четвертого:
, и так далее все коэффициенты с нечетными
номерами равны нулю, то есть
Для коэффициентов с четными номерами получаем
Отсюда
при
при
при
и, используя метод редукции, получаем, что

57
Так как уравнение Бесселя является однородным, решение определено с точ-
ностью до постоянного множителя. Положим
воспользуемся свойством гамма-функции
тогда
Таким образом, исходный ряд, содержащий коэффициенты с четными номе-
рами
∑
можно представить в виде
∑
(
)
Исследуем этот ряд на сходимость. По признаку Даламбера ряд
∑
сходится, если
|
|
Для нашего ряда с общим членом
(
)
при каждом фиксированном значении имеем
|
|
(
)
(
)
Таким образом, при любых и получаем два частных решения
уравнения Бесселя следующего вида:
∑
(
)
∑
(
)
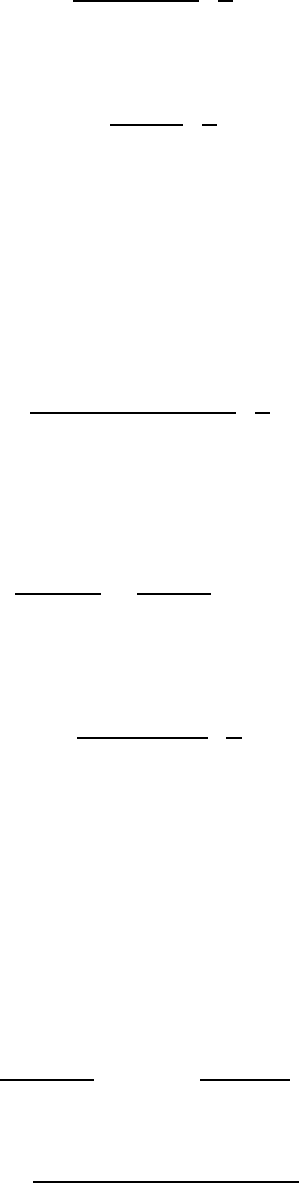
58
Функции
и
называют цилиндрическими функциями первого
рода (функциями Бесселя первого рода) порядка .
При , где – натуральное число, получаем
∑
(
)
и, в частности,
∑
(
)
При нецелых значениях ряды начинаются с различных степеней
и
. Функции
и
при таких значениях линейно независимы. По-
этому общее решение уравнения Бесселя при нецелых значениях можно за-
писать в виде линейной комбинации с произвольными постоянными
и
:
При , где – натуральное, получаем ряд
∑
(
)
содержащий первые слагаемых, равных нулю при за
счет того, что функция
обращается в нуль, а первый коэф-
фициент, отличный от нуля имеет вид:
Поэтому, вводя новый индекс суммирования , последний ряд мож-
но представить в виде:
∑
(
)
Эта функция Бесселя может отличаться от функции Бесселя с целыми поло-
жительными значениями индексов только знаком:
Таким образом, линейная зависимость
и
не позволяет записать
общее решение уравнения Бесселя в виде линейной комбинации этих функ-
ций. Для получения общего решения уравнения Бесселя, найдем функции,
линейно независимые с функцией
. Для этого достаточно выбрать в ка-
честве произвольных постоянных
Тогда получим частное решение уравнения Бесселя

59
линейно независимое с
. Поэтому при нецелых значениях общее ре-
шение уравнения Бесселя можно представить в виде линейной комбинации с
произвольными постоянными
и
:
Покажем, что при , где – натуральное число, функция
суще-
ствует. Для вычисления предела при воспользуемся правилом Лопита-
ля.
(
)
(
)|
(
)
∑
(
)
∑
(
)
(
)
В частности, при имеем
(
)
∑
(
)
Отметим, что
неограничена в нуле:
при
в отличие от функции
:
при
Функцию
называют цилиндрической функцией второго рода
(функцией Бесселя второго рода), или функцией Неймана порядка .
При решении ряда практических задач, связанных, в частности, с коле-
бательными процессами, часто используют другие частные решения уравне-
ния Бесселя:
Функции
и
, принимающие комплексно-сопряженные зна-
чения в одной и той же точке, называют цилиндрическими функциями
третьего рода (функциями Бесселя третьего рода), или функциями Хан-
келя первого и второго рода порядка .
2.3 Модифицированные функции Бесселя
В приложениях наряду с уравнением Бесселя

60
встречается модифицированное уравнение Бесселя (модифицированное
уравнение цилиндрических функций):
Будем искать решение этого уравнения с помощью такого же ряда
∑
который использовался при получении решения уравнения Бесселя. Для
определения постоянных величин и коэффициентов
подставим этот ряд
в модифицированное уравнение Бесселя. После несложных преобразований,
повторяя выкладки, приведенные в предыдущем параграфе, получим выра-
жение для ненулевых коэффициентов с четными номерами:
отличающееся от ранее полученных только знаком. Отсутствие знака
приводит к тому, что в выражениях для модифицированных функций Бесселя
∑
(
)
∑
(
)
под знаком суммы не будет множителя
. При нецелых эти ряды
начинаются с различных степеней и, следовательно, функции
,
линейно независимы. Поэтому общее решение можно записать в виде линей-
ной комбинации с произвольными постоянными
и
:
При , где – натуральное число, функции совпадают
,
поэтому не могут представлять общее решение. Для построения общего ре-
шения в линейной комбинации
положим
Тогда получим частное решение модифицированного уравнения Бесселя
линейно независимое с
, следовательно, для построения общего реше-
ния возможно представление в виде линейной комбинации с произвольными
постоянными
и
:
При , где – натуральное число, функция
также существует.
Для вычисления предела при воспользуемся правилом Лопиталя.
(
)
