Полшков Ю.Н. Курс лекций по экономико-математическому моделированию
Подождите немного. Документ загружается.

190
3. Вопрос о том, какую плату страховая компания должна назначать за то, что
принимает на себя тот или иной риск, крайне сложен. При его решении учиты-
вается большое число разнородных факторов: вероятность предъявления иска,
его ожидаемая величина и возможные колебания, связь с другими рисками, ко-
торые уже приняты компанией, организационные расходы компании на ведение
дела, соотношение между спросом и предложением по данному виду рисков на
рынке страховых услуг и т.д. Основным обычно является принцип эквивалент-
ности финансовых обязательств страховой компании и застрахованного. Одна-
ко нельзя выразить принцип эквивалентности обязательств равенством
p
X
=
,
поскольку
p
– детерминированная величина, а
X
– случайная.
Для решения этой проблемы рассмотрим следующую модель. Обычно
число застрахованных в страховой компании очень велико. Поэтому при нали-
чии большого числа однородных договоров в портфеле компании рассмат-
ривают коллективный или суммарный иск
N
12
...
NN
SXX X
=
+++,
где случайные величины
i
X
, – это индивидуальные иски, имеющие
одинаковые законы распределения.
1, 2,...,i= N
Такой подход позволяет применить гауссовскую модель, основанную на
центральной предельной теореме теории вероятностей. В простейшей форму-
лировке она выглядит так. Имеется достаточно большое число (хотя бы не-
сколько десятков) исков
i
X
, – независимых и одинаково распреде-
ленных. Т.о., у всех исков одинаковое математическое ожидание и одинако-
вое СКО
1, 2,...,i= N
X
m
X
σ
. Следовательно,
NX
M
SNm
=
⋅ ,
NX
DS N DX N
σ
=
⋅=⋅.
Рассмотрим центрированную и нормированную сумму величин исков
NNN
NX
SMS SNm
DS N
σ
X
−
−⋅
=
⋅
.
Согласно центральной предельной теореме, для любых действительных чисел
имеет место приближенное равенство
z
2
/2
11
()
2
2
z
t
NN
N
SMS
P
zedt
DS
π
−
−∞
⎛⎞
−
<≈ =+Φ
⎜⎟
⎜⎟
⎝⎠
∫
z
,
где – интегральная функция Лапласа, для которой имеются подробные
таблицы.
)(zΦ
Пусть число – это сумма от продажи полисов, собранная страховой
компанией. Может оказаться, что
z
N
Sz> ,
т.е. суммарный иск превысит денежные резервы компании. Тогда вероятность
()
N
PS z>
можно назвать вероятностью разорения страховой компании. Обозначим ве-
роятность разорения через
α
. Тогда имеем
191
1
()1()1
2
NN N N
NN
NN
SMS zMS zMS
PS z PS z P
DS DS DS
α
⎛⎞⎛
−− −
=>=−≤=− ≤ ≈−Φ
⎜⎟⎜
⎜⎟⎜
⎝⎠⎝
N
⎞
⎟
⎟
⎠
.
Число
N
N
z
MS
z
D
S
α
−
=
,
соответствующее вероятности разорения
α
называют квантилем уровня веро-
ятности
α
. Полезно иметь табл. 2 квантилей, отвечающих достаточно малой
вероятностью разорения
α
.
Табл. 2. Квантили
z
α
уровня вероятности
α
α
1% 2% 3% 4% 5%
z
α
2,33 2,05 1,88 1,75 1,645
Напомним, что согласно (5), страховая премия
p
слагается из нетто-
премии и страховой надбавки . Рассмотренная гауссовская модель позво-
ляем нам следующее. Для того, чтобы обеспечить малую вероятность разоре-
ния
X
m
X
l
α
страховой компании, страховая надбавка должна рассчитываться по
формуле
X
X
z
l
N
α
σ
⋅
= .
(6)
Заметим, что в этой страховой надбавке не учтены административные расходы
компании, ее прибыль и т.п. Число
X
X
X
X
z
l
m
mN
α
σ
θ
⋅
==
(7)
называют относительной страховой надбавкой. Ее часто выражают в процент-
ной форме.
Пример 2. Страховая компания заключила 10000 договоров страхования
жизни на условиях примера 1. Подсчитать величину страховой премии, обеспе-
чивающую малую вероятность разорения 5%. Определить относительную стра-
ховую надбавку.
Решение. Данные нашей задачи:
10000N
=
, 5%
α
=
, ,
5%
1, 645z = 1, 5 2
X
m
=
грн.,
31,74
X
σ
= грн. Страховая надбавка (6) равна
31,74 1,645
0,52
10000
X
l
⋅
== (грн.),
поэтому размер страховой премии (5) составляет
1,52 0,52 2,04p =+ = (грн.).
Относительная страховая надбавка (7) равна
0,52
34%
1, 52
θ
==.

192
4. Пусть портфель страховой компании состоит из групп однородных дого-
воров. Т.е. индивидуальные иски в каждой группе имеют одинаковые законы
распределения. Присвоим этим группам номера ,
k
i 1,2,...,ik
=
. Пусть в каждой
группе имеется договоров. Тогда весь портфель состоит из договоров, т.е.
i
N N
1
k
i
i
NN
=
=
∑
.
Обозначим через
i
X
случайную величину, означающую размер индиви-
дуального иска в
i -й группе. Введем случайную величину
1
k
Si
i
i
X
NX
=
=
∑
,
которую назовем суммарным иском. Для каждой группы рассчитаем основные
числовые характеристики: нетто-премию , дисперсию индивидуального иска
, СКО
i
m
i
D
i
σ
, коэффициент вариации . Тогда число – средняя величина сум-
марного иска или суммарная нетто-премия:
i
c
S
m
1
k
Si
i
mN
=
=
∑
i
m
i
D
i
.
(8)
Введем также суммарную дисперсию, суммарное СКО, суммарный коэффици-
ент вариации:
1
k
Si
i
DN
=
=
∑
,
1
k
Si
i
N
σ
σ
=
=
∑
,
1
k
Si
i
cN
=
=
∑
i
c.
(9)
Средства, собираемые страховой компанией от продажи полисов, назы-
вают резервами страховой компании . Резервы компании формируются сле-
дующим образом:
U
SS
Um l
=
+ ,
(10)
где – суммарная страховая надбавка. Согласно гауссовской модели:
S
l
SS
lDz
α
=
⋅ .
(11)
После определения суммарной надбавки , обеспечивающей малую вероят-
ность разорения
S
l
α
, нужно решить, как справедливым образом разделить ее ме-
жду всеми группами договоров. Имеются три принципа деления страховой
надбавки, а, значит, и назначения страховых премий: 1) пропорционально нет-
то-премиям, 2) пропорционально дисперсиям, 3) пропорционально СКО.
k
1) Если надбавка делится пропорционально нетто-премиям, то относи-
тельная страховая надбавка
S
l
θ
одинаковая для всех договоров и равна
S
S
l
m
θ
= .
(12)
Поэтому индивидуальные премии
i
p
, 1, 2,...,ik
=
равны
(1 )
ii
pm
θ
=
+ .
(13)

193
2) Если суммарной надбавка делится пропорционально дисперсиям, то
индивидуальные страховые надбавки рассчитываются по формуле:
S
l
i
l
S
ii
S
l
lD
D
=
⋅ ,
(14)
где число
S
S
l
D
играет роль коэффициента пропорциональности. Страховые пре-
мии вычисляются, как
iii
p
ml
=
+ ,
(15)
а относительные страховые надбавки
i
i
i
l
m
θ
= .
(16)
3) Если суммарной страховая надбавка делится пропорционально сред-
ним квадратическим отклонениям, то страховые надбавки рассчитываются
по формуле:
S
l
i
l
S
ii
S
l
l
σ
σ
=
⋅ ,
(17)
где число
S
S
l
σ
играет роль коэффициента пропорциональности. Страховые пре-
мии и относительные страховые надбавки вычисляются по формулам (15) и
(16), соответственно.
Заметим, что принцип 1) назначения премий не учитывает риска, связан-
ного с каждой группой договоров, и является, фактически, «уравниловкой».
Принципы же 2) и 3) лишены этого недостатка, т.к. обычно показателями риска
являются дисперсия или СКО.
В каждом конкретном случае следует выбирать: какой из принципов 1),
2) или 3) наиболее справедлив. Критерием выбора является средний коэффици-
ент вариации, рассчитанный по всему портфелю договоров:
S
c
c
N
=
,
(18)
где взят из (9). Коэффициент
S
c c разделит портфель договоров на две части
A
и
B
. В часть войдут те группы договоров, у которых A
i
cc
≤
,
а в часть
B
те, у которых
i
cc> .
Считается, что
c является показателем риска портфеля страховой компании.
Следовательно, часть вносит в портфель меньший риск, чем часть
A
B
. Поэто-
му группы договоров, вошедшие в
A
, должны нести меньшую финансовую на-
грузку. Т.о., следует выбрать тот принцип назначения страховых премий, кото-
рый бы уменьшал относительные страховые надбавки
i
θ
для групп договоров,
попавших в
A
, и увеличивал бы их для договоров из
B
.
Пример 3. Страховая компания заключила 10000 договоров страхования
жизни сроком на один год на следующих условиях: в случае смерти застрахо-
ванного в течении года от несчастного случая компания выплачивает наследни-

194
кам 1000 грн., в случае смерти от естественных причин 250 грн. и не платит ни-
чего, если застрахованный не умрет. Вероятность смерти от несчастного случая
для всех застрахованных 0,0005. Среди застрахованных две возрастные группы:
4000 человек в возрасте 28 лет и 6000 человек в возрасте 31 год.
Подсчитать величину резервов, обеспечивающую малую вероятность ра-
зорения компании, равную 5%. Обосновать распределение размеров страховых
премий среди возрастных групп.
Решение. Данные нашей задачи: общее число договоров ; число
возрастных групп
10000N =
2k
=
; численность групп
1
4000N
=
и ; вероятность
разорения компании
2
6000N =
5%
α
= ; квантиль
5%
1, 645z
=
;
28
0,0018q
=
и ; ве-
роятность смерти от несчастного случая ; страховые возмеще-
ния грн. и грн;
31
0,00207q =
(2) (2)
12
0,0005qq==
(1) (1)
12
250bb==
(2) (2)
12
1000bb==
(1) ( 2)
1281
0,0018 0,0005 0,0013qqq=− = − = ;
(0)
128
1 0,9982pq=− =
;
(1) ( 2)
2312
0,00207 0,0005 0,00157qqq=− = − = ;
(0)
231
1 0,99793pq=− =
.
Для 1-й группы договоров закон распределения индивидуального иска
1
X
име-
ет вид
i
x
0 250 1000
i
p
0,9982
0,0013
0,0005
Для 2-й группы договоров закон распределения индивидуального иска
2
X
име-
ет вид
i
x
0 250 1000
i
p
0,99793
0,00157
0,0005
По формулам (4.1)-(4.4) найдем основные числовые характеристики индивиду-
альных исков:
1
0,825m = (грн.), ,
1
580,5694D =
1
24,09501
σ
=
(грн.),
1
29,20607c
=
;
2
0,8925m = (грн.), ,
2
597,3284D =
2
24,4403
σ
=
(грн.), .
2
27,38409c =
Используя (8)-(9), получим числовые характеристики суммарного иска
S
X
:
4000 0,825 6000 0,8925 8655
S
m =⋅ +⋅ = (грн.),
4000 580,5694 6000 597,3284 5906248
S
D =⋅ +⋅ = ,
4000 24,09501 6000 24,4403 243021,9
S
σ
=
⋅+⋅= (грн.),
4000 29,20607 6000 27,38409 281128,8
S
c =⋅ +⋅ = .
По формуле (11) рассчитаем суммарную страховую надбавку
5906248 1,645 3997,81
S
l =⋅= (грн.).
Резервы компании вычислим по (9):
8655 3997,81 12652,81U =+ =
(грн.).
Рассмотрим три принципа назначения индивидуальных страховых пре-
мий: 1) пропорционально нетто-премиям, 2) пропорционально дисперсиям, 3)
пропорционально СКО.

195
1) Если надбавка делится пропорционально нетто-премиям, то относи-
тельная страховая надбавка
S
l
θ
одинаковая для всех договоров и рассчитывается
по (12):
3997,81
0,461907
8655
θ
== .
Поэтому (13) индивидуальные премии равны:
1
0,825 (1 0,461907) 1,206073p =⋅+ = (грн.),
2
0,8925 (1 0,461907) 1,304752p =⋅+ = (грн.).
2) Если суммарная надбавка делится пропорционально дисперсиям, то
индивидуальные страховые надбавки рассчитываются по формуле (14):
S
l
i
l
1
3997,81
580,5694 0,392974
5906248
l =⋅=
(грн.),
2
3997,81
597,3284 0,404318
5906248
l =⋅= (грн.).
Страховые премии вычислим согласно (15):
1
0,825 0,392974 1,217974p =+ = (грн.),
2
0,8925 0,404318 1,296818p =+ = (грн.).
Используя (16), получим относительные страховые надбавки
1
0,392974
0,476333
0,825
θ
==,
2
0,404318
0,453018
0,8925
θ
==.
3) Если суммарную страховую надбавку делить пропорционально
средним квадратическим отклонениям, то страховые надбавки вычисляются
по формуле (17):
S
l
i
l
1
3997,81
24,09501 0,396372
243021,9
l =⋅ = (грн.),
2
3997,81
24,4403 0,402053
243021,9
l =⋅ = (грн.).
Рассчитаем, согласно (15), страховые премии
1
0,825 0,396372 1,221372p =+ = (грн.),
2
0,8925 0,402053 1, 294553p =+ = (грн.).
По (16) найдем относительные страховые надбавки
1
0,396372
0,480451
0,825
θ
==,
2
0,402053
0,450479
0,8925
θ
==.
Теперь определим: какой из принципов назначения страховых премий 1),
2) или 3) наиболее справедлив. Для этого по (18) рассчитаем средний коэффи-
циент вариации портфеля договоров
281128,8
28,11288
10000
c ==.

196
Коэффициент c разделил портфель договоров на две части
A
и
B
. В часть
A
вошли те группы договоров, у которых
i
cc
≤
,
а в часть
B
те, у которых
i
cc> .
Итак,
A
включает в себя 2-ю группу договоров, а
B
– 1-ю группу. Т.к. c явля-
ется показателем риска портфеля страховой компании, то 2-я группа вносит в
портфель меньший риск, чем 1-я группа договоров. Поэтому 2-я группа должна
нести меньшую финансовую нагрузку. Следовательно, выберем тот принцип
назначения страховых премий, который уменьшает относительную страховую
надбавку
2
θ
и увеличивает
1
θ
.
Результаты по страховым надбавкам приведем в табл. 3.
Табл. 3. Индивидуальные страховые надбавки примера 3
Принцип 1) Принцип 2) Принцип 3)
1
θ
0,4619071 0,4763325 0,4804515
2
θ
0,4619071 0,4530176 0,4504793
Ответ: следует принять принцип 3), по которому суммарная страховая
надбавка делится пропорционально средним квадратическим отклонениям, в
качестве основы для назначения индивидуальных страховых премий.
197
Лекция 10. РИСКИ ПРИ ДОЛГОСРОЧНОМ СТРАХОВАНИИ ЖИЗНИ
План
1. Полное страхование жизни.
2. Модель де Муавра продолжительности жизни.
3. Страхование жизни на
n
лет.
4. Страхование жизни, отсроченное на
k лет.
5. Расчет индивидуальных премий при долгосрочном страховании жизни.
1. Ранее отмечалось, что при краткосрочном страховании жизни договора стра-
хования заключались на относительно короткий период, не учитывался доход,
который со временем приносят деньги и фактор инфляции.
В случае долгосрочного страхования жизни сумма в грн. спустя лет
превратится в сумму
S T
T
Se
δ
⋅
, где
δ
– непрерывная процентная ставка. Напомним,
что в лекции 2 было получено соотношение между годовой процентной став-
кой и непрерывной
r
δ
:
(
)
T
T
re +=
⋅
1
δ
.
Откуда
1er
δ
=
+
или
(
)
r
+
=
1ln
δ
.
Например, при
15%
δ
= годовая ставка
0,15
1 1 0,1618 16,18%re e
δ
=−= −≈ = .
Простейшим примером долгосрочного страхования является полное
страхование жизни. Его называют также пожизненным страхованием на слу-
чай смерти. При этом виде страхования человек платит страховой компании
p
грн., а компания соглашается выплачивать наследникам застрахованного грн.
после его смерти.
b
В отличие от примеров краткосрочного страхования ни факт предъявле-
ния иска, ни его величина не содержат элемента неопределенности: застрахо-
ванный когда-то умрет и компания обязательно выплатит грн. За счет чего
она сможет получить эту сумму? Дело в том, что компания получает плату за
страховку
b
p
грн. в момент заключения договора, а выплату грн. производит
много позже.
b
Пусть возраст страхуемого
x
лет. Обозначим через его остаточное
время жизни. При непрерывно начисляемых процентах к моменту смерти ком-
пания будет иметь сумму
()Tx
()Tx
pe
δ
⋅
.
Доход компании от заключения договора
()Tx
p
eb
δ
ε
=
− .
Чтобы иметь сумму грн. в момент смерти застрахованного, страховая компа-
ния должна получить в момент заключения договора сумму
b
()Tx
zbe
δ
−
=⋅ (грн.)

198
Эта сумма выражает современную величину будущей страховой выплаты. Т.к.
эта сумма случайная, компания назначает в качестве нетто-премии ее матема-
тическое ожидание
{
}
()Tx
bM e
δ
−
⋅ .
Если размер страхового пособия принять в качестве условной денежной еди-
ницы (т.е. у.е.), то нетто-премия при полном страховании жизни равна
b
1b =
{
}
()fT
x
mMe
x
δ
−
=
(у.е.)
2. В расчетах при долгосрочном страховании жизни предполагают, что про-
должительность жизни описывается моделью де Муавра. Согласно этой модели
остаточное время жизни застрахованного имеет равномерное распределе-
ние на промежутке времени
()Tx
0 tx
ω
<< −, где
ω
– предельный возраст,
x
– воз-
раст на момент заключения договора.
Функция распределения остаточного времени жизни имеет вид:
0, 0
(() ) ,0
1,
t
t
PT x t t x
x
tx
ω
ω
ω
≤
⎧
⎪
⎪
<
=<≤
⎨
−
⎪
>−
⎪
⎩
−
Поскольку случайная величина принимает значения на ограниченном
промежутке
()Tx
(0; )
x
ω
− , то современная величина будущей страховой выплаты
принимает значения из промежутка . Функция распределения
случайной величины
()Tx
ze
δ
−
=
()
(
x
e
δω
−−
;1)
z
принимает следующие значения:
()
0Pz t<=, если
()
x
te
δω
−
⋅−
≤ ,
(
)
1Pz t
<
= , если . 1t ≥
Для имеем:
()
1
x
et
δω
−−
<<
()
()
()
()
()
()
1
ln ln
Tx
Pz t Pe t P Tx t PTx t
δ
δ
δ
−
⎛⎞
<= <= − < = >− =
⎜⎟
⎝⎠
()
()
ln
ln ln
111
t
tt
PTx
x
x
δ
δω δω
⎛⎞
−
⎜⎟
⎛⎞
⎝⎠
=− ≤− =− =+
⎜⎟
−
−
⎝⎠
.
В итоге, получим
()
()
()
()
0,
ln
1,
1, 1
x
x
te
t
Pz t e t
x
t
δω
δω
δω
−−
−−
⎧
≤
⎪
⎪
<=+ <<
⎨
−
⎪
⎪
≥
⎩
1
Соответственно, плотность распределения величины
z
:
()
()
()
()
()
()
1
, ,1
0, ,1
x
x
te
tx
fx
te
δω
δω
δω
−−
−−
⎧
∈
⎪
−
=
⎨
⎪
∉
⎩
Найдем нетто-премию при полном страховании жизни
f
x
m как математическое
ожидание случайной величины
z
:
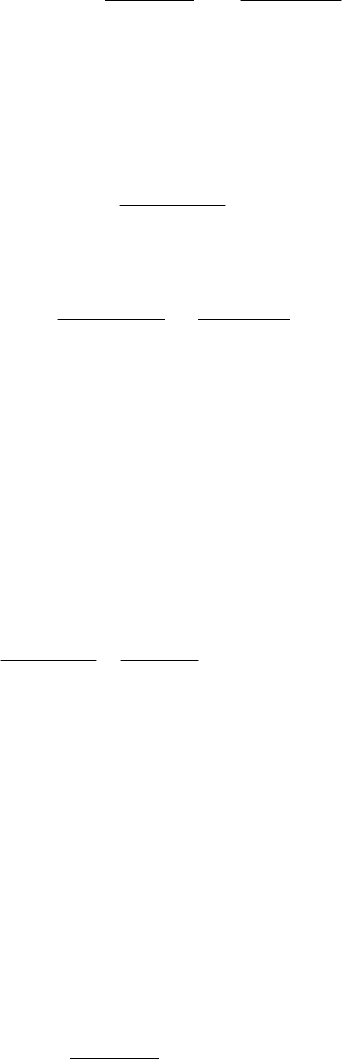
199
()
()
()
()
1
()
0
11
x
x
f
x
e
e
m Mz tf t dt dt
x
x
δω
δω
δω δω
−−
∞
−−
−
== = =
−−
∫∫
.
(1)
Как и ожидалось, нетто-премия монотонно возрастает при росте
x
и ста-
новится равной страховой выплате, если возраст на момент заключения догово-
ра
x
близок к предельному возрасту
ω
. Находя начальный момент 2-го порядка
2
M
z , получим
(
)
()
2
2
1
2
x
e
Mz
x
δω
δω
−−
−
=
−
.
Тогда дисперсия равна
() ()
2
2( ) ( )
22
11
()
2
xx
ee
Dz Mz Mz
x
x
δω δω
δω δω
−− −
⎛⎞
−−
=− = −
⎜⎟
⎜⎟
−−
⎝⎠
.
(2)
Пример 1. Подсчитать величину нетто-премии при заключении договора
полного страхования жизни для клиента в возрасте 30 лет, с предельным воз-
растом
80
ω
= лет, при годовой процентной ставке 60%r
=
и размером страхово-
го пособия грн.
1000b =
Решение. По годовой процентной ставке рассчитаем непрерывную про-
центную ставку:
()
(
)
ln 1 0,6 ln 1, 6 0, 47 47%
δ
=+= = =
Используя (1), найдём нетто-премию
50 0,47 23,5
30
11
0,0426
50 0,47 23,5
f
ee
m
−⋅ −
−−
===
⋅
(у.е.)
Умножив это число на грн., получим нетто-премию в реальных денеж-
ных единицах:
1000b =
30
0,0426 1000 42,6
f
m =⋅= (грн.)
3. Другим видом долгосрочного страхования является страхование жизни на
лет. При этом виде страхования выплата страхового пособия производится, ес-
ли застрахованный умер в течение срока действия договора, т.е. лет с момен-
та заключения договора. Если же застрахованный прожил эти лет, то компа-
ния не платит ничего. Для этого вида страхования нетто-премия для клиента в
возрасте
n
n
n
x
лет рассчитывается по формуле:
()
1
n
n
x
e
m
x
δ
ω
δ
−
−
=
−
.
(3)
Еще один вид страхования – -летнее смешанное страхование жизни.
Выплата страхового пособия производится на следующих условиях. Если
смерть застрахованного наступит до истечения срока действия договора, то
страховое пособие выплачивается в момент смерти. Если же застрахованный
дожил до окончания срока действия договора, то страховое пособие выплачи-
вается в момент окончания срока действия договора.
n
Этот вид выполняет как функции страхования, так и накопления средств.
Нетто-премия для застрахованного в возрасте
x
лет:
