Полшков Ю.Н. Курс лекций по экономико-математическому моделированию

Подождите немного. Документ загружается.

Заметим, что в пространстве

выполняется равенство

+=. Обо-

значим

= , тогда

λλ

=− . Поэтому выпуклая линейная комбинация имеет

вид

(1 )XX

− ,

где 01

≤≤.

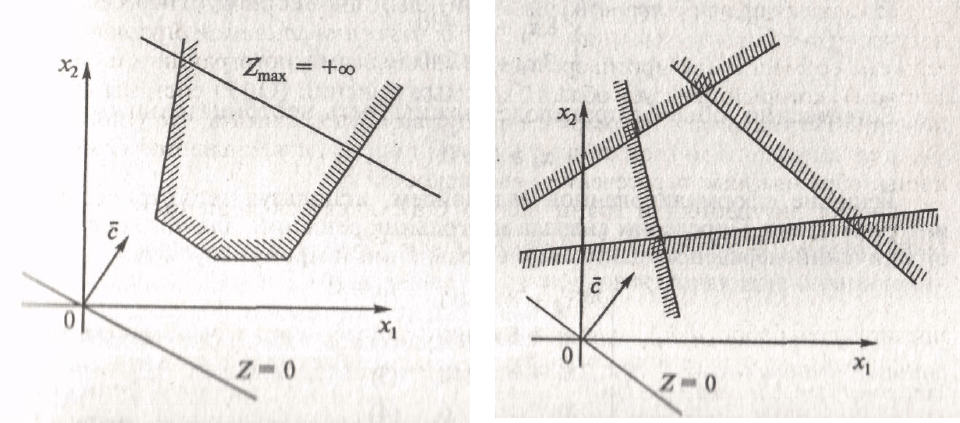
Принципиально другие ситуации рассмотрены на рис. 3. Так рис. 3, А)

изображает вариант, когда система ограничений образует неограниченное

сверху множество. Функция

при этом стремится к бесконечности. На рис. 3,

Б) представлен случай несовместной системы ограничений.

А) Б)

Рис. 3. Случаи отсутствия решения задач ЛП

Домашнее задание. Составить четыре конкретные задачи ЛП на мини-

мум, аналогичные ситуациям, рассмотренным на рис. 2 и 3.

Лекция 3. ПРАКТИЧЕСКАЯ РЕАЛИЗАЦИЯ ГРАФИЧЕСКОГО

МЕТОДА РЕШЕНИЯ ЗАДАЧ ЛИНЕЙНОГО

ПРОГРАММИРОВАНИЯ

План

1. Пример графического решения задачи ЛП.

2. Задачи ЛП, сводящиеся к графическому методу решения.

1. Рассмотрим графическое решение конкретной задачи ЛП.

Пример 1. Решить графически задачу ЛП:

42 maZx x x

+→ ,

2318

x x

−

+≤

⎧

⎪

+≤

⎪

⎨

−+≥−

⎪

−≥

⎩

0 0x,x≥≥

Решение. Для нахождения ОДР строим граничные прямые и определяем

полуплоскости, координаты точек которых удовлетворяют ограничениям.

Рассмотрим первое ограничение 93

≤

−

xx . Строим прямую :

по двум точкам

3xx−+ =9 0

x , 3

x и 9

−

x , 0

x . Берём контроль-

ную точку

, не лежащую на этой прямой, например, . Подставляем её ко-

ординаты в первое ограничение. Если неравенство в этой точке выполняется, то

первое ограничение определяет полуплоскость, которая содержит контрольную

точку, если же нет, то оно определяет полуплоскость, в которой не лежит кон-

трольная точка. В точке неравенство выполняется:

(0;0)O

(0;0)O 03009

−

+⋅=<. По-

этому первое ограничение определяет полуплоскость, расположенную ниже

прямой

. На рис. 1 это отмечено двумя стрелками.

Аналогично поступаем с остальными тремя ограничениями. Результаты

вычислений запишем в табл. 1.

Табл. 1. Вспомогательные расчёты

Пря-

мая

Уравнение

прямой

Точки на

прямых

Кон-

троль-

ная

точка

Знак нера-

венства в

этой точке

Принадлеж-

ность кон-

трольной точки

к ОДР

3xx−+ =9

(0,3) (

–9,0) О(0,0)

–0+3⋅0 <9

О принадлежит

l 1832

=+ xx

(0,6) (9,0) О(0,0)

⋅0+3⋅0 <18

О принадлежит

2xx−+=−10

(0,

–10) (5,0) О(0,0)

–2⋅0+0 >–10

О принадлежит

2xx−=0

(0,0) (1,2) М(0,5)

⋅0–5<0

М не принадл.

Выделяем ОДР – пятиугольник OABCD. Строим вектор

, пока-

зывающий направление наибольшего возрастания функции

(4,2)c =

. Строим изоцель

– прямую, перпендикулярную вектору

42xx0

= .

Т.к. мы ищем максимум целевой функции, то изоцель следует переме-

щать параллельными переносами в направлении вектора

, пока она не станет

опорной к ОДР (рис. 1). Это произойдёт в точке . Находим координаты

точки :

(; )Cx x

12 1

12 2

2318, 6

210,

xx x

x x x

⎧

⎧⎧

⇒⇒

⎨⎨ ⎨

−

⎩⎩

⎩

C(6,2)

0 D

Рис. 1. Иллюстрация графического метода

Найдено единственное оптимальное решение *(6;2)X

. Вычисляем зна-

чение целевой функции:

max

(*) 46 22 28ZZX==⋅+⋅=.

Ответ: , . *(2;6)X =

max

28Z =

Заметим, что в точке достигается минимум целевой функции, рав-

ный .

(0;0)O

min

0Z =

2. Мы научились применять графический метод для задач ЛП, которые содер-

жат две переменные

На самом деле, некоторые задачи ЛП, размерность которых превышает 2,

можно свести к задаче двух переменных. Остальные переменные при этом

должны быть исключены.

Пример 2. Решить задачу ЛП:

12345

16 5 5 maxZxxxxx=− − + + + → ,

123

12 4

12 5

2 10

23 6

2 4 8

xxx

xx x

⎧

⎪

−+ + =

⎨

⎪

−=

⎩

x ≥ ( 1, 5j = ).

Решение. Выразим неизвестные

345

xx из первого, второго и третьего

равенств системы ограничений соответственно:

10 2

62 3

82 4

=− −

⎧

⎪

=+ −

⎨

⎪

=− + +

⎩

(1)

Исключаем данные неизвестные из целевой функции:

12 12 1 2 1 2 1

16 (102 )5(62 3)5(82 4)2 3

xx xx x x x x x x=− − + − − + + − + − + + = +

Т.к. все переменные задачи – неотрицательные, то предыдущую систему ра-

венств запишем в виде системы неравенств:

10 2 0

62 3 0

82 4 0

−−≥

⎧

⎪

+−≥

⎨

⎪

−+ + ≥

⎩

248

+≤

⎧

⎪

−

+≤

⎨

⎪

≥

⎩

Получена задача ЛП:

23 maZxx=+→x

248

+≤

⎧

⎪

−

+≤

⎨

⎪

≥

⎩

0 0x,x≥≥

Решим её графическим методом.

Для данной задачи ОДР – заштрихованный четырёхугольник

BCD (рис.

2). Уравнение изоцели следующее:

23xx0

= .

Двигая изоцель параллельными переносами в направлении градиент-

вектора , достигнем опорной точки . Эта точка находится на

пересечении прямых I и II:

(2,3)c =

(; )Cx x

⎧

⎨

−+ =

⎩

⎧

⎨

⎩

При этом .

max

18Z =

Осуществим обратную замену, подставив координаты точки в

систему (1):

(3;4)C

⎧

⎪

⎨

⎪

⎩

Рис. 2. Графическое решение примера 2

Получено единственное оптимальное решение исходной задачи ЛП

. Подставив его в целевую функцию, убедимся в том, что * (3;4;0;0;14)X =

max

(*) 1634 0 5051418ZZX= =− ⋅−++⋅+⋅ = .

Ответ: , * (3;4;0;0;14)X =

max

18Z

Лекция 4. ТЕОРЕТИЧЕСКОЕ ОБОСНОВАНИЕ СИМПЛЕКС-

МЕТОДА

План

1. Различные формы задачи ЛП.

2. Симплексный метод решения задач ЛП.

1. Из геометрической интерпретации задачи линейной оптимизации видно, что

максимум или минимум целевой функции достигается в угловой точке выпук-

лого многогранника – ОДР. Поэтому в основу симплекс-метода положена идея

рассмотрения и испытания на оптимальность только угловых точек – вершин

многогранника. Сформулируем теоретические факты, на которых базируется

симплекс-метод.

Любая задача ЛП может быть приведена к каноническому виду:

11 2 2

min

Zcxcx cx

+ +⋅⋅⋅+ → , (1)

11 1 12 2 1 1

21 1 22 2 2 2

11 2 2

...............................................,

mm mnnm

ax ax ax b

+⋅⋅⋅+ =

⎧

⎪

+ +⋅⋅⋅+ =

⎪

⎨

⎪

++⋅⋅⋅+=

⎩

(2)

0( 1, )

jn≥=

. (3)

Рассмотрим матрицу-столбец переменных, матрицу-столбец свободных

членов, матрицу коэффициентов при неизвестных, матрицу-строку коэффици-

ентов целевой функции:

...

⎛⎞

⎜⎟

⎝⎠

, , ,

...

⎛⎞

⎜⎟

⎝⎠

11 12 1

21 22 2

...

... ... ... ...

...

mm mn

aa a

⎛⎞

⎜⎟

⎝⎠

(

)

...

Ccc c

Тогда каноническая задача ЛП (1)-(3) может быть записана в

матричной

форме

min

→ , (4)

, (5)

0X ≥ . (6)

Матрицу, с ст ящую из одного столбца или строки, ожно представлять

как вектор, т.е. ,

о о м

JJG

, . Введём дополнительно векторы C

( 1,

n= ), коорди-

наты которых – это

-е столбцы матрицы

. Тогда задача ЛП представима в

векторной форме:

min

⋅→

GJJG

, (7)

11 2 2

...

xAx AxB

⋅

+⋅++⋅=

JJGJJGJJGJG

, (8)

X ≥

JJG

. (9)

Планом задачи (допустимым решением) называют вектор , удовле-

творяющий условиям (2)-(3) или (5)-(6) или (8)-(9).

Оптимальный план – это

план, минимизирующий целевую функцию.

JJG

Рассмотрим векторную форму (7)-(9). Уравнение (8) – это разложение

вектора

по векторам

JJG

( 1,

n= ) с коэффициентами разложения

Напомним, что система векторов

( 1,

n= ) называется линейно неза-

висимой

, если равенство

11 2 2

... 0

AA A

μμ μ

⋅+⋅++⋅=

JJGJJGJJGG

выполняется только при одновременном равенстве нулю коэффициентов раз-

ложения, т.е.

... 0

μμ

====. В противном случае векторы называют линейно

зависимыми

Если векторы

, входящие в разложение (8) с положительными коэф-

фициентами

, являются линейно независимыми, то вектор называют

опорным планом. А т.к. векторы

JJG

имеют m координат, то количество

в опорном плане не может превышать число .

x >

Опорный план называют

невырожденным, если он содержит положи-

тельных компонент

. В противном случае он – вырожденный. Если все воз-

можные опорные планы задачи невырожденные, то это

невырожденная задача

ЛП. При наличии хотя бы одного вырожденного опорного плана задачу назы-

вают

вырожденной.

2. Рассмотрим некоторые свойства задачи ЛП.

Теорема 1. Множество всех планов задачи ЛП выпукло.

В общем случае ОДР либо пустая, либо является выпуклым многогран-

ным множеством.

Теорема 2. Пусть ОДР представляет собой выпуклый ограниченный мно-

гогранник в пространстве

. Тогда целевая функция принимает своё мини-

мальное (или максимальное) значение в одной из угловых точек. Если же целе-

вая функция принимает своё экстремальное значение более чем в одной угло-

вой точке, то экстремум достигается на всей выпуклой комбинации этих точек.

Каноническая задача ЛП в векторной форме (7)-(9) имеет свои специфи-

ческие особенности.

Теорема 3. Если векторы

, ,...,

JGJJGJJG

являются линейно независимыми и

имеет место разложение

11 2 2

...

xAx AxB⋅+ ⋅++ ⋅ =

JJGJJGJJGJG

∈

где все 0, то точка будет угловой точкой ОДР.

x ≥

( , ,..., ,0,0,...,0)

Xxx x R=

Теорема 4. Если является угловой точкой ОДР, то векторы

(, ,..., )

Xxx x=

JJG

из разложения (8), соответствующие положительным коэффициентам

образуют линейно независимую систему.

Следствие 1 (из теорем 3 и 4). Если в задаче (7)-(9) векторы

JJG

имеют

координат, то угловые точки ОДР

(, ,..., )

Xxx x

содержат не более положи-

тельных координат, а остальные равны нулю.

Решение задачи ЛП (7)-(9) становится более удобным, если среди -

мерных векторов

, ,...,

JJGJJGJJG

имеется единичных векторов m

...

⎛⎞

⎜⎟

⎝⎠

JJG

, ,…, .

...

⎛⎞

⎜⎟

⎝⎠

JJG

...

⎛⎞

⎜⎟

⎝⎠

JJG

Т.к. эти векторы линейно независимы и их количество совпадает с размерно-

стью пространства, то данные векторы образуют

базис пространства

Рассмотрим произвольный вектор из разложения (8):

...

⎛⎞

⎜⎟

⎝⎠

JJG

Этому вектору соответствует переменная

и коэффициент целевой функ-

ции. Вектор

JJG

допускает единственное разложение в единичном базисе

11 2 2

...

jmmjj

aAa AaA

⋅

+⋅ ++⋅ =

JJGJJGJJGGJJ

, (10)

которому соответствует единственное значение целевой функции

11 12

...

jmmj

ca ca c a z⋅+⋅++⋅=

. (11)

Теорема 5. Пусть является опорным планом задачи (7)-

(9). Если для некоторого вектора

112

( , ,..., )

Xxxx=

выполняется условие , то данный

опорный план не будет оптимальным и можно построить другой опорный план

, для которого .

zc−>

() (zX zX< )

Заметим, что опорный план является лучшим по сравнению с .

Критерий

zc−

из (10) и (11) называют оценками оптимальности. Если для

некоторого опорного плана разложения всех векторов

(

n= ) в данном ба-

зисе удовлетворяют условию

−

≤

, то данный план является оптимальным.

С учётом всего сказанного,

симплексный метод – это метод последова-

тельного улучшения плана при решении задачи ЛП.

Симплекс-метод впервые предложил в 1947 г. американский математик

Дж. Данциг. Название метода происходит от английского слова «simple» – про-

стейший. Это связано с тем, что на начальном этапе развития метода, ОДР име-

ли простейший вид. Например, ОДР представляла собой пирамиду в простран-

стве

с вершинами , (0;0;0)O (1;0;0)

, (0;1;0)

и . Эту пирамиду

иногда называют симплексом.

(0;0;1)C

Лекция 5. СИМПЛЕКС-МЕТОД РЕШЕНИЯ ЗАДАЧ

ЛИНЕЙНОЙ ОПТИМИЗАЦИИ

План

1. Пример решения задачи ЛП с помощью симплекс-метода.

2. Алгоритм симплекс-метода.

1. Рассмотрим решение конкретной задачи ЛП с помощью симплекс-метода.

Пример 1. Для выпуска двух видов продукции по цене 2 грн. и 3 грн. ис-

пользуется три вида сырья с запасами 60 кг, 54 кг, 60 кг. Расходы сырья на еди-

ницу продукции первого вида соответственно равны 3; 1; 2 кг, второго — 2; 3; 3

кг, соответственно. Данные сведены в табл. 1.

Табл. 1. Данные задачи

Продукция (расходы сырья на еди-

ницу продукции)

Сырьё

Запасы

сырья

3 кг 2 кг 60 кг

1 кг 3 кг 54 кг

2 кг 3 кг 60 кг

Цена единицы продукции 2 грн. 3 грн.

Количество продукции

Найти план выпуска продукции, чтобы доход от её реализации был мак-

симальный.

Решение. Обозначим через

количество выпуска продукции первого

вида,

– второго вида,

– доход от реализации всей продукции. Тогда мате-

матическая модель задачи ЛП принимает вид:

23 maZx x x

+→ , (1)

3260

354

2360

x ,

+≤

⎧

⎪

+≤

⎨

⎪

+≤

⎩

(2)

0 0x,x≥≥

. (3)

Приведём задачу (1)-(3) к каноническому виду. При наличии ограниче-

ния-неравенства прибавляем или вычитаем в левой части дополнительную (ба-

лансовую) неотрицательную переменную, чтобы преобразовать его в равенство.

Равенства оставляем без изменения. Если задача на минимум, то целевую

функцию оставляем без изменения, если на максимум, то делаем замену

−=

′

. Кроме того, для применения симплекс метода нужно, чтобы правые

части ограничений (2) были неотрицательными.

12345

230 0 0 miZZ xx x x x n

′

−=− − +⋅ +⋅ +⋅ → , (4)

123

12 4

12 5

32 60

23 60

x x ,

x x x ,

x x ,

++ =

⎧

⎪

++=

⎨

⎪

++=

⎩

(5)

0( 1,5)

x j≥=

. (6)

Запишем систему ограничений (5) в векторном виде:

1234

12 3 4 5

xA xA xA xA xA=⋅ +⋅ +⋅ +⋅ +⋅

, (7)

где

1 2345

60 3 2 1 0 0

54, 1, 3, 0, 1, 0 .

60 2 3 0 0 1

BAAAAA

⎛ ⎞ ⎛⎞ ⎛⎞ ⎛⎞ ⎛⎞ ⎛⎞

⎜ ⎟ ⎜⎟ ⎜⎟ ⎜⎟ ⎜⎟ ⎜⎟

= = ====

⎜ ⎟ ⎜⎟ ⎜⎟ ⎜⎟ ⎜⎟ ⎜⎟

⎝ ⎠ ⎝⎠ ⎝⎠ ⎝⎠ ⎝⎠ ⎝⎠

(8)

Равенство (7) является разложением вектора

по векторам

1 2345

, , , , .

AAAA

Векторы (8) являются 3-х мерными. Поэтому за базис этой системы век-

торов можно взять систему единичных векторов

(

)

345

, , Б AAA= . Свободные

переменные приравниваем к нулю:

0 0x,x

= . Значения базисных перемен-

ных находим из системы (5):

345

60 54 60x,x, x

==. Эти числа означают коли-

чество неиспользованного сырья. Базисное решение будет определять началь-

ный опорный план, т.к. базисные переменные принимают положительные зна-

чения:

(

)

(

)

0 0 60 54 60 2 0 3 0 0 60 0 54 0 60 0

ББ

X,,,,, Z X

′

= =−⋅−⋅+⋅ +⋅ +⋅ =.

Т.к. продукция не выпускается, то доход от реализации равен нулю (

= ).

Симплексная таблица (табл. 2) составляется следующим образом. В пер-

вой строке шапки симплекс-таблицы указаны векторы системы ограничений

(5), а во второй – коэффициенты при переменных в целевой функции. В первом

столбце (столбец ) указаны векторы, образующие базис заданной системы

векторов, а во втором столбце – коэффициенты целевой функции при базисных

переменных. Во всех остальных клетках таблицы (кроме последней строки, о

которой будет сказано ниже) стоят коэффициенты разложения соответствую-

щих векторов по векторам базиса. Т.к. для нашей задачи выбран единичный ба-

зис, то в первой симплексной таблице в столбцах

11 234

, , , , ,

AAAAA будут

стоять координаты векторов (8).

Последняя строка называется

индексной. В третьем столбце этой строки

стоит значение целевой функции при проверяемом опорном плане

(

)

Z X

′

а во всех остальных клетках индексной строки стоят оценки оптимальности

для векторов исходной системы.

cz −

В первой симплексной таблице имеем:

(

)

Z X СВ

′

=⋅ = 0⋅60+0⋅54+0⋅60 = 0, z

–c

С A

⋅

= 0⋅3+0⋅1+0⋅2– (–2) =2,

–c

= 0⋅2+0⋅3+0⋅3– (–3) = 3, z

–c

= 0⋅1+0⋅0+0⋅0–0 = 0,