Полшков Ю.Н. Курс лекций по экономико-математическому моделированию
Подождите немного. Документ загружается.

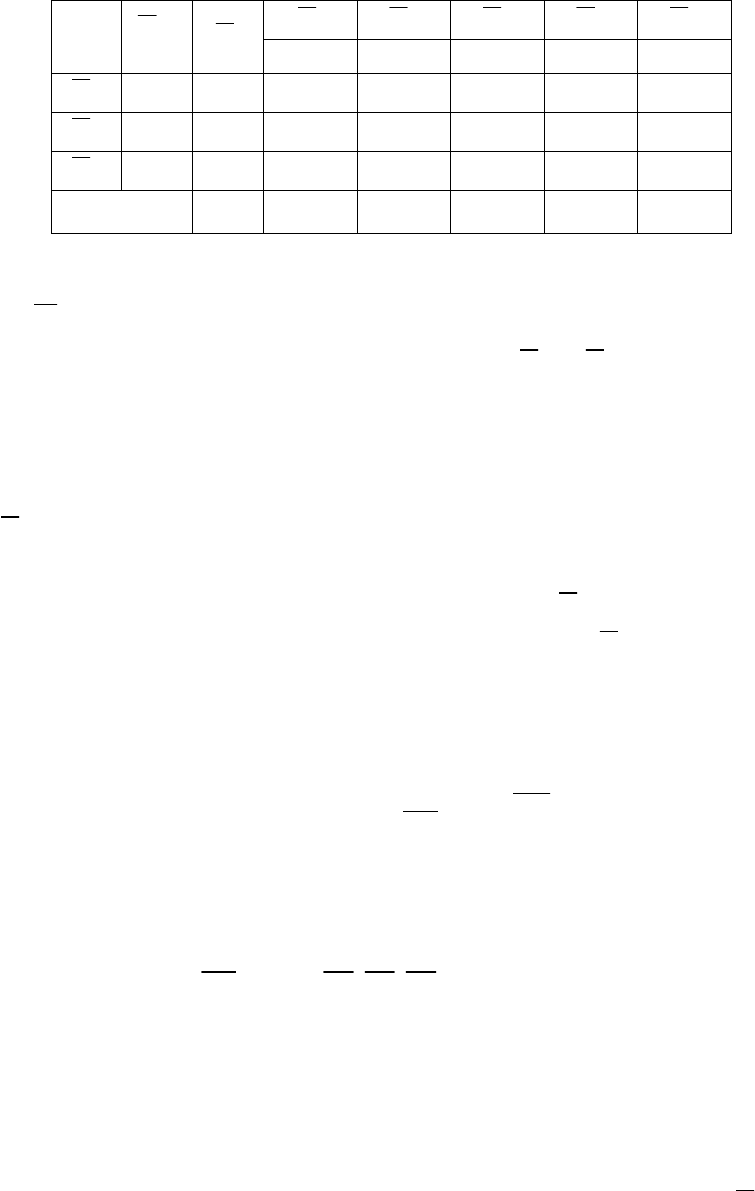
20
z
4
–c
4
= 0⋅0+0⋅1+0⋅0–0 = 0, z
5
–c
5
= 0⋅0+0⋅0+0– 0 = 0.
Результаты вычислений помещаем в табл. 2.
Табл. 2. Первая симплексная таблица
1
À
2
À
3
À
4
À
5
А
1
Б
1
Б
С
1
В
–2 –3 0 0 0
3
À
0 60 3 2 1 0 0
4
À
0 54 1 3 0 1 0
5
À
0 60 2 3 0 0 1
jj
cz −
0 2 3 0 0 0
Воспользуемся теоремой 5 из предыдущей лекции. Проверяемый опор-
ный план
(
)
1
00605460
Б
X,,,,= не является оптимальным, т.к. в индексной стро-
ке имеются положительные оценки для векторов
1
À
и
2
А
. Перейдём к новому
опорному плану, выбрав новый базис. Базис не может содержать более трёх
векторов. Поэтому введём в него один из свободных векторов, выведя один из
базисных.
Вводить следует вектор с наибольшей оценкой оптимальности. Это будет
вектор
2
А
, для которого . Число 3 означает, что если переменную
22
3zc−=
2
x
увеличить на единицу, то целевая функция уменьшится на 3 единицы и прибли-
зится к минимуму. В этом отношение ввод вектора
1
А
даст меньший эффект,
т.к. . Столбец с вводимым в базис вектором
11
2zc−=
2
А
называют направ-
ляющим
и выделяем жирной линией и стрелкой.
Для определения вектора, выводящегося из базиса, вычисляют
наимень-
шее симплексное отношение
0
0
min , 1,
i
j
ij
ij
a
b
i
a
θ
>
⎧⎫
⎪⎪
=
⎨⎬
⎪⎪
⎩⎭
m=
, (9)
где
j
– номер вектора, вводимого в базис.
В данном случае 2
j
= , поэтому
{}
02
2
2
0
60 54 60
min min min 30 18 20 18
233
i
i
i
a
b
,, ,,
a
θ
>
⎧⎫
== =
⎨⎬
⎩⎭
=
.
Симплексные отношения означают возможные объёмы производства
продукции из имеющихся запасов сырья. Наименьшее симплексное отноше-
ние означает максимально возможный выпуск этой продукции. Действительно,
запасы сырья позволяют изготовить не более 18 единиц продукции , в то
время как сырьё 1-го вида – 30 единиц, а 3-го – 20 единиц.
2
P
2
S
2
P
Наименьшее симплексное отношение соответствует вектору
4
À
, значит,
этот вектор будет выведен из базиса. Он расположен в т.н.
направляющей
строке
, которую выделим жирной линией и стрелкой. На пересечении направ-

21
ляющей строки и направляющего столбца находится
разрешающий элемент
, выделяемый квадратными скобками (табл. 3).
22
3a =
Табл. 3. Первая симплексная таблица с комментариями
↓
1
À
2
À
3
À
4
À
5
А
θ
1
Б
1
Б
С
1
В
–2 –3 0 0 0
3
À
0 60 3 2 1 0 0 60/2=30
←
4
À
0 54 1
[3]
0 1 0 54/3=18
–
2/3
–
1
5
À
0 60 2 3 0 0 1 60/3=20
jj
cz −
0 2 3 0 0 0
Новый базис
(
)
325
2
, , Б AAA= обуславливает необходимость пересчёта
симплексной таблицы. Элементы направляющего столбца (за исключением
разрешающего) должны быть преобразованы в нули, а сам разрешающий эле-
мент должен стать единицей. Для этого применяют
правило полных жорда-
новых исключений
.
Рекомендуем воспользоваться двумя
элементарными преобразования-
ми Гаусса
: 1) направляющую строку умножаем на подходящее число и при-
бавляем к другой строке; 2) направляющую строку делим на разрешающий
элемент.
Необходимые пояснения помещены в табл. 3. Например, чтобы получить
0 на месте элемента , умножим направляющую строку на (–2/3)
и приба-
вим к первой строке. Получим:
12
2a =
60 3
2 1 0 0 первая строка
+
–36 –2/3
–2 0 –2/3 0 направл. строка, умноженная на (–2/3)
24 7/3
0 1 –2/3 0 результат сложения
Результаты вычислений поместим в табл. 4.
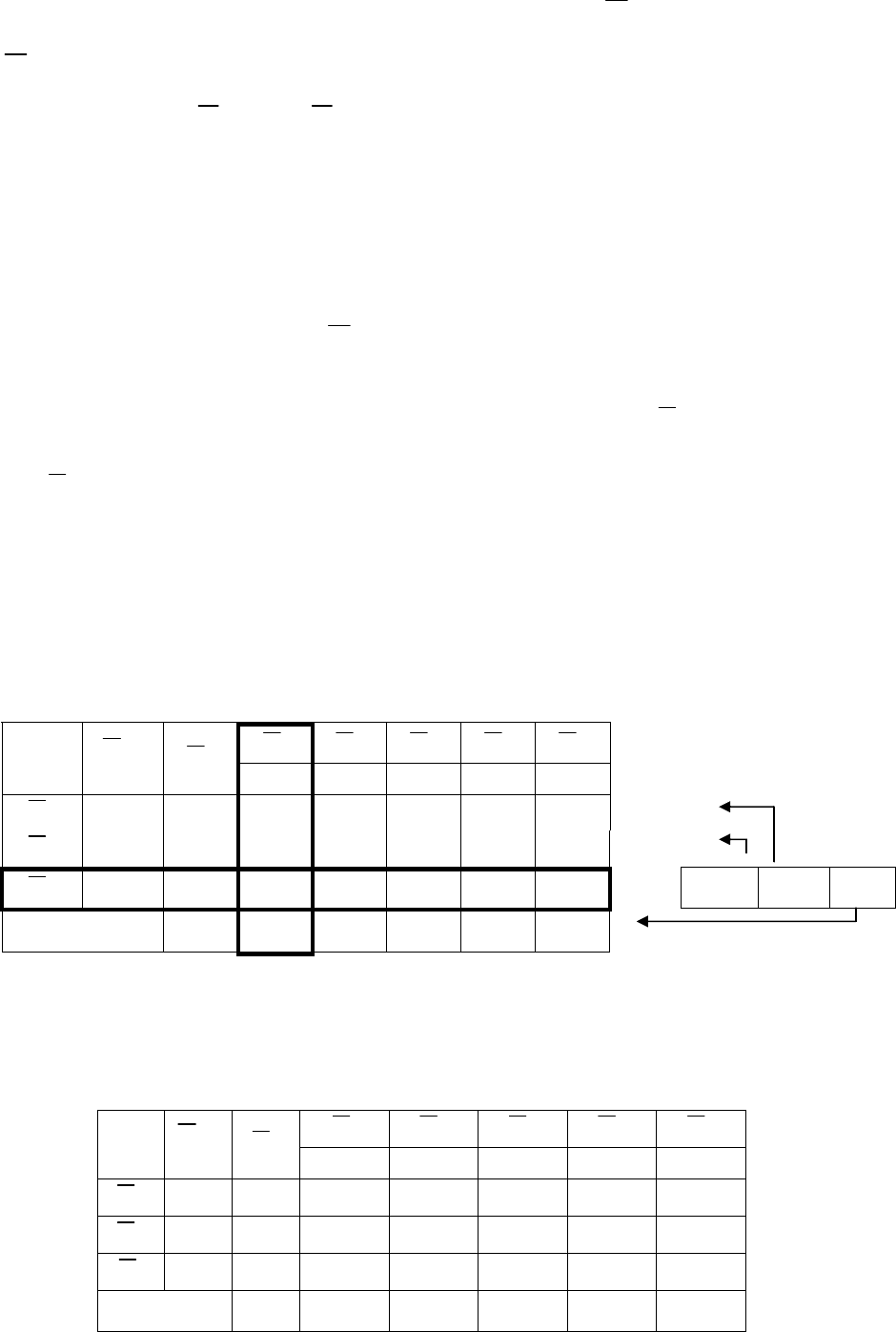
Табл. 4. Вторая симплексная таблица
1
À
2
À
3
À
4
À
5
À
2
Б
2
Б
С
2
В
–2 –3 0 0 0
3
À
0 24 7/3 0 1 –2/3 0
2
À
–3 18 1/3 1 0 1/3 0
5
À
0 6 1 0 0 –1 1
jj
cz −
–54 1 0 0 –1 0
22
Заполнение второй симплекс-таблицы завершаем первую итерацию алго-
ритма симплексного метода. Имеем опорный план
()
2
0182406
Б
X,,,= , при
(
)
2
54
Б
Z X
′
=−
. Обратим внимание на следующий факт:
(
)
(
)
2202
21
( ) 0 3 18 54
ББ
Z X Z X z с
θ
′′
= −−⋅=−⋅=−
.
Т.е. уменьшение значения целевой функции (а, значит, и улучшение опорного
плана) произошли за счёт оценки оптимальности
22
3zc
−
= и наименьшего
симплексного отношения
02
18
θ
=
.
Повторяем действия, совершаемые при первой итерации.
В индексной строке есть положительная оценка оптимальности
11
1zc
−
=
.
Следовательно, опорный план
2
Б
X не является оптимальным. Необходим пе-
реход к новому опорному плану. Положительная оценка оптимальности един-
ственная и, значит, наибольшая. Ей соответствует вектор
1
À
, который будем
вводить в базис. Рассчитав наименьшее симплексное отношение, получим, что
вектор
5
А
следует выводить из базиса. Отмечаем направляющие строку и стол-
бец, разрешающий элемент, вносим необходимые пояснения, применяем пра-
вило полных жордановых исключений.
Итоги сведём в табл. 5.
Табл. 5. Вторая симплексная таблица с комментариями
↓
1
À
2
À
3
À
4
À
5
À
θ
2
Б
2
Б
С
2
В
–2 –3 0 0 0
3
À
0 24 7/3 0 1 –2/3 0 72/7
2
À
–3 18 1/3 1 0 1/3 0 54
←
5
À
0 6
[1]
0 0 –1 1 6 –1/3 –7/3 –1
jj
cz −
–54 1 0 0 –1 0
После расчётов и преобразований получим табл. 6.
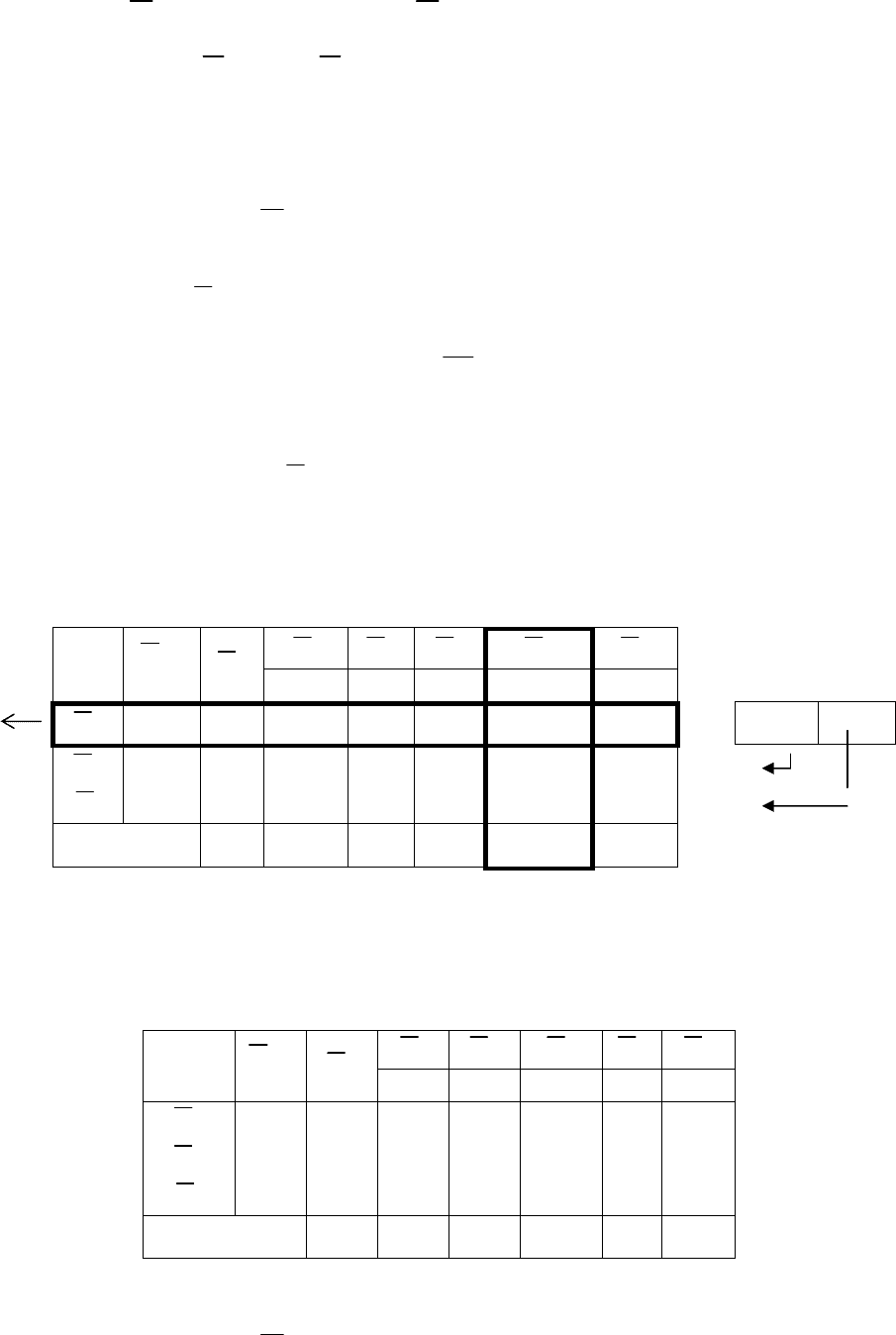
Табл. 6. Третья симплексная таблица
1
À
2
À
3
À
4
À
5
À
3
Б
3
Б
С
3
В
–2 –3 0 0 0
3
À
0 10 0 0 1 5/3 –7/3
2
À
–3 16 0 1 0 2/3 –1/3
1
À
–2 6 1 0 0 –1 1
jj
cz −
–60 0 0 0 0 –1
23
Имеем:
(
)
(
)
3
6161000 ; 60
3
ББ
X ,,,, Z X Z
∗
=
′′
==− или
()()
1101
32
() 5416
ББ
Z X Z X z с
θ
′′
= −−⋅=−−⋅=−60.
Т.к. в индексной строке находятся только отрицательные и нулевые эле-
менты, то третий опорный план оптимальный, а значение целевой функции ми-
нимальное:
()
1
min
6161000 ; 60Х ,,,, Z
∗
′
==−.
Полученное оптимальное решение не является единственным, потому что
свободный вектор
4
À
имеет нулевую оценку. Введём его в базис. Рассчитаем
симплексные отношения. Одно из них
6
6
1
⎛⎞
=
−
⎜
−
⎝⎠
⎟
получилось отрицательным. В
столбце
θ
ставим прочерк и не принимаем его во внимание. Среди положи-
тельных симплексных отношений 6 и 24 определяем наименьшее. Значит надо
выводить из базиса вектор
3
А
(табл. 7).
Табл. 7. Третья симплексная таблица с комментариями
↓
1
À
2
À
3
À
4
À
5
À
θ
3
Б
3
Б
С
3
В
–2 –3 0 0 0
3
À
0 10 0 0 1
[5/3]
–7/3 6 –2/5 3/5
2
À
–3 16 0 1 0
2/3 –1/3 24
1
À
–2 6 1 0 0
–1 1 –
jj
cz −
–60 0 0 0
0 –1
Проделав необходимые вычисления, получим табл. 8.
Табл. 8. Четвёртая симплексная таблица
1
À
2
À
3
À
4
À
5
À
4
Б
4
Б
С
4
В
–2 –3 0 0 0
4
À
0 6 0 0 3/5 1 –7/5
2
À
–3 12 0 1 –2/5 0 3/5
1
À
–2 12 1 0 3/5 0 –2/5
jj
cz −
–60 0 0 0 0 –1
Получаем альтернативный оптимальный план:
()
2
min
1212060 ; 60Х ,,,, Z
∗
′
==−.
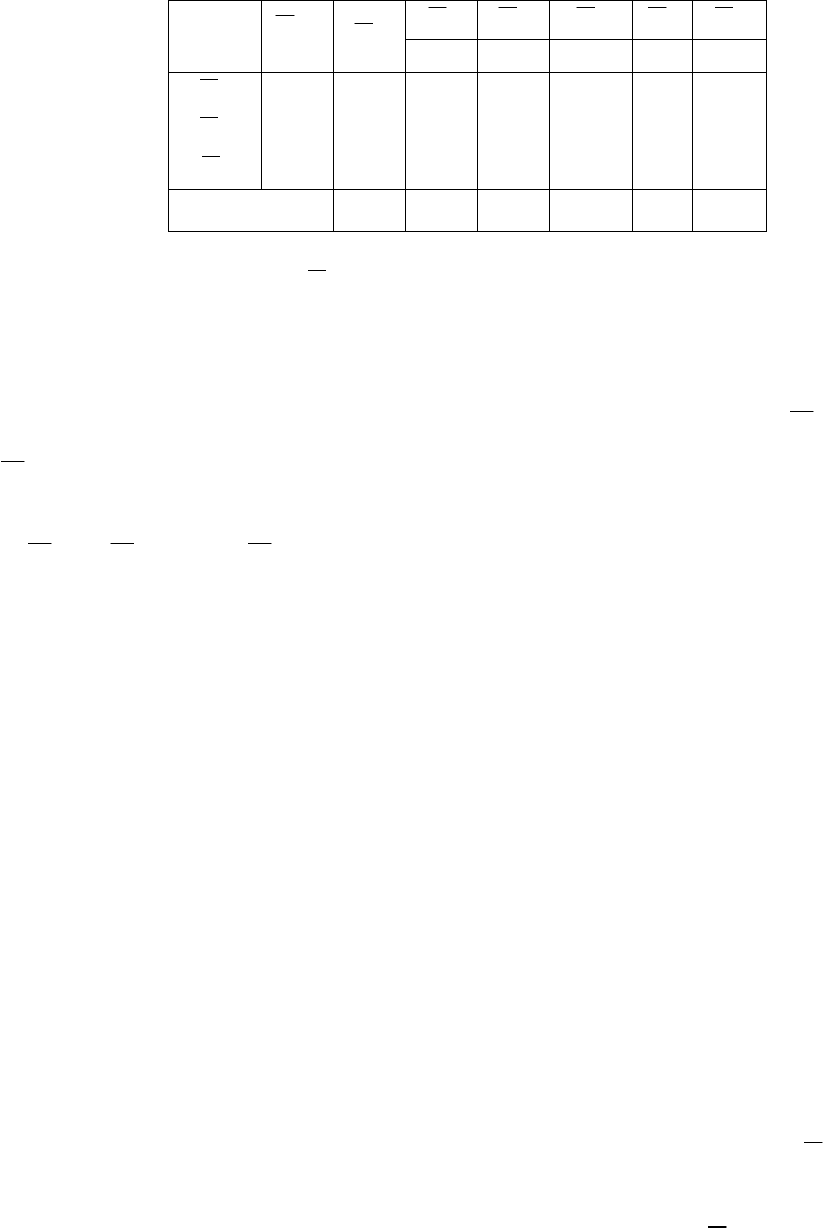
24
Добавив в табл. 8 пояснения, получаем табл. 9.
Табл. 9. Четвёртая симплексная таблица с комментариями
↓
1
À
2
À
3
À
4
À
5
À
4
Б
4
Б
С
4
В
–2 –3 0 0 0
θ
←
4
À
0 6 0 0
[3/5]
1 –7/5 10
2
À
–3 12 0 1 –2/5 0 3/5 –
1
À
–2 12 1 0 3/5 0 –2/5 20
jj
cz
−
–60 0 0 0 0 –1
Свободный вектор
3
À
имеет нулевую оценку, поэтому если ввести его в
базис, то получим оптимальный опорный план. Но при введении его в базис,
мы возвращаемся к предыдущему базису. Поэтому других оптимальных опор-
ных планов не будет.
Итак, найдены два оптимальных опорных решения:
1
(6;16) Х
∗
= и
2
(12;12)Х
∗
= . Поэтому оптимальным решением будет выпуклая линейная ком-
бинация данных решений:
()
12
(1 ) (6;16) (1 )(12,12) 12 6 ;12 4Х Х Х
λ
λλ λ λλ
∗∗ ∗
=+− = +− =− + 0 1 ,
λ
≤≤.
Исходная задача предполагала поиск максимума целевой функции. По-
этому
.
max
60 Z =
Задача ЛП решена полностью.
2. Обобщим описанные выше вычислительные процедуры.
Приведём
алгоритм симплексного метода и замечания к нему:
1) Задачу ЛП записываем в каноническом виде с неотрицательными пра-
выми частями ограничений.
2) Находим опорное решение (в каждом уравнении должна быть пере-
менная с коэффициентом единица, которая входит только в одно уравнение).
3) Составляем симплексную таблицу. Проверяем знаки . Если все
, то оптимальное решение найдено и определён минимум
jj
cz −
0≤−
jj
cz
Z
. Если же
имеются 0, то составляем новую симплексную таблицу и опять прове-
ряем знаки чисел в индексной строке. Итерации продолжаем до тех пор, пока
не получим в индексной строке все неотрицательные числа. Новую симплекс-
ную таблицу пересчитываем по правилу полных жордановых исключений.
>−
jj
cz
Замечание 1. Если в оптимальном плане свободный вектор
j
À
имеет ну-
левую оценку и среди чисел есть положительные, то оптимальный план не
единственный (может быть вырожденным). Вводя в базис
ij
a
′
j
À
, найдем ещё одно

25
оптимальное опорное решение. Если на некотором этапе возникнет -й стол-
бец с членами 0
и оценкой
j
ij
a
′
≤ 0>
−
jj
cz , то
−
∞→Z.
Замечание 2. Разрешающий столбец можно выбирать по положительной,
но не наибольшей оценке оптимальности. Иногда это упрощает вычисления и
даже уменьшает количество итераций. Например, в базис можно включать век-
тор, которому соответствует
(
)
0
max
jj j
zc
θ
⎡
⎤
−
⎣
⎦
, 0
jj
zc
−
> . Число
0 j
θ
опреде-
ляется для каждого .
j
Замечание 3. Если ОДР неограниченная, то могут быть решения, кото-
рые не являются выпуклой линейной комбинацией опорных решений.
Домашнее задание. Заводской цех выпускает 4 вида деталей, для произ-
водства которых использует сырьё, материалы и комплектующие изделия. Для
выпуска деталей 1-го вида требуется 2 ед. сырья и 2 ед. комплектующих, 2-го
вида – 2 ед. сырья, 1 ед. материалов и 1 ед. комплектующих, 3-го вида – 4 ед.
сырья и 2 ед. материалов, 4-го вида – 5 ед. сырья, 2 ед. материалов и 6 ед. ком-
плектующих. Производственные запасы имеются в количестве 28 ед. сырья, 10
ед. материалов и 14 ед. комплектующих изделий. Прибыль цеха от продажи од-
ной детали 1-го вида составляет 2 тыс. грн., 2-го вида – 4 тыс. грн., 3-го вида – 6
тыс. грн. и 4-го вида – 1 тыс. грн. Необходимо спланировать выпуск продукции
таким образом, чтобы прибыль от реализации выпущенных деталей была наи-
большей.
Ответ:
()
22;104;2;0Х
λ
λλ
∗
=+ − , 0 1
λ
≤
≤ .
Указание: 1) составить математическую модель задачи ЛП; 2) записать
задачу ЛП в каноническом виде; 3) решить задачу симплекс-методом.
26
Лекция 6. ДВОЙСТВЕННОСТЬ В ЛИНЕЙНОЙ
ОПТИМИЗАЦИИ
План
1. Двойственные задачи ЛП.
2. Теоремы двойственности.
1. Рассмотрим пример, который позволит нам с прикладной точки зрения по-
дойти к проблеме двойственности задач ЛП.
Пример 1. Фирма выпускает два вида сухих строительных смесей по це-
не 4 тыс. грн. и 5 тыс. грн. за 1 т. Для производства используется три вида сы-
рья с запасами 15 т, 7 т, 12 т, соответственно. Изготовление тонны 1-й смеси
требует 0,25 т сырья первого вида, 0,25 т сырья второго вида и 0,5 т сырья
третьего вида. На производство тонны 2-й смеси требуется 0,6 т сырья первого
вида, 0,2 т сырья второго вида и 0,2 т сырья третьего вида. Данные сведены в
табл. 1.
Табл. 1. Данные задачи
Продукция (расходы сырья на про-
изводство 1 т смеси)
Сырьё
1
P
2
P
Запасы
сырья
1
S
0,25 т 0,6 т 15 т
2
S
0,25 т 0,2 т 7 т
3
S
0,5 т 0,2 т 12 т
Цена за 1 т продукции 4 тыс. грн. 5 тыс. грн.
Количество продукции, т
1
x
2
x
Найти план выпуска продукции, чтобы доход от её реализации был мак-
симальный.
Решение. Обозначим через х
1
количество выпуска продукции первого
вида, х
2
– второго вида, Z – доход от реализации всей продукции. Тогда матема-
тическая модель задачи имеет вид:
12
12
12
12
12
45 ma
0, 25 0,6 15
0, 25 0, 2 7
0,5 0, 2 12;
00.
Zx x x;
x
x,
x
x,
x x
x,x
=
+→
+≤
⎧
⎪
+≤
⎨
⎪
+≤
⎩
≥≥
(1)
Приведя задачу (1) к каноническому виду, решим её симплекс-методом
(студентам проделать самостоятельно). Получим оптимальный план:
*
1
12x
=
т;
т; тыс. грн.
*
2
20x =
max
148Z =
Рассмотрим данную ситуацию в других экономических условиях. Купив
сырьё, фирма была уведомлена, что постоянный покупатель строительных сме-
27
сей разорился, а быстро организовать сбыт смесей затруднительно. Другая
фирма, производящая смеси, согласна купить сырьё. Необходимо договориться
о таких ценах на сырьё, которые бы устраивали обе стороны.
Обозначим цену в тыс. грн. за 1 т для сырья трёх видов, соответственно,
через , , . Т.к. для изготовления 1-й смеси используют разное сырьё в
объёмах 0,25 т, 0,25 т и 0,5 т, соответственно, то фирму-продавца устраивает
соотношение
1
y
2
y
3
y
123
0,25 0,25 0,5 4yyy
+
+≥, т.е. суммарная оплата компонент 1-й
смеси будет не менее 4 тыс. грн. за тонну. Аналогично определим и второе не-
равенство .
123
0,6 0, 2 0, 2 5yyy++≥
3
y
Фирма-покупатель стремится уменьшить расходы на приобретение сы-
рья, т.е. обеспечить минимум для целевой функции
12
15 7 12Fyy
=
++ . По-
этому математическая модель для новой ситуации будет следующей:
12 3
123
123
123
15 7 12 min;
0,25 0,25 0,5 4,
0,6 0,2 0,2 5;
000.
Fyy y
yyy
yyy
y,y,y
=++→
+
+≥
⎧
⎨
++≥
⎩
≥≥≥
(2)
Приведя задачу (2) к каноническому виду, решим её симплекс-методом
(студентам проделать самостоятельно). Получим оптимальный план:
тыс. грн.; тыс. грн.;
*
1
4,5y =
*
2
11,5y =
*
3
0y
=
тыс. грн.;
min
148F
=
тыс. грн. Как видно,
фирма-продавец получает одинаковый доход 148 тыс. грн. в обеих ситуациях.
Фирма-покупатель получает сырьё в полном объёме.
Задачи (1) и (2) называют
симметричной парой двойственных задач
ЛП
. Их структуры имеют однозначную связь (табл. 2). В качестве исходной
рассмотрена задача ЛП самого общего вида. Среди ограничений встречаются
как неравенства, так и равенства. Часть переменных произвольного знака.
Табл. 2. Симметричная пара
Исходная задача Двойственная задача
1
max
n
jj
j
Zcx
=
=→
∑
,
11
1
1
1
, 1, , ,
, 1, ,
n
ij j i
j
n
ij j i
j
ax b i m m m
ax b i m m
=
=
⎧
≤= ≤
⎪
⎪
⎨
⎪
==+
⎪
⎩
∑
∑
11
0, 1, ,
j
x
jnn≥= ≤n,
j
x
произвольного знака при
1
1,
j
nn=+
.
1
min
m
ii
i
Fby
=
=→
∑
,
11
1
1
1
, 1, , ,
, 1, ,
m
ij i j
i
m
ij i j
i
ay c j n n n
ay c j n n
=
=
⎧
≥= ≤
⎪
⎪
⎨
⎪
==+
⎪
⎩
∑
∑
11
0, 1, ,
i
yimm≥= ≤m,
i
y произвольного знака при
1
1,im m=+ .

28
2. Важную роль играют т.н. теоремы двойственности.
Первая теорема двойственности. Если одна из задач двойственной пары
имеет оптимальное решение, то и другая задача имеет оптимальное решение,
причём экстремальные значения целевых функций совпадают:
**
11
nm
jj ii
ji
cx by
==
=
∑∑
.
Если же целевая функция одной из задач не ограничена, то ОДР другой задачи
пустая.
Действительно, для примера 1 выполняется:
max
4 12 5 20 148Z
=
⋅+⋅= ,
min
15 4,5 7 11,5 12 0 148F =⋅ +⋅ +⋅= ,
max min
Z
F
=
.
Вторая теорема двойственности. Если в оптимальном плане исходной
задачи какая-то переменная (
*
0
j
x > 1,
j
n= ), то
j
-е ограничение двойственной
задачи её оптимальным решением обращается в строгое равенство. Если опти-
мальное решение исходной задачи обращает какое-то -е (
i
1,i= m
≥
) ограничение
в строгое равенство, то в оптимальном решении двойственной задачи .
*
0
i
y >
Рассмотрим выполнение первого утверждения этой теоремы на примере
1. Т.к. , то первое ограничение двойственной задачи
должно обращаться её оптимальным решением
в строгое равенство. Действительно,
*
1
0x >
123
0,25 0,25 0,5 4yyy++
*
(4,5;11,5;0)Y =
JG
0,25 4,5 0, 25 11,5 0,5 0 4⋅+ ⋅ +⋅=
.
Для :
*
2
0x >
0,6 4,5 0, 2 11,5 0, 2 0 5⋅+⋅ +⋅=.
Проверим выполнение второго утверждения теоремы. Оптимальное ре-
шение исходной задачи
обращает первое ограничение
в строгое равенство:
*
(12;20)X =
JJG
12
0,25 0,6 15x x+≤
0,25 12 0,6 20 15
⋅
+⋅=.
Поэтому .
*
1
0y >
Для второго ограничения имеем: 0,25 12 0,2 20 7
⋅
+⋅=. Поэтому .
*
2
0y >
Левая часть третьего ограничения
12
0,5 0, 2 12x x
+
≤ при подстановке
обращается в 1 . Т.к. третье ограничение не стало равенством, то
.
*
(12;20)X = 0
*
3
0y =
Оба утверждения второй теоремы двойственности выполнились. В сле-
дующей лекции будет показана практическая значимость (
*
i
y
1,im= ).
29
Лекция 7. ЭКОНОМИКО-МАТЕМАТИЧЕСКИЙ АНАЛИЗ
РЕШЕНИЯ ЗАДАЧ ЛИНЕЙНОГО ПРОГРАММИРОВАНИЯ
План
1. Анализ дефицитности ресурсов и продукции.
2. Интервалы устойчивости ресурсов.
3. Интервалы устойчивости цен на продукцию.
4. Анализ целесообразности производства.
1. Построение двойственной задачи позволяет провести экономико-
математический анализ (анализ чувствительности) исходной задачи ЛП.
Рассмотрим в качестве исходной задачу оптимального выпуска продук-
ции в матрично-векторной форме:
max
Z
CX
=
⋅→
J
GJJG
,
A
XB
≤
J
JGJG
,
0X ≥
J
JG
.
Здесь
A
– матрица из коэффициентов при неизвестных в сис еме ограничений; т
B
JG
– вектор запасов ресурсов;
C
J
G
– вектор цен продукции; – искомый план
производства продукции, который будет максимизировать доход от реализации
X
JJG
Z
.
Пусть
– решение двойственной задачи ЛП, которое
должно минимизировать расходы на приобретение ресурсов . Введя транспо-
нированную матрицу
12
( , ,..., )
m
Yyy y=
JG
F
T
A
, запишем в матрично-векторной форме двойственную
задачу:
minFBY
=
⋅→
J
GJG
,
T
A
YC≥
J
GJG
,
0Y ≥
J
G
.
Согласно второй теореме двойственности являются
показателем де-
фицитности ресурсов и продукции
. Величину называют двойственной
оценкой
или теневой ценой -го ресурса. Если , то ресурс дефицитный
и при реализации оптимального плана
*
i
y
*
i
y
i
*
0
i
y >
*
X
J
JG
расходуется полностью. Т.е. -е ог-
раничение исходной задачи обратится в строгое равенство. Приобретение до-
полнительной единицы этого ресурса приведёт к увеличению дохода от реали-
зации
i
Z
на величину . Чем больше значение теневой цены, тем дефицитнее
ресурс. Для недефицитного ресурса
*
i
y
*
0
i
y
=
.
В предыдущей лекции был рассмотрен пример 1, в котором тыс.
грн., тыс. грн., тыс. грн. Значит ресурсы , являются де-
фицитными, а ресурс – не дефицитный.
*
1
4,5y =
*
2
11,5y =
*
3
0y =
1
S
2
S
3
S
