Полшков Ю.Н. Курс лекций по экономико-математическому моделированию
Подождите немного. Документ загружается.


30
2. Зададимся следующим вопросом. Как правые части неравенств-ограничений
влияют на оптимальное решение задачи ЛП?
Пусть исходный вектор запасов ресурсов равен
12
(, ,..., )
m
B
bb b=
J
G
. Введём в
рассмотрение приращения и результат таких приращений (
i
bΔ
ii
bb+Δ 1,im= ).
Обозначив через
12
(, ,...,
m
)
B
bb bΔ=Δ Δ Δ
J
G
вектор приращений, получим новый
вектор запасов ресурсов
B
B+Δ
JG JG
. Теперь подставим в исходную и двойствен-
ную задачу вместо
B
J
G
вектор
B
B
+
Δ
JG JG
. Т.о. будет образована симметричная пара
двойственных
многопараметрических задач.
Согласно первой теореме двойственности
max min
Z
F
=
или в другом виде
, где является вектором неизвестных двойственной задачи. Обо-
значим через вектор оптимального решения многопараметрической задачи.
В силу двойственности получим, что
**
CX BY⋅=⋅
JG JJGJGJG
*
Y
JG
*
X
Δ
JJG
**
()CX B BY
Δ
⋅
=+Δ⋅
J
GJJGJGJGGJ
*
.
Рассмотрим приращение целевой функции исходной задачи:
** **
max
()
Z
CX CX B BY BY BY
Δ
Δ=⋅−⋅=+Δ⋅−⋅=Δ⋅
JG JJGJGJJGJGJGJGJGJGJGJG
.
Если изменить только
i -е ограничение, то
*
max
()
iii
Z
by
Δ
=Δ ⋅ . Откуда получим:
*
max
()
i
i
i
Z
y
b
Δ
=
Δ
( 1,im= ).
После предельного перехода имеем:
*
max
i
i
Z
y
b
∂
=
∂
( 1,im= ).
Следовательно, двойственные оценки являются
показателем влияния
ограничений на значение целевой функции
. Поэтому представляет практи-
ческий интерес вычислить предельные значения правых частей системы огра-
ничений (нижней и верхней границы запасов ресурсов), при которых опти-
мальный план останется неизменным.
i
b
*
X
JJG
Зафиксируем базисные неизвестные, вошедшие в оптимальный план.
Пусть данные неизвестные имеют численные значения
*
1
x
,
*
2
x
,…,
*
m
x
. Базис-
ным неизвестным соответствуют векторов-столбцов коэффициентов в мат-
рице, которая получена из матрицы
m
A
добавлением балансовых столбцов при
формировании канонического вида задачи линейного программирования. Со-
ставим из этих векторов-столбцов матрицу
(
)
1, ; 1,
ij
imjm
Ww
==
=
и рассчитаем об-
ратную ей матрицу
(
)
1
1, ; 1,
ij
imjm
Wd
−
==
= .
Двойственные оценки используют для экономического анализа решения
при условии, что запасы ресурсов изменяются лишь в определённых пределах.
Интервалы устойчивости ресурсов находят по формулам
[; ]
iiii
bbbb
−
+
−Δ +Δ
( 1,=im),

31
где
нижний предел уменьшения
i
b
−
Δ
и верхний предел увеличения
i
b
+
Δ
вычисляют следующим образом:
*
0
min
ji
j
i
d
ji
x
b
d
−
>
⎧⎫
⎪⎪
Δ=
⎨⎬
⎪⎪
⎩⎭
,
*
0
min
ji
j
i
d
ji
x
b
d
+
<
⎧
⎫
⎪
⎪
Δ=
⎨
⎬
⎪
⎪
⎩⎭
.
Замечание. Если в -м столбце матрицы i
1
W
−
не окажется отрицательных
чисел, а будут только положительные и равные нулю, то в качестве
i
b
+
Δ при-
нимают . +∞
3. Кроме правых частей ограничений на оптимальный план влияют и значения
коэффициентов целевой функции.
Интервалом устойчивости цены за единицу
j
-й продукции ( 1,
j
n= )
называется отрезок со следующими свойствами. Если цена
, а цены на остальные виды продукции зафиксированы, то оп-
тимальный план выпуска продукции
min max
[;
jj
cc]
]
min max
[;
jj j
cc c∈
*
X
J
JG
останется неизменным.
Чтобы определить интервалы устойчивости, нужно вспомнить геометри-
ческую интерпретацию задач линейного программирования. Опорные планы –
это угловые точки, образованные пересечениями гиперплоскостей из системы
ограничений. При нахождении экстремального значения целевой функции ги-
перплоскость-изоцель с вектором нормали
12
( , ,..., )
n
Ccc c=
J
G
движется к опти-
мальному плану , координаты которого получены в последней симплексной
таблице. На рис. 1 оптимальный план – координаты точки
*
X
JJG
A
.
Рис. 1. Графическая иллюстрация задачи ЛП
32
Однако, если бы коэффициенты целевой функции
12
( , ,..., )
n
Ccc c=
J
G
стали
другими, то изоцель, двигаясь к максимуму, остановилась бы на другой опор-
ной угловой точке. Следовательно, первоначальный оптимальный план изме-
нился бы. Поэтому важно знать интервалы устойчивости коэффициентов целе-
вой функции.
Домашнее задание. Самостоятельно найти интервалы устойчивости ко-
эффициентов целевой функции для примера 1 из лекции 3.
4. Двойственные оценки являются показателем целесообразности производ-
ства новых видов продукции
.
Допустим, имеется возможность начать выпуск продукции . Нормы
расхода ресурсов на производство одной единицы продукции составляют соот-
ветственно ; ;…;
1n
P
+
1, 1n
a
+ 2, 1n
a
+ ,1mn
a
+
. Цена единицы продукции . Целесообраз-
ность производства определяется знаком прибыли от одной единицы продук-
ции:
1n
c
+
*
11 ,1
1
m
nn in
i
ca
++ +
=
Δ= − ⋅
∑
i
y.
Если , то производство прибыльное,
1
0
n+
Δ>
1
0
n+
Δ
= – безубыточное, –
убыточное.
1
0
n+
Δ<
Двойственные оценки также используют как
инструмент сопоставления
условных затрат и результатов
. При изменении количества ресурсов в преде-
лах устойчивости отдельное влияние
i
-го ресурса на величину дохода от реали-
зации определяется, как
*
max
()
iii
Z
byΔ=Δ⋅ 0. Если
max
()
i
Z
Δ
> , то доход увели-
чится на денежных единиц, в противном случае – уменьшится. Сум-
марное влияние изменений количества всех ресурсов вычисляется так:
max
(
i
ZΔ )
*
max max
1
()
m
i
i
ZBY Z
=
Δ=Δ⋅=Δ
∑
J
GJG
.
Рассмотрим возможность дополнительной закупки -го ресурса в объёме
по цене
i
i
b
+
Δ
i
p
за единицу ресурса. Затраты на приобретение составят .
Приращение дохода составит . Если приращение дохода превысит за-
траты на приобретение, т.е.
ii
bp
+
Δ⋅
*
i
by
+
Δ⋅
i
*
0
ii ii
by bp
++
Δ⋅ −Δ⋅>
,
то закупка целесообразна. В противном случае – нет.
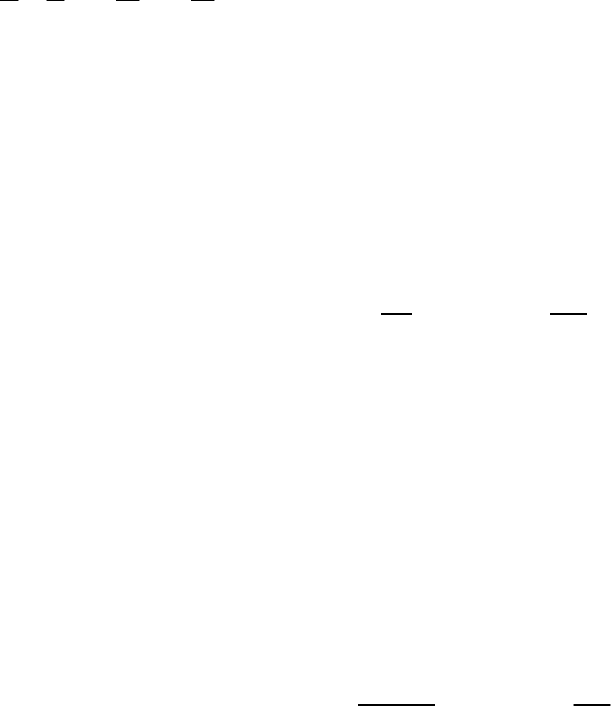
33
Лекция 8. МЕТОД ИСКУССТВЕННОГО БАЗИСА РЕШЕНИЯ
ЗАДАЧ ЛИНЕЙНОЙ ОПТИМИЗАЦИИ
План
1. Метод искусственного базиса.
2. Пример решения задачи ЛП методом искусственного базиса.
1. При решении задач ЛП симплекс-методом предполагалось, что среди векто-
ров
12
, ,..., ,...,
jn
A
AAA имеется единичных векторов. Т.е. в каждом уравне-
нии есть базисная переменная, которая входит лишь в одно уравнение с коэф-
фициентом 1, а в остальные – с коэффициентом 0.
m
Рассмотрим исходную задачу в каноническом виде:
11 2 2
11 1 12 2 1 1
11 2 2
min;
0( 1 ) 0( 1 )
nn
nn
mm mnnm
ji
Zcxcx cx
a x a x ax b,
...................................................,
ax ax ax b,
x j,n, b i,m.
=+ +⋅⋅⋅+ →
+ +⋅⋅⋅+ =
⎧
⎪
⎨
⎪
++⋅⋅⋅+=
⎩
≥= ≥=
(1)
Если
, то соответствующее уравнение умножаем на (–1). 0
i
b <
Составляем расширенную задачу формальным добавлением новых базис-
ных (
искусственных) переменных в уравнения, в которых их нет. В целевую
функцию дописываем их с большим положительным числом
M
. Получим
расширенную задачу:
11 2 2 1 2
11 1 12 2 1 1 1
min;
nn n n nm
nn n
Zcx cx cxМx Мx Мx
a x a x a x x b ,
....................................................................
++ +
+
′
= + + ⋅⋅⋅+ + + +⋅⋅⋅+ →
++⋅⋅⋅++ =
11 2 2
0( 1 ) 0( 1 )
mm mnn nmm
ji
...............................,
a x a x a x x b ,
x j ,n m , b i ,m .
+
⎧
⎪
⎨
⎪
+ +⋅⋅⋅+ + =
⎩
≥=+ ≥=
(2)
Такой подход называют
методом искусственного базиса. Ясно, что ис-
кусственные переменные должны равняться нулю. Если среди них имеются не
равные нулю, то исходная задача (1) несовместная. Или, по-другому, целевая
функция расширенной задачи (2) будет неограниченно расти с ростом
M
и не
сможет достичь минимума. Если в оптимальном плане расширенной задачи ис-
кусственные переменные равны нулю, то остальные переменные дают решение
исходной задачи, если же есть не равные нулю, то исходная задача несовмест-
ная. Если же на некотором этапе, после выведения искусственных переменных
из базиса, возникнет столбец с неположительными членами и положительной
оценкой для данного столбца, то
−
∞→Z. Если в оптимальном плане есть сво-
бодный вектор с нулевой оценкой, то оптимальный план не единственный.
34
2. Рассмотрим решение конкретной задачи ЛП с помощью метода искусствен-
ного базиса.
Пример 2. Решить задачу ЛП:
123
123
12
123
22 ma
21
21
23
0( 13)
j
Zx x x
x x x - ,
x x ,
x x x ,
x j,.
=+ + →
−+ − ≤
⎧
⎪
+≤
⎨
⎪
++=
⎩
≥=
x;
Решение. Переходим к канонической форме. Для этого делаем замену
. В первое и второе ограничения дописываем балансовые переменные ZZ
−=
′
4
x
,
5
x
и первое ограничение умножаем на (–1):
12345
1234
12 5
123
2200 mi
21
21
23
0( 15)
j
Zxxxxx
x x x - x ,
x x x ,
x x x ,
x j , .
′
=−−−++→
−+ =
⎧
⎪
++=
⎨
⎪
++ =
⎩
≥=
n;
В первое и третье уравнение прибавляем, соответственно, искусственные
переменные
6
x
,
7
x
с коэффициентом равным единице. В целевую функцию их
дописываем с коэффициентом
M
. Получили расширенную задачу:
12345 6 7
1234 6
12 5
123 7
2200 mi
2[]1
2[]1
2[]3
0( 1
j
Z xxxxxМxMx
x x x - x x ,
x x x ,
x x x x ,
x j ,
′′
=−−−+++ + →
−+ + =
⎧
⎪
++ =
⎨
⎪
+++ =
⎩
≥=
n;
7).
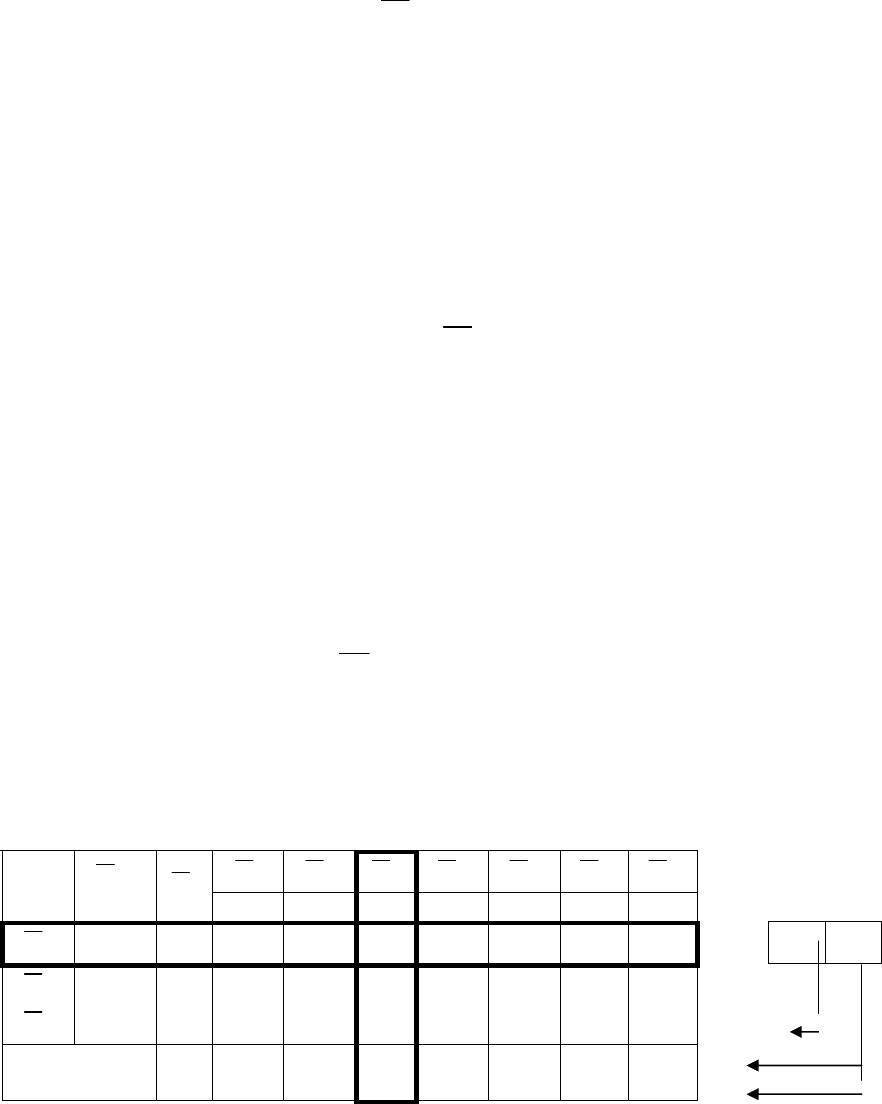
Задачу решаем симплекс-методом (табл. 1).
Табл. 1. Первая симплекс-таблица с комментариями
↓
1
À
2
À
3
À
4
À
5
À
6
À
7
À
θ
1
Б
1
Б
С
1
В
-1 -2 -2 0 0 М М
←
6
À
М 1 1 -2
[1]
-1 0 1 0
[1/1]
-1
-2
5
À
0 1 1 2
0 0 1 0 0
⎯
7
À
М 3 1 2
1 0 0 0 1 3/1
0 1 2 2 0 0 0 0
jj
cz −
4 2 0 2 -1 0 0 0

35
Имеем начальный опорный план
1
(0000113)
Б
X ,,,,,,= при
1
10 20 20 00 01 1 3 0 4 4
Б
Z(X )
М
ММ
′′
=−⋅−⋅−⋅+⋅+⋅+ ⋅+ ⋅=+ =М
.
Числа в индексной строке имеют вид abM
+
и их записывают в виде
. Поэтому индексную строку записывают в двух уровнях. В (1-ю стро-
ку вносят
, а в (2
a
b
⎛⎞
⎜⎟
⎝⎠
)
)
m +
a m
+
-ю строку записывают . Знак числа совпадает
со знаком числа , если 0
b abM+
b b
≠
. Например,
25
25 6 0
6
M
⎛⎞
−
=<
⎜⎟
−
⎝⎠
, ,
, .
0
0
1
⎛⎞
>
⎜⎟
⎝⎠
6
60
1
M
−
⎛⎞
−+ = >
⎜⎟
⎝⎠
0
0
1
⎛⎞
<
⎜⎟
−
⎝⎠
Сначала направляющий столбец выбирают по нижней строке, а после
превращения искусственных переменных в свободные оптимизация произво-
дится по верхней индексной строке.
Покажем, как находится индексная строка:
1
0
()1 103 04
4
Б
ZX МММ
⎛⎞
′′
=⋅ +⋅ +⋅ = + =
⎜⎟
⎝⎠
,
11
1
1101112
2
zc M M M
⎛⎞
−=⋅+⋅+⋅+=+ =
⎜⎟
⎝⎠
,
22
2
2202220
0
zc M M M
⎛⎞
− =−⋅ +⋅+⋅ +=+⋅ =
⎜⎟
⎝⎠
,
33
2
1001222
2
zc M M M
⎛⎞
−=⋅+⋅+⋅+=+ =
⎜⎟
⎝⎠
.
Первый план не оптимален. В нижней индексной строке наибольшую
оценку имеют
1
À
и
3
À
, Выбираем
3
À
, т.к.
21
22
⎛⎞ ⎛⎞
>
⎜⎟ ⎜⎟
⎝⎠ ⎝⎠
.
Этот вектор вводим в базис.
Вычисляем симплексное отношение:
03
13
min 1
11
,
θ
⎧
⎫
=
=
⎨
⎬
⎩⎭
.
Выводим из базиса вектор
6
À
. Составляем табл. 2.
Замечание. После выведения из базиса столбцов, которые отвечают ис-
кусственным переменным, эти столбцы дальше можно не вычислять (они обве-
дены двойной линией). Однако при рассмотрении двойственных задач их обя-
зательно вычисляют.
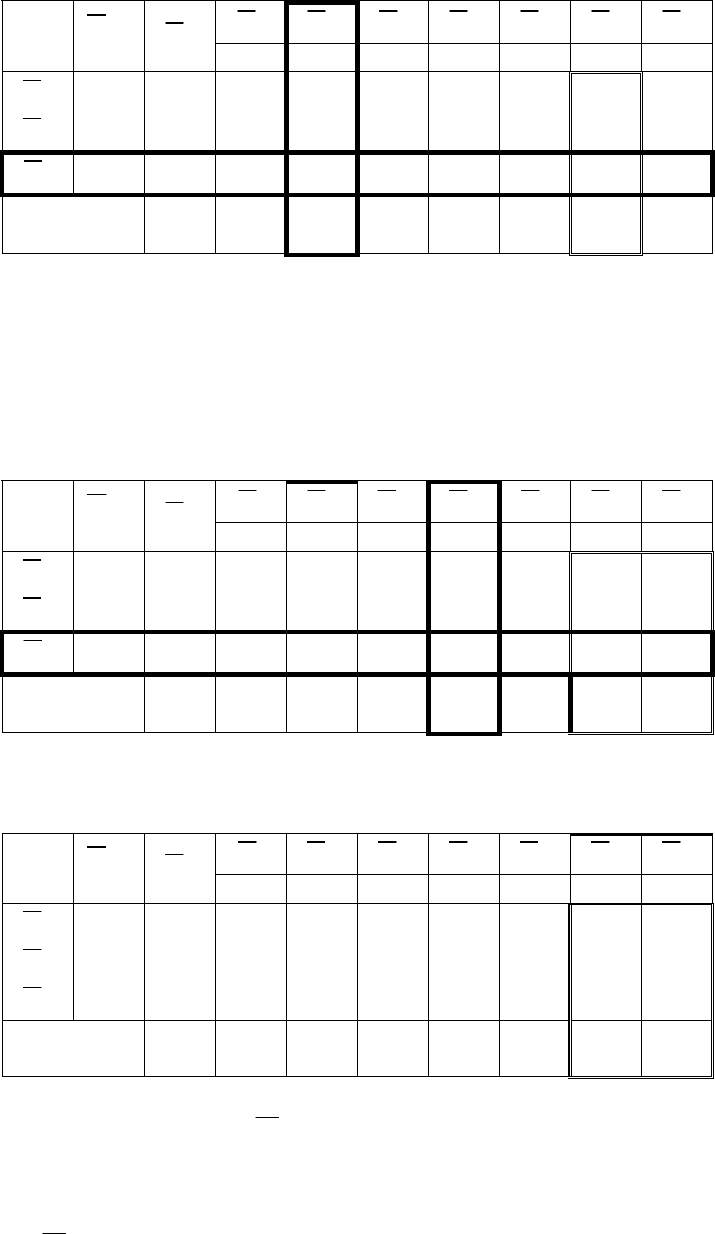
36
Табл. 2. Вторая симплекс-таблица с комментариями
↓
1
А
2
À
3
À
4
À
5
À
6
À
7
À
θ
2
Б
2
Б
С
2
В
-1 -2 -2 0 0 М М
3
À
-2 1 1 -2 1 -1 0 1 0
⎯
5
À
0 1 1 2 0 0 1 0 0 1/2
←
7
À
М 2 0
[4]
0 1 0 -1 1
[1/2]
-2 -1 6 0 2 0 -2 0
jj
cz −
2 0 4 0 1 0 -2 0
Далее совершаем итерации до тех пор, пока не получим отрицательные
оценки в индексной строке. Все вычисления отражены в табл. 3 и табл. 4.
Табл. 3. Третья симплекс-таблица с комментариями
↓
1
À
2
À
3
À
4
À
5
À
6
À
7
À
θ
3
Б
3
Б
С
3
В
-1 -2 -2 0 0 М М
3
À
-2 2 1 0 1 -1/2 0 1/2 1/2
⎯
5
À
0 0 1 0 0 -1/2 1 1/2 -1/2
⎯
←
2
À
-2 1/2 0 1 0
[1/4]
0 -1/4 1/4
[2]
jj
cz −
-5 -1 0 0 1/2 0
-1/2
-1
-3/2
-1
Табл. 4. Четвёртая симплекс-таблица с комментариями
1
À
2
À
3
À
4
À
5
À
6
À
7
À
4
Б
4
Б
С
4
В
-1 -2 -2 0 0 М М
3
À
-2 3 1 2 1 0 0 0 1
5
À
0 1 1 2 0 0 1 0 0
4
À
0 2 0 4 0 1 0 -1 1
jj
cz −
-6 -1 -2 0 0 0
0
-1
-2
-1
Делаем вывод о том, что
(
)
0;0;3;2;1;0;0
opt
X =
,
min
6Z
′
′
=
− . Все искусствен-
ные переменные равны нулю, поэтому начальные переменные определяют оп-
тимальный план.
Ответ:
()
0;0;3Х
∗
=
,
max
6Z
=
.

37
Лекция 9. ТРАНСПОРТНАЯ ЗАДАЧА
План
1. Математическая модель транспортной задачи.
2. Методы построения начального опорного плана транспортной задачи.
1. Рассмотрим следующую задачу ЛП.
Пусть в регионе имеется поставщиков угля (шахт) с запасами ,
,…, . В угле нуждаются потребителей (тепловых электростанций) с по-
требностями , ,…, . Пусть (
m
1
a
2
a
m
a n
1
b
2
b
n
b
ij
c 1,im= , 1,
j
n= ) – цена перевозки единицы
товара (например, за 1 т) от
i -го поставщика
j
-му потребителю.
Требуется определить неизвестные величины
ij
x
( 1,im= , 1,
j
n= ), обо-
значающие объём планируемой перевозки от -го поставщика -му потребите-
лю. Будем стремиться минимизировать общую стоимость перевозок. Задачи та-
кого типа называют
транспортными задачами. Описанная задача однотовар-
ная.
i
j
Если выполняется условие
11
mn
i
ij
a
==
=
j
b
∑
∑
, то совокупные запасы поставщи-
ков совпадают с совокупными потребностями. Тогда это
закрытая транспорт-
ная задача. В противном случае –
открытая (с нарушенным балансом).
Решение открытой задачи сводится к закрытой. Поэтому сформулируем
математическую модель закрытой транспортной задачи.
Пусть
Z
– общая стоимость перевозок. Тогда мы ищем минимум целевой
функции:
11 11 12 12
11
... min
mn
mn mn ij ij
ij
Zcx cx cx cx
==
=+++ = →
∑∑
. (1)
Запишем ограничения задачи:
11 12 1 1
21 22 2 2
12
11 21 1 1
12 22 2 2
12
...
...
................................
...
...
...
................................
...
n
n
mm mn
m
m
nn mnn
m
x
xxa
x
xxa
x
xxa
x
xxb
x
xxb
x
xx
+++=
⎧
⎪
+++=
⎪
⎪
⎪
+++=
⎪
⎨
+++ =
⎪
⎪
+++ =
⎪
⎪
⎪
+++=
⎩
b
(2)
Объёмы перевозок должны быть неотрицательными:
0
ij
x ≥ ( 1,im= ; 1,
j
n= ). (3)
Транспортные задачи удобно записывать табл. 1.

38
Табл. 1. Транспортная таблица
j
b
i
a
1
b
2
b
…
n
b
11
c
12
c
…
1n
c
1
a
11
x
12
x
…
1n
x
21
c
22
c
…
2n
c
2
a
21
x
22
x
…
2n
x
… … … …
…
… … … …
1m
c
2m
c
…
mn
c
m
a
1m
x
2m
x
…
mn
x
Рассмотрим открытую транспортную задачу, у которой суммарные запа-
сы поставщиков больше суммарного спроса потребителей: . Чтобы
сделать задачу закрытой вводят
фиктивного
11
mn
i
ij
a
==
>
∑∑
j
b
)(1n
+
-го потребителя с потребно-
стью и стоимостью перевозок 0. В табл. 1 добавляют столбец
с этой информацией.
1
11
mn
ni
ij
ba
+
==
=−
∑∑
j
b
j
b )
Если же , то вводится фиктивный
11
mn
i
ij
a
==
<
∑∑
(1m
+
-й поставщик с запа-
сом и стоимостью перевозок 0. В табл. 1 добавляется строка.
1
11
nm
mj
ji
ab
+
==
=−
∑∑
i
a
Пример 1. Транспортная задача задана табл. 2.
Табл. 2. Данные задачи
j
b
i
a
15 15 16 18
4 1 2 1
20
4 6 3 2
30
5 2 1 4
10

39
Т.к. , то это открытая транспортная задача. Введём
фиктивного 4-го поставщика с запасом
34
11
60 64
ij
ij
ab
==
=< =
∑∑
4
64 60 4a
=
−= и стоимостью перевозок
0. В табл. 2 добавляем строку и получаем табл. 3.
Табл. 3. Транспортная таблица с фиктивным поставщиком
j
b
i
a
15 15 16 18
4 1 2 1
20
4 6 3 2
30
5 2 1 4
10
0 0 0 0
4
2. Закрытая транспортная задача всегда имеет решение. Поэтому важно уметь
находить начальный опорный план транспортной задачи, который был бы бли-
зок к экстремальному значению целевой функции.
Рассмотрим
метод северо-западного угла. Его суть заключается в том,
что максимально возможная поставка помещается в северо-западную клетку
таблицы. Т.е. максимально возможные поставки заполняют клетки слева напра-
во и построчно.
Пример 2. По данным примера 1 составим начальный опорный план с
помощью метода северо-западного угла (табл. 4).
Табл. 4. Метод северо-западного угла
j
b
i
a
15 15 16 18
4 1 2 1
20
15 5
4 6 3 2
30
10 16 4
5 2 1 4
10
10
0 0 0 0
4
4
