Полшков Ю.Н. Курс лекций по экономико-математическому моделированию

Подождите немного. Документ загружается.

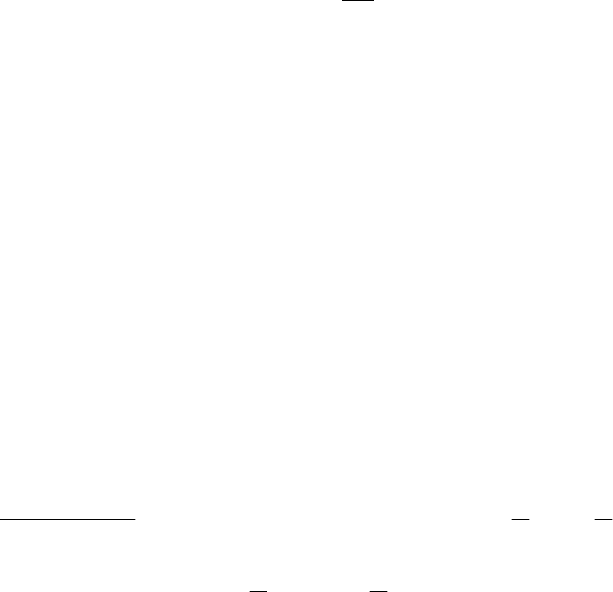
180

∑∑

jij

или

DxV= .

Задача формирования рисковой части оптимального портфеля ставится

следующим образом. При заданной эффективности найти такую структуру

, которая обеспечивала бы минимум функции , т.е. минимальный риск

портфеля. Такая модель была впервые предложена Марковицем в 1951 г.

Мо-

дель Марковица

записывается в следующем виде:

min

pijij

DxxV

=→

∑∑

, (2)

ii p

⎧

⎪

⎨

⎪

⎩

∑

(3)

Иногда налагают условие неотрицательности:

x ≥ ( 1,i= n). (4)

В матричном виде задача (2)-(4) выглядит следующим образом:

min

DxVx=→

, (5)

⎧

⎪

⎨

⎪

⎩

(6)

≥ . (7)

2. Задача (5)-(7) является задачей квадратичного программирования. Задачу (5)-

(6) можно решить методом множителей Лагранжа, а затем учесть условие (7).

Составим функцию Лагранжа:

12 1 2

(, , ) ( 1) ( )

TT T

xxVxIxmx

λλ λ λ

=+ −+ −m.

Это задача на условный экстремум. Согласно необходимому условию экстре-

мума, получим:

(, , )

∂

20Vx I m

+=,

Vx I m

=− −

VI Vm

λλ

−−

=− − .

Ограничения задачи (6) примут линейный вид относительно

mV I mV m m

IV I IV m

λλ

−−

⎧

+=−

⎪

⎨

+=−

⎪

⎩

181

Введя дополнительные обозначения

def

mV I IV m A

−−

= ,

def

mV m B

−

def

VI C

−

= , получим систему:

λλ

+=−

⎧

⎨

+=−

⎩

Решим её методом Крамера:

mA B

−+

Δ−

−

Δ−

Найденные значения множителей Лагранжа подставим в выражение для

оптимальной структуры:

22 22

mA B A mC

VI Vm

ABC ABC

−−

−+ −+

=− ⋅ ⋅ − ⋅ ⋅ =

−−

()( )

VIAmCm IBmA

−

⎡⎤

=−+−+⋅

⎣⎦

−

Для решения задачи (5)-(7) составляют расширенную матрицу:

11 12 1 1

21 22 2 2

22...2 1

... ... ... ... ... ...

22...2 1

... 0 0

11...100

nn nnn

VV Vm

mm m

⎛⎞

⎜⎟

⎝⎠

Её размерность . (2)(2nn+×+)

Оптимальная структура рисковой части фондового портфеля

линейно зависит от и записывается в виде

()

mamb

+ ,

где и – матрицы размерности 1a b n

. Для нахождения их компонент находят

матрицу, обратную матрице

, т.е.

−

⎛⎞

⎜⎟

⎝⎠

…………

………………

…………

………………

Запишем

функцию оптимального риска фондового портфеля

()

pp p p

mcmdm

++,

где , , eb .

caVa= 2

daVb=

Vb=

182

Лекция 8. ПРАКТИЧЕСКИЕ СПОСОБЫ ФОРМИРОВАНИЯ

ОПТИМАЛЬНЫХ ФОНДОВЫХ ПОРТФЕЛЕЙ

План

1. Замечание Тобина к модели Марковица. Комбинированные портфели ценных

бумаг.

2. Практическая реализация модели Марковица-Тобина.

1. Согласно модели Марковица, оптимальная структура

()

mamb

+ (1)

и оптимальный риск портфеля

()

pp p p

mcmdm

++ (2)

зависят от ожидаемой эффективности . Выбор значения зависит от

склонности инвестора к риску. Как разумно определить эту константу?

Один из подходов – использовать

замечание Тобина к модели Маркови-

ца. Джеймс Тобин предложил формировать

комбинированные фондовые

портфели

, т.е. портфели, состоящие из рисковой и безрисковой частей. Рис-

ковая часть представлена «перспективными» акциями, отобранными в порт-

фель. Безрисковая – надёжными облигациями или банковским счётом. Единст-

венной характеристикой последней является

безрисковая эффективность .

Причём, должно выполняться неравенство . В противном случае, в ком-

бинированный портфель не должны включаться рисковые ценные бумаги. На-

личие константы позволяет определить оптимальную ожидаемую эффектив-

ность

рисковой части портфеля. При этом выбор инвестором значения

уже не будет зависеть от его склонности к риску, а будет определяться

макроэкономическим показателем .

mr>

Решение этой задачи имеет графическую интерпретацию. Отложим по

горизонтальной оси показатель , по вертикальной –

. В такой системе ко-

ординат построим кривую риска (2). Отложим на горизонтальной оси точку

и проведём касательную из этой точки к кривой риска. Абсцисса точки касания

определит

оптимальную ожидаемую эффективность *, ордината – опти-

мальный риск

. С помощью (1) будет найдена оптимальная структура

рисковой части фондового портфеля, не зависящая от склонности инвестора к

риску. Полученный таким образом портфель ценных бумаг принято называть

касательным.

Аналитически абсцисса точки касания * определяется из уравнения

касательной к кривой риска:

() (*) (*)( *

pp pp p p p p

mm mmm

σσ σ

−= ⋅−). (3)

183

Касательная проходит через точку . Поэтому подставим в уравнение (3)

. Т.к. данный актив – безрисковый, то

(;0)r

mr=

() 0

. Из уравнения (3) нахо-

дим . *

Замечание 1.

Во-первых, в силу геометрических особенностей, абсцисса

точки касания может оказаться отрицательной или случится так, что

≤

Во-вторых, значение * может оказаться меньшим, чем минимальная ожи-

даемая эффективность рисковой части портфеля, либо большим, чем .

Тогда рекомендуется в качестве * рассматривать

(...

mm m

+++

), т.е.

среднюю арифметическую ожидаемых эффективностей.

Решение задачи Марковица-Тобина подразумевает, что доли вложения

капитала

могут быть любого знака. Если 0, то это означает рекоменда-

цию вложить долю

x ≥

капитала в ценные бумаги вида . Если 0, то это оз-

начает рекомендацию взять в долг ценные бумаги этого вида в количестве

x <

(

)

− , т.е. участвовать в операции «short sale» (игра на ценных бумагах, взятых

в долг). Заметим, что разрешение на «short sale» по конкретной акции даёт

биржа и эта операция далеко не всегда разрешена. На фондовом рынке Украи-

ны она вообще не практикуется.

Замечание 2. Чтобы избегнуть отрицательных долей вложения, можно

задать условие (0

x ≥ 1, n=i ). Это значит, что необходимо найти решение сис-

темы линейных неравенств:

..................

np n

am b

≥

⎧

⎪

≥

⎪

⎨

⎪

≥

⎩

(4)

Если существует решение

, то инвестору предлагается в каче-

стве оптимальной ожидаемой эффективности выбрать середину интервала:

min max

[;

ppp

mmm∈ ]

min max

opt

= .

Замечание 3. Может случиться, что система неравенств (4) не имеет ре-

шения. Практическая рекомендация инвестору может быть следующей. Ценные

бумаги, чьи доли вложения отрицательны, следует исключить из фондового

портфеля («обнулить» доли вложения) и весь капитал инвестора распределить

между оставшимися активами.

2. Продемонстрируем решение задачи Марковица-Тобина на конкретном при-

мере.

184

Пример 1. По данным примера 1 из лекции 12 в портфель ценных бумаг

были отобраны три «перспективные» ценные бумаги, которые характеризуются

столбцом ожидаемых эффективностей и матрицей ковариаций V : m

30,1852

48,4259

65,5556

⎛⎞

⎜⎟

⎝⎠

, .

968,1756 862,9458 24,4856

862,9458 4004,3896 3558,7449

24,4856 3558,7449 10923,457

−

⎛⎞

⎜⎟

−

⎝⎠

Для их расчёта можно использовать функции СРЗНАЧ( ) и КОВАР( ), соответ-

ственно.

Требуется:

1) найти в общем виде структуру оптимального рискового портфеля ()

m и

соответствующий риск ()

и составить портфель с неотрицательными до-

лями вложения;

2) найти оптимальную, не зависящую от склонности инвестора к риску струк-

туру рисковой части портфеля (*, если принять во внимание, что имеются

безрисковые ценные бумаги с эффективностью

)

5%r

. Указать ожидаемую

эффективность * и риск *

полученного портфеля;

3) найти оптимальное распределение вложений (в процентах и денежных сред-

ствах)

, ожидаемую эффективность оптимального комбинированного порт-

феля и его риск

. В портфель инвестируется 4000C

грн., из которых

25% вкладывается в безрисковые ценные бумаги, а оставшиеся 75% – в риско-

вую часть портфеля.

Решение. 1) Составляем расширенную матрицу:

1936,3512 1725,8916 -48,9712 30,1852 1

1725,8916 8008,7791 7117,4897 48,4259 1

Z= -48,9712 7117,4897 21846,914 65,5556 1

30,1852 48,4259 65,5556 0 0

1 1 1 0 0

Оптимальная структура рисковой части портфеля ценных бумаг опреде-

ляется соотношением (1). Для нахождения матриц и найдём матрицу, об-

ратную матрице

a b

4,479E-05 -9,249E-05 4,77E-05 -0,0412 2,3185

-9,249E-05 0,0002 -9,849E-05 0,0267 -0,9603

-1

= 4,77E-05 -9,849E-05 5,079E-05 0,0145 -0,3582

-0,0412 0,0267 0,0145 -15,3651 498,2382

2,3185 -0,9603 -0,3582 498,2382 -17888,943

Вектор-столбцы и b выделены линией. a

Напомним алгоритм действий для вычисления обратной матрицы Z

-1

: а)

выделить место, в котором расположится Z

-1

(в нашей задаче размерность

); б) вызвать функцию МОБР( ) с помощью опции «

» – «Вставка функ-

ции»; в) нажать клавишу «F2» и затем комбинацию клавиш

«Ctrl»+«Shift»+«Enter».

55×

185

Согласно (1) оптимальная структура рисковой части портфеля ценных

бумаг ()

m будет иметь вид:

-0,0412 2,3185

()

m =

0,0267

* +

-0,9603 . (5)

0,0145 -0,3582

Для составления портфеля с неотрицательными долями вложения (см. за-

мечание 2) решим систему (4):

0,0412 2,3185 0

0,0267 0,9603 0

0,0145 0,3582 0

⎧

−+

⎪

≥

−

≥

⎨

⎪

−

≥

⎩

Получим . Оптимальная ожидаемая эффективность: [35,9663;56,2743]

m ∈

35,9663 56,2743

46,1203%

opt

Найдём по формуле (5) структуру оптимального портфеля:

0,4183

x(46,1203) = 0,2711

0,3106

Дисперсия эффективности оптимального портфеля:

()

pp p p

Dm cm dm e

++.

Имеем:

7,6826

caVa== ; ; . 2 498,2382

daVb==− 8944,4715

ebVb==

Использовалась функция умножения матриц МУМНОЖ( ), для которой приме-

ним тот же алгоритм а)-в).

В соответствие с (2) функция оптимального риска фондового портфеля

будет иметь вид:

( ) 7,6826 498,2382 8944,4715

pp p p

mm m

=−+.

Подставляя ожидаемую эффективность , найдём оптимальный

риск портфеля:

46,1203%

opt

m =

(46,1203) 48,0322%

2) На данном этапе нужно найти оптимальную, не зависящую от склонно-

сти инвестора к риску структуру рисковой части портфеля , если при-

нять во внимание, что имеются безрисковые ценные бумаги с эффективностью

. Требуется рассчитать ожидаемую эффективность * и риск *

xm )

5%r =

по-

лученного портфеля.

Из уравнения касательной (3), выводится формула:

dr e

cr d

−

В нашем случае * 36,5384%

186

Согласно (5), находим оптимальную структуру рисковой части фондового

портфеля:

0,8136

x(36,5384) = 0,0141

0,1723

Оптимальный риск портфеля: * (36,5384) 31,5642%

3) Последняя часть задачи предполагает найти оптимальный комбиниро-

ванный портфель ценных бумаг. В портфель инвестируется грн., из

которых 25% вкладывается в безрисковые ценные бумаги, а оставшиеся 75% –

в рисковую часть портфеля. Т.о. доля безрисковой части составляет , а

рисковой – . В денежных средствах это, соответственно, составляет

грн. и грн. Т.е. из 4000 грн. сумма 1000 грн. вклады-

вается в безрисковые ценные бумаги с эффективностью . Оставшиеся

3000 грн. распределяются между тремя рисковыми ценными бумагами. Следо-

вательно, комбинированный портфель состоит из 4-х ценных бумаг. Его струк-

тура

4000C =

0,25x =

10,x−=

1000Cx =

(1 ) 3000Cx−=

5%r =

определяется следующим образом:

(1 )

...

(1 )

⎛⎞

⎜⎟

−

⎜⎟

=−

⎜⎟

−

⎝⎠

Для нашей задачи имеем:

0,2500

0,6102

0,0105

0,1293

Умножив, каждую из долей вложения

на 4000C

грн., найдём распределе-

ние вложений в денежных средствах:

1000 грн.

2440,68 грн.

42,24 грн.

517,08 грн.

Ожидаемая эффективность комбинированного портфеля и его риск

определяются, соответственно, по формулам:

00 0

*(1 )

mrxm x

+⋅−,

*(1 )

⋅− .

Имеем:

5 0,25 36,5384 0,75 28,6538%

m =⋅ + ⋅ = ,

31,5642 0,75 23,6732%

=⋅=

Задание выполнено полностью.

187

Лекция 9. РИСКИ ПРИ КРАТКОСРОЧНОМ СТРАХОВАНИИ ЖИЗНИ

План

1. Таблицы продолжительности жизни.

2. Числовые характеристики индивидуальных исков.

3. Гауссовская модель суммарного иска.

4. Принципы распределения суммарной страховой надбавки.

1. Расчёты, осуществляемые при страховании жизни, имущества и т.п., принято

называть актуарными расчетами, а специалистов по ним – актуариями. Ак-

туарии занимаются расчетом страховых премий и страховых возмещений, оце-

нивают вероятность разорения страховых компаний, работают с данными о

продолжительности жизни населения и т.д.

Статистические данные о продолжительности жизни содержатся в табли-

цах продолжительности жизни (см. приложения). Простейшие таблицы содер-

жат информацию о статистических свойствах времени жизни случайно вы-

бранного человека, у которого известен только его возраст. Такие таблицы на-

зывают общими или упрощенными.

В общих таблицах имеются следующие обозначения:

– возраст;

l – число представителей группы, доживших до

лет;

dll

=− – число представителей группы, умерших в возрасте от

до 1

лет;

– доля (вероятность) представителей группы, доживших до возраста

лет, которые умрут в течение ближайшего года;

L – среднее суммарное число лет, прожитых представителями группы в воз-

расте от

до 1

+ лет;

T – среднее суммарное число лет, прожитых представителями группы в воз-

расте

лет и более;

e – среднее остаточное время жизни.

Например, для некоторой группы из

100000l

человек таблица может иметь

следующий вид (таб. 1):

Табл. 1. Фрагмент общей таблицы продолжительности жизни

0 0,011890 100000 1189 99403,13 7805063,61 78,05

1 0,000982 98811 97 98762,48 7705660,48 77,98

2 0,000709 98714 70 98678,99 7606898,00 77,06

… … … … … … …

32 0,002179 95918 209 95813,42 4673288,63 48,72

33 0,002288 95709 219 95599,42 4577475,21 47,83

… … … … … … …

188

2. Страхование жизни принято называть краткосрочным, если договор заклю-

чается на относительно короткий период (обычно его срок действия не более

года). При краткосрочном страховании в актуарных расчётах не учитываются

такие факты как инфляция и доход от вложения капитала.

Рассмотрим простейшие виды краткосрочного страхования жизни. Кли-

ент платит за страховой полис сумму

грн. Эта сумма называется страховой

премией. Если клиент умрет в течение года, то компания выплатит наследникам

застрахованного страховое возмещение грн. Если же клиент не умрет, то

страховая компания не платит ничего. Величина страховой выплаты , конеч-

но, много больше страховой премии

Возможен и другой вариант краткосрочного страхования жизни, в кото-

ром учитывается причина смерти застрахованного. Т.е., если клиент умрет в

течение года от естественных причин, то компания выплатит наследникам

сумму грн. Если же клиент умрет от несчастного случая, то страховая ком-

пания выплачивает сумму грн. Обычно .

(1)

(2)

(2) (1)

bb>

Итак, купив за

грн. страховой полис, застрахованный пытается ком-

пенсировать наследникам (полностью или частично) риск финансовых потерь,

связанный с неопределённостью момента смерти. Этот риск принят страховой

компанией. Для страховой компании риск, связанный с этим клиентом, заклю-

чается в случайности предъявленного иска. Случайными являются и момент

времени

T прихода индивидуального иска, и его размер

грн.

Пусть возраст застрахованного на момент заключения договора

лет.

Обозначим через – вероятность смерти клиента от естественных причин,

– вероятность смерти от несчастного случая. В сумме эти вероятности со-

ставляют вероятность

(1)

(2)

q , которая содержится в общих таблицах:

(1) ( 2)

qq q=+.

Обозначим через

(0)

−

вероятность не умереть в течение года.

Т.о., размер индивидуального иска

является дискретной случайной ве-

личиной, которая может принимать три значения с тремя соответствующими

вероятностями. Закон распределения индивидуального иска имеет вид:

(1)

(2)

(0)

(1)

(2)

Заметим, что

(0) (1) (2)

1pqq

+=.

Основными числовыми характеристиками индивидуального иска

, как

и любой случайной величины, являются математическое ожидание, дисперсия,

среднее квадратичное отклонение (СКО) и коэффициент вариации.

Математическое ожидание индивидуального иска

, принимающе-

го конечное количество значений

n , рассчитывается по формуле:

189

∑

(1)

Для вычисления дисперсии индивидуального иска

применимы формулы:

() (

iXi ii X

DX x m p x p m

=− = −

∑∑

(2)

Средним квадратическим отклонением, или стандартным отклонением, ин-

дивидуального иска

называют число

= .

(3)

Коэффициентом вариации индивидуального иска

называют число

= .

(4)

Пример 1. Страховая компания заключает договоры страхования жизни

сроком на один год на следующих условиях: если смерть клиента наступила от

несчастного случая, то компания выплачивает наследникам 1000 грн.; в случае

смерти от естественных причин 500 грн.; и не платит ничего, если застрахован-

ный не умер. Возраст застрахованного 35 лет. Вероятность смерти от несчаст-

ного случая 0,0005.

Требуется найти основные числовые характеристики индивидуального

иска

Решение. Из общих таблиц продолжительности (см. приложения) жизни

находим . Из условия задачи . Получаем

0,002540q =

(2)

0,0005q =

(1) (2)

0,002040qqq=− = ,

(0)

1 0,997460pq=− = .

Тогда закон распределения индивидуального иска

имеет вид

0 500 1000

0,99746

0,00204

0,0005

По формулам (1)-(4) найдём основные числовые характеристики:

0 0,99746 500 0,00204 1000 0,0005 1,52

m =⋅ + ⋅ + ⋅ = (грн.),

22 2 2

0 0,99746 500 0, 00204 1000 0,0005 (1, 52) 1007, 69DX =⋅ + ⋅ + ⋅ − = ,

1007, 69 31, 74

== (грн.),

31, 74

20,88

1, 52

c ==.

Пример решён полностью.

Математическое ожидание индивидуального иска в актуарных расче-

тах принято называть нетто-премией. На самом деле плата за страховку долж-

на быть больше нетто-премии, т.к. необходимо покрыть административные

расходы, обеспечить доход, гарантировать малую вероятность разорения ком-

пании. Т.о., страховая премия

должна состоять из нетто-премии и стра-

ховой надбавки :

+ .

(5)