Поклонский Н.А. и др. Полупроводники: основные понятия
Подождите немного. Документ загружается.

31
волновым вектором” k — соотношением k = p
/
ћ; кинетической
энергии частицы K сопо ставляется частота волны ω = K
/
ћ.
# Для электрона, движущегося в посто янном во времени и пери-
одическом в пространстве поле кристаллической решетки, со-
храняется энергия и квазиимпульс p; волновая функция элект-
рона ψ
p
(x + a) = ψ
p
(x)exp(ip
x
a
/
ћ), где a — период решетки, x —
координата. Элек тронные состояния, соответствующие значени-
ям квазиимпульса p
x
и p
x
+ 2πћ
/
a, эквивалентны. Для электрона,
движущегося поперек постоянного в пространстве и перемен-
ного во времени электрического поля плоского конденсатора, со-
храняется импульс и квазиэнергия; волновая функция электро-
на ψ
E
(t + τ) = ψ
E
(t)exp(iE
/
ћω), где ω = 2π
/
τ — круговая частота
поля, t — время. Электронные состояния, соответствующие зна-
чениям квазиэнергии E и E + 2πћω, эквивалентны.
# Квазичастица — эт о делокализованное элементарное в озбуж-
дение конденсированной системы многих частиц. Концепция ква-
зичастиц применима лишь при слабых отклонениях системы от
основного состояния, т. е. когда возбужденное состояние систе-
мы можно представить как газ квазичастиц. Например, концеп-
ция фононов годится до тех пор, пока амплитуда колебаний ато-
мов кристалла мала по сравнению с периодом решетки (т. е. вда-
ли от точки плавления).
# Концепция квазичастиц: вблизи основного состояния энер-
гетический спектр криста лла, состоящего из большого числа
сильно взаимодействующих частиц, “сводится” к спектру слабо
взаимодействующих квазичастиц. Точнее, выделяется подсисте-
ма степеней свободы (частицы), которая ведет себя как газ. Ква-
зичастица не описывает движения отдельной частицы — струк-
турной единицы кристалла. Напротив, как правило, квазичасти-
ца есть форма описания движения всех частиц — такого движе-
ния, которое неразложимо на более простые. Состояния в озбуж-
дения кристалла можно классифицировать следующим образом:
одночастичные — в кристалле есть одна квазичастица, напри-
мер, один фонон; двухчастичные — в кристалле две квазичасти-
цы и т. д. Хотя в рождении (исчезновении) квазичастицы прини-

32
мают участие все атомы кристалла , сама квазичастица — мик-
роскопический объект в том смысле, что ее энергия и (квази)им-
пульс — ат омных масштабов. Так, при низких температ урах сред-
няя энергия акустического фонона порядка тепловой энергии k
B
T,
а экситона — порядка разности энергий в основном и возбуж-
денном состояниях одного атома. Как правило, число квазичас-
тиц, имеющихся в кристалле, огромно даже при низких темпе-
ратурах, хотя при T → 0 их нет вовсе. Так, например, при T = 1
К
в твердом аргоне (диэлектрический кристалл с одним атомом на
примитивную элементарную ячейку и температурой Дебая
T
D
= 92
К) концентрация фононов ≈ 7⋅10
17
см
−3
.
# Угловая частота (волновое число) — скорость изменения
фазы гармонической величины со временем (с расстоянием).
# Групповая скорость — скорость квазичастицы, равная dE
/
dp,
где E — энергия квазичастицы, p — квазиимпульс. Для любого
возбуждения, которое может существовать в кристалле, решетка
представляет собой систему с дисперсией: групповая скорость
возбуждений зависит от квазиволнового вектора (или квазиим-
пульс а). Использование понятия “квазиимпульс ” не обязательно
означает, что чере з кристалл передается “обычный” импульс с
соответствующей скоростью. Так, электрон, для которого груп-
повая скорость dE
/
dp = 0, но p ≠ 0, представляет собой стоячую
волну и обладает нулевым импульсом по отношению к кристал-
лу в целом.
# Фермиевский квазиимпульс p
F
=
F
mE
2
— квазиимпульс
электрона проводимости с кинетической энергией E
F
и эффек-
тивной массой m на поверхности Ферми.
# Закон дисперсии — зависимость энергии квазичастицы (или
частоты волны) от квазиимпульса (или волнового вектора ) — по-
зволяет иллюстрировать изменение как E, так и p в процессах с
участием квазичастицы. Для одноэлектронного возбуждения в
кристалле (даже не обладающем цент ром пространственной ин-
версии) E
↑
(p) = E
↓
(−p), где ст релкой символически указано спи-
новое состояние. Импульсное пространство для описания элек-
тронов удобно тем, что в нем электрон (с определенным значе-
33
нием квазиимпульса p) покоится, хотя в к оординатном, естествен-
но, движется (если dE
/
dp ≠ 0).
# Как и в случае обычных частиц, при столкновениях квазичас-
тиц ∑
i
E
i
= ∑
f
E
f
— суммы энергий всех квазичастиц до и после
столкновения равны. Закон же сохранения квазиимпульса (или
квазиволнового вектора) имеет вид ∑
i
k
i
= ∑
f
k
f
+ b, где в пра-
вой части равенства, помимо суммы всех квазиимпульсов после
столкновения, стоит еще произвольный вектор обратной решет-
ки b. Те процессы, в которых b = 0, называются нормальными
столкновениями, а те, в которых b ≠ 0, столкновениями с пе-
ребросом.
# Первая зона Бриллюэна (ячейка Вигнера –Зейтца обратной
решетки) — область пространства квазиволнового вектора ква-
зичастицы, содержащая все точки, расположенные ближе к дан-
ному узлу обратной решетки, чем к любому другому. Форма зоны
Бриллюэна кристалла определяется только симметрией сопос-
тавляемой ему решетки Браве (например, для алмаза, Si, Ge и
α-Sn первые зоны Бриллюэна имеют форму кубооктаэдра). От
химического со става зависит закон дисперсии квазичастицы и
размер зоны Бриллюэна, где содержится ровно столько разре-
шенных неэквивалентных значений квазиволнового вектора,
сколько примитивных элементарных ячеек содержит трехмер-
ный кристаллический образец.
# Проце ссы переброса — столкновения частиц (квазичастиц) в
кристалле, при которых их суммарный квазиимпульс изменяет-
ся на величину ћb, где b — вектор обратной решетки. Это про-
цессы рассеяния (квази)частиц, когда изменение их квазиимпуль-
са выводит его за пределы первой зоны Бриллюэна. В процессе
переброса квазиимпульс ћb передается кристаллу как целому.
# Особенности Ван Хова — особенности (сингулярности) в за-
висимости плотности состояний квазичастиц в кристалле от их
энергии, связанные с обращением в нуль гр уппов ой скорости ква-
зичастиц в некоторых критических точках зоны Бриллюэна.
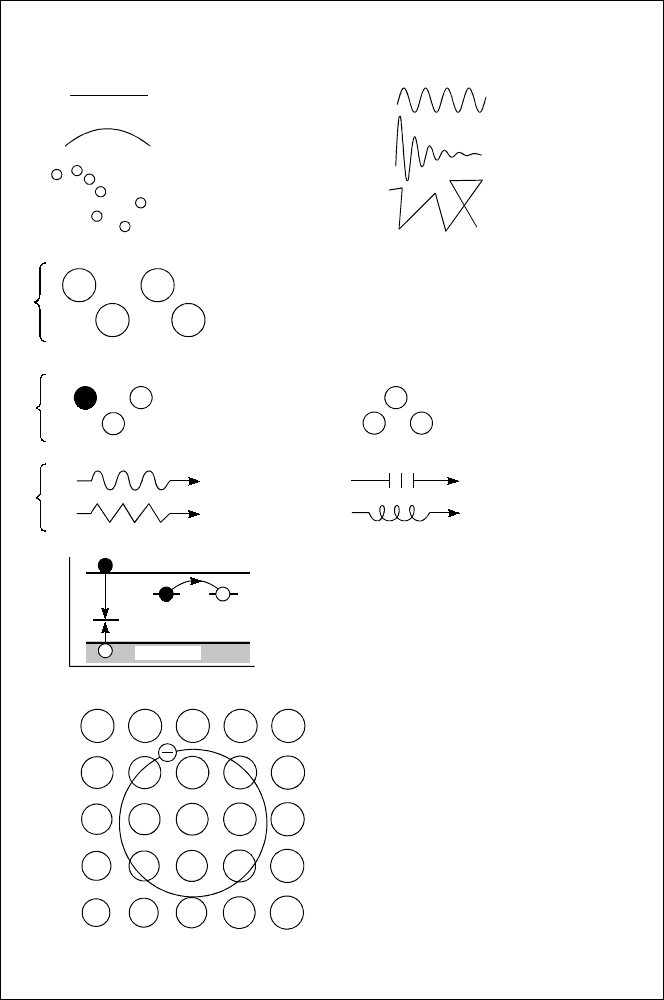
34
+2
−3
−1
e
−
+
h
+1
Натяжение,
равномерность
“Замороженный”
беспорядок
Податливость
Периодичность,
спокойствие
Диссипация
энергии
Броуновское
движение
а) б)
в)
г)
д)
е)
ж)
Атомы, атомные остовы, точечные дефекты
кристаллической решетки, обладающие
зарядом +2, 0, −3, −1 (в единицах модуля
заряда электрона)
Электроны
проводимости
Дырки (электронные
вакансии)
ПлазмонФотон
Фонон Магнон
Энергия
Координата
c-зона
v-зона
а), …, ж) Графика статики и динамики. Условные обозначения ато-
мов, ионов и некоторых элементарных возбуждений в кристалле.
Эксит он в кристалле из “нейтраль-
ных” атомов (электрон одного ато-
ма возбужден светом на водородо-
подобную орбиту вокруг элект-
ронной вакансии (дырки)) может
мигрировать по узлам решетки,
перенося энергию возбуждения,
но не заряд
Рекомбинация электрона и дырки на ло-
вушк е. Прыжковый переход электрона
между локализованными состояниями в
запрещенной зоне
# Представление состояний и процессов в кристалле

35
а), б) Зависимости полной энергии электрона — (
•
) (позитро-
на —
!
) (E
/
c)
2
= (m
0
c)
2
+ (hk)
2
и фотона E (эВ) ≈ 0.197⋅k (мкм
−1
) в
вакууме от их волновых векторов k, k; кинетическая энергия элек-
трона K ∝ k
2
/
m
0
; минимальная энергия, необходимая для рождения
электронно-позитронной пары E
g
= 2m
0
c
2
≈ 1.02 МэВ.
в) Зависимость полной энергии E электрона в c-зоне (дырки в
v-зоне) кристаллического кремния от квазиволнового вектора k в
направлении [100]; зависимость E от k повторяется с периодом
4π
/
a, где а ≈ 0.543 нм — период решетки; 1, 1' — прямые (верти-
кальные) переходы электронов из v- в c-зону при поглощении фо-
тонов; 2 — оптический переход с испусканием (поглощением) фо-
нона с волновым вектором q ≈ k
b
и энергией ћω
q
; 3, 3' — термализа-
ция электрона, дырки; h, l — подзоны тяжелых и легких дырок;
k
b
≈ ± 10 нм
−1
; E
g
≈ 1.1 эВ. Кинетическая энергия электрона с эф-
фективной массой m в одной долине с-зоны: K = h
2
(k − k
b
)
2
/
2m.
г) Зависимость энергии ћω
q
фононов от их квазиволнового век-
тора q в Si в направлении [100] (LA — продольные акустические
фононы, ТО — поперечные оптические); зависимость ω
q
от q по-
вторяется с периодом 4π
/
a.
# Законы дисперсии для частиц и квазичастиц
k
E
g
K
=
(ћk)
2
2m
0
E
E
=
cћk
0
k
E
k
b
l
h
0
2π
a
-
2π
a
k
E
g
E
3'
1'
1
2
3
ћω
q
50 мэВ
02π
/
a
2TO
LO
LA
2TA
q
а) б)
в) г)
36
3. КОЛЕБАНИЯ КРИСТАЛЛИЧЕСКОЙ РЕШЕТКИ
# Колебания кристаллической решетки — согласованные сме-
щения составляющих кристалл атомов около положений равно-
весия (узлов решетки). Амплитуда колебаний тем больше, чем
выше температура кристалла. На тепловые колебания кристал-
лической решетки могут налагаться колебания, вызванные рас-
про ст ранением в кристалле упругих волн, порождаемых вне-
шним воздействием. При упругом характере межатомного взаи-
модействия колебательная энергия кристалла равна сумме энер-
гий так называемых нормальных колебаний, каждое из которых
вовлекает в движение все атомы. Каждый атом в данном нор-
мальном колебании движется около положения равновесия; тра-
ектории движения одинаковы для эквивалентных по расположе-
нию в решетке и
/
или сорту атомов. В т рехмерном крист алле,
состоящем из N примитивных элементарных ячеек по β атомов в
каждой, существуют 3βN − 6 нормальных колебаний, которые
группируются в 3β ветвей: 3 акустических и 3(β − 1) оптичес-
ких. Нормальное колебание можно представить в виде двух уп-
ругих плоских волн, распространяющихся в противоположных
направлениях. Для длин волн много больших межатомного рас-
стояния, акустическим колебаниям решетки соответствуют
смещения элементарной ячейки как целого, а оптическим —
смещения атомов внутри примитивной элементарной ячейки.
Энергию колебательного состояния кристалла можно рассмат-
ривать и как сумму энергий фононов — квантов энергии упру-
гих колебаний. Квантов ая природа колебаний кристаллической
решетки проявляется в наличии нулевых колебаний ат омов при
абсолютно м нуле температур ы.
# В гармоническом приближении кинетическая энергия движе-
ния сов окупности атомов решетки есть сумма кинетических энер-
гий отдельных атомов, причем каждое слагаемое суммы зависит
от одной точки пространства. Потенциальная же энергия содер-
жит как члены, пропорциональные квадратам смещений отдель-
ных атомов, так и перекрестные члены, пропорциональные про-
изведению смещений пары атомов в разных точках криста лла.
37
Если с уществ ует систем а координат, в кот орой перекрестные чле-
ны исчезают, то координаты называются “нормальными коор-
динатами”. Тогда колебательная энергия кристалла будет равна
полной энергии совокупно сти невзаимодействующих объек-
тов — нормальных мод колебаний. Если нормальную моду ко-
лебания кристалла сопоставить с квантом энергии и, следова-
тельно, с квазичастицей (так называемым фононом), то ей мож-
но приписать квазиимпульс (импульс ?) ћq. Тогда мы можем рас-
сматривать энергию колебательных состояний решетки как на-
бор квазичастиц — фононов. Однако импульс фонона отличает-
ся от импульса частицы тем, что не может возрастать неограни-
ченно. Он может изменяться каждый раз на величину, кратную
ћb (где b — вектор обратной решетки); этот импульс “передает-
ся” решетке как целому, потому что фонон может существовать
только в решетке . Конечно, сумма всех импульсов, переданных
решетке, равна нулю и кристалл как целое не получает импульса
от собственных волн решетки. И все же при рождении или унич-
тожении фононов внешними возбуждениями (например, при не-
упругом рассеянии тепловых нейтронов) обычный импульс пе-
редается кристаллу. Энергия нормальной моды колебания (и фо-
нона) распределена по кристаллу в реальном пространстве, но
локализована в пространстве q для каждого из j типов колеба-
ний, где j = 3β — число степеней свободы примитивной элемен-
тарной ячейки, β — число атомов на ячейку. Моды колебаний,
вызывающие смещение центра массы примитивной ячейки, на-
зываются акустическими; моды, которые затрагивают только
внутренние степени свободы ячейки, называются оптическими.
Различие между этими модами колебаний наибольшее при
|q| << |b| (длинные волны). Число мод колебаний равно 3βN − 6,
где N — число примитивных ячеек в образце. Спектр собствен-
ных част от к олебаний кристалла ω(q) состоит из чередующих-
ся разрешенных и запрещенных зон. Число разрешенных зон
(“ветвей” колебаний) равно 3β; число различных квазиволновых
векторов q в зоне равно N − (2
/
β) ≈ N, так что общее число час-
тот (мод колебаний) равно числу колебательных степеней сво-
боды 3βN − 6 ≈ 3βN. Различимые значения q ограничены 1-й
38
зоной Бриллюэна. Число акустических фононов N
p
∝ (T
/
T
D
)
3
при T << T
D
и N
p
∝ T
/
T
D
при T > T
D
, где T
D
— температура Дебая.
Число оптических фононов N
po
∝ exp(−ћω
o
/
k
B
T) при k
B
T << ћω
o
,
где ω
o
— средняя частота оптических фононов в кристалле, и
N
po
≈ 3(β − 1)Nk
B
T
/
ћω
o
при k
B
T >> ћω
o
.
# Фонон — квазичастица, описывающая коллективные колеба-
ния атомов в кристалле при T > 0. Энергия колебательного дви-
жения решетки (кристалла) приближенно равна сумме энергий
фононов. Фононный газ — это бозе-газ с равным нулю хими-
ческим потенциалом.
# Закон Гука: в зоне упругости материала деформации пропор-
циональны напряжениям (давлениям).
# В аморфном твердом теле фононы с малыми квазиимпульса-
ми ввести можно, а с большими нельзя. Возможность введения
фононов с малыми импульсами связана с тем, что при колебани-
ях с большой длиной волны а т омная структура тела несуществен-
на: твердое тело воспринимается как упругий континуум. Когда
же длина волны фонона сопоставима с расстоянием между со-
седними атомами, расположение атомов в пространстве суще-
ственно для распространения фонона (возбуждения).
# Локальные колебания — ко ллек тивные колебания ато мов, рас-
положенных в окрестности необладающего внутренними коле-
бательными степенями свободы де фекта (примеси) кристалли-
ческой решетки; частоты локальных (щелевых) колебаний попа-
дают в одну из запрещенных зон (щелей) спект р а частот идеаль-
ног о кристалла. Колеба тельный спектр окрестности примеси (де-
фекта решетки) как бы настроен в резонанс с локальной часто-
той и выведена из резонанса с кристаллическими частотами. Для
релаксации локальных колебаний требуется ангармонический
процесс, в котором квант энергии локальных колебаний может
распасться на два или более фононов . Частоты так называемых
квазилокальных колебаний примеси попадают в одну из раз-
решенных зон (ветвей) частот и оказываются в резонансе с соб-
ственными частотами крист алла — матрицы. Квазилокальное
колебание нестационарно уже в приближении гармонических
39
колебаний атомов и, раз возникнув, оно распадается самопроиз-
вольно, возбуждая колебания всего кристалла. Относительное
(приведенное к одинаковой частоте колебаний) время жизни ква-
зилокального колебания меньше времени жизни локального ко-
лебания. Аналогично классифицируют (на локальные и квази-
локальные) внутримолекулярные колебания примесной молеку-
лы, состоящей из нескольких атомов примеси в решетке.
# Описание вибронного взаимодействия — взаимодействия
электронного движения с колебательным движением ядер (ион-
ных остовов) в молекуле (дефекте решетки) — лежит за преде-
лами адиабатического приближения.
# Низкочастотная динамика, как правило, присуща системам,
а высокочастотная — подсистемам (ср. акустические и опти-
ческие колебания кристаллической решетки).
# Акустические колебания кристаллической решетки — ко-
лебания, частота ω
a
которых пропорциональна волновому век-
тору q (для q << b, где b — вект ор обратной решетки). Прими-
тивная элементарная ячейка участвует в акустических коле-
баниях как целое. Число “ветвей” колебаний, т. е. зависимостей
ω
a
(q), равно трем (2TA + LA).
# Отношение импульсов акустического фонона и равного ему
по энергии фотона равно отношению скоростей света c и звука
v
a
в кристалле. В силу того, что v
a
<< c, одновременное выполне-
ние законов сохранения энергии и импульса в процессе превра-
щения одного фотона в один поперечный акустический (или оп-
тический) фонон без участия так называемого “третьего тела”
невозможно; в первом приближении поперечные электромаг-
нитные волны не взаимодействуют с продольными колеба-
ниями кристаллической решетки.
# Оптические колебания кристаллической решетки связаны
с относительным смещением атомов в примитивной элементар-
ной ячейке с числом атомов β ≥ 2, т. е. возмо жны лишь в решет-
ках с базисом, когда с каждым узлом сопост авляемой кристаллу
решетки Браве связано два и более неэквивалентных по распо-
ложению и
/
или сорту атомов. Число оптических “ветвей” ω
o
(q)
40
равно 3(β − 1); частота оптических колебаний ω
o
слабо (по срав-
нению с акустиче скими колебаниями) зависит от волнового век-
тора q. Энергия практиче ски любого оптического фонона ћω
o
в
кристаллическом кремнии примерно равна 60 мэВ, в GaAs —
30 мэВ.
# Температура Дебая T
D
определяется предельными частотами
акустических колебаний ω
D
, разграничивающих область низких
и высоких температур по отношению к решеточным свойствам
кристалла. При температуре T > T
D
теплоемкость решетки (в гар-
моническом приближении C
P
= C
V
) не зависит от T, а при T < T
D
она пропорциональна T
3
. В модели Дебая величина ћω
D
= k
B
T
D
представляет собой максимальный квант энергии колебаний ре-
шетки. Для крист алла, со стоящего из атомов одного сорта,
ћω
D
= ћ[18π
2
/
((2v
t
−3
+ v
l
−3
)V
1
)]
1/3
, где v
t
, v
l
— скорости попереч-
ных и продольных акустических (звуковых) волн, V
1
— объем,
приходящийся на атом. Для алмаза T
D
≈ 2230 К, для Si — 645 К,
для Ge — 374 К. Температурой Дебая для оптических колебаний
решетки называют величину ћω
—
o
/
k
B
, где ω
—
o
— средняя частота
оптических фононов.
# При упругом рассеянии (брэгговской дифракции) рентгено-
вских фотонов (квантов, лучей) на кристалле справедливо пра-
вило отбора для волновых векторов: k' = k + b, где k и k' —
волновые векторы падающего и рассеянного фотонов, b — век-
тор обратной решетки; при брэгговском рассеянии фотона крис-
талл в целом будет испытывать отда чу с импульсом ћb. Если фо-
тон испытывает неупругое рассеяние, при котором образуется
фонон с волновым вектором q, то k' + q = k + b. Если же при
неупр угом рассеянии фотона поглощается фонон с во лновым век-
тором q, то k' = k + q + b. Процесс переброса импульса фотона в
кристаллической решетке можно представить как ро ждение (или
уничтожение) им фонона с одновременным брэгговским отра-
жением. Опыты по неупругой дифракции пучка частиц на крис-
талле практически осуществляют с “тепловыми” нейтронами,
длина волны которых порядка постоянной решетки a = 2π
/
b, а
энергия порядка 0.1 эВ. При этом изменение энергии нейтрона
