Питолин В.М., Попова Т.В., Беляков П.Ю., Кобзистый С.Ю. Теоретические основы электротехники: элементы теории с примерами решения задач. Учебное пособие
Подождите немного. Документ загружается.


40
совпадают;
B90EE
333
== – алгебраическая сумма ЭДС третьего
контура.
Система уравнений для определения контурных токов в
матричной форме записи имеет вид:
−
=
⋅
−
−−
−
90
100
180
I
I
I
90500
5021590
090150
33
22
11
.
Контурные токи определяются по формуле:
∆
∆
=
k
kk
I
.
Главный определитель системы:
6
10798,1
90500
5021590
090150
⋅=
−
−−
−
=∆
.
Дополнительные определители получаем путем замены
k-го столбца главного определителя на столбец свободных
членов:
6
1
10818,1
905090
50215100
090180
⋅−=
−
−
−−
=∆
;
6
2
1067,5
90900
5010090
0180150
⋅=
−−
−
=∆
;
6
3
10114,2
90500
10021590
18090150
⋅=
−
−
−−
=∆
.
Рассчитаем контурные токи:

41
,A011,1
10798,1
10818,1
I
6
6
1
11
−=
⋅
⋅−
=
∆
∆
=
,A315,0
10798,1
1067,5
I
6
6
2
22
=
⋅
⋅
=
∆
∆
=
.A175,1
10798,1
10114,2
I
6
6
3
33
=
⋅
⋅
=
∆
∆
=
Токи в ветвях цепи будут определяться наложением кон-
турных токов. Причем контурные токи, направления которых
совпадает с выбранным ранее положительным направлением
тока ветви, берутся со знаком «плюс», а те, которые не совпа-
дают, со знаком «минус»:
,A315,0II
221
=
=
,A011,1II
112
=−=
,A175,1II
333
=
=
,A326,1011,1315,0III
11224
=
+
=
−
=
.A895,0175,1315,0III
33225
−
=
−
=
−
=
1.2.7 Рассчитать токи в ветвях электрической цепи, схема
которой представлена на рис. 1.23 методом узловых потенциа-
лов, используя данные задачи
1.2.5.
При расчете электрических цепей методом узловых по-
тенциалов, неизвестной величиной являются потенциалы узлов
рассматриваемой цепи, при условии, что потенциал одного из
узлов цепи принимают равным нулю.
Рассматриваемая цепь имеет три узла, примем равным
нулю потенциал третьего узла φ
3
= 0, тогда необходимо будет
составить систему из двух уравнений для определения потен-
циалов остальных узлов. В общем виде эта система имеет вид:
=ϕ+ϕ
=ϕ+ϕ
,JGG
;JGG
22222121
11212111
где G
kk
– узловая проводимость k-того узла, которая определя-
ется как сумма проводимостей ветвей, подходящих к соответ-

42
ствующему узлу:
;Cм041,0
90
1
60
1
75
1
R
1
R
1
R
1
G
421
11
=++=++=
;Cм058,0
50
1
40
1
75
1
R
1
R
1
R
1
G
531
22
=++=++=
См013,0
75
1
R
1
GG
1
2112
−=−=−== – междуузловая
проводимость, определяемая как сумма проводимостей ветвей,
включенных непосредственно между первым и вторым узлами,
которая в методе узловых потенциалов всегда берется со зна-
ком «минус»;
∑
=
kkkk
EgJ – алгебраическая сумма условных узловых
токов, создаваемых ЭДС ветвей, подходящих к k-тому узлу, в
том случае если ЭДС направлена к узлу, то создаваемый ею
узловой ток входит в сумму с положительным знаком, если же
от узла, то с отрицательным:
;A333,4
60
180
75
100
R
E
R
E
J
2
2
1
1
11
=+=+=
.A917,0
40
90
75
100
R
E
R
E
J
3
3
1
1
22
=+−=+−=
Запишем полученную систему уравнений для определе-
ния потенциалов узлов в матричной форме:
=
ϕ
ϕ
⋅
−
−
917,0
333,4
058,0013,0
013,0041,0
2
1
.
Определим главной и дополнительные определители этой
системы уравнений:
;10209,2
058,0013,0
013,0041,0
3−
⋅=
−
−
=∆

43
;263,0
058,0917,0
013,0333,4
1
=
−
=∆ .094,0
917,0013,0
333,4041,0
2
=
−
=∆
Определим неизвестные потенциалы узлов:
;B058,119
10209,2
263,0
3
1
1
=
⋅
=
∆
∆
=ϕ
−
.B533,42
10209,2
094,0
3
2
2
=
⋅
=
∆
∆
=ϕ
−
Токи в ветвях схемы найдем по закону Ома для участка
цепи с ЭДС:
∑∑
±
ϕ
−
ϕ
=
±
=
R
E)(
R
EU
I
baab
,
где U
ab
= (φ
a
– φ
b
) – напряжение на зажимах всего участка це-
пи, и направление этого напряжения должно совпадать с на-
правлением искомого тока; Е – ЭДС участка цепи, которая бе-
рется со знаком «+», если ее направление совпадает с направ-
лением искомого тока или со знаком «–», если не совпадает;
∑
R – сумма сопротивлений данного участка цепи.
;A315,0
75
100)058,119533,42(
R
E)(
I
1
112
1
=
+
−
=
+ϕ
−
ϕ
=
;A016,1
60
180)058,1190(
R
E)(
I
2
213
2
=
+
−
=
+ϕ
−
ϕ
=
;A187,1
40
90)533,420(
R
E)(
I
3
323
3
=
+
−
=
+ϕ
−
ϕ
=
;A323,1
90
058,119
R
)(
I
4
31
4
==
ϕ
−
ϕ
=
.A851,0
50
)533,420(
R
)(
I
5
23
5
−=
−
=
ϕ
−
ϕ
=
Если сравнить между собой методы определения токов в
рассматриваемой цепи (рис. 1.23), то наиболее целесообразным
окажется метод узловых потенциалов, так как для расчета то-
44
ков этим методом необходимо решить систему уравнений все-
го лишь второго порядка. Расхождения в результатах расчета
токов в одной схеме различными методами объясняется по-
грешностями, возникающими в результате округлений.
1.2.8 Рассчитать мощности приемников и источников
электрической энергии и проверить выполнение баланса мощ-
ностей для электрической цепи, приведенной в задаче
1.2.6.
Уравнение баланса мощностей записывается следующим
образом:
,IRIE
n
1K
2
KKK
l
1K
K
∑∑
==
=
где
K
l
1K
K
IE
∑
=
– мощность, генерируемая источниками ЭДС;
∑
=
n
1K
2
KK
IR – мощность, рассеиваемая в резисторах.
Рассчитаем суммарную мощность источников ЭДС. На-
правления токов в ветвях, содержащих источники энергии и
направления ЭДС совпадают, то есть все источники работают в
режимах генератора, и поэтому их мощность будет входить в
сумму со знаком «+»:
.Вт23,319175,190011,1180315,0100
IEIEIEР
3322!1ИСТ
=⋅+⋅+⋅=
=++=
∑
Рассчитаем суммарную мощность приемников, которая
всегда имеет положительное значение и определяется как сум-
ма мощностей всех приемников:
.Вт133,319
859,050326,190175,140011,160315,075
IRIRIRIRIRP
22222
2
55
2
44
2
33
2
22
2
11ПР
=
=⋅+⋅+⋅+⋅+⋅=
=++++=
∑
Из выполненных расчетов видно, что суммарная мощность ис-
точников энергии равна суммарной мощности приемников
электрической энергии, незначительное расхождение в значе-
ниях возникает из-за округлений при расчете токов цепи.
45
2 ЛИНЕЙНЫЕ ЦЕПИ СИНУСОИДАЛЬНОГО ТОКА
2.1 Основы теории
2.1.1 Синусоидальный ток и его параметры
Синусоидальными токами и напряжениями называются
токи и напряжения, которые изменяются во времени по сину-
соидальному закону.
Мгновенные значения синусоидальных тока и напряже-
ния определяются выражениями:
i(t) = I
m
sin(ωt + ψ
i
), u(t) = U
m
sin(ωt + ψ
u
),
где I
m
, U
m
– амплитудные значения тока и напряжения;
(ωt + ψ) – фаза колебания, аргумент синусоидальной функ-
ции;
ω [рад/с] – угловая частота, которая может быть определена
как: ω = 2πf = 2π/T;
f, Гц – линейная частота; Т, c – период колебаний;
ψ
i
, ψ
u
- начальные фазы тока и напряжения, которые отсчи-
тываются от начала координат до ближайшей точки на оси
абсцисс перехода синусоидальной функции через ноль от от-
рицательных к положительным ее значениям. Начальная фаза
может быть положительной, отрицательной и равной нулю.
При ψ>0 начало синусоиды сдвинуто влево относительно на-
чала координат, при ψ < 0 – вправо, а при ψ = 0 синусоида про-
ходит через начало координат.
На рис. 2.1 построены временные графики мгновенных
значений тока и напряжения одинаковой частоты:
i(t)= I
m
sin(ωt + ψ
i
), u(t)= U
m
sin(ωt + ψ
u
).
Угол, на который синусоида тока сдвинута относительно
синусоиды напряжения, называют
углом сдвига фаз φ и его оп-
ределяют как разность начальных фаз напряжения и тока:
φ = ψ
u
– ψ
i
.
Если угол φ>0, то говорят, что ток отстает по фазе от
напряжения; если угол φ <0, то говорят, что ток опережает
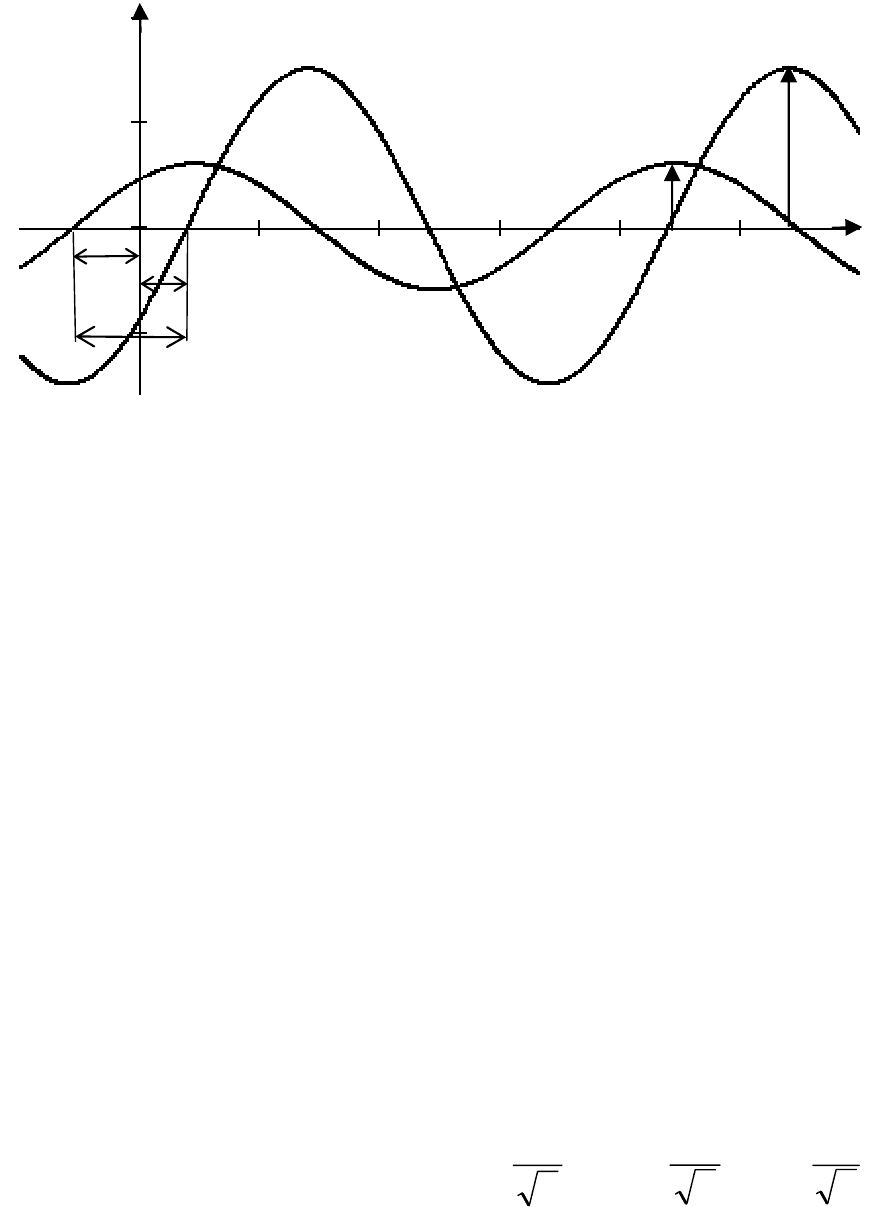
46
напряжение по фазе; при значении угла φ = 0, говорят что ток
совпадает по фазе с напряжением.
Рис. 2.1
2.1.2 Действующие и средние значения периодических
ЭДС, напряжений и токов
О величине периодических ЭДС, напряжений и токов
обычно судят по их средним квадратичным значениям за пери-
од, которые называются
действующими значениями ЭДС, на-
пряжения или тока и обозначаются, соответственно, как E, U, I.
Под действующим значением синусоидального тока i по-
нимают такой постоянный ток I, который при протекании че-
рез сопротивление R выделяет такое же количество тепла, что
и синусоидальный ток за время, равное одному периоду сину-
соидального тока.
Большинство систем измерительных приборов измеряют
действующие значения токов и напряжений. Поэтому расчеты
в цепях синусоидального тока чаще всего выполняются по
действующим значениям, которые связаны с амплитудными
следующими соотношениями:
2
E
E
m
= ,
2
U
U
m
= ,
2
I
I
m
= .
Среднее арифметическое значение синусоидальных ЭДС,
φ
ψ
u
ψ
i
i,u
i
(
t
)
u
(
t
)
I
m
U
m
ωt
47
напряжений и токов равно нулю. Поэтому вводят понятие об
их
среднем значении за положительный полупериод, которое
определяется как:
π
=
m
cp
U2
U ,
π
=
m
cp
I2
I.
2.1.3 Изображение синусоидальных величин
векторами и комплексными числами
Синусоидальные ЭДС, напряжения и токи, имеющие час-
тоту ω, можно изображать векторами на плоскости декартовых
координат, вращающимися с угловой скоростью, равной ω,
причем длина вектора определяется в соответствующем мас-
штабе амплитудой ЭДС, напряжения или тока.
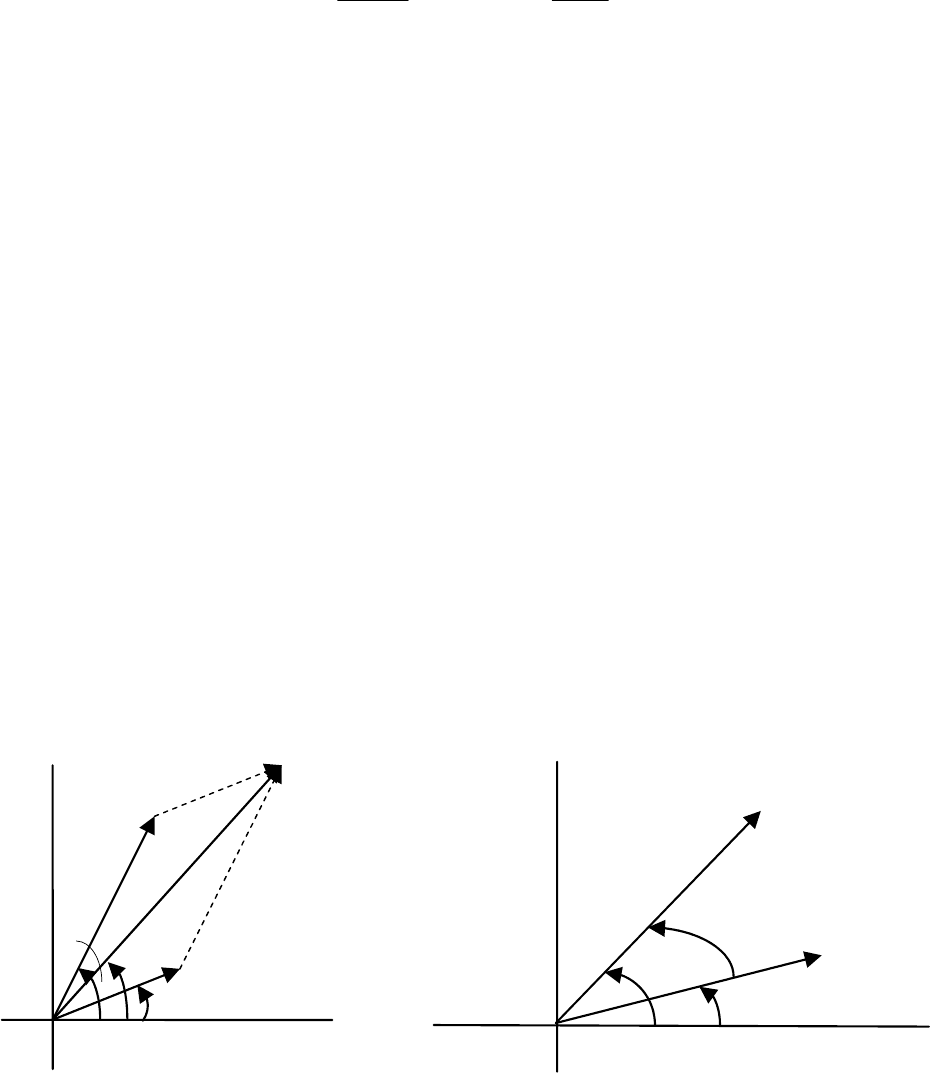
Пусть мы имеем две синусоидальные ЭДС:
)tsin(Ee
1m11
ψ
+
ω= и )tsin(Ee
2m22
ψ+
ω
=
.
Изобразим их в виде векторов в момент времени равный
нулю (рис. 2.2). Начальные фазы этих синусоидальных ЭДС
откладываются от горизонтальной оси против часовой стрелки,
если они положительны, и по часовой стрелке, если они отри-
цательны. Длины векторов равны соответствующим амплитуд-
ным значениям.
Найдем ЭДС е, равную сумме ЭДС е
1
и е
2
. Тогда эта ЭДС
E
r
1m
E
r
2m
E
r
m
ψ
1
ψ
ψ
2
Рис. 2.2
I
r
U
r
ψ
i
ψ
u
φ>0
Рис. 2.3
48
е будет изображаться вращающимся вектором, равным геомет-
рической сумме векторов, изображающих ЭДС е
1
и е
2
.
В любой момент времени взаимное расположение этих
вращающихся векторов будет оставаться неизменным, поэтому
достаточно построить векторы в момент времени равный ну-
лю, и все операции выполнять над ними.
Совокупность векторов, характеризующих процессы,
происходящие в той или иной цепи синусоидального тока, и
построенных с соблюдением правильной ориентации их друг
относительно друга для момента времени равного нулю, назы-
вают
векторной диаграммой.
Так как обычно мы интересуемся действующими значе-
ниями синусоидальных функций, которые в
2 раз меньше их
амплитуд, то целесообразно на векторной диаграмме длину
векторов выбирать равной, в избранном масштабе, действую-
щим значениям ЭДС, напряжений или токов. На рис. 2.3 изо-
бражена векторная диаграмма напряжения u и тока i, причем
ток отстает от напряжения на угол φ, который на векторной
диаграмме всегда показывается стрелкой, направленной от
вектора тока к вектору напряжения.
Синусоидальную функцию
)tsin(Ee
m
ψ+ω
=
можно
изобразить вектором (рис. 2.4) на комплексной плоскости или
записать в виде комплексного числа в показательной форме:
ψ
=
j
m
e
2
E
E
&
, где
2
E
E
m
= – модуль комплексного числа,
равный действующему значению синусоидальной функции,
который на векторной диаграмме соответствует длине вектора
в выбранном масштабе напряжений; ψ – аргумент комплексно-
го числа, соответствующий начальной фазе синусоидальной
функции, которая на комплексной плоскости откладывается от
положительного направления оси действительных чисел;
j =
1−
– мнимая единица.
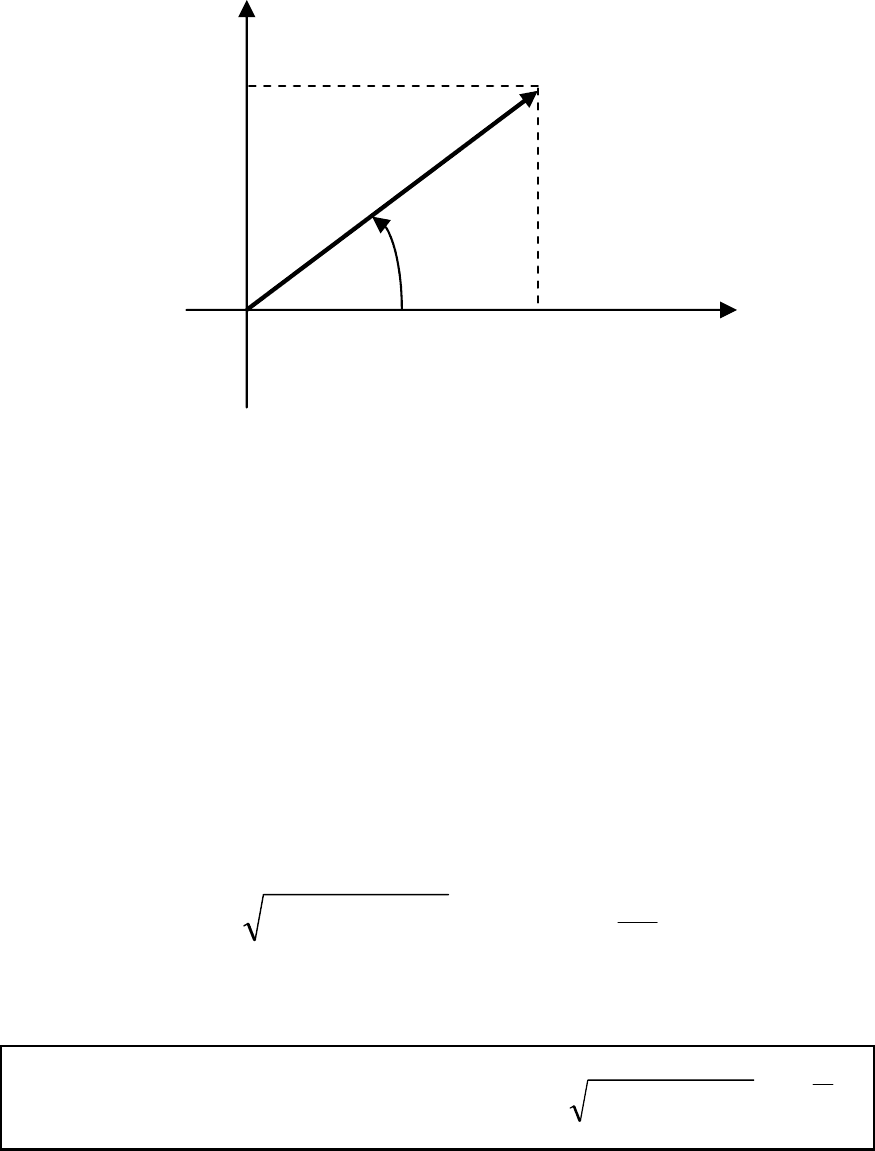
49
Комплексная величина в соответствии с формулой Эйле-
ра может быть записана также в тригонометрической и алгеб-
раической формах записи:
,EjEsinjEcosEEeE
j
′′
+
′
=ψ⋅+ψ⋅==
ψ
&
где
ψ⋅=
′
cosEE
- действительная часть комплексного числа;
ψ⋅=
′′
sinEE
- мнимая часть комплексного числа.
Для обратного перехода от алгебраической к показательной
форме записи необходимо найти модуль этого комплексного
числа с помощью теоремы Пифагора (рис. 2.4) и аргумент пу-
тем определения тангенса соответствующего угла:
22
)E()E(E
′′
+
′
= ,
E
E
arctg
′
′
′
=ψ .
Тогда полностью все формы записи комплексной вели-
чины и связь между ними можно записать:
Тогда векторная диаграмма представляет собой
совокупность векторов токов и напряжений, построенных на
комплексной плоскости.
.e)E()E(EjEsinjEcosEEeE
E
E
jarctg
22j
′
′′
ψ
′′
+
′
=
′′
+
′
=ψ⋅+ψ⋅==
&
+1
+j
Ė
ψ
E·cosψ = E'
E·sinψ = E"
Рис. 2.4
