Пилиди В.С. лекции по высшей математике

Подождите немного. Документ загружается.

ПРИМЕР. Исследовать на сходимость ряд

( )

+∞

−

∑

В силу условия

, получаем, что

e −>

n∈

, рассматри-

ваемый ряд состоит из положительных членов. Остается заметить, что, в

силу эквивалентности

−

при

n → +∞

(или, для более точного со-

поставления с формулировкой теоремы), соотношения

lim 1

→∞

−

следует, что рассматриваемый ряд и гармонический ряд

+∞

∑

сходятся или

расходятся одновременно. Следовательно, рассматриваемый ряд, расхо-

дится.

РИМЕР. Рассмотрим ряд

+∞

∑

в предположении, что

. Из

оценки

≥

n∈

и расходимости гармонического ряда следует, что

ряд

+∞

∑

при указанных значениях параметра

также расходится.

Глава 2

Числовые ряды

4. Признак д’Аламбера

ТЕОРЕМА 5 (ПРИЗНАК Д’АЛАМБЕРА). Пусть

+∞

∑

— ряд с положи-

тельными членами.

1) Если существуют число

01q<<

и такой номер

, что для

всех

nN≥

выполняется неравенство

≤

, то рассматриваемый ряд

сходится.

2) Если существует такой номер

, что для всех

nN≥

выполняет-

ся неравенство

≥

, то рассматриваемый ряд расходится.

ОКАЗАТЕЛЬСТВО. 1) Заменяя рассматриваемый ряд его остатком,

можно предполагать, что неравенство

≤

выполняется для всех зна-

чений

. Тогда

≤

a aq≤⋅

, и далее:

≤

32 1

a aqaq≤ ⋅≤ ⋅

, … .

Методом полной математической индукции легко доказать, что для любо-

го

n∈

выполняется неравенство

a aq

−

≤⋅

. Отсюда и из сходимости

ряда

+∞

−

⋅

∑

следует сходимость ряда

+∞

∑

2) Если, для всех

nN≥

выполняется неравенство

≥

, то для

этих значений

1nn

≤

, и получаем:

NN N

aa a

<≤ ≤ ≤

Глава 2

Числовые ряды

Д'Аламбер

Отсюда следует, что необходимое условие сходимости ряда

lim

→∞

выполняться не может и, следовательно, ряд расходится.

Обычно признак д’Аламбера применяется в следующей форме.

ЕОРЕМА 6 (ПРИЗНАК Д’АЛАМБЕРА В ПРЕДЕЛЬНОЙ ФОРМЕ). Пусть

+∞

∑

— ряд с положительными членами. Если существует конечный предел

lim ,

→+∞

то рассматриваемый ряд сходится, если

1q <

и расходится, если

1q >

ОКАЗАТЕЛЬСТВО. Предположим, что

1q <

. Выберем произвольное

число

, удовлетворяющее неравенству

1qQ<<

и найдем такое

, что

для всех

nN≥

. Тогда по предыдущей теореме рассматриваемый

ряд сходится.

Если

1q >

, то существует такое

, что

для всех

nN≥

, и,

снова применяя предыдущую теорему, получаем, что ряд расходится.

Теорема доказана.

АМЕЧАНИЕ 1. Утверждение последней теоремы может быть не-

сколько уточнено: если

lim

→+∞

= +∞

, то ряд также является расходя-

Глава 2

Числовые ряды

щимся. Действительно, в этом случае неравенство

также выполня-

ется для всех достаточно больших значений

АМЕЧАНИЕ 2. Отметим также, что как для сходящегося, так и расхо-

дящегося ряда предел

lim

→+∞

может вообще не существовать. На-

пример, ряд

2 (2 ( 1) )

−

+∞

+−

∑

мажорируется сходящимся рядом

+∞

⋅

∑

и, следовательно, сходится. Од-

нако

, если

четное,

, если

нечетное, и, следовательно,

lim

→+∞

не существует.

Приведем некоторые примеры.

РИМЕР. Рассмотрим ряд

+∞

∑

в предположении, что

0a >

. Вос-

пользуемся признаком д’Аламбера (в предельной форме):

( 1)!

lim lim 0,

→+∞ →+∞

= =

и ряд является сходящимся.

Глава 2

Числовые ряды

ПРИМЕР. Рассмотрим ряд

+∞

∑

. Тогда

( 1)!

( 1)

lim lim 1 1,

−

→+∞ →+∞



= +=<





и ряд сходится.

АМЕЧАНИЕ. Случай

1q =

не рассматриваемся в признаке д’Аламбе-

ра. В этом случае ряд может как сходиться, так и расходиться. Действи-

тельно, для (расходящегося) гармонического ряда имеем:

lim lim 1.

→+∞ →+∞

= =

С другой стороны, как будет доказано ниже, ряд

+∞

∑

сходится. Для этого

ряда соответствующий предел существует и также равен единице.

5. Признак Коши

ТЕОРЕМА 7 (ПРИЗНАК КОШИ). Пусть

+∞

∑

— ряд с неотрицательны-

ми членами.

Глава 2

Числовые ряды

1) Если существуют число

01q<<

и такой номер

, что для

всех

nN≥

выполняется неравенство

aq≤

, то рассматриваемый ряд

сходится.

2) Если существует такой номер

, что для всех

nN≥

выполняет-

ся неравенство

a ≥

, то рассматриваемый ряд расходится.

ОКАЗАТЕЛЬСТВО. 1) Заменяя рассматриваемый ряд его остатком,

можно предполагать, что неравенство

aq≤

выполняется для всех зна-

чений

. Тогда для всех

n∈

выполняется оценка

aq≤

, рассматривае-

мый ряд

+∞

∑

мажорируется сходящимся рядом и, следовательно, сходит-

ся.

2) Если, для всех

nN≥

выполняется неравенство

a ≥

, то для

этих значений

a ≥

, необходимое условие сходимости ряда

lim 0

→+∞

выполняться не может и, следовательно, ряд расходится.

Теорема доказана.

Признак Коши обычно применяется в следующей форме.

ЕОРЕМА 8 (ПРИЗНАК КОШИ В ПРЕДЕЛЬНОЙ ФОРМЕ). Пусть

+∞

∑

— ряд

с неотрицательными членами. Если существует конечный предел

lim

→+∞

, то рассматриваемый ряд расходится, если

1q <

и сходит-

ся, если

1q >

Глава 2

Числовые ряды

ДОКАЗАТЕЛЬСТВО. Предположим, что

1q <

. Выберем произвольное

число

, удовлетворяющее неравенству

1qQ<<

и найдем такое

, что

aQ<

для всех

nN≥

. Тогда по предыдущей теореме рассматриваемый

ряд сходится.

Если

1q >

, то существует такое

, что

a >

для всех

nN≥

, и,

снова применяя предыдущую теорему, получаем, что ряд расходится.

Теорема доказана.

АМЕЧАНИЕ 1. Как и в случае признака д’Аламбера в предельной

форме, утверждение последней теоремы может быть несколько уточнено:

если

lim

→+∞

= +∞

, то ряд также является расходящимся. Действительно,

в этом случае неравенство

a >

также выполняется для всех достаточно

больших значений

АМЕЧАНИЕ 2. В случае, когда

lim 1

→+∞

ряд может как сходиться,

так и расходиться.

АМЕЧАНИЕ 3. Признак Коши сильнее признака д’Аламбера в сле-

дующем смысле: можно доказать, что если существует предел

lim

→+∞

то существует и предел

lim

→+∞

, и эти пределы равны. Поэтому, если

lim 1

→∞

, то уже нет смысла пытаться применить признак Коши. С дру-

гой стороны, возможна ситуация, когда

lim

→+∞

не существует, в то вре-

Глава 2

Числовые ряды

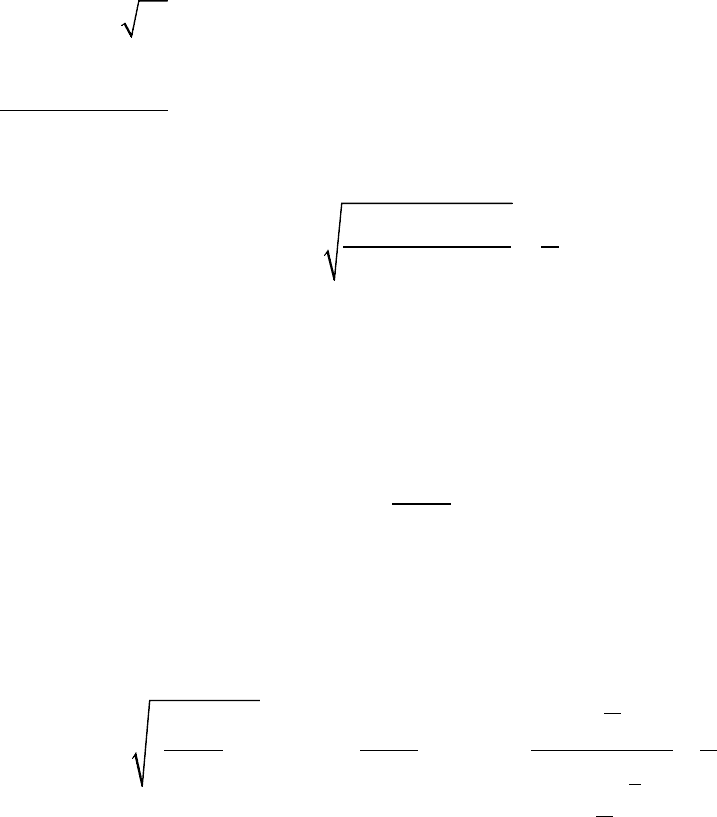
мя как

lim

→+∞

существует. Например, для рассмотренного выше ряда

2 (2 ( 1) )

−

+∞

+−

∑

существует предел

2 (2 ( 1) ) 2

lim ,

−

→+∞

+−

и ряд сходится по признаку Коши. Отметим также, что применение при-

знака д’Аламбера является зачастую технически более удобным.

РИМЕР. Рассмотрим ряд

+∞







∑

Применяем признак Коши:

11 1

lim lim lim 1.

n nn

nn e

→+∞ →+∞ →+∞





 



= = = <

 

 







Следовательно, ряд сходится.

6. Интегральный признак

Предположим, что функция

определена и непрерывна на проме-

жутке

[1, )+∞

, принимает на этом промежутке положительные значения и

является убывающей. Пусть

— произвольная первообразная функ-

Глава 2

Числовые ряды

ции

Отметим, что функция

строго возрастает на рассматриваемом

промежутке (поскольку ее производная положительна).

ЕОРЕМА 9. Ряд

()

+∞

∑

сходится в том и только том случае, когда

существует конечный предел

lim ( )

→+∞

Прежде, чем доказывать теорему, сделаем некоторые замечания.

АМЕЧАНИЕ 1. Первообразная функции определяется ей с точностью

до произвольной постоянной. Однако, если существует предел

lim ( )

→+∞

для некоторой первообразной

()Fx

, то для любой другой первообразной,

необходимо имеющей вид

()Fx C+

, где

— некоторая константа, соот-

ветствующий предел тоже существует. Иначе говоря, условие существова-

ния предела первообразной не зависит от выбора этой первообразной.

АМЕЧАНИЕ 2. В силу возрастания первообразной

условие сущест-

вования конечного предела может быть заменено условием ограниченно-

сти первообразной на промежутке

[1, )+∞

АМЕЧАНИЕ 3. Рассмотрим для функции

первообразную специаль-

ного вида, именно полагаем

( ) ()

F x f t dt=

∫

(поскольку мы предположили,

что функция непрерывна на промежутке

[1, )+∞

, последний определенный

интеграл существует. Если существует конечный предел

lim ( ) ,

f t dt

→+∞

∫

функция

называется интегрируемой в несобственном смысле на проме-

жутке

[1, )+∞

, а сам предел называется несобственным интегралом и обо-

Глава 2

Числовые ряды

значается следующим образом:

()f t dt

+∞

∫

. Говорят также, что в этом случае

указанный несобственный интеграл сходится. Теория таких интегралов

будет рассматриваться ниже. Отметим здесь, что в этих терминах инте-

гральный признак может быть переформулирован так.

Ряд

()

+∞

∑

сходится в том и только том случае, когда сходится

несобственный интеграл

()f t dt

+∞

∫

Перейдем теперь к доказательству теоремы.

ОКАЗАТЕЛЬСТВО ИНТЕГРАЛЬНОГО ПРИЗНАКА. Введем следующие обо-

значения:

()

a fn=

∑

1n =

, 2, … .

Для произвольного числа

k ∈

, и произвольной точки

[ , 1]x kk∈+

, в

силу убывания функции

, имеем:

(1)()().fk fx fk+≤ ≤

Беря определенный интеграл от

до

1k +

, и пользуясь простейшими

свойствами интеграла, отсюда получаем:

1 11

(1)()(),

k kk

f k dx f x dx f k dx

+ ++

+≤ ≤

∫ ∫∫

и далее:

Глава 2

Числовые ряды