Пилиди В.С. лекции по высшей математике
Подождите немного. Документ загружается.

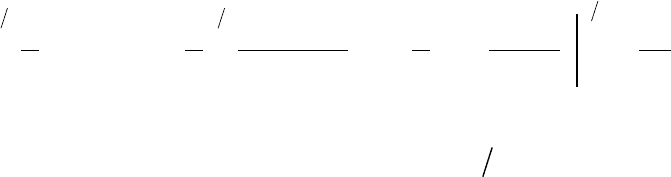
Площадь половины одного из «лепестков», то есть одной шестой части
фигуры, равна
6
66
2
00
0
1 1 1 cos6 1 sin6
sin 3 .
2 2 2 4 6 24
dd
π
ππ
ϕ ϕπ
ϕϕ ϕ ϕ
−
= =−=
∫∫
Отсюда получаем, что площадь всей фигуры равна
4
π
.
Рассмотрим вопрос о вычислении длины дуги кривой. Площадь фи-
гуры определялась как предел площадей более простых фигур, прибли-
жающих данную в некотором смысле. В случае кривых на плоскости по-
ступают аналогично, приближая произвольную кривую ломаной, длина
которой определяется как сумма длин составляющих ее звеньев.
Перейдем к точным определениям.
О
ПРЕДЕЛЕНИЕ. Предположим, что функции
ϕ
и
ψ
непрерывны на
некотором отрезке
[,]ab
. Множество точек координатной плоскости
L
, за-
даваемое условием
{( ( ), ( )): [ , ]}L t t t ab
ϕψ
= ∈
,
называется непрерывной кривой на плоскости.
Рассмотрим указанную в определении кривую
L
. Выберем произ-
вольное разбиение
0
{}
k
ii
t
λ
=
=
отрезка
[,]ab
и рассмотрим последователь-
ность точек
( ( ), ( ))
i ii
M tt
ϕψ
=
,
0i =
, 1, …,
k
этой кривой. Соединяя отрез-
ком каждую точку
i
M
с точкой
1i
M
+
при
0i =
, 1, …,
1k −
, получим неко-
торую ломаную на плоскости, которую будем обозначать через
L
λ
. Обо-
Глава 1
61
Определенный интеграл
ç
è
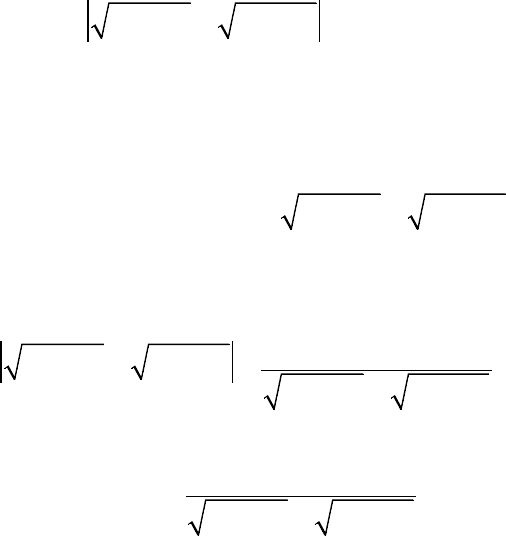
значим через
()L
λ
длину этой ломаной, то есть сумму длин составляющих
ее отрезков, звеньев этой ломаной.
О
ПРЕДЕЛЕНИЕ. Непрерывная кривая на плоскости называется спрям-
ляемой, если существует предел
|| 0
lim ( )L
λ
λ
→
. В этом случае указанный пре-
дел называется длиной кривой
L
.
Длину спрямляемой кривой
L
будем обозначать
()L
.
Прежде, чем доказывать теорему о вычислении длины спрямляемой
кривой, докажем следующее вспомогательное утверждение.
Л
ЕММА. Для любых вещественных
a
,
b
,
c
имеет место оценка
22 22
| |.a c b c ab+ − + ≤−
Д
ОКАЗАТЕЛЬСТВО. Если
0ab= =
, то доказываемое соотношение, оче-
видно, имеет место. Допустим, что числа
a
и
b
не обращаются в ноль од-
новременно. Умножая и деля разность
22 22
ac bc+− +
на сопряженное
выражение, находим:
22
22 22
22 22
||ab
ac bc
ac bc
−
+− + ≤ =
++ +
22 22
||
|| .
ab
ab
ac bc
+
= −
++ +
(∗)
Оценим дробь в правой части. Учтем следующие соотношения:
| || | | |ab a b+≤ +
,
Глава 1
62
Определенный интеграл
ç
è

22 22 2 2
| | | |.ac bc a b a b++ +≥ + =+
Следовательно,
22 22
||
1,
ab
ac bc
+
≤
++ +
и из (∗) получаем искомое неравенство.
Лемма доказана.
Т
ЕОРЕМА 17. Предположим, что кривая на плоскости задается ус-
ловием
{( ( ), ( )): [ , ]},L t t t ab
ϕψ
= ∈
где функции
ϕ
и
ψ
определены и непре-
рывно дифференцируемы на отрезке
[,]ab
. Тогда кривая
L
является
спрямляемой, и ее длина может быть найдена по формуле
22
( ) ( ( )) ( ( )) .
b
a
L t t dt
ϕψ
′′
= +
∫
Д
ОКАЗАТЕЛЬСТВО. Следуя определению спрямляемой кривой, выбе-
рем произвольное разбиение
0
{}
k
ii
t
λ
=
=
отрезка
[,]ab
, введем последова-
тельность точек
( ( ), ( ))
i ii
M tt
ϕψ
=
,
0i =
, 1, …,
k
и соединим отрезком каж-
дую точку
i
M
с точкой
1i
M
+
при
0i =
, 1, …,
1k −
. Длину отрезка
1ii
MM
+
находим по формуле
22
11 1
| | ( ( ) ( )) ( ( ) ( )) .
ii i i i i
MM t t t t
ϕϕ ψψ
++ +
= −+ −
Тогда длина ломаной
L
λ
, которая получается путем последовательного со-
единения этих отрезков, равна
Глава 1
63
Определенный интеграл
ç
è
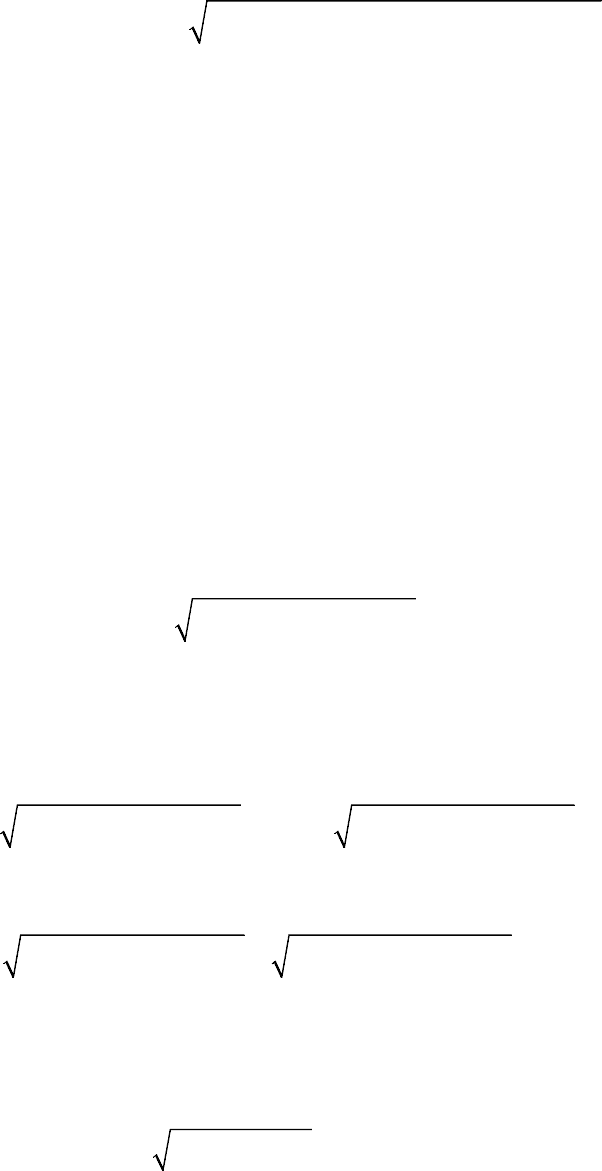
11
22
11 1
00
( ) | | ( ( ) ( )) ( ( ) ( ))
kk
ii i i i i
ii
L MM t t t t
λ
ϕϕ ψψ
−−
++ +
= =
= = −+ −
∑∑
Применяя к каждой из разностей
1
( ) ()
ii
tt
ϕϕ
+
−
,
0i =
, 1, …,
1k −
формулу
конечных приращений, получаем:
1
( ) () ( ) ,
i i ii
tt t
ϕ ϕ ϕξ
+
′
−= ∆
где
i
ξ
— неко-
торая точка, принадлежащая отрезку
1
[, ]
ii
tt
+
,
1ii i
tt t
+
∆= −
. Набор точек
1
0
{}
k
ii
ξξ
−
=
=
подчинен разбиению
λ
. Аналогично, рассматривая разность
1
( ) ()
ii
tt
ψψ
+
−
находим точки
1
[, ]
i ii
xx
η
+
∈
, для которых выполняется равен-
ство
1
( ) () ( )
i i ii
tt t
ψ ψ ψη
+
′
−= ∆
. Набор точек
1
0
{}
k
ii
ηη
−
=
=
также подчинен раз-
биению
λ
. Учитывая полученные соотношения, преобразуем формулу для
нахождения
()L
λ
:
1
22
0
( ) ( ( )) ( ( )) .
k
i ii
i
Lt
λ
ϕξ ψη
−
=
′′
= +∆
∑
Преобразуем последнюю сумму следующим образом:
11
22 22
00
( ) ( ( )) ( ( )) ( ( )) ( ( ))
kk
i ii i ii
ii
L tt
λ
ϕξ ψη ϕξ ψξ
−−
= =
′′ ′′
= + ∆= + ∆+
∑∑
( )
1
22 22
0
( ( )) ( ( )) ( ( )) ( ( )) .
k
i i i ii
i
t
ϕξ ψη ϕξ ψξ
−
=
′′ ′′
+ +− + ∆
∑
Первое слагаемое в правой части является интегральной суммой
22
(( ) ( ),,)S
ϕ ψ λξ
′′
+
.
Обозначая второе слагаемое через
(,,)R
λξη
, полученное соотношение пе-
реписываем так:
Глава 1
64
Определенный интеграл
ç
è
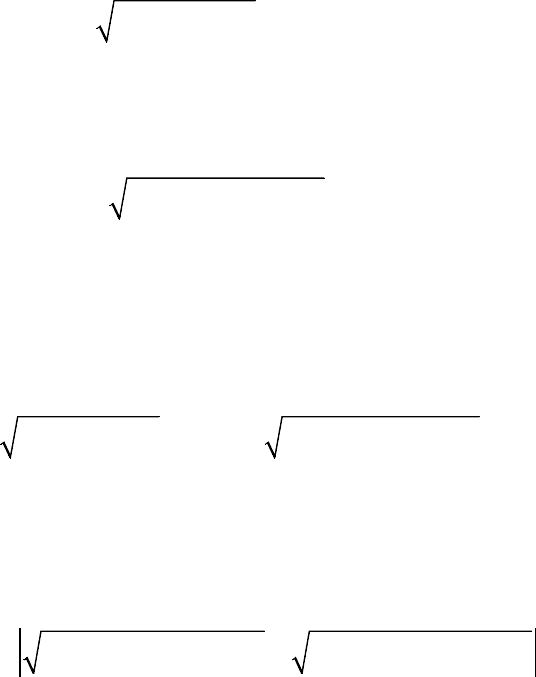
22
( ) (() ( ),,) (,,).LS R
λ
ϕ ψ λξ λξη
′′
=++
(∗)
Найдем предел выражения в правой части при
|| 0
λ
→
. Функция
22
( ( )) ( ( ))tt
ϕψ
′′
+
непрерывна на отрезке
[,]ab
и, следовательно, интегрируема на этом от-
резке. Поэтому выполняется равенство
22 2 2
|| 0
lim ( ( ) ( ) , , ) ( ( )) ( ( )) .
b
a
S t t dt
λ
ϕ ψ λξ ϕ ψ
→
′′ ′ ′
+=+
∫
Для анализа
(,,)R
λξη
, пользуясь леммой, получаем оценку:
1
22 22
0
| ( , , )| ( ( )) ( ( )) ( ( )) ( ( ))
k
i i i ii
i
Rt
λξη ϕξ ψη ϕξ ψξ
−
=
′′ ′′
= + − + ∆≤
∑
11
1
00
| ( ) ( )| ( ,[ , ])
kk
i i i ii i
ii
t tt t
ψ η ψ ξ ωψ
−−
+
= =
′′ ′
≤ − ∆≤ ∆
∑∑
,
где, как и выше, через
1
( ,[ , ])
ii
xx
ωψ
+
′
обозначено колебание функции
ψ
′
на
отрезке
1
[, ]
ii
xx
+
.
Учтем, что функция
ψ
′
является непрерывной на отрезке
[,]ab
. Вы-
берем произвольное
0
ε
>
. В силу теоремы Кантора, найдется такое
0
δ
>
,
что для любых
1
t
,
2
[,]t ab∈
, удовлетворяющих условию
12
||tt
δ
−<
выпол-
няется неравенство
12
| ( ) ( )|tt
ψψ ε
′′
−<
. Возьмем произвольное разбиение
λ
отрезка
[,]ab
, удовлетворяющее условию
||
λδ
<
. Для любого
0i =
, 1, …,
1k −
имеем:
Глава 1
65
Определенный интеграл
ç
è

1 1 2 12 1
( ,[ , ]) sup{| ( ) ( )|: , }
ii i i
tt t t
ωψ ψτ ψτ ττ ε
++
′ ′′
= − ≤ ≤≤
.
Действительно, имеет место неравенство
1
| || |
ii
tt
λδ
+
−≤ <
, следовательно,
любые точки
1
τ
,
21
[, ]
ii
tt
τ
+
∈
удовлетворяют неравенству
12
||
ττ δ
−<
. Тогда
12
| ( ) ( )|
ψτ ψτ ε
′′
−<
,
и указанная точная верхняя грань не превосходит
ε
(используя непрерыв-
ность функции
ψ
′
, легко доказать, что эта оценка является строгой).
Тогда для произвольного разбиения
λ
, удовлетворяющего условию
||
λδ
<
, получаем оценку
11
1
00
| ( , , )| ( ,[ , ]) ( ).
kk
ii i i
ii
R tt t t b a
λξη ωψ ε ε
−−
+
= =
′
≤ ∆≤ ∆= −
∑∑
Отсюда следует, что
|| 0
lim ( , , ) 0S
λ
λξη
→
=
, и окончательно находим:
22
|| 0
lim ( ) ( ( )) ( ( )) .
b
a
L t t dt
λ
λ
ϕψ
→
′′
= +
∫
Полученное соотношение доказывает, что кривая
L
является спрямляемой,
и дает формулу для нахождения ее длины.
Теорема доказана.
Рассмотрим частные случаи вычисления длины дуги.
Предположим, что кривая
L
задана уравнением, разрешенным отно-
сительно
y
:
()y fx=
,
axb≤≤
, где функция
f
непрерывно дифференци-
Глава 1
66
Определенный интеграл
ç
è

руема на отрезке
[,]ab
. Тогда эта же кривая может быть задана параметри-
ческими уравнениями
, ( ),x t y ft a t b= = ≤≤
.
Применяя теорему, получаем, что данная кривая является спрямляемой, и
ее длина может быть найдена по формуле
22
( ) 1 ( ( )) 1 ( ( )) .
bb
aa
L f t dt f x dx
′′
=+=+
∫∫
Предположим, что кривая
L
задается уравнением в полярной систе-
ме координат:
()rf
ϕ
=
,
αϕβ
≤≤
. Учитывая соотношения
cosxr
ϕ
=
,
sinyr
ϕ
=
, связывающие декартовы и полярные координаты, находим па-
раметрические уравнения рассматриваемой кривой:
()cos, ()sin, .xf yf
ϕ ϕ ϕ ϕ αϕβ
= = ≤≤
Функции
( )cosf
ϕϕ
,
( )sinf
ϕϕ
непрерывно дифференцируемы на
отрезке
[,]
αβ
. После элементарных выкладок находим:
22
(( ( )cos ) ) (( ( )sin ) )
ff
ϕϕ ϕϕ
′′
+=
22
( ()cos ()sin) ( ()sin ()cos)ff ff
ϕϕ ϕϕ ϕϕ ϕϕ
′′
= − ++ =
22
( ( )) ( ( )) ,ff
ϕϕ
′
= +
и тогда
22
() (()) ( ()) .L f fd
β
α
ϕ ϕϕ
′
= +
∫
Глава 1
67
Определенный интеграл
ç
è
Глава 2. Числовые ряды
1. Основные определения
Пусть
1
{}
nn
a
+∞
=
— некоторая числовая последовательность. Рядом
(или, точнее, числовым рядом), составленным из элементов этой последо-
вательности, называется выражение
12
,
n
aa a++++
или
1
n
n
a
+∞
=
∑
. От
обычной суммы, составленной из конечного числа слагаемых, это выраже-
ние отличается наличием бесконечного числа слагаемых. Наша задача со-
стоит в том, чтобы придать этой сумме смысл, сопоставив ей при некото-
рых дополнительных предположениях числовое значение.
Введем в рассмотрение следующие конечные суммы:
11 212 3123 12
, , , , ,,
nn
Sa S aa Saaa S aa a= =+ =++ =+++
или
1
n
nk
k
Sa
=
=
∑
,
n∈
. Суммы
n
S
называются частичными суммами рас-
сматриваемого ряда. Числа
n
a
,
n∈
, называются членами рассматривае-
мого ряда.
ç
è

ОПРЕДЕЛЕНИЕ. Числовой ряд
1
n
n
a
+∞
=
∑
называется сходящимся, если по-
следовательность его частичных сумм
1
{ }
nn
S
+∞
=
сходится. В этом случае
суммой указанного ряды называют число
lim
n
n
SS
→+∞
=
и пишут
1
.
n
n
aS
+∞
=
=
∑
Если последовательность частичных сумм
1
{}
nn
S
+∞
=
расходится, то ряд
1
n
n
a
+∞
=
∑
называется расходящимся.
З
АМЕЧАНИЕ 1. Обратим внимание читателя, что выражение
1
n
n
a
+∞
=
∑
может обозначать как сам ряд, так и его сумму.
З
АМЕЧАНИЕ 2. Как и в случае числовых последовательностей, иногда
удобно предполагать, что члены ряда проиндексированы неотрицательны-
ми целыми числами или целыми числами
n
, удовлетворяющими условию
nm≥
при некотором целом (и не обязательно неотрицательном) значе-
нии
m
.
П
РИМЕР. Пусть
q
— произвольное вещественное число. Рассмотрим
числовой ряд
0
n
n
q
+∞
=
∑
. Рассмотрим сначала случай
1q ≠
. Частичные суммы
ряда имеют следующий вид:
1
1
0
1 11
.
1 11
n
n
kn
n
k
q
Sq q
q qq
+
+
=
−
= = =−⋅
− −−
∑
(∗)
Глава 2
69
Числовые ряды
ç
è

Здесь применена формулу для суммирования геометрической прогрессии.
Из полученной формулы следует, что последовательность
1
{}
nn
S
+∞
=
сходится
в том и только том случае, когда сходится последовательность
0
{}
n
n
q
+∞
=
. Мы
знаем, что эта последовательность сходится тогда и только тогда, когда
| |1q <
, и в этом случае
lim 0
n
n
q
→+∞
=
. Для этих значений
q
из формулы (∗)
находим:
1
lim
1
n
n
S
q
→+∞
=
−
.
Остается рассмотреть случай
1q =
. При этом условии
1
n
Sn= +
, и
последовательность
1
{}
nn
S
+∞
=
расходится. Окончательный вывод: рассматри-
ваемый ряд сходится тогда и только тогда, когда
| |1q <
и при этом условии
0
1
1
n
n
q
q
+∞
=
=
−
∑
.
П
РИМЕР. Рассмотрим ряд
1111−+−+
, или
0
( 1)
n
n
+∞
=
−
∑
. Тогда
01 2 3
1, 110, 1111, 11110,SS S S= =−= =−+= =−+−=
Последовательность частичных сумм имеет следующий вид: 1, 0, 1, 0, … .
Эта последовательность является расходящейся и, следовательно, рассмат-
риваемый ряд расходится.
П
РИМЕР. Рассмотрим ряд
1
1
ln 1
n
n
+∞
=
+
∑
. Тогда
1
ln ln( 1) ln ,
n
n
a nn
n
+
= = +−
Глава 2
70
Числовые ряды
ç
è
