Пилиди В.С. лекции по высшей математике
Подождите немного. Документ загружается.

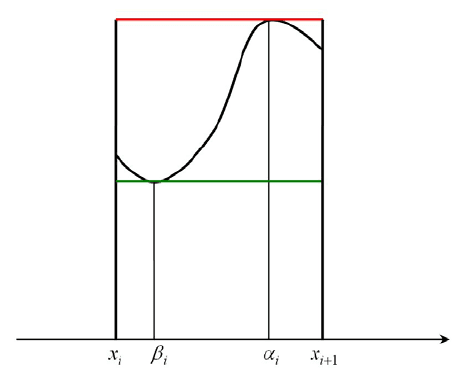
Введем на плоскости следующие фигуры:
()F
λ
+
— объединение
всех прямоугольников с основанием
1
[, ]
ii
xx
+
и высотой
()
i
f
α
,
()F
λ
−
—
объединение всех прямоугольников с основанием
1
[, ]
ii
xx
+
и высотой
( ).
i
f
β
Тогда для любого разбиения
λ
введенные фигуры и рассматривае-
мая криволинейная трапеция
0
F
связаны соотношением
0
() ()F FF
λλ
−+
⊂⊂
.
Площадь фигуры
()F
λ
+
равна сумме площадей всех составляющих ее пря-
моугольников, то есть величине
1
0
()
k
ii
i
fx
α
−
=
∆
∑
. Отметим, что это интеграль-
ная сумма
(;,)Sf
λα
. Аналогично получаем, что площадь фигуры
()F
λ
−
равна
1
0
()
k
ii
i
fx
β
−
=
∆
∑
, то есть интегральной сумме
(;,)Sf
λβ
.
Функция
f
, непрерывная на отрезке
[,]ab
, интегрируема на этом от-
резке. Обозначим:
()
b
a
I f x dx=
∫
. В силу непрерывности функции
f
, вы-
полняются соотношения
Глава 1
51
Определенный интеграл
ç
è
|| 0 || 0
lim ( ; , ) , lim ( ; , ) ,Sf I Sf I
λλ
λα λβ
→→
= =
то есть при
|| 0
λ
→
площади фигур
()F
λ
−
и
()F
λ
+
стремятся к одной и той
же величине.
О
ПРЕДЕЛЕНИЕ. Общий предел значений
(;,)Sf
λα
и
(;,)Sf
λβ
при
|| 0
λ
→
называется площадью криволинейной трапеции
0
.F
В силу сказанного выше, площадь рассматриваемой криволинейной
трапеции равна
()
b
a
f x dx
∫
.
З
АМЕЧАНИЕ. При более строгом подходе вводятся понятия квадри-
руемой фигуры на плоскости и ее площади. Приведем схему одного из ва-
риантов такого подхода. Будем предполагать, что нам известно понятие
площади многоугольника, то есть фигуры, ограниченной замкнутой лома-
ной линией. Площадь многоугольника
F
будем обозначать через
( ).SF
Произвольная фигура
0
F
на плоскости называется квадрируемой, если су-
ществуют последовательности
1
{}
nn
F
− +∞
=
и
1
{}
nn
F
+ +∞
=
многоугольников, обла-
дающие следующими свойствами: для любого
n∈
выполняются вложе-
ния
0nn
F FF
−+
⊂⊂
и имеет место равенство
lim ( ) lim ( )
nn
nn
SF SF
−+
→+∞ →+∞
=
. По-
следнее значение считается площадью квадрируемой фигуры
0
F
. Отметим,
что это определение нуждается в обосновании: нужно показать, что ука-
занный предел не зависит от выбора последовательностей
1
{}
nn
F
− +∞
=
и
1
{}
nn
F
+ +∞
=
, обладающих приведенными свойствами.
Вернемся к введенному выше понятию площади криволинейной тра-
пеции. При любом разбиении
λ
отрезка
[,]ab
фигуры
()F
λ
−
и
()F
λ
+
яв-
Глава 1
52
Определенный интеграл
ç
è
ляются многоугольниками, связанными с рассматриваемой криволинейной
трапецией соотношением
0
() ()F FF
λλ
−+
⊂⊂
. Одинаковые пределы пло-
щадей этих многоугольников при
|| 0
λ
→
мы и назвали площадью этой
криволинейной трапеции. При этом не анализировались другие способы
приближения криволинейной трапеции многоугольниками «снаружи» и
«изнутри».
Остановимся теперь совсем кратко на других вариантах вычислений
площадей плоских фигур.
Предположим, что даны две функции
f
и
g
, которые определена и
непрерывны на отрезке
[,]ab
, причем для любого
[,]x ab∈
выполняется
неравенство
() ()gx fx≤
. Рассмотрим фигуру, ограниченную осью
Ox
,
прямыми
xa=
,
xb=
и линиями
()y fx=
,
()y gx=
,
axb≤≤
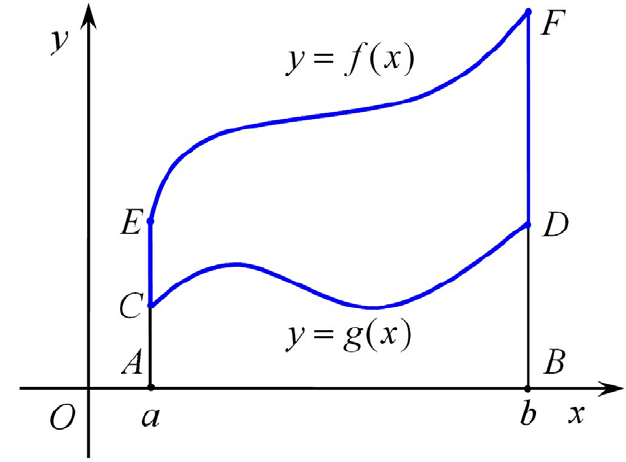
. На приво-
димом ниже рисунке эта фигура ограничена линиями синего цвета.
Площадь данной фигуры является разностью площадей криволиней-
ных трапеций
ABFE
и
ABDC
, то есть разности
Глава 1
53
Определенный интеграл
ç
è
() () ( () ()) .
bbb
aaa
f x dx g x dx f x g x dx
−=−
∫∫∫
З
АМЕЧАНИЕ. Полученная формула найдена в предположении, что обе
функции
f
и
g
принимают на отрезке
[,]ab
неотрицательные значения
(поскольку была использована формула для нахождения площади криво-
линейной трапеции, выведенная именно при таком предположении). Одна-
ко формула для нахождения площади фигуры, ограниченной двумя линия-
ми, остается в силе и без предположения о том, что функции
f
и
g
при-
нимают неотрицательные значения. Действительно, в последнем случае
найдется такая положительная константа
c
, что функции
fc+
и
gc+
принимают на отрезке
[,]ab
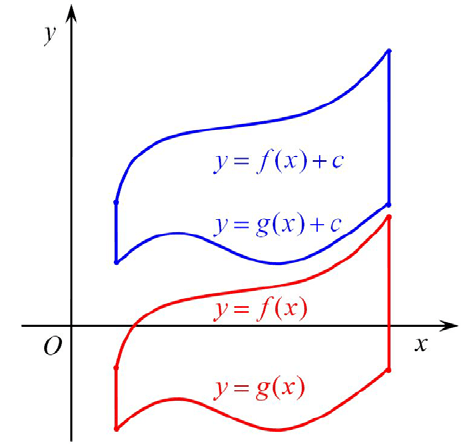
положительные значения. При этом анализи-
руемая фигура сдвинется на
c
единиц параллельно оси ординат (см. рису-
нок ниже). Площади фигуры сохраняется при параллельном переносе.
Применяя к фигуре, полученной после сдвига (и имеющей ту же площадь,
что и исходная фигура), приведенную выше формулу, находим, что эта
площадь равна
Глава 1
54
Определенный интеграл
ç
è
( () ) (() ) ( () ()) ,
bbb
aaa
f x c dx g x c dx f x g x dx+− += −
∫∫∫
то есть формула для нахождения площади остается верной и в рассматри-
ваемом случае.
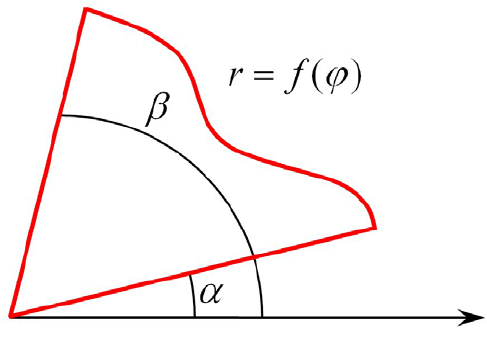
Перейдем теперь к вопросу о площади криволинейного сектора. Вы-
берем на плоскости полярную систему координат и введем кривую, задан-
ную в этой системе координат уравнением
()rf
ϕ
=
,
αϕβ
≤≤
,
где
02
αβ π
≤<≤
,
f
— функция, определенная и непрерывная на отрезке
[,]
αβ
и принимающая всюду на этом отрезке неотрицательные значения.
Рассмотрим на плоскости фигуру, ограниченную данной линией и
лучами
ϕα
=
,
ϕβ
=
. Эта фигура называется криволинейным сектором
(см. рисунок ниже). Обозначим рассматриваемый криволинейный сектор
через
0
F
.
В случае криволинейной трапеции рассматриваемая фигура приближалась
объединением прямоугольников. Криволинейный сектор мы будем при-
Глава 1
55
Определенный интеграл
ç
è
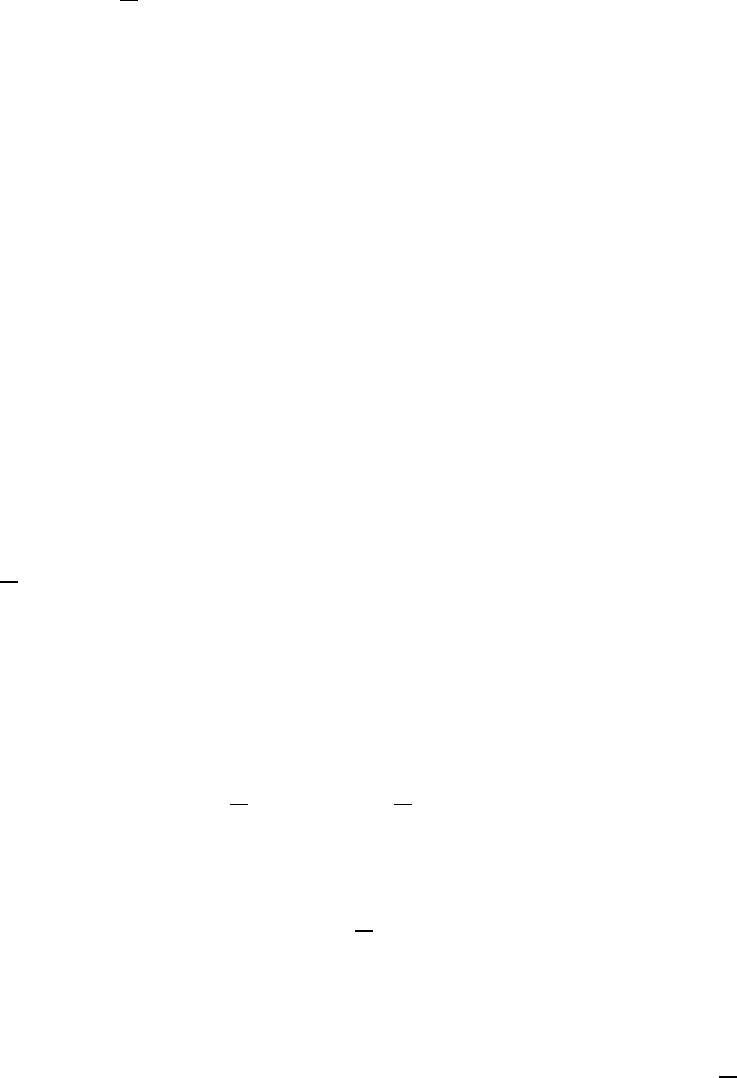
ближать объединением круговых секторов. Напомним, что площадь круго-
вого сектора радиуса
R
с центральным углом
ϕ
(как всегда, измеряемым в
радианах) равна
2
1
2
R
ϕ
.
Пусть
0
{}
k
ii
λϕ
=
=
— произвольное разбиение отрезка
[,]
αβ
. Предпо-
ложим, что сужение функции
f
на отрезок разбиения
1
[, ]
ii
ϕϕ
+
,
0i =
, 1, …,
1k −
принимает свое наибольшее значение на этом отрезке в точке
1
[ , ]
i ii
α ϕϕ
+
∈
, а в точке
1
[, ]
i ii
β ϕϕ
+
∈
принимает свое наименьшее значение.
Обозначим
()
ii
fM
α
=
,
()
ii
fm
β
=
. Введем наборы точек
1
0
{} ,
k
ii
αα
−
=
=
1
0
{}
k
ii
ββ
−
=
=
. Тогда выполняются соотношения
|
αλ
,
|
βλ
.
Для каждого
0i =
, 1, …,
1k −
рассмотрим круговой сектор радиу-
са
i
M
, ограниченный лучами
i
ϕϕ
=
и
1i
ϕϕ
+
=
. Площадь такого сектора
равна
2
1
2
ii
M
ϕ
∆
, где
1ii i
ϕϕ ϕ
+
∆= −
. Обозначим через
()F
λ
+
объединение
всех таких секторов. Тогда площадь фигуры
()F
λ
+
равна сумме состав-
ляющих ее круговых секторов, то есть равна
11
2
00
11
()
22
kk
ii i i
ii
Mf
ϕ αϕ
−−
2
= =
∆= ∆
∑∑
.
Это интегральная сумма
2
1
;,
2
Sf
λα
. Аналогично для каждого
0i =
, 1, …,
1k −
рассматриваем круговые секторы радиуса
i
m
, ограничен-
ные лучами
i
ϕϕ
=
и
1i
ϕϕ
+
=
. Площадь такого сектора равна
2
1
.
2
ii
m
ϕ
∆
Пусть через
()F
λ
−
— объединение всех таких секторов. Тогда площадь
фигуры
()F
λ
−
равна
Глава 1
56
Определенный интеграл
ç
è
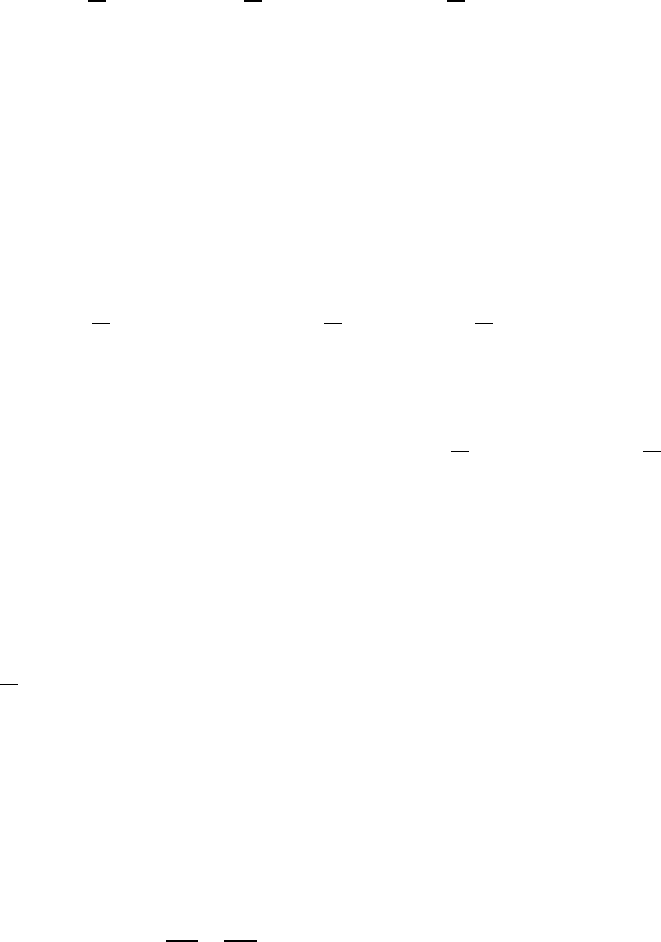
11
22
00
11 1
( ) ;, .
22 2
kk
ii i i
ii
m f Sf
ϕ β ϕ λβ
−−
2
= =
∆= ∆=
∑∑
Остается заметить, что для любого разбиения
λ
отрезка
[,]
αβ
вы-
полняется соотношение
0
() ()F FF
λλ
−+
⊂⊂
и, кроме того, для площадей
фигур
()F
λ
−
и
()F
λ
+
выполняется соотношение
2 22
|| 0 || 0
1 11
lim ; , lim ; , ( ) .
2 22
Sf Sf f d
β
λλ
α
λα λβ ϕ ϕ
→→
= =
∫
О
ПРЕДЕЛЕНИЕ. Общий предел значений
2
1
;,
2
Sf
λα
и
2
1
;,
2
Sf
λβ
при
|| 0
λ
→
называется площадью криволинейного сектора
0
F
.
В силу сказанного, площадь рассматриваемого криволинейного сек-
тора равна
2
1
() .
2
fd
β
α
ϕϕ
∫
Перейдем к примерам.
П
РИМЕР. Найти площадь, ограниченную эллипсом, задаваемым ка-
ноническим уравнением
22
22
1
xy
ab
+=
.
Р
ЕШЕНИЕ. В силу симметричности эллипса относительно осей коор-
динат, достаточно вычислить площади фигуры, ограниченной эллипсом и
находящейся в первой координатной четверти.
Глава 1
57
Определенный интеграл
ç
è
Уравнение части эллипса, находящейся в первой четверти, имеет вид:
2
2
1 ,0 ,
bx
y xa
a
a
= − ≤≤
и площадь указанной части эллипса находим как площадь криволинейной
трапеции:
22 22
00
.
aa
bb
a x dx a x dx
aa
−=⋅−
∫∫
В последнем интеграле выполним замену переменной:
sinxa t=
,
0
2
t
π
≤≤
.
Тогда
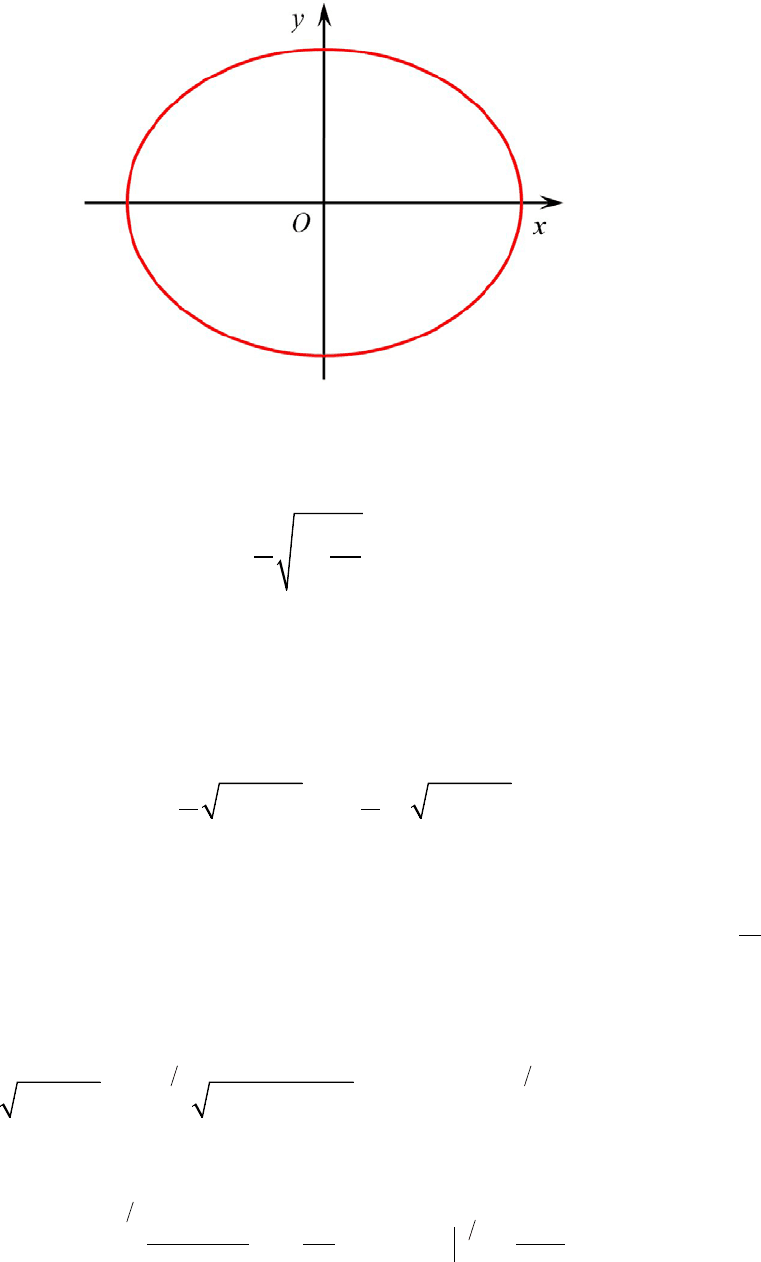
22
2 2 2 22 2
2
00 0
sin ( sin ) cos
a
a x dx a a t d a t a tdt
ππ
−= − = =
∫∫ ∫
2
22
2
2
0
0
1 cos2
( sin2 ) .
22 4
ta a
a dt t t
π
π
π
+
= =+=
∫
Глава 1
58
Определенный интеграл
ç
è
Окончательно находим формулу для нахождения площади
S
рассматри-
ваемого эллипса:
2
4.
4
ba
S ab
a
π
π
=⋅⋅ =
П
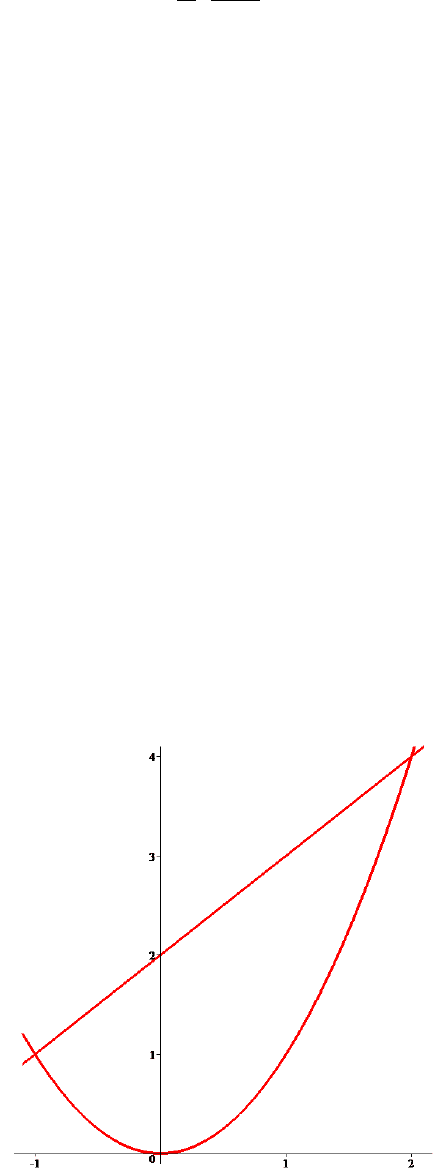
РИМЕР. Найти площадь фигуры, ограниченной линиями
2
yx=
и
3yx= +
.
Р
ЕШЕНИЕ. Найдем точки пересечений указанных линий. Для этого
рассматриваем систему уравнений
2
,
2.
yx
yx
=
= +
Исключаем неизвестную
y
:
2
2xx= +
,
2
20xx−−=
. Отсюда находим
абсциссы точек пересечения:
1
1x = −
,
2
2x =
. При
12x−< <
выполняется
неравенство
2
2xx+>
, то есть точки прямой находятся выше точек пара-
болы с теми же абсциссами (см. рисунок ниже).
Глава 1
59
Определенный интеграл
ç
è
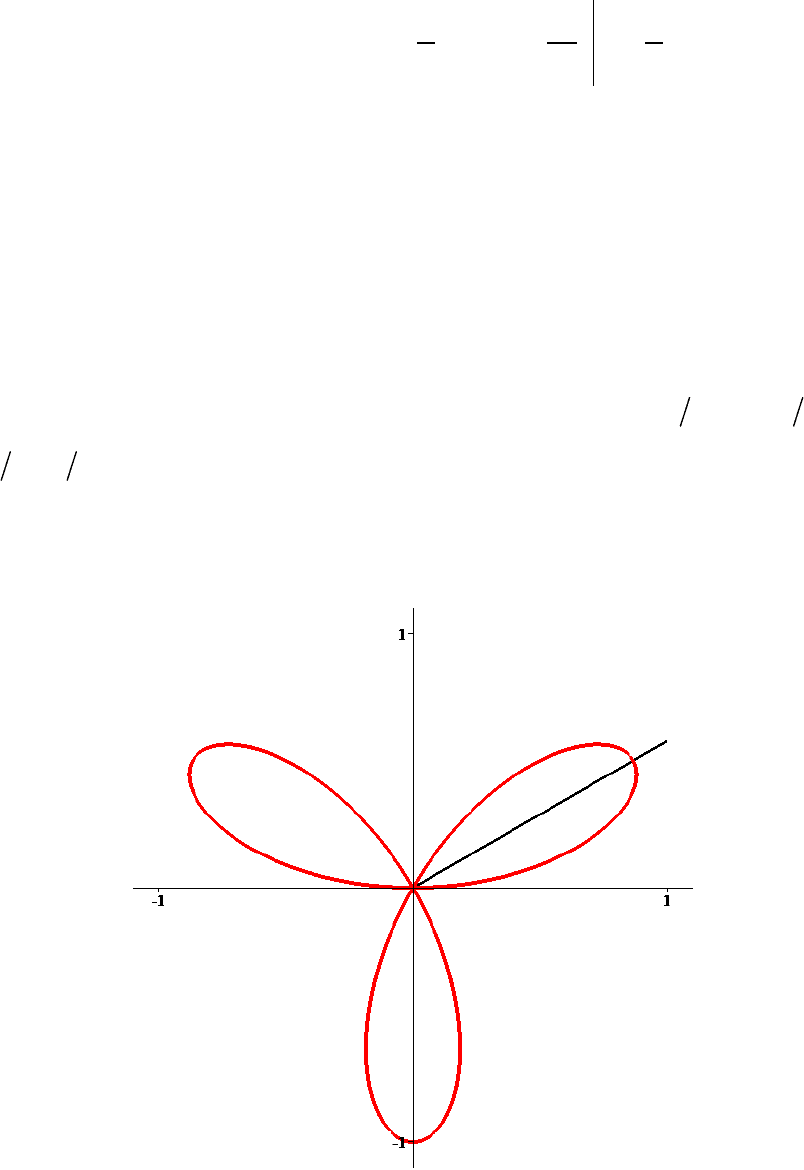
Теперь находим искомую площадь:
2
2
3
22
1
1
19
(2 ) 2 .
2 32
x
S x x dx x x
−
−
= +− = + − =
∫
П
РИМЕР. Вычислить площадь фигуры, ограниченной линией
cos3 , 0 2 .r
ϕ ϕπ
= ≤≤
Р
ЕШЕНИЕ. Точки кривой соответствуют тем и только тем значениям
полярного угла
ϕ
, для которых выполняется неравенство
sin3 0
ϕ
≥
, то
есть значениям
ϕ
, принадлежащим промежуткам
[0, 3]
π
,
[2 3, ]
ππ
,
[4 3,5 3]
ππ
. При этом площади всех трех «лепестков» рассматриваемой
фигуры совпадают (см. рисунок ниже).
Глава 1
60
Определенный интеграл
ç
è
