Пилиди В.С. лекции по высшей математике

Подождите немного. Документ загружается.

где введено обозначение

| () ()|K fc gc= −

Полученное неравенство остается верным и для случая

∉

, по-

скольку тогда левая часть равна нулю. Перепишем это неравенство сле-

дующим образом:

(;,) | | (;,) (;,) | |.Sg K Sf Sg K

λξ λ λξ λξ λ

−⋅ ≤ ≤ +⋅

(∗∗)

Допустим, что функция

интегрируема на промежутке

[,]ab

, то

есть существует

| | 0, |

lim ( ; , )I Sg

λ ξλ

λξ

→

. Учитывая, что

| | 0, |

lim ( ( ; , ) | |)Sg K I

λ ξλ

λξ λ

→

±⋅ =

из (∗∗) находим, что

| | 0, |

lim ( ; , )Sf I

λ ξλ

λξ

→

, то есть функция

интегрируема

на отрезке

[,]ab

и имеет место равенство

() () .

f x dx g x dx=

∫∫

Теорема доказана.

3. Критерий интегрируемости функции

В этом разделе будет дан критерий интегрируемости функции и до-

казана интегрируемость функций некоторых классов. Поскольку мы дока-

зали, что неограниченная функция интегрируемой не является, будут рас-

сматриваться только ограниченные функции.

Глава 1

Определенный интеграл

Предположим, что функция

определена и ограничена на отрез-

ке

[,]ab

. Выберем произвольное разбиение

{ } ([ , ])

x ab

= ∈Λ

. Введем

следующие обозначения:

( , ) inf{ ( ): }, ( , ) sup{ ( ): },

i ii i ii

mf fx x x x M f fx x x x

λλ

= ≤≤ = ≤≤

где

0i =

, …,

1k −

В дальнейшем обозначения

(,)

будем сокращать до

. Аналогично

будем поступать для обозначения

(,)

ПРЕДЕЛЕНИЕ. Верхней суммой Дарбу называется сумма

(;) .

Sf Mx

−

∗

= ∆

∑

Нижней суммой Дарбу называется сумма

(;) .

Sf mx

−

∗

= ∆

∑

Если ясно, какая функция имеется в виду, обозначение

(;)Sf

∗

бу-

дем сокращать до

()S

∗

. Аналогично для нижней суммы Дарбу.

Отметим следующие свойства сумм Дарбу.

1°. Для любого разбиения

отрезка

[,]ab

и любого подчиненного

этому разбиению набора точек

, выполняется неравенство

(;) (;,) (;).S f Sf S f

λ λξ λ

∗

≤≤

Глава 1

Определенный интеграл

Дарбу

Действительно, пусть

{}

ξξ

−

. Тогда для любого

0,i =

, …,

1k −

имеет место соотношение

[, ]

i ii

∈

и, следовательно, вы-

полняется неравенство

inf ( ) ( ) sup ( ) .

i ii

x xx

m fx f fx M

≤≤

= ≤≤ =

Умножая каждое из полученных неравенств

()

i ii

mf M

≤≤

0i =

…,

1k −

на положительное число

x∆

и суммируя по

от

до

1k −

, нахо-

дим:

11 1

00 0

() .

kk k

ii i i ii

ii i

mx f x Mx

−− −

= = =

∆≤ ∆≤ ∆

∑∑ ∑

Это и есть доказываемое соотношение.

2°. Для любого разбиения

выполняются соотношения

(;) sup(;,), (;) inf(;,).

S f Sf S f Sf

ξξλ

λ λξ λ λξ

∗

= =

(∗)

АМЕЧАНИЕ. Точная верхняя и точная нижняя грани берутся по всем

наборам точек

, подчиненным разбиению

Докажем, например, первое соотношение. Пусть

{}

−

. Выбе-

рем произвольное число

. В силу определения точной верхней грани,

для каждого

0i =

, …,

1k −

найдется такая точка

[, ]

i ii

∈

, что вы-

полняется неравенство

()

ξε

>−

. Набор этих точек

{}

ξξ

−

подчи-

нен разбиению

. Умножая каждое из неравенств

()

ξε

>−

на поло-

жительное число

x∆

, получаем:

Глава 1

Определенный интеграл

( ) , 0,1, , 1.

i i ii i

f x Mx x i k

ξε

∆ > ∆ −∆ = −

Суммируем последние неравенства по всем значениям

1 11

0 00

() ,

k kk

i i ii i

i ii

f x Mx x

ξε

− −−

= = =

∆> ∆− ∆

∑ ∑∑

то есть

(;,) (;) (;) ( ).

Sf Sf x Sf ba

λξ λε λε

−

∗∗

> − ∆= − −

∑

Учитывая произвольность

, неравенство

(;,) (;)Sf S f

λξ λ

∗

≤

и опре-

деление точной верхней грани, получаем окончательное соотношение:

(;) sup(;,)S f Sf

ξλ

λ λξ

∗

Пусть

([ , ])ab

∈Λ

. Разбиение

этого отрезка называется измельче-

нием разбиения

, если каждая точка множества

принадлежит множе-

ству

. В этом случае множество

просто является подмножеством

множества

. Для обозначения этого факта будем использовать обычные

теоретико-множественные обозначения:

λλ

⊂

3°. Если

λλ

⊂

, то

(; ) (; )Sf Sf

λλ

∗∗

≤

(; ) (; )Sf Sf

λλ

∗∗

≥

Иначе говоря, при измельчении разбиения верхняя сумма Дарбу мо-

жет только уменьшиться, а нижняя — только увеличиться.

Глава 1

Определенный интеграл

Рассмотрим первое из указанных соотношений. Очевидно, достаточ-

но ограничиться случаем, когда разбиение

получается из разбиения

путем добавления одной точки. Предположим, что

{}

01 k

ax x x b=<<< =

и между точками

добавляется точка

′

, то есть разбиение

со-

стоит из точек

01 1ll k

ax x x x x x b

′

=<<<<< << =

При переходе от разбиения

к разбиению

изменяется только один из

отрезков разбиения: вместо отрезка

[, ]

возникают два отрезка:

[,]

′

[, ]

′

. Введем следующие обозначения:

sup ( )

x xx

M fx

≤≤ +

1ii i

xx x

∆= −

0i =

, 1, …,

1k −

sup ( )

x xx

M fx

′

≤≤

′

sup ( )

x xx

M fx

′

≤≤

′′

∆= −

′′ ′

∆= −

Из вложения

[,] [, ]

l ll

xx xx

′

⊂

следует, что имеет место соотношение

sup ( ) sup ( )

l ll

x xx x xx

M fx fx M

′

≤≤ ≤≤

′

=≤=

Аналогично получаем вторую оценку:

′′

≤

. Кроме того, выпол-

няется равенство

′ ′′

∆ +∆ =∆

. Выделяя в сумме

()S

∗

слагаемые, соот-

ветствующие отрезкам

[,]

′

[, ]

′

, получаем:

2 00 11 1 1

()

S Mx Mx M Mx M

∗

−−

= ∆+ ∆+ + ∆ +

′ ′ ′′

∆+ +

′′

∆

Глава 1

Определенный интеграл

11 1 1ll kk

Mx Mx

++ − −

+ ∆ ++ ∆ ≤

00 11 1 1

()

ll l

Mx Mx M x M

∆

−

′ ′′

∆ +∆≤ ∆+ ∆+ + ∆ + +







11 1 1ll kk

Mx Mx

++ − −

+ ∆ ++ ∆ =

00 11 1 1l l ll

Mx Mx M x Mx

−−

= ∆+ ∆+ + ∆ + ∆+



11 1 1 1

( ).

ll kk

Mx Mx S

∗

++ − −

+ ∆ ++ ∆ =

В приведенных соотношениях выделенные красным цветом слагае-

мые оцениваются сверху с учетом доказанных выше соотношений

′

≤

′′

≤

. Полученные слагаемые выделены синим цветом.

Аналогично доказывается второе соотношение.

4°. Для любых разбиений

([ , ])ab

⊂Λ

выполняется неравенство

1 2

( ) ( ).SS

λ λ

∗

≤

Действительно, рассмотрим разбиение

([ , ])ab

⊂Λ

, получаемое пу-

тем объединения всех точек разбиений

. Тогда

λλ

⊂

λλ

⊂

и,

100 2

по свойству 3 по свойству 1 по свойству 3

() () () ().SSS S

λλ λ λ

∗∗

≤≤≤

 

Критерий интегрируемости функции дается следующей теоремой.

ЕОРЕМА 3. Пусть

— определенная на отрезке

[,]ab

ограниченная

функция. Тогда следующие условия равносильны:

Глава 1

Определенный интеграл

1) функция

интегрируема на отрезке

[,]ab

;

2) по любому

найдется такое

, что для любого разбие-

ния

отрезка

[,]ab

, удовлетворяющего условию

λε

, выполняется не-

равенство

() ()SS

λ λε

∗

−<

ОКАЗАТЕЛЬСТВО. 1) ⇒ 2) Обозначим:

()

I f x dx=

∫

. Выберем произ-

вольное число

и найдем такое

, что для любого разбие-

ния

([ , ])ab

∈Λ

, удовлетворяющего условию

λδ

, и любого набора то-

чек

ξλ

выполняется неравенство

|(,) |SI

λξ ε

−<

. Последнее неравен-

ство перепишем так:

(,)IS I

ε λξ ε

−< <+

Зафиксируем произвольное разбиение

([ , ])ab

∈Λ

, удовлетворяю-

щее условию

λε

. Неравенство

(,)SI

λξ ε

выполняется для любого

набора точек

ξλ

. Беря в левой части этого неравенства точную верх-

нюю грань по всем наборам точек

указанного вида, получаем, что

sup ( , ) ,SI

ξξλ

λξ ε

≤+

то есть

()SI

λε

∗

≤+

. Аналогично из неравенства

(,)IS

ε λξ

−<

находим, что

()SI

λε

∗

≥−

. Тогда выполняется неравенство



() () ( ) ( ) 2

SS I I

λ λ ε εε

∗

≤+

≥−

− ≤+−−=

В силу произвольности

, требуемое утверждение доказано.

2) ⇒ 1) Для любых разбиений

([ , ])ab

∈Λ

в силу свойства 4º

сумм Дарбу, выполняется неравенство

() ()SS

λλ

∗

≤

. Переходя в левой

части неравенства к точной верхней грани по всем разбиениям

при про-

Глава 1

Определенный интеграл

извольном фиксированном

, получаем, что

sup ( ) ( )SS

λλ

∗

≤

. Теперь,

беря в правой части последнего неравенства точную нижнюю грань по

всем разбиениям

, получаем:

sup ( ) inf ( )SS

λλ

∗

≤

Обозначим:

sup ( )IS

∗∗

inf ( )IS

∗∗

, где точные верхняя и ниж-

няя грани берутся по всем разбиениям отрезка

[,]ab

. Мы доказали, что

имеет место неравенство

∗

≤

Для произвольного разбиения

([ , ])ab

∈Λ

по определению точной

верхней и точной нижней граней имеют место оценки

()SI

∗∗

≤

()IS

∗∗

≤

Комбинируя эти неравенства и неравенство

∗

≤

, находим, что

() ().S IIS

λλ

∗∗

≤≤≤

(∗)

Из этого неравенства следует оценка

0 () ()IIS S

λλ

∗∗

≤−≤ −

Находящаяся в правой части разность

() ()SS

λλ

∗

−

может быть сделана

сколь угодно малой за счет выбора разбиения

. Тогда из последнего не-

равенства получаем, что

∗

. Обозначим:

II I

∗

= =

Из (∗) получаем, что для любого разбиения

([ , ])ab

∈Λ

выполняется

неравенство

() ().S IS

λλ

∗

≤≤

Для произвольного набора точек

, подчи-

Глава 1

Определенный интеграл

ненного разбиению

имеет место неравенство

() (,) ()SS S

λ λξ λ

∗

≤≤

. Из

двух полученных соотношений следует, что обе величины

(,)S

λξ

по-

падают в отрезок

[ ( ), ( )]SS

λλ

∗

. Следовательно, выполняется неравенство

|(,) | () ()S IS S

λξ λ λ

∗

−≤ −

. (∗)

Отсюда вытекает, что

| | 0, |

lim ( , )SI

λ ξλ

λξ

→

. Действительно, выберем

произвольное

и найдем такое

что для всех разбиений

, удов-

летворяющих условию

λδ

, выполняется неравенство

() () .SS

λ λε

∗

−<

Тогда для тех же

и наборов точек

ξλ

из (∗) получаем, что

|(,) |SI

λξ ε

−<

В силу произвольности

, доказательство завершено.

4. Колебание функции

Пусть

—определенная и ограниченная на промежутке

. Колеба-

нием функции

на этом промежутке называется величина

( , ) sup ( ) inf ( ).

fI fx fx

∈

= −

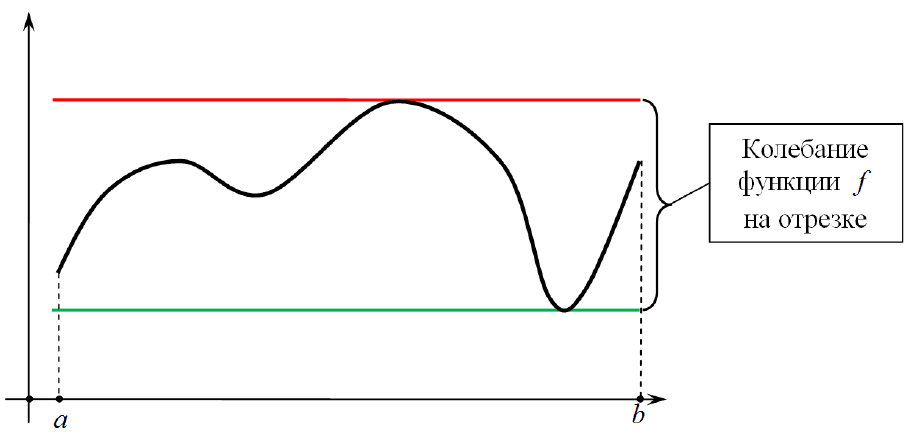
Графическая интерпретация колебания изображена на следующем рисун-

ке. Предполагается, что функция

непрерывна на отрезке

[,]ab

. На ри-

сунке красная прямая задается уравнением

max

, где

max

max ( )

axb

y fx

≤≤

, зе-

леная прямая имеет уравнение

min

yy=

min

min ( )

axb

y fx

≤≤

Глава 1

Определенный интеграл

Отметим некоторые свойства колебания.

1°. Колебание функции является неотрицательным числом. Если

(,) 0fI

, то функция является постоянной на промежутке

Действительно, обозначим:

sup ( )

M fx

∈

inf ( )

m fx

∈

. Тогда

Mm≥

и, следовательно,

(,) 0fI M m

= −≥

. Если

(,) 0fI

, то

Mm=

. Добав-

ляя сюда неравенство

()m fx M≤≤

xI∈

, получаем, что для произволь-

ного

xI∈

()M m fx M=≤≤

, откуда следует, что

()fx M=

xI∈

2°. Имеет место равенство

( , ) sup{| ( ) ( )|: , }.fI fx fx xx I

′ ′′ ′ ′′

=−∈

ОКАЗАТЕЛЬСТВО. Если функция

является постоянной на проме-

жутке

, то левая и правая части доказываемого соотношения равны нулю,

и, следовательно, равенство имеет место.

Глава 1

Определенный интеграл