Пилиди В.С. лекции по высшей математике
Подождите немного. Документ загружается.


ТЕОРЕМА 8 (ПРИЗНАК СРАВНЕНИЯ В ПРЕДЕЛЬНОЙ ФОРМЕ). Предполо-
жим, что функции
f
и
g
определены на промежутке
(,]ab
и интегри-
руемы на отрезке
[ ,]ab
λ
+
для любого
λ
, удовлетворяющего условию
0 ba
λ
<<−
. Допустим, что обе эти функции принимают на промежутке
(,]ab
только положительные значения и существует предел
0
()
lim 0
()
xa
fx
gx
→+
>
. Тогда несобственные интегралы
()
b
a
f x dx
∫
и
()
b
a
g x dx
∫
схо-
дятся или расходятся одновременно.
С
ЛЕДСТВИЕ ТЕОРЕМЫ. Предположим, что функция
f
определена на
промежутке
(,]ab
, принимает на этом промежутке положительные зна-
чения и интегрируемы на отрезке
[ ,]ab
λ
+
для любого
λ
, удовлетворяю-
щего условию
0 ba
λ
<<−
. Предположим, что для некоторого
0
α
>
вы-
полняется равенство
0
lim ( ) ( )
xa
x a fx C
α
→+
−=
, где
0C >
. Тогда при
1
α
<
не-
собственный интеграл
()
b
a
f x dx
∫
сходится, а при
1
α
≥
расходится.
Условие
0
lim ( ) ( )
xa
x a fx C
α
→+
−=
может быть переформулировано так:
если при
0xa→+
имеет место эквивалентность
( )~
()
C
fx
xa
α
−
, где
0,C >
то при
01
α
<<
несобственный интеграл
()
b
a
f x dx
∫
сходится, а при
1
α
≥
расходится.
П
РИМЕР. Рассмотрим вопрос о сходимости несобственного интеграла
Глава 3
141
Несобственные интегралы
ç
è
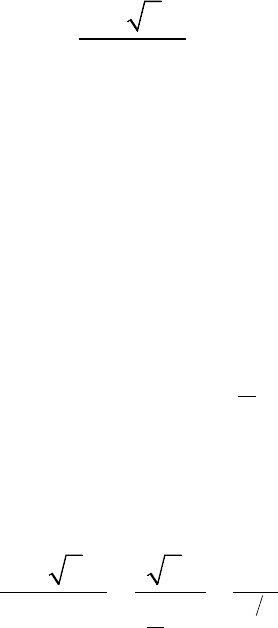
1
3
0
(sin )
1 cos
x
dx
x−
∫
.
Числитель и знаменатель подынтегральной функции непрерывны на про-
межутке
[0,1]
, причем знаменатель не обращается в ноль при
0x >
. Отсю-
да следует, что подынтегральная функция непрерывна на промежут-
ке
(0,1].
При
0x →
имеют место следующие эквивалентности:
2
1
sin ~ , 1 cos ~ .
2
xx x x−
Отсюда получаем, что при
0x →+
33
12
2
(sin ) ( ) 2
~
1
1 cos
2
xx
x
x
x
=
−
.
В силу следствия предыдущей теоремы, рассматриваемый интеграл схо-
дится.
Т
ЕОРЕМА 9 (КРИТЕРИЙ КОШИ СХОДИМОСТИ НЕСОБСТВЕННОГО ИНТЕГРА-
ЛА
). Предположим, что функция
f
определена на промежутке
(,]ab
и
интегрируема на отрезке
[ ,]ab
λ
+
для любого
λ
, удовлетворяющего усло-
вию
0 ba
λ
<<−
. Несобственный интеграл
()
b
a
f x dx
∫
сходится в том и
только том случае, когда выполняется следующее условие: по любому
0
ε
>
найдется такое
δ
,
0 ba
δ
<<−
, что для любых
1
λ
,
2
λ
, удовлетво-
ряющих условию
1
0
λδ
<<
,
2
0
λδ
<<
имеет место неравенство
Глава 3
142
Несобственные интегралы
ç
è
2
1
()
a
a
f x dx
λ
λ
ε
+
+
<
∫
.
С
ЛЕДСТВИЕ. Предположим, что функция
f
определена на проме-
жутке
(,]ab
и интегрируема на отрезке
[ ,]ab
λ
+
для любого
λ
, удовле-
творяющего условию
0 ba
λ
<<−
. Если сходится несобственный инте-
грал
| ( )|
b
a
f x dx
∫
, то сходится несобственный интеграл
()
b
a
f x dx
∫
и имеет
место оценка
() | ()|
bb
aa
f x dx f x dx≤
∫∫
.
О
ПРЕДЕЛЕНИЕ. Если сходится несобственный интеграл
| ( )|
b
a
f x dx
∫
,
то говорят, что
1) интеграл
()
b
a
f x dx
∫
сходится абсолютно;
2) функция
f
абсолютно интегрируема (в несобственном смысле) на
промежутке
[,]ab
.
Т
ЕОРЕМА 10. Предположим, что функции
f
и
g
определены на про-
межутке
[, )a +∞
и выполняются следующие условия:
1) для всех
[, )xa∈ +∞
| ()| ()fx gx≤
;
Глава 3
143
Несобственные интегралы
ç
è

2) сходится несобственный интеграл
()
a
g x dx
+∞
∫
;
3) для любого
λ
, удовлетворяющего условию
0 ba
λ
<<−
функция
f
интегрируема на отрезке
[ ,]ab
λ
+
.
Тогда функция
f
абсолютно интегрируема в несобственном смысле
на промежутке
[,]ab
и выполняется неравенство
() () .
bb
aa
f x dx g x dx≤
∫∫
Т
ЕОРЕМА 11 (ПРИЗНАК ДИРИХЛЕ). Предположим, что выполняются
следующие условия:
1) функция
f
непрерывна на промежутке
(,]ab
и имеет на этом
промежутке ограниченную первообразную;
2) функция
g
непрерывно дифференцируема и монотонна на про-
межутке
(,]ab
;
3)
0
lim ( ) 0
xa
gx
→+
=
.
Тогда несобственный интеграл
()()
b
a
f x g x dx
∫
сходится.
Т
ЕОРЕМА 12 (ПРИЗНАК АБЕЛЯ). Предположим, что выполняются сле-
дующие условия:
Глава 3
144
Несобственные интегралы
ç
è
1) функция
f
непрерывна на промежутке
(,]ab
и несобственный
интеграл
()
b
a
f x dx
∫
сходится;
2) функция
g
непрерывно дифференцируема, монотонна и ограниче-
на на промежутке
(,]ab
;
Тогда несобственный интеграл
()()
b
a
f x g x dx
∫
сходится.
З
АМЕЧАНИЕ. Мы рассмотрели случай, когда функция имеет особен-
ность на левом конце промежутка интегрирования. Аналогично рассмат-
ривается случай, когда функция имеет особенность на правом конце про-
межутка.
Глава 3
145
Несобственные интегралы
ç
è

Исторические сведения
Абель
Нильс Хенрик Абель (1802 – 1829)
Норвежский математик. Доказал теорему о неразрешимости уравнения
выше четвертой степени в радикалах. В математике используются терми-
ны «абелевы интегралы», «абелевы группы».
ç
è
Обратно

Д’Аламбер
Жан Лерон д’Аламбер (1717 – 1783)
Французский математик и философ. Сформулировал важный принцип ме-
ханики, названный его именем. Вместе с Д. Дидро редактировал знамени-
тую французскую «Энциклопедию».
Дополнения
147
Исторические сведения
ç
è
Обратно

Вейерштрасс
Карл Теодор Вильгельм Вейерштрасс (1815 – 1897)
Немецкий математик. Исследования Вейерштрасса посвящены математи-
ческому анализу, теории функций, вариационному исчислению, диффе-
ренциальной геометрии. В линейной алгебре разработал теорию элемен-
тарных делителей, используемую в теории матриц при нахождении мат-
рицы жордановой нормальной формы.
Дополнения
148
Исторические сведения
ç
è
Обратно

Дарбу
Жан Гастон Дарбý (1842–1917). Французский математик. Выполнил рабо-
ты по дифференциальной геометрии, теории интегрирования, алгебре, ме-
ханике.
Дополнения
149
Исторические сведения
ç
è
Обратно

Дирихле
Петер Густав Лежён Дирихле (1805 – 1859)
Немецкий математик. Создатель аналитической теории чисел. Выполнил
важные работы по теории функций.
Дополнения
150
Исторические сведения
ç
è
Обратно
