Пилиди В.С. лекции по высшей математике
Подождите немного. Документ загружается.


Из существования несобственного интеграла
0
()f x dx
+∞
∫
следует, что
первообразная
( ) ()
x
a
F x f t dt=
∫
,
xa≥
функции
f
является ограниченной.
Действительно, обозначим
0
() lim ().
M
K f x dx F x
+∞
→+∞
= =
∫
Тогда найдется та-
кое
Ma>
, что для всех
xM≥
выполняется неравенство
| () |1Fx K−<
, то
есть
1 () 1K Fx K−< < +
,
и функция
F
ограничена на промежутке
[, )M +∞
1
F
. Функция непрерыв-
на на промежутке
[, ]aM
. Из теоремы Вейерштрасса следует, что на этом
промежутке она ограничена. Окончательно получаем, что функция
F
ог-
раничена на промежутке
[, )a +∞
. Для применимости признака Дирихле к
функции
()(() )fx gx
α
−
на промежутке
[, )a +∞
остается заметить, что на
этом промежутке функция
()gx
α
−
непрерывна, монотонна и имеет место
равенство
lim ( ( ) ) 0
x
gx
α
→+∞
−=
.
Обращаясь к тождеству (∗) и учитывая, что функция
()fx
α
интегри-
руема на промежутке
[, )a +∞
, получаем требуемое утверждение.
П
РИМЕР. Покажем, что несобственный интеграл
0
sin x
dx
x
+∞
∫
сходится,
но не является абсолютно сходящимся.
1
Это свойство локальной ограниченности функции, рассмотренное нами ранее в случае
предела функции в конечной точке.
Глава 3
131
Несобственные интегралы
ç
è

ЗАМЕЧАНИЕ. При рассмотрении функции
sin x
x
всегда предполагает-
ся, что в точке
0x =
, являющейся точкой устранимого разрыва, функция
полагается равной единице. После этого данная функция становится не-
прерывной на всей вещественной оси.
В силу непрерывности функции
sin x
x
при
0x ≥
, она локально интег-
рируема на промежутке
[0, )+∞
. Для доказательства сходимости рассмат-
риваемого интеграла достаточно доказать, что сходится интеграл
sin x
dx
x
π
+∞
∫
.
Для этого воспользуемся признаком Дирихле. Полагаем:
1
() sin, () , .fx x gx x
x
π
= = ≥
Проверяем условия признака Дирихле.
1) функция
f
непрерывна на промежутке
[, )
π
+∞
и имеет на этом
промежутке ограниченную первообразную;
В проверке нуждается только утверждение о первообразной.
При
x
π
≥
имеет место равенство
sin ( cos ) cos 1.
x
x
tdt t x
π
π
=− =−−
∫
Отсюда для тех же
x
имеем:
Глава 3
132
Несобственные интегралы
ç
è
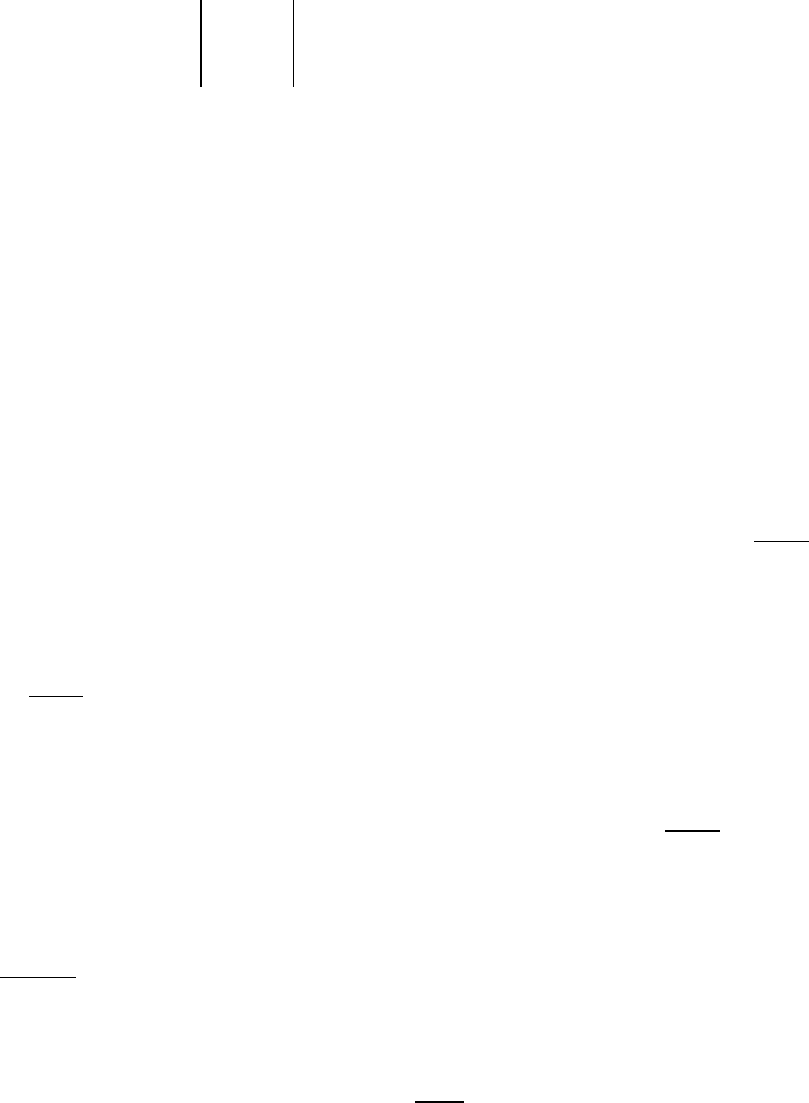
sin | cos 1| | cos | 1 2, .
x
tdt x x x
π
π
=− − ≤ +≤ ≥
∫
2) функция
g
непрерывно дифференцируема и монотонна на проме-
жутке
[, )
π
+∞
;
3)
lim ( ) 0
x
gx
→+∞
=
.
Эти свойства, очевидно, выполняются для рассматриваемой функ-
ции
g
.
В силу признака Дирихле, несобственный интеграл
sin x
dx
x
π
+∞
∫
схо-
дится. Тогда, как было отмечено выше, сходится несобственный интеграл
0
sin x
dx
x
+∞
∫
.
Покажем теперь, что несобственный интеграл
sin x
dx
x
π
+∞
∫
не сходится
абсолютно. Для этого достаточно показать, что первообразная функции
sin | |x
x
на промежутке
[, )
π
+∞
не является ограниченной. Обозначим:
sin
() ,
x
t
F x dt x
t
π
π
= ≥
∫
и покажем, что
()Fn
π
→ +∞
при
n → +∞
.
Действительно,
Глава 3
133
Несобственные интегралы
ç
è

( 1)
1
1
|sin | |sin |
() .
k
n
n
k
k
tt
F n dt dt
tt
π
π
ππ
π
+
−
=
= =
∑
∫∫
(∗)
Функция
1
()t
t
ϕ
=
монотонно убывает на промежутке
[, )
π
+∞
. Для
любого
[ , ( 1)]t kk
ππ
∈+
из оценки
( 1)tk
π
≤+
следует, что
11
( 1)tk
π
≥
+
. От-
сюда получаем:
( 1) ( 1)
|sin | 1
|sin |
( 1)
kk
kk
t
dt t dt
tk
ππ
ππ
π
++
≥=
+
∫∫
00
11
|sin( )| |sin |
( 1) ( 1)
k t dt t dt
kk
ππ
π
ππ
= += =
++
∫∫
0
0
11 2
sin ( cos ) .
( 1) ( 1) ( 1)
tdt t
kk k
π
π
ππ π
= = −=
++ +
∫
Учитывая полученную оценку, из (∗) находим:
11
11
2 21
() .
( 1) 1
nn
kk
Fn
kk
π
ππ
−−
= =
≥=
++
∑∑
Остается заметить, что сумма
1
1
1 11 1
123
n
k
kn
−
=
=++ +
+
∑
является частичной суммой расходящегося ряда
Глава 3
134
Несобственные интегралы
ç
è

1
1 11 1
123
k
kn
+∞
=
=++ ++
+
∑
с положительными членами и, следовательно,
1
1
1
lim
1
n
n
k
k
−
→+∞
=
= +∞
+
∑
. Поэтому
выполняется соотношение
lim ( )
n
Fn
π
→+∞
= +∞
, доказательство завершено.
В заключение остановимся еще на других случаях несобственных
интегралов по неограниченным промежуткам.
Предположим, что функция
f
определена на промежутке
( ,]a−∞
и
для любого
Ma<
интегрируема на промежутке
[ ,]Ma
. Если существует
предел
lim ( )
a
M
M
f x dx
→ −∞
∫
, то он обозначается через
()
a
f x dx
−∞
∫
и называется
несобственным интегралом от функции
f
по промежутку
( ,]a−∞
. В этом
случае говорят, что последний интеграл является сходящимся, а функ-
ция
f
называется интегрируемой (в несобственном смысле) по промежут-
ку
( ,]a−∞
. К таким интегралам с соответствующими изменениями приме-
нимы все утверждения, полученные для несобственных интегралов по
промежутку
[, )a +∞
. Если функция
f
определена на всей вещественной
оси и существуют несобственные интегралы
0
()f x dx
+∞
∫
и
0
()f x dx
−∞
∫
, то не-
собственный интеграл от функции
f
по всей вещественной оси определя-
ется равенством:
0
0
() () () .f x dx f x dx f x dx
+∞ +∞
−∞ −∞
= +
∫∫∫
Глава 3
135
Несобственные интегралы
ç
è

В этом случае говорят, что функция
f
интегрируема (в несобственном
смысле) по всей вещественной оси.
4. Интегралы от неограниченных функций
Предположим, что функция
f
интегрируема на отрезке
[,]ab
. В этом
случае выполняется равенство
0
lim () () .
bb
aa
f x dx f x dx
λ
λ
→+
+
=
∫∫
Действительно,
обозначим:
sup ( )
axb
M fx
≤≤
=
. Для числа
λ
, удовлетворяющего условию
0 ba
λ
<<−
, имеем:
() () () .
bba
aa a
f x dx f x dx f x dx
λ
λ
+
+
−=
∫∫ ∫
Отсюда следует, что
() () () | ()| 0
bb a a
aa a a
f x dx f x dx f x dx f x dx M
λλ
λ
λ
++
+
− = ≤ ≤ ⋅→
∫∫ ∫ ∫
при
0
λ
→+
.
Оказывается, что предел
0
lim ( )
b
a
f x dx
λ
λ
→+
+
∫
может существовать и для функ-
ции
f
, не являющейся ограниченной на промежутке
[,]ab
, и, следователь-
но, не являющейся интегрируемой на этом промежутке в обычном смысле.
Чтобы иметь возможность рассматривать такой предел, функция
f
долж-
Глава 3
136
Несобственные интегралы
ç
è

на быть определена и интегрируема на любом промежутке вида
[ ,]ab
λ
+
при произвольном значении
λ
, удовлетворяющем условию
0 ba
λ
<<−
.
Предположим, что функция
f
определена на промежутке
(,]ab
и
удовлетворяет следующим условиям:
1) эта функция является неограниченной на промежутке
(,]ab
;
2) при любом
λ
, удовлетворяющем условию
0 ba
λ
<<−
, функ-
ция
f
интегрируема на отрезке
[ ,]ab
λ
+
(и, следовательно, ограничена на
этом отрезке).
Если существует предел
0
lim ( )
b
a
f x dx
λ
λ
→+
+
∫
, то он обозначается че-
рез
()
b
a
f x dx
∫
и называется несобственным интегралом от функции
f
по
промежутку
[,]ab
. В этом случае говорят, что последний интеграл являет-
ся сходящимся, а функция
f
называется интегрируемой (в несобственном
смысле) по промежутку
[,]ab
.
З
АМЕЧАНИЕ. Условия 1) и 2) выполняются, например, если функ-
ция
f
определена и непрерывна на промежутке
(,]ab
. Тогда при любом
значении
λ
, удовлетворяющем условию
0 ba
λ
<<−
, эта функция непре-
рывна на отрезке
[ ,]ab
λ
+
и, следовательно, интегрируема на этом отрезке.
П
РИМЕР. Рассмотрим вопрос о сходимости несобственного интегра-
ла
1
0
dx
x
α
∫
,
0
α
>
.
Глава 3
137
Несобственные интегралы
ç
è
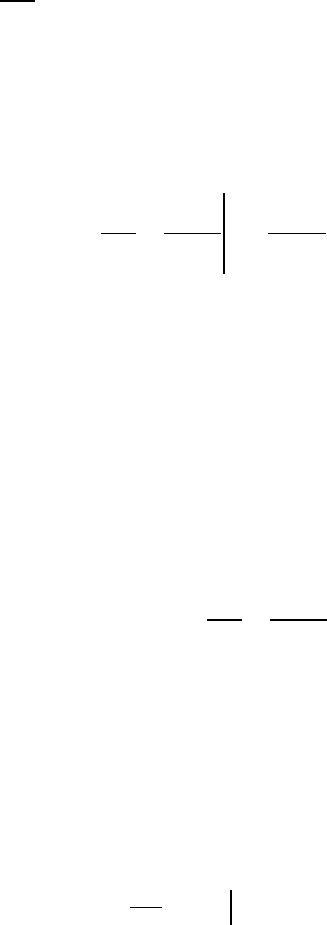
Функция
1
x
α
непрерывна на промежутке
(0,1]
и, следовательно, ин-
тегрируема на любом промежутке
[ ,1]
λ
,
01
λ
<<
. Предположим сначала,
что
1
α
≠
. Тогда
1
1
1
1
1
( 1).
11
dx x
x
α
α
α
λ
λ
λ
αα
−
−
= = −
−−
∫
При
0
λ
→+
величина
1
1
α
λ
−
−
имеет (конечный) предел в том и только том
случае, когда
10
α
−>
, то есть
1
α
<
. При этом
1
0
lim ( 1) 1
α
λ
λ
−
→+
−=
. Итак, при
01
α
<<
рассматриваемый несобственный интеграл сходится, и имеет ме-
сто равенство
1
0
1
1
dx
x
α
α
=
−
∫
.
При
1
α
>
указанный несобственный интеграл расходится.
Если
1
α
=
, то для любого
0
λ
>
1
1
ln ln
dx
x
x
λ
λ
λ
= = − → +∞
∫
при
0
λ
→+
. Следовательно, несобственный интеграл в этом случае расхо-
дится. Окончательно получаем, что несобственный интеграл сходится при
1
α
<
и расходится при
1
α
≥
.
Аналогично находим, что несобственный интеграл
Глава 3
138
Несобственные интегралы
ç
è

()
b
a
dx
xa
α
−
∫
,
ab−∞ < < < +∞
,
0
α
>
сходится при
01
α
<<
и расходится при
1
α
≥
.
Приведенный в предыдущем примере подход может быть обобщен
следующим образом.
Предположим, что функция
f
определена и непрерывна на проме-
жутке
(,]ab
. Обозначим через
F
произвольную первообразную функ-
ции
f
на этом промежутке Выберем произвольное число
λ
, удовлетво-
ряющее условию
0 ba
λ
<<−
Применим формулу Ньютона-Лейбница к
функции
f
на промежутке
[ ,]ab
λ
+
:
( ) ( ) ( ).
b
a
fxdxFb Fa
λ
λ
+
= −+
∫
Отсюда следует, что предел
0
lim ( )
b
a
f x dx
λ
λ
→+
+
∫
существует в том и только том
случае, когда существует предел
0
lim ( )Fa
λ
λ
→+
+
, и при выполнении этих ус-
ловий имеет место равенство:
0
( ) ( ) lim ( ).
b
a
fxdxFb Fa
λ
λ
→+
=−+
∫
Обозначая, как обычно,
0
lim ( ) ( 0)Fa Fa
λ
λ
→+
+= +
, последнюю формулу пе-
репишем так:
Глава 3
139
Несобственные интегралы
ç
è

( ) ( ) ( 0),
b
a
fxdxFb Fa= −+
∫
или
0
() ()
b
b
a
a
f x dx F x
+
=
∫
. Мы получили формулу Ньютона-Лейбница для
случая неограниченной функции.
Для рассматриваемого случая остаются в силе все приведенные вы-
ше свойства несобственных интегралов по неограниченному промежутку.
Их доказательства несущественно отличаются от предыдущего случая. По-
этому мы остановимся лишь на формулировках основных результатов.
Т
ЕОРЕМА 7 (ПРИЗНАК СРАВНЕНИЯ ДЛЯ НЕСОБСТВЕННЫХ ИНТЕГРАЛОВ).
Предположим, что функции
f
и
g
определены на промежутке
(,]ab
и
интегрируемы на отрезке
[ ,]ab
λ
+
для любого
λ
, удовлетворяющего ус-
ловию
0 ba
λ
<<−
. Допустим, что обе эти функции принимают только
неотрицательные значения, и для любого
(,]x ab∈
выполняется неравен-
ство
() ()fx gx≤
. Тогда:
1) если несобственный интеграл
()
b
a
g x dx
∫
сходится, то несобствен-
ный интеграл
()
b
a
f x dx
∫
также сходится;
2) если несобственный интеграл
()
b
a
f x dx
∫
расходится, то несобст-
венный интеграл
()
b
a
g x dx
∫
расходится.
Глава 3
140
Несобственные интегралы
ç
è
