Пилиди В.С. лекции по высшей математике
Подождите немного. Документ загружается.


Мы доказали ее в предположении, что
1n >
. Очевидно, что она оста-
ется верной и при
1n =
. Сформулируем окончательный результат.
Т
ЕОРЕМА 11. Предположим, что
n∈
,
1
{}
n
kk
a
=
— монотонная чи-
словая последовательность,
1
{}
n
kk
b
=
— произвольная числовая последова-
тельность. Тогда имеет место оценка
1
1
11
(| | 2| |) max .
nk
kk n i
kn
ki
ab a a b
≤≤
= =
≤+ ⋅
∑∑
З
АМЕЧАНИЕ. Приведенное в теореме неравенство называется нера-
венством Абеля.
Неравенство Абеля позволяет доказать следующие признаки сходи-
мости рядов.
Т
ЕОРЕМА 12 (ПРИЗНАК ДИРИХЛЕ). Предположим, что последователь-
ность
1
{}
nn
a
+∞
=
монотонная и сходится к нулю, а последовательность час-
тичных сумм ряда
1
n
n
b
+∞
=
∑
ограничена. Тогда ряд
1
nn
n
ab
+∞
=
∑
сходится.
Д
ОКАЗАТЕЛЬСТВО. Обозначим:
1
sup
n
k
n
k
cb
∈
=
=
∑
. Выберем произвольное
0
ε
>
и найдем такое
N
, чтобы для всех
nN≥
выполнялось неравенство
||
n
a
ε
<
. Выберем произвольные
nN≥
и
1p =
, 2, … . Применяя неравен-
ство Абеля к последовательностям
1
{}
np
k
kn
a
+
= +
и
1
{}
np
k
kn
b
+
= +
, получаем:
1
1
11
(| | 2| |) max 3 .
np nq
kk n np k
qp
kn kn
ab a a b c
ε
++
++
≤≤
=+=+
≤+ ⋅ ≤
∑∑
Глава 2
101
Числовые ряды
ç
è

В силу произвольности
ε
, из критерия Коши сходимости ряда выво-
дим сходимость ряда
1
nn
n
ab
+∞
=
∑
.
Теорема доказана.
З
АМЕЧАНИЕ. Признак Лейбница является следствием признака Ди-
рихле. Действительно, предположим, что последовательность
1
{}
nn
a
+∞
=
по-
ложительных чисел монотонно сходится к нулю. Рассмотрим последова-
тельность
1
( 1)
n
n
b
−
= −
,
n∈
. Частичные суммы ряда
1
n
n
b
+∞
=
∑
принимают по-
следовательно значения
1
и
0
, следовательно, они образуют ограниченную
последовательность. В силу признака Дирихле, ряд
11
( 1)
n
nn n
nn
ab a
+∞ +∞
= =
= −
∑∑
сходится.
Т
ЕОРЕМА 13 (ПРИЗНАК АБЕЛЯ). Предположим, что последователь-
ность
1
{}
nn
a
+∞
=
монотонная и ограниченная, а ряд
1
n
n
b
+∞
=
∑
сходится. Тогда ряд
1
nn
n
ab
+∞
=
∑
сходится.
Д
ОКАЗАТЕЛЬСТВО. Обозначим:
sup| |
n
n
ca
∈
=
. Выберем произвольное
0
ε
>
. В силу сходимости ряда
1
n
n
b
+∞
=
∑
, из критерия Коши получаем, что су-
ществует такое
N
, что для всех
nN≥
и
1p =
, 2, … выполняется неравен-
ство
1
np
k
kn
b
ε
+
= +
<
∑
. Зафиксируем числа
n
и
p
, удовлетворяющие указанным
Глава 2
102
Числовые ряды
ç
è

условиям. Применяя неравенство Абеля к последовательностям
1
{}
np
k
kn
a
+
= +
и
1
{}
np
k
kn
b
+
= +
, получаем:
1
1
11
(| | 2| |) max 3 .
np nq
kk n np k
qp
kn kn
ab a a b c
ε
++
++
≤≤
=+=+
≤+ ⋅ ≤
∑∑
В силу произвольности
ε
, из критерия Коши сходимости ряда выво-
дим сходимость ряда
1
nn
n
ab
+∞
=
∑
.
Теорема доказана.
З
АМЕЧАНИЕ 1. Признак Абеля может быть переформулирован сле-
дующим образом: если члены сходящегося числового ряда умножить на
соответствующие элементы ограниченной монотонной последовательно-
сти, то полученный ряд будет сходиться.
З
АМЕЧАНИЕ 2. Признак Абеля, как и признак Лейбница, может быть
выведен из признака Дирихле. Действительно, предположим, что последо-
вательность
1
{}
nn
a
+∞
=
монотонная и ограниченная, а ряд
1
n
n
b
+∞
=
∑
сходится. По-
следовательность
1
{}
nn
a
+∞
=
является сходящейся. Обозначим:
lim .
n
n
aa
→+∞
=
Воспользуемся равенством
() , .
nn n n n
a b a a b ab n=−+ ∈
(∗)
Учтем, что
lim ( ) 0
n
n
aa
→+∞
−=
, а последовательность частичных сумм ряда
1
n
n
b
+∞
=
∑
является сходящейся и, следовательно, ограниченной. Поэтому чи-
Глава 2
103
Числовые ряды
ç
è

словой ряд
1
()
nn
n
a ab
+∞
=
−
∑
сходится по признаку Дирихле. И сходимости ря-
да
1
n
n
b
+∞
=
∑
вытекает сходимость ряда
1
n
n
ab
+∞
=
∑
. Теперь из равенства (∗) выво-
дим сходимость ряда
1
nn
n
ab
+∞
=
∑
.
П
РИМЕР. Рассмотрим ряд
1
1
arctg
( 1)
n
n
n
n
+∞
−
=
−
∑
. Применяем признак Абе-
ля. Ряд
1
1
( 1)
n
n
n
−
+∞
=
−
∑
сходится по признаку Лейбница, последовательность
1
{arctg }
n
n
+∞
=
монотонно возрастает и ограничена сверху числом
2
π
. Следо-
вательно, рассматриваемый ряд сходится.
З
АМЕЧАНИЕ. Можно показать, что последовательность
1
arctg
n
n
n
+∞
=
является монотонной (и, разумеется, сходится к нулю). Отсюда, в силу
признака Лейбница, вытекает сходимость рассмотренного выше ряда. Од-
нако такой вариант решения является несколько более сложным, чем при-
веденный выше.
Глава 2
104
Числовые ряды
ç
è
Глава 3. Несобственные интегралы
При рассмотрении определенных интегралов мы рассматривали
функции, определенные на отрезке, и необходимым условием существова-
ния определенного интеграла была ограниченность функции. В этом раз-
деле будет рассмотрено расширение понятия определенного интеграла на
случай неограниченной области определения и неограниченной функции.
1. Определение несобственного интеграла
Предположим, что функция
f
определена на промежутке
[, )a +∞
и
при любом
Ma>
интегрируема на отрезке
[, ]aM
. Если существует пре-
дел
lim ( )
M
M
a
f x dx
→+∞
∫
, то он обозначается через
()
a
f x dx
+∞
∫
и называется не-
собственным интегралом от функции
f
по промежутку
[, )a +∞
. В этом
случае говорят, что последний интеграл является сходящимся, а функ-
ция
f
называется интегрируемой (в несобственном смысле) по промежут-
ку
[, )a +∞
.
О
ПРЕДЕЛЕНИЕ. Если функция
f
определена на промежутке
[, )a +∞
и
при любом
Ma>
интегрируема на отрезке
[, ]aM
, будем говорить, что эта
функция локально интегрируема на промежутке
[, )a +∞
.
ç
è
Отметим, в частности, что если функция
f
непрерывна на проме-
жутке
[, )a +∞
, то она локально интегрируема на этом промежутке. Дейст-
вительно, для любого
Ma>
функция
f
непрерывна на отрезке
[, ]aM
(точнее говоря, сужение этой функции является непрерывным на этом от-
резке) и, следовательно, интегрируема на этом отрезке.
З
АМЕЧАНИЕ. Имеются многочисленные аналогии между утвержде-
ниями, касающимися сходимости числовых рядов, и сходимости несобст-
венных интегралов рассматриваемого вида. Отметим, одно утверждение из
теории рядов, которое не имеет точного аналога для несобственных инте-
гралов. Напомним, что если числовой ряд
1
n
n
a
+∞
=
∑
сходится, то выполняется
соотношение
lim 0
n
n
a
→+∞
=
. В случае несобственных интегралов из сходимо-
сти интеграла
()
a
f x dx
+∞
∫
не следует с необходимостью, что
lim ( ) 0.
x
fx
→+∞
=
Например, можно доказать, что сходится несобственный интеграл
2
0
sin x dx
+∞
∫
, однако при
x → +∞
подынтегральная функция не стремится к
нулю. Более того, в случае сходимости интеграла
()
a
f x dx
+∞
∫
функция
f
может даже оказаться неограниченной на промежутке
[, )a +∞
(хотя при
любом
Ma>
она является ограниченной на промежутке
[, ]aM
, поскольку
она интегрируема на этом промежутке).
У
ПРАЖНЕНИЕ. Доказать, что если несобственный интеграл
()
a
f x dx
+∞
∫
сходится, то для любого
0h >
имеет место следующее равенство:
Глава 3
106
Несобственные интегралы
ç
è
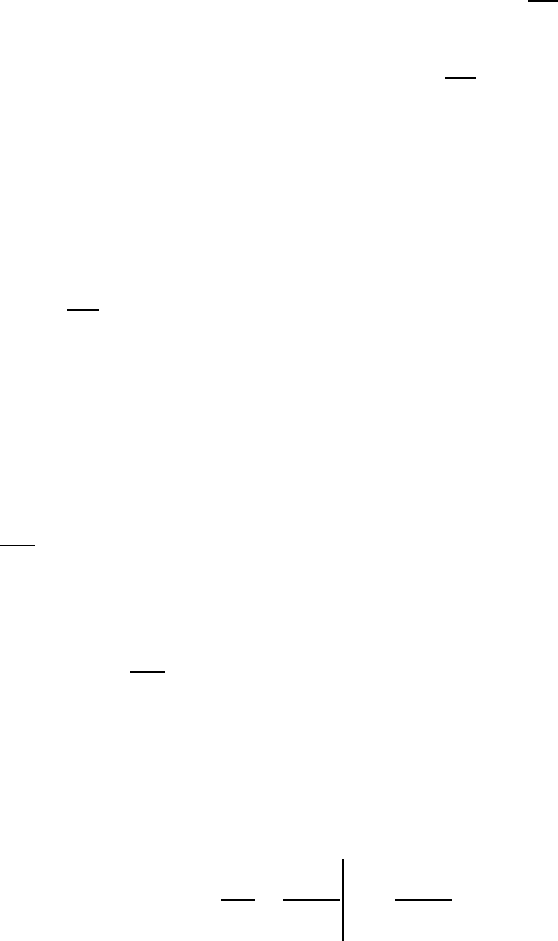
lim ( )
Mh
M
M
f x dx
+
→+∞
∫
.
У
ПРАЖНЕНИЕ. Рассмотрим функцию
f
, задаваемую на промежутке
[1, )+∞
условием
3
3
1
,если ,
()
1
0,если 1.
n nxn
n
fx
n xn
n
≤≤+
=
+ <<+
для
1n =
, 2,… . Доказать, что несобственный интеграл
1
()f x dx
+∞
∫
сходится
и равен
2
1
1
n
n
+∞
=
∑
. Обратите внимание, что подынтегральная функция является
неограниченной на промежутке
[1, )+∞
.
П
РИМЕР. Проанализируем сходимость несобственного интегра-
ла
1
dx
x
α
+∞
∫
.
Функция
1
x
α
непрерывна на промежутке
[1, )+∞
и, следовательно,
локально интегрируема на этом отрезке. Предположим сначала, что
1.
α
≠
Тогда
1
1
1
1
1
(1 )
11
M
M
dx x
M
x
α
α
α
αα
−
−
= = −
−−
∫
.
Глава 3
107
Несобственные интегралы
ç
è
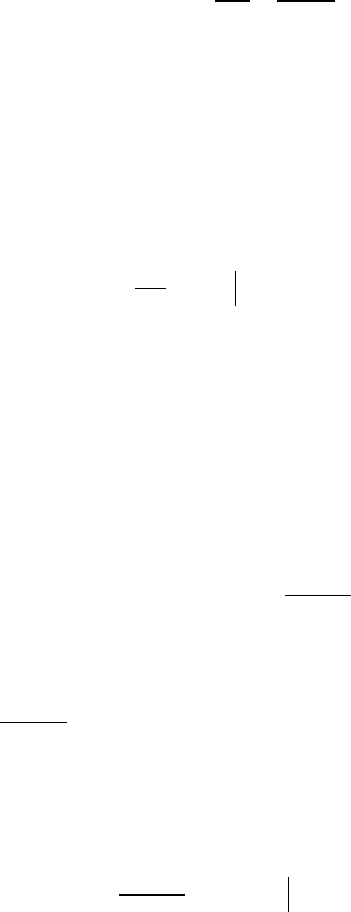
При
M
→ +∞
величина
1
1 M
α
−
−
имеет (конечный) предел в том и только
том случае, когда
1
α
>
. При этом
1
lim (1 ) 1
M
M
α
−
→+∞
−=
. Итак, при
1
α
>
рас-
сматриваемый несобственный интеграл сходится, и имеет место равенство
1
1
1
dx
x
α
α
+∞
=
−
∫
.
При
1
α
<
указанный несобственный интеграл расходится.
Остается проанализировать случай
1
α
=
. В этом случае
1
1
ln ln
M
M
dx
xM
x
= = → +∞
∫
при
M → +∞
. Следовательно, несобственный интеграл в этом случае рас-
ходится. Окончательно получаем, что несобственный интеграл сходится
при
1
α
>
и расходится при
1
α
≤
.
П
РИМЕР. Рассмотрим интеграл
2
0
1
dx
x
+∞
+
∫
.
Функция
2
1
1x +
непрерывна на промежутке
[0, )+∞
и, следовательно,
локально интегрируема на нем. Далее,
2
0
0
arctg arctg .
1
M
M
dx
xM
x
= =
+
∫
Глава 3
108
Несобственные интегралы
ç
è

Остается заметить, что
lim arctg
2
M
M
π
→+∞
=
и, следовательно, рассматривае-
мый несобственный интеграл сходится и
2
0
2
1
dx
x
π
+∞
=
+
∫
.
Приведенные примеры являются частным случаем следующего об-
щего подхода.
Предположим, что функция
f
определена и непрерывна на проме-
жутке
[, )a +∞
. Обозначим через
F
произвольную первообразную функ-
ции
f
на промежутке
[, )a +∞
.
1
( ) ( ) ( ).
M
a
fxdxFM Fa= −
∫
Применяя формулу Ньютона-Лейбница,
получаем:
Отсюда следует, что предел
lim ( )
M
M
a
f x dx
→+∞
∫
существует в том и только том
случае, когда существует предел
lim ( )
M
FM
→+∞
, и при выполнении этих ус-
ловий имеет место равенство:
( ) lim ( ) ( ).
M
a
fxdx FM Fa
+∞
→+∞
= −
∫
Обозначая
lim ( ) ( )
M
FM F
→+∞
= +∞
, последнюю формулу перепишем так:
1
Такой первообразной является, например, функция
( ) ()
x
a
F x f t dt=
∫
,
ax≤ < +∞
.
Глава 3
109
Несобственные интегралы
ç
è

( ) ( ) ( ),
a
fxdxF Fa
+∞
= +∞ −
∫
или
() ()
a
a
f x dx F x
+∞
+∞
=
∫
. Мы получили формулу Ньютона-Лейбница для
неограниченного промежутка.
Отметим теперь некоторые свойства несобственных интегралов.
1°. Предположим, что сходится несобственный интеграл
() .
a
f x dx
+∞
∫
Тогда для любого
ba>
сходится несобственный интеграл
()
b
f x dx
+∞
∫
и
имеет место равенство
() () () .
b
aab
f x dx f x dx f x dx
+∞ +∞
= +
∫∫∫
Действительно, для
Mb>
, имеет место следующее соотношение:
() () () ,
MbM
aab
f x dx f x dx f x dx= +
∫∫∫
откуда следует, что
() () () .
MMb
b aa
f x dx f x dx f x dx= −
∫∫∫
Глава 3
110
Несобственные интегралы
ç
è
