Пилиди В.С. лекции по высшей математике

Подождите немного. Документ загружается.

В силу этого соотношения, из существования предела

lim ( )

f x dx

→+∞

∫

вы-

текает существование предела

lim ( )

f x dx

→+∞

∫

и равенство

() () () ,

b aa

f x dx f x dx f x dx

+∞ +∞

= −

∫ ∫∫

равносильное доказываемому соотношению.

2°. Предположим, что функция

определена и локально интегриру-

ема на промежутке

[, )a +∞

. Если для некоторого

ba>

сходится несобст-

венный интеграл

()

f x dx

+∞

∫

, то сходится и несобственный инте-

грал

()

f x dx

+∞

∫

Доказательство аналогично предыдущему случаю, и мы его опуска-

ем.

АМЕЧАНИЕ. Обращаем внимание читателя на некоторые изменения в

формулировках. В случае свойства 1° не требовалось локальной интегри-

руемости функций: если говорится о сходимости несобственного интегра-

ла

()

f x dx

+∞

∫

, то по определению функция

должна быть локально интег-

рируема на промежутке

[, )a +∞

. В случае свойства 2° из сходимости несоб-

ственного интеграла

()

f x dx

+∞

∫

следует, что функция

локально интегри-

Глава 3

111

Несобственные интегралы

руема на промежутке

[, )b +∞

. Условие локальной интегрируемости этой

функции на промежутке

[, )a +∞

гарантирует ее интегрируемость на отрез-

ке

[,]ab

3°. Если сходятся несобственные интегралы

()

f x dx

+∞

∫

()

g x dx

+∞

∫

то для любых

∈

сходится несобственный интеграл

( () ())

f x g x dx

αβ

+∞

∫

и имеет место равенство

( () ()) () () .

a aa

f x g x dx f x dx g x dx

αβ α β

+∞ +∞ +∞

+= +

∫ ∫∫

Действительно, для любого

Ma>

функции

интегрируемы на

отрезке

[, ]aM

. Тогда на этом отрезке интегрируема функция

αβ

имеет место следующее равенство:

( () ()) () () .

M MM

a aa

f x g x dx f x dx g x dx

αβ α β

+= +

∫ ∫∫

Переходя к пределу при

M → +∞

, получаем, что интеграл

( () ())

f x g x dx

αβ

+∞

∫

сходится, и имеет место требуемое соотношение.

Отметим также следующее простое утверждение.

Глава 3

112

Несобственные интегралы

4°. Если для всех

[, )xa∈ +∞

выполняется неравенство

() ()fx gx≤

несобственные интегралы

()

f x dx

+∞

∫

()

g x dx

+∞

∫

сходятся, то

() () .

f x dx g x dx

+∞ +∞

≤

∫∫

2. Несобственные интегралы от неотрицательных функций

Перейдем к рассмотрению частного случая неотрицательных подын-

тегральных функций.

Нам потребуется следующее утверждение, являющееся точным ана-

логом критерия сходимости возрастающих последовательностей.

ЕММА. Для функции

, определенной и возрастающей на проме-

жутке

[, )a +∞

, следующие условия равносильны:

1) существует предел

lim ( )

→+∞

;

2) функция

является ограниченной на промежутке

[, )a +∞

ОКАЗАТЕЛЬСТВО. 1)⇒2). Допустим, что

lim ( )

fx A

→+∞

. Выберем

произвольную точку

[, )xa∈ +∞

. В силу возрастания функции

, для лю-

бого значения

xx≥

выполняется неравенство

( ) ()fx fx≤

. Переходя

здесь к пределу при

x → +∞

, находим, что

()fx A≤

. В силу произвольно-

сти точки

, функция

ограничена на рассматриваемом промежутке.

Глава 3

113

Несобственные интегралы

2)⇒1). Обозначим

sup{ ( ): }A fx a x= ≤ < +∞

. Выберем произвольное

. По определению точной верхней грани, найдется такое значение

[, )xa∈ +∞

, что

()fx A

>−

. Тогда для любого

xx≥

имеем:

() ( )fx fx A

≥ >−

то есть для этого значения

выполняется соотношение

() .A fx A

−< ≤

Отсюда следует, что

| () |fx A

−<

. В силу произвольности

, это означает,

что

lim ( )

fx A

→+∞

Лемма доказана.

Перейдем к анализу сходимости несобственных интегралов. Предпо-

ложим, что функция

определена, локально интегрируема на промежутке

[, )a +∞

и всюду принимает неотрицательные значения. Тогда функция

( ) ()

F M f x dx=

∫

Ma≥

является возрастающей. В силу леммы, сущест-

вование предела

lim ( )

→+∞

равносильно ограниченности функции

на

промежутке

[, )a +∞

. Это утверждение позволяет доказать признаки срав-

нения, аналогичные признакам сравнения для знакопостоянных рядов.

ЕОРЕМА 1 (ПРИЗНАК СРАВНЕНИЯ ДЛЯ НЕСОБСТВЕННЫХ ИНТЕГРАЛОВ).

Предположим, что функции

определены и локально интегрируемы

на промежутке

[, )a +∞

. Допустим, что обе эти функции принимают

только неотрицательные значения, и для любого

[, )xa∈ +∞

выполняется

неравенство

() ()fx gx≤

. Тогда:

Глава 3

114

Несобственные интегралы

1) если несобственный интеграл

()

g x dx

+∞

∫

сходится, то несобст-

венный интеграл

()

f x dx

+∞

∫

также сходится;

2) если несобственный интеграл

()

f x dx

+∞

∫

расходится, то несобст-

венный интеграл

()

g x dx

+∞

∫

также расходится.

ОКАЗАТЕЛЬСТВО. Обозначим:

( ) () , ( ) () , .

F M f x dx G M g x dx M a= = ≥

∫∫

Из условия теоремы следует, что для любого

Ma≥

выполняется неравен-

ство

() ()FM GM≤

. Если несобственный интеграл

()

g x dx

+∞

∫

сходится, то

функция

ограничена на промежутке

[, )a +∞

. Тогда на этом промежутке

ограничена и функция

. Следовательно, несобственный интеграл

()

f x dx

+∞

∫

сходится. Мы доказали свойство 1). Свойство 2) является логи-

чески равносильным свойству 1)

Теорема доказана.

АМЕЧАНИЕ. Выше было отмечено, что сходимость несобственного

интеграла

()

f x dx

+∞

∫

равносильна сходимости несобственного интеграла

Глава 3

115

Несобственные интегралы

()

f x dx

+∞

∫

для некоторого (а тогда и для любого)

ba>

. Поэтому утвержде-

ние теоремы остается в силе, если функции

принимают неотрица-

тельные значения, начиная с некоторого места (то есть для всех

xc≥

при

некотором

ca>

) и, если неравенство

() ()fx gx≤

также выполняется, на-

чиная с некоторого места. При выполнении этих условий мы будем ссы-

латься на предыдущую теорему без особых оговорок.

Дадим теперь признак сравнения для несобственных интегралов в

предельной форме.

ЕОРЕМА 2. Предположим, что функции

определены на про-

межутке

[, )a +∞

, принимают на этом промежутке положительные зна-

чения и существует конечный предел

()

lim 0

()

→+∞

. Тогда несобственные

интегралы

()

f x dx

+∞

∫

()

g x dx

+∞

∫

сходятся или расходятся одновременно.

ОКАЗАТЕЛЬСТВО. Обозначим

()

lim

()

→+∞

. Существует такое

что для всех

xN≥

выполняется неравенство

()

≤+

. Тогда для этих

значений

получаем:

() ( 1)()fx A gx≤+

. Из этого неравенства и сходимо-

сти интеграла

( 1) ( )

A g x dx

+∞

∫

, в силу предыдущей теоремы, вытекает схо-

димость интеграла

()

f x dx

+∞

∫

Глава 3

116

Несобственные интегралы

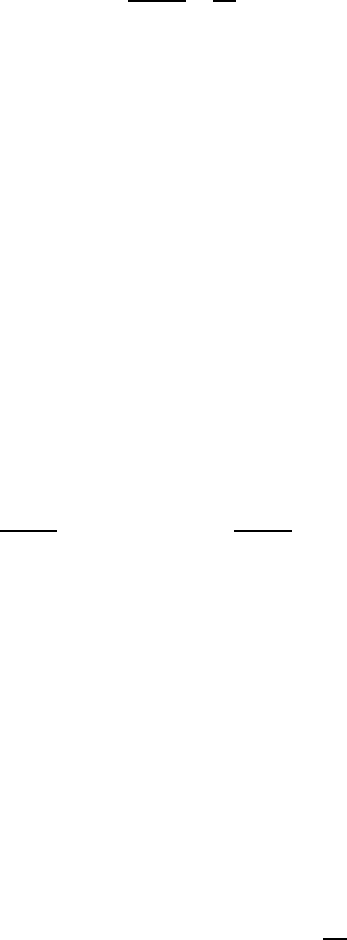
Из доказанного и соотношения

() 1

lim

()

fx A

→+∞

следует, что сходи-

мость интеграла

()

f x dx

+∞

∫

влечет сходимость интеграла

()

g x dx

+∞

∫

Теорема доказана.

АМЕЧАНИЕ 1. Разумеется, теорема остается в силе, если неравенства

() 0fx>

() 0gx>

выполняются для всех достаточно больших значений

АМЕЧАНИЕ 2. Как и в случае признака сравнения в предельной фор-

ме для знакопостоянных рядов, утверждение теоремы может быть уточне-

но, если допустить случаи

()

lim 0

()

→+∞

или

()

lim

()

→+∞

= +∞

. В первом

случае из сходимости интеграла

()

g x dx

+∞

∫

следует сходимость интеграла

()

f x dx

+∞

∫

(обращаем внимание читателя, что в первой части доказательст-

ва теоремы условие

0A >

не используется). Более того, в этом случае дос-

таточно предполагать, что функция

принимает, начиная с некоторого

места неотрицательные значения, поскольку отношение

рассматри-

ваться не будет. Во втором случае из сходимости интеграла

()

f x dx

+∞

∫

сле-

дует сходимость интеграла

()

g x dx

+∞

∫

. Детальный анализ этих случаев пре-

доставляется читателю.

Глава 3

117

Несобственные интегралы

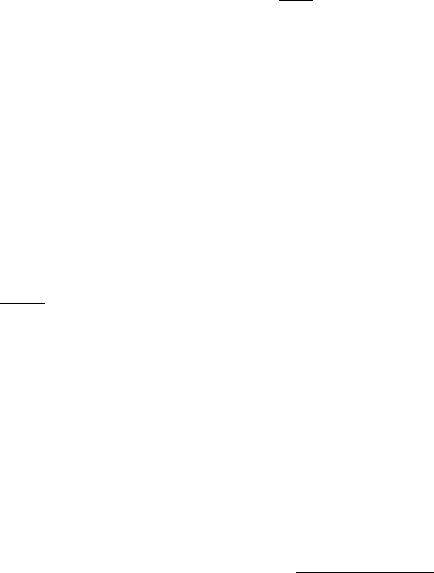
СЛЕДСТВИЕ ТЕОРЕМЫ. Предположим, что функция

определена и

локально интегрируема на промежутке

[, )a +∞

, принимает на этом про-

межутке положительные значения и для некоторого

выполняется

равенство

lim ( )

xfx C

→+∞

, где

0C >

. Тогда при

несобственный ин-

теграл

()

f x dx

+∞

∫

сходится, а при

≤

расходится.

Это утверждение вытекает из полученных выше условий сходимости

несобственного интеграла

+∞

∫

. Напомним, что этот интеграл сходится

при

и расходится при

≤

Условие

lim ( )

xfx C

→+∞

может быть переформулировано в сле-

дующих терминах: если при

x → +∞

имеет место эквивалентность

~()

, где

0C >

, то при

несобственный интеграл

()

f x dx

+∞

∫

сходится, а при

≤

расходится.

РИМЕР. Докажем сходимость несобственного интеграла

2 34

+∞

−−

∫

В силу равенства

4 2 22

2 1 ( 1)xx x+ += +

, знаменатель дроби при

0x ≥

является положительным. Отсюда следует, что подынтегральная функция

определена и непрерывна при

0x ≥

. Поскольку

2 34xx− − → +∞

при

x → +∞

, числитель дроби, а, значит, и подынтегральная функция, начиная

с некоторого места становятся положительными. Из сказанного следует,

Глава 3

118

Несобственные интегралы

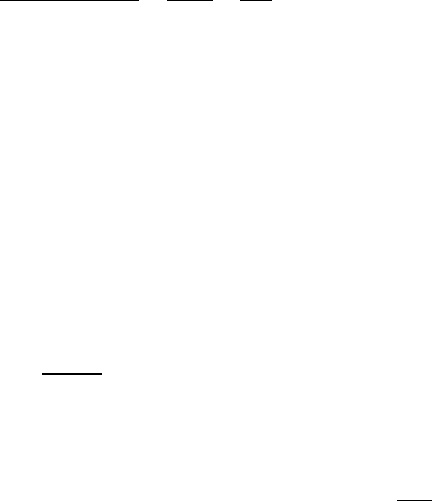
что подынтегральная функция определена и непрерывна при

0x ≥

и поло-

жительна, начиная с некоторого места. Учитывая, что при

x → +∞

имеют

место эквивалентности

2 24 2 4

2 3 42, 2~ 1~ ,x x xx x x−− + +

для подынтегральной функции при

x → +∞

получаем:

42 42

2 3 42 2

xx x

xx xx

−−

В силу приведенного выше следствия теоремы, интеграл является сходя-

щимся.

ПРАЖНЕНИЕ. Проанализировать сходимость несобственного инте-

грала

+∞

∫

∈

КАЗАНИЕ. При

≠

не существует функции вида

, эквивалент-

ной подынтегральной функции при

x → +∞

. Для анализа сходимости при

≠

можно воспользоваться следующей оценкой: для любого

суще-

ствует такая константа

()CC

, что для всех

1x ≥

имеет место неравенст-

во

ln x Cx

≤

. В случае

можно найти первообразную подынтеграль-

ной функции и с ее помощью решить вопрос о сходимости.

Глава 3

119

Несобственные интегралы

3. Признаки сходимости несобственного интеграла в общем

случае

Прежде всего, приведем общий критерий сходимости несобственно-

го интеграла.

ЕОРЕМА 3 (КРИТЕРИЙ КОШИ СХОДИМОСТИ НЕСОБСТВЕННОГО ИНТЕГРА-

ЛА

). Предположим, что функция

определена и локально интегрируема

на промежутке

[, )a +∞

. Несобственный интеграл

()

f x dx

+∞

∫

сходится в

том и только том случае, когда выполняется следующее условие: по лю-

бому

найдется такое

Na>

, что для любых

MN≥

выполня-

ется неравенство

()

f x dx

∫

ОКАЗАТЕЛЬСТВО. Сходимость несобственного интеграла

()

f x dx

+∞

∫

по определению равносильна существованию предела функции

( ) ()

F M f x dx=

∫

при

M → +∞

. Воспользуемся критерием Коши существования предела

функции при

M → +∞

. Согласно этому критерию, предел

lim ( )

→+∞

су-

ществует в том и только том случае, когда по любому

найдется такое

, что для любых

MN≥

выполняется неравенство

| ( ) ( )|FM FM

−<

Глава 3

120

Несобственные интегралы