Пилиди В.С. лекции по высшей математике
Подождите немного. Документ загружается.


Учитывая произвольность числа
ε
, из критерия интегрируемости выво-
дим, что функция
f
является интегрируемой.
Теорема доказана.
С
ЛЕДСТВИЕ. Предположим, что функция
f
определена на отрез-
ке
[,]ab
, непрерывна во всех точках интервала
(,)ab
и имеет односто-
ронние пределы в концах отрезка
[,]ab
. Тогда функция
f
интегрируема на
отрезке
[,]ab
.
Д
ОКАЗАТЕЛЬСТВО. Определим функцию
g
на отрезке
[,]ab
условия-
ми:
() ()gx fx=
, если
axb<<
,
0
( ) lim ( )
xa
ga f x
→+
=
,
0
( ) lim ( )
xb
gb f x
→−
=
. Тогда
функция
g
непрерывна на отрезке
[,]ab
. Действительно, во всех внутрен-
них точках этого отрезка она непрерывна, в силу непрерывности функ-
ции
f
. Из соотношения
00
( ) lim ( ) lim ( ),
xa xa
ga f x gx
→+ →+
= =
следует непрерыв-
ность слева функции
g
в точке
a
. Аналогично получаем ее непрерывность
справа в точке
b
. По доказанной теореме функция
g
интегрируема на от-
резке
[,]ab
. Остается заметить, что значения функций
f
и
g
могут отли-
чаться не более, чем в двух точках. В силу теоремы 2, функция
f
интегри-
руема на отрезке
[,]ab
.
Следствие доказано.
П
РИМЕР. Рассмотрим на произвольном отрезке
[,]ab
функцию
()fx x=
. Эта функция непрерывна на указанном отрезке и, следовательно,
интегрируема на нем. Покажем, что
22
2
b
a
ba
xdx
−
=
∫
.
Глава 1
31
Определенный интеграл
ç
è
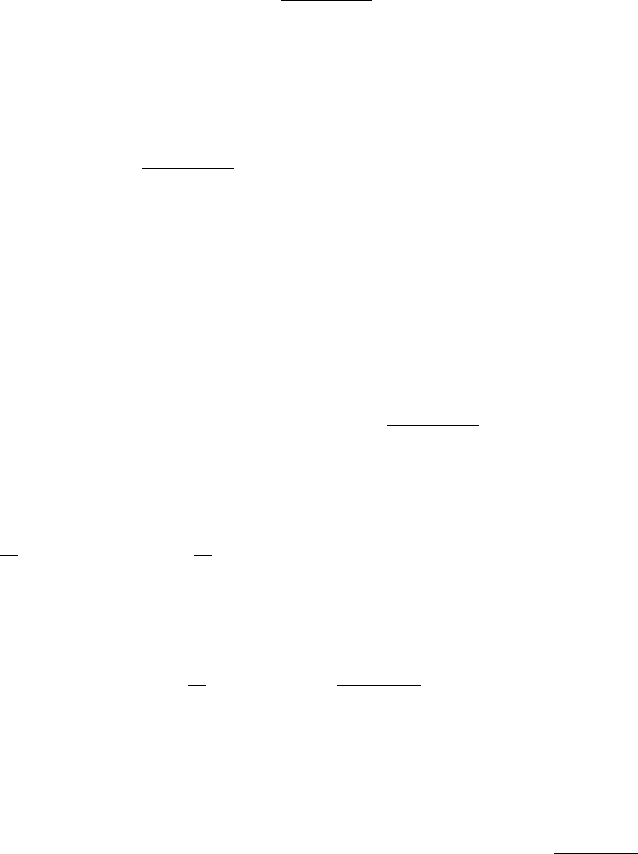
Для доказательства мы будем рассматривать интегральные суммы
специального вида и найдем их предел при
|| 0
λ
→
.
Выберем произвольное разбиение
0
{}
k
ii
x
λ
=
=
отрезка
[,]ab
. Для каж-
дого
0i =
, 1, …,
1k −
положим
1
2
ii
i
xx
ξ
+
+
=
(то есть возьмем в качестве
i
ξ
середину отрезка разбиения
1
[, ]
ii
xx
+
). В силу неравенства
1
1
, 0,1, , 1,
2
ii
ii
xx
x xi k
+
+
+
< <= −
набор точек
1
0
{}
k
ii
ξξ
−
=
=
подчинен разбиению
λ
. Найдем соответствующую
интегральную сумму:
1 11
1
1
0 00
(,) () ( )
2
k kk
ii
i i ii i i
i ii
xx
S f x x xx
λξ ξ ξ
− −−
+
+
= = =
+
= ∆= ∆= ⋅ − =
∑ ∑∑
1
2 2 2222 22
1 1 021 1
0
11
( )( )
22
k
i i kk
i
x x xxxx xx
−
+−
=
= − = −+−++− =
∑
22
22
0
1
() .
22
k
ba
xx
−
= −=
Предел рассматриваемых интегральных сумм (то есть интегральных сумм
с набором точек
ξ
специального вида) при
|| 0
λ
→
равен
22
2
ba−
. Отсюда
вытекает доказываемое соотношение.
У
ПРАЖНЕНИЕ 1. Пользуясь приемом предыдущего примера, доказать,
что при
0 ab≤<
имеет место равенство
Глава 1
32
Определенный интеграл
ç
è
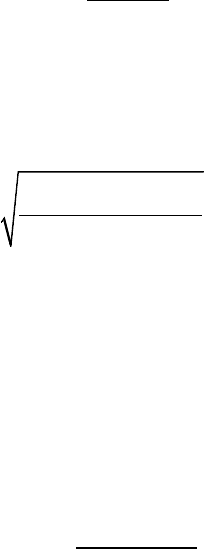
33
2
.
3
b
a
ba
x dx
−
=
∫
У
КАЗАНИЕ. Положить
22
11
,
3
i ii i
i
x xx x
ξ
++
++
=
доказать, что
1iii
xx
ξ
+
≤≤
.
У
ПРАЖНЕНИЕ 2. Доказать, что при
0 ab≤<
для любого
n∈
имеет
место равенство
11
1
.
1
b
nn
n
a
ba
x dx
n
++
+
−
=
+
∫
7. Свойства определенного интеграла как функции
промежутка интегрирования
ТЕОРЕМА 10. Предположим, что
a
,
b
,
c∈
и
abc<<
. Тогда сле-
дующие условия равносильны:
1) функция
f
интегрируема на отрезке
[,]ac
;
2) функция
f
интегрируема на каждом из отрезков
[,]ab
,
[,]bc
.
При выполнении этих условий выполняется равенство
() () () .
cbc
aab
f x dx f x dx f x dx= +
∫∫∫
Глава 1
33
Определенный интеграл
ç
è
ДОКАЗАТЕЛЬСТВО. 1) ⇒ 2). Выберем произвольное
0
ε
>
и найдем та-
кое
0
δ
>
, что из условий
([ , ])ac
λ
∈Λ
,
||
λδ
<
вытекает неравенство
( ,[ , ])S ac
ω
λε
<
. Пусть
0
λ
— разбиение отрезка
[,]ab
, удовлетворяющее
условию
0
||
λε
<
. Добавим к набору точек разбиения
0
λ
точки отрезка
[,]bc
так, чтобы при этом получилось разбиение
λ
отрезка
[,]ac
, удовле-
творяющее условию
||
λδ
<
. Допустим, что
00
{}
k
ii
x
λ
=
=
,
0
{}
l
ii
x
λ
=
=
. Как и
выше, вводим колебания функции
f
не отрезках разбиения
λ
(отрезка
[,]ac
):
1
( ,[ , ])
i ii
f xx
ωω
+
=
,
0i =
, 1, …,
1l −
. Тогда имеем:
11
0
00
( ,[ , ]) ( ,[ , ]) .
kl
ii ii
ii
S ab x x S ac
ωω
λ ωω λε
−−
= =
= ∆≤ ∆= <
∑∑
Из оценки
0
( ,[ , ])S ab
ω
λε
<
по критерию интегрируемости функции выво-
дим, что функция
f
является интегрируемой на отрезке
[,]ab
. Аналогично
рассматривается отрезок
[,]bc
.
2) ⇒ 1) Предположим, что функция
f
интегрируема на каждом из
отрезков
[,]ab
,
[,]bc
. Тогда она ограничена на каждом из этих отрезков, а,
следовательно, и на всем отрезке
[,]ac
. Выберем такую константу
M
, что
для любого
[,]x ac∈
выполняется неравенство
| ( )|fx M≤
.
Выберем произвольное
0
ε
>
и найдем такое
0
δ
>
, чтобы выполня-
лись следующие условия:
для любого
1
([ , ])ab
λ
∈Λ
, такого, что
1
||
λδ
<
выполняется неравенст-
во
1
( ,[ , ])S ab
ω
λε
<
;
для любого
2
([ , ])bc
λ
∈Λ
, такого, что
2
||
λδ
<
выполняется неравен-
ство
2
( ,[ , ])S bc
ω
λε
<
.
Глава 1
34
Определенный интеграл
ç
è
Уменьшая в случае необходимости число
δ
, будем считать, что выполня-
ется неравенство
δε
≤
. Возьмем любое разбиение
([ , ])ac
λ
∈Λ
, удовле-
творяющее условию
||
λδ
<
. Найдем оценки для величины
( ,[ , ])S ac
ω
λ
. Эти
оценки будут разными, в зависимости от того, находится или нет проме-
жуточная точка
b
среди точек разбиения
λ
.
С
ЛУЧАЙ 1. Точка
b
находится среди точек разбиения
λ
.
Обозначим через
1
λ
(
2
λ
) множество всех точек разбиения
λ
, попа-
дающих в отрезок
[,]ab
(соответственно, в отрезок
[,]bc
). Тогда
1
λ
(
2
λ
)
будет разбиением соответствующего отрезка. Очевидно, что выполняется
оценка
1
| || |
λλ
≤
(потому, что каждый из отрезков разбиения
1
λ
является в
то же время и отрезком разбиения
λ
). Поэтому выполняется оценка
1
||
λδ
<
. Из аналогичных соображений получаем, что
2
||
λδ
<
. Допустим,
что
0
{}
k
ii
x
λ
=
=
, .
10
{}
l
ii
x
λ
=
=
,
2
{}
k
iil
x
λ
=
=
.
Обращаем внимание читателя, что имеет место равенство
k
xb=
, и
эта точка является последней точкой разбиения
1
λ
и первой точкой раз-
биения
2
λ
. Далее имеем,
111
00
( ,[ , ])
klk
ii ii ii
i i il
S ac x x x
ω
λ ωωω
−− −
= = =
= ∆= ∆+ ∆=
∑∑∑
12
( ,[ , ]) ( ,[ , ]).S ab S bc
ωω
λλ
= +
Из оценок
1
||
λδ
<
,
2
||
λδ
<
следует, что
1
( ,[ , ])S ab
ω
λε
<
,
2
( ,[ , ])S bc
ω
λε
<
и, следовательно,
( ,[ , ]) 2S ac
ω
λε
<
.
Глава 1
35
Определенный интеграл
ç
è
СЛУЧАЙ 2. Точка
b
не является одной из точек разбиения
λ
.
Рассмотрим множество всех точек разбиения
λ
, попадающих в отре-
зок
[,]ab
. Добавляя к этому множеству точку
b
, мы получим разбиение
отрезка
[,]ab
, которое обозначим через
1
λ
. Отметим, что выполняется не-
равенство
1
||
λδ
<
. Действительно, все отрезки разбиения
1
λ
, кроме по-
следнего, совпадают с одним из отрезков разбиения
λ
. Поэтому длины
этих отрезков меньше, чем
δ
. Последний отрезок разбиения
1
λ
является
частью отрезка разбиения
λ
. Следовательно, длина этого последнего от-
резка также меньше, чем
δ
. Аналогично, добавляя к точкам разбиения
λ
,
попадающим в отрезок
[,]bc
, точку
b
, получим разбиение отрезка
[,]bc
,
которое обозначим через
2
λ
. По аналогии с предыдущим случаем доказы-
вается, что
2
||
λδ
<
.
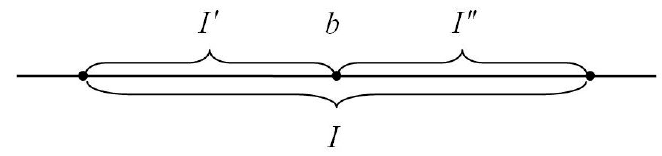
Рассмотрим отрезок
I
разбиения
λ
, внутри которого находится точ-
ка
b
. Этот отрезок делится точкой
b
на два отрезка, которые мы обозна-
чим через
I
′
и
I
′′
(см. рисунок ниже).
Рассмотрим сумму
( ,[ , ])S ac
ω
λ
и сравним ее с суммой
12
( ,[ , ]) ( ,[ , ])S ab S bc
ωω
λλ
+
.
Для перехода от одного выражения к другому нужно в сумме
( ,[ , ])S ac
ω
λ
удалить слагаемое, отвечающее отрезку
I
разбиения
λ
, заменив его двумя
слагаемыми, отвечающими отрезкам
I
′
и
I
′′
разбиений
1
λ
и
2
λ
соответст-
Глава 1
36
Определенный интеграл
ç
è
венно. Обозначим через
ω
,
ω
′
,
ω
′′
колебания функции
f
на отрезках
I
,
I
′
и
I
′′
соответственно. Как обычно, через
||I
обозначается длина отрезка
.I
Тогда, в силу сказанного, имеет место соотношение
12
( ,[ , ]) ( ,[ , ]) ( ,[ ,|| || ]|| ).S ac SI bI SI ab c
ω ωω
λ λλω ωω
′′ ′′′
−+ +⋅ +
′
⋅⋅ =
Красным цветом в формуле показано удаляемое слагаемое, а зеленым цве-
том — два добавляемых слагаемых. Отсюда получаем:
1
0
2
0
( ,[ , ]) ( ,[ , ]) ( ,[ , ]) ||| | ||S ac S ab Ib IS cI
ωω ω
ωω ωλλ λ
≥≥
= + +⋅ − − ≤
′ ′ ′′ ′′
⋅⋅
12
( ,[ , ]) ( ,[ , ]) | |.S ab S bc I
ωω
λ λω
≤ + +⋅
Неравенство возникает после отбрасывания двух выделенных красным
цветом слагаемых. Остается заметить, что, как и в предыдущем случае, вы-
полняется неравенство
12
( ,[ , ]) ( ,[ , ])S ab S bc
ωω
λ λε
+ <2
. Кроме того, имеют
место неравенства
2M
ω
≤
,
|| 2I
δε
<≤
. Окончательно получаем оценку
( ,[ , ]) 2 4S ac M
ω
λ εε
<+
.
Итак, в любом из двух случаев выполняется оценка
( ,[ , ]) 2 4S ac M
ω
λ εε
<+
.
В силу произвольности
ε
, из критерия интегрируемости функции следует,
что функция
f
интегрируема на отрезке
[,]ac
.
Перейдем теперь к соотношениям, связывающим интегралы. Выбе-
рем произвольное разбиение
([ , ])ac
λ
∈Λ
, удовлетворяющее дополнитель-
ному условию
b
λ
∈
. Выберем набор точек
ξ
, подчиненный разбиению
.
λ
Глава 1
37
Определенный интеграл
ç
è
Рассмотрим интегральную сумму
1
0
()
l
ii
i
fx
ξ
−
=
∆
∑
. Разбивая сумму в правой
части на две суммы, соответствующие каждому из двух отрезков
[,]ab
и
[,]bc
, получаем:
1 11
00
() () () .
lkl
ii ii ii
i i ik
fx fx fx
ξξξ
− −−
= = =
∆= ∆+ ∆
∑∑∑
В правой части находятся интегральные суммы для функции
f
на
отрезках
[,]ab
и
[,]bc
соответственно. Переходя к пределу при условиях
|| 0
λ
→
,
b
λ
∈
, получаем искомое соотношение для интегралов.
Теорема полностью доказана.
Выше мы рассматривали определенный интеграл
()
b
a
f x dx
∫
в предпо-
ложении, что
ab<
. Понятие определенного интеграла может быть расши-
рено на случай других соотношений между верхним и нижним пределами.
Предположим, что функция
f
определена и интегрируема на неко-
тором отрезке
I
. Для
a
,
bI∈
,
ab>
полагаем по определению
() () , () 0.
b aa
a ba
f x dx f x dx f x dx
=−=
∫ ∫∫
Тогда утверждение теоремы может быть обобщено на такой случай.
С
ЛЕДСТВИЕ ТЕОРЕМЫ 10. Предположим, что функция
f
интегрируе-
ма на некотором отрезке
I
. Тогда для любых
a
,
b
,
cI∈
выполняется ра-
венство
Глава 1
38
Определенный интеграл
ç
è
() () () .
cbc
aab
f x dx f x dx f x dx= +
∫∫∫
Д
ОКАЗАТЕЛЬСТВО. Случай
abc<<
рассмотрен в самой теореме. Рас-
смотрим случай, когда
acb<<
. Применяя теорему, получаем:
() () () .
bcb
aac
f x dx f x dx f x dx= +
∫∫∫
Меняя местами пределы интегрирования во втором интеграле в правой
части, получаем:
() () ()
bcc
aab
f x dx f x dx f x dx= −
∫∫∫
.
Перенося второй интеграл в правой части равенства в левую часть, полу-
чим требуемое утверждение. Остальные случаи рассматриваются анало-
гично.
Теорема 10 позволяет найти еще один расширить класс интегрируе-
мых функций. Приведем сначала следующее определение.
О
ПРЕДЕЛЕНИЕ. Функция, определенная на отрезке
I
, называется ку-
сочно-непрерывной на этом промежутке, если она непрерывна всюду на
,I
кроме конечного числа точек, в которых имеет разрывы первого рода.
Т
ЕОРЕМА 11. Функция, кусочно-непрерывная на отрезке, интегрируе-
ма на этом отрезке.
Д
ОКАЗАТЕЛЬСТВО. Ограничимся предположением, что функция
f
определена на отрезке
[,]ab
и непрерывна всюду, кроме одной точки
c
,
Глава 1
39
Определенный интеграл
ç
è
acb<<
. Рассмотрим сужение функции
f
на отрезок
[,]ac
. Эта функция
непрерывна во всех точках
x
,
axc≤<
и существует предел
0
lim ( )
xc
fx
→−
. В
силу следствия теоремы 9, функция
f
интегрируема на отрезке
[ , ].ac
Ана-
логично получаем, что она интегрируема на отрезке
[,]cb
. Из теоремы 10
выводим, что функция
f
интегрируема на отрезке
[,]ab
.
Теорема доказана.
8. Теорема о среднем для определенного интеграла
Рассмотрим сначала некоторые неравенства для определенных инте-
гралов.
Т
ЕОРЕМА 12. Предположим, что функция
f
определена и интегри-
руема на отрезке
[,]ab
и для всех
[,]x ab∈
выполняется неравенст-
во
() 0fx≥
. Тогда
() 0
b
a
f x dx ≥
∫
.
Д
ОКАЗАТЕЛЬСТВО. Выберем произвольное разбиение
λ
отрезка
[ , ],ab
возьмем произвольный набор точек
ξ
,
|
ξλ
и рассмотрим соответствую-
щую интегральную сумму
1
0
()
k
ii
i
fx
ξ
−
=
∆
∑
. Все слагаемые под знаком суммы
являются неотрицательными. Поэтому
1
0
() 0
k
ii
i
fx
ξ
−
=
∆≥
∑
. Переходя к пределу
при
|| 0
λ
→
получаем требуемое неравенство для определенного интегра-
ла.
Глава 1
40
Определенный интеграл
ç
è
