Овчаров Л.А. и др. Математические модели информационых процессов и управления
Подождите немного. Документ загружается.

128
KK K
FF F
1
0
2
0
3
0
00
10
100
001
011
10 1
1111
0111
0000
10 11
0011
0001
=
=
=
;; .
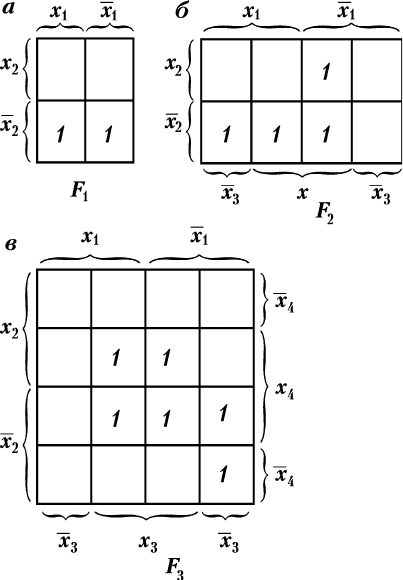
ä‡Ú˚ ÇÂȘ‡ ‰Îfl ÙÛÌ͈ËË ‰‚Ûı, ÚÂı Ë ˜ÂÚ˚Âı ‡„ÛÏÂÌÚÓ‚
Ô˂‰ÂÌ˚ ̇ ËÒ. 3.7, ‡, · Ë ‚ ÒÓÓÚ‚ÂÚÒÚ‚ÂÌÌÓ. äÎÂÚÍË, ÓÚÏÂ-
˜ÂÌÌ˚ ̇ ͇ڇı ‰ËÌˈ‡ÏË, ÒÓÓÚ‚ÂÚÒÚ‚Û˛Ú ‚¯ËÌ‡Ï 0-ÍÛ·Ó‚,
Ú.Â. ÍÓÌÒÚËÚÛÂÌÚ‡Ï Â‰ËÌˈ˚.
Ç ‰‡Î¸ÌÂȯÂÏ ÔË ËÁÓ·‡ÊÂÌËË Í‡Ú ÇÂȘ‡ ËÌ‚ÂÒÌ˚Â
Á̇˜ÂÌËfl ‡„ÛÏÂÌÚÓ‚ (ı
1
, ı
2
,..., x
n
) ·Û‰ÛÚ ÓÔÛÒ͇ڸÒfl.
êàë. 3.7
129
ä‡Ú˚ ÇÂȘ‡ – Û‰Ó·ÌÓ Ò‰ÒÚ‚Ó ‰Îfl ‡Ì‡ÎËÁ‡ ·Û΂˚ı
ÙÛÌ͈ËÈ Ë Ëı ‚Á‡ËÏÓÒ‚flÁÂÈ ÔË Ì·Óθ¯ÓÏ ˜ËÒΠ‡„ÛÏÂÌ-
ÚÓ‚.
ÑÎfl ‡Ì‡ÎËÁ‡ ÒÎÓÊÌ˚ı ÙÛÌ͈ËÈ, ·Óθ¯Ó„Ó ˜ËÒ· Ô ÂÏÂÌ-
Ì˚ı ˆÂÎÂÒÓÓ·‡ÁÌÓ ËÒÔÓθÁÓ‚‡Ú¸ ‡Ì‡ÎËÚ˘ÂÒÍË ÏÂÚÓ‰˚ Ò Â‡-
ÎËÁ‡ˆËÂÈ Ëı ̇ ùÇå. Ä̇ÎËÚ˘ÂÒÍË ÏÂÚÓ‰˚ ‡Ì‡ÎËÁ‡ ·Û΂˚ı
ÙÛÌ͈ËÈ Ô‰ÔÓ·„‡˛ Ú Ì‡Î˘Ë ÓÔ‰ÂÎÂÌÌ˚ı ͇ÌÓÌ˘ÂÒÍËı
ÙÓÏ. í‡ÍËÏË Í‡ÌÓÌ˘ÂÒÍËÏË, ËÒıÓ‰Ì˚ÏË ÙÓχÏË ‰Îfl ‡Ì‡ÎË-
Ú˘ÂÒÍËı ÏÂÚÓ‰Ó‚ fl‚Îfl˛ÚÒfl Òӂ¯ÂÌÌ˚ ÌÓχθÌ˚ ÙÓÏ˚
ÙÛÌ͈ËË (ëçî).
í Â Ó Â Ï ‡. ã˛·‡fl ·Û΂‡ ÙÛÌ͈Ëfl ÏÓÊÂÚ ·˚Ú¸ Ô‰ÒÚ‡‚ÎÂ-
̇ ‚ ‰‚Ûı ÙÓχı: ÎË·Ó ‚ Òӂ¯ÂÌÌÓÈ ‰ËÁ˙˛ÌÍÚË‚ÌÓÈ ÌÓ-
χθÌÓÈ ÙÓÏ (ëÑçî), Ú.Â. ‚ ‚ˉ ‰ËÁ˙˛Ì͈ËË ÍÓÌÒÚËÚÛÂÌÚ
‰ËÌˈ˚; ÎË·Ó ‚ Òӂ¯ÂÌÌÓÈ ÍÓÌ˙˛ÌÍÚË‚ÌÓÈ ÌÓχθÌÓÈ
ÙÓÏ (ëäçî), Ú.Â. ÍÓÌ˙˛Ì͈ËË ÍÓÌÒÚËÚÛÂÌÚ ÌÛÎfl.
Ñ Ó Í ‡ Á ‡ Ú Â Î ¸ Ò Ú ‚ Ó . ê‡ÒÒÏÓÚËÏ ÔÓËÁ‚ÓθÌÛ˛ ÙÛÌÍˆË˛
ÚÂı ‡„ÛÏÂÌÚÓ‚, Á‡‰‡ÌÌÛ˛ Ú‡·Î. 3.8.
îÛÌ͈Ëfl ÓÔ‰ÂÎÂ̇ ̇ ‚ÓÒ¸ÏË Ì‡·Ó‡ı, ̇ ÔflÚË Ì‡·Ó‡ı
Ó̇ ‡‚̇ ‰ËÌˈÂ. ç‡ ÚÂı ̇·Ó‡ı, ̇ ÍÓÚÓ˚ı ÙÛÌ͈Ëfl
‡‚̇ ‰ËÌˈÂ,  ÏÓÊÌÓ Ô‰ÒÚ‡‚ËÚ¸ ‚ ‚ˉ ‰ËÁ˙˛Ì͈ËË ÍÓÌ-
ÒÚËÚÛÂÌÚ Â‰ËÌˈ˚:
Fxxx xxx xxx xxx(, , )
1 23 1 23 1 23 1 23
= ⋅⋅∨⋅⋅∨⋅⋅∨
∨⋅ ⋅ ∨⋅ ⋅xxx xxx
1 23 1 23
.
èÓ‰ÒÚ‡‚Ë‚ ‚ ˝ÚÓ ‚˚‡ÊÂÌË ̇·Ó˚ ÔÂÂÏÂÌÌ˚ı, ̇ ÍÓÚÓ-
˚ı ÙÛÌ͈Ëfl ‡‚̇ ‰ËÌˈ (ÒÏ. Ú‡·Î. 3.8), ÏÓÊÌÓ Û·Â‰ËÚ¸Òfl ‚
‡‰ÂÍ‚‡ÚÌÓÒÚË Ú‡·Î˘ÌÓ„Ó Á‡‰‡ÌËfl ÙÛÌ͈ËË Ë Á‡‰‡ÌËfl ÙÛÌ͈ËË
‚ Òӂ¯ÂÌÌÓÈ ‰ËÁ˙˛ÌÍÚË‚ÌÓÈ ÌÓχθÌÓÈ ÙÓÏÂ.
èÓ͇ÊÂÏ ˝ÚÓ ‰Îfl ÔÓËÁ‚ÓθÌÓÈ ÙÛÌ͈ËË n-‡„ÛÏÂÌÚÓ‚. ÑÎfl
˝ÚÓ„Ó ÔÂÂÔ˯ÂÏ ‚˚‡ÊÂÌË (3.9) ‚ ÒËÏ‚Ó΢ÂÒÍÓÈ ÙÓÏÂ:
F(x
1
, x
2
, x
3
) = m
0
∨ m
2
∨ m
4
∨ m
5
∨ m
7
, (3.10)
„‰Â m
i
ÓÔ‰ÂÎÂÌ˚ ‚ Ú‡·Î. 3.8.
퇷Îˈ‡ 3.8
ı
1
ı
2
ı
3
F
0001
001 0
0 1 0 1
0 110
1 001
1 0 11
1100
1111
130
ǂ‰ÂÏ Á‡ÚÂÏ ÌÂÍÓÚÓÛ˛ ·ÛÎÂ‚Û ÙÛÌÍˆË˛ f
i
, ÚÓ„‰‡ ‰Îfl
ÙÛÌ͈ËÈ ÚÂı ‡„ÛÏÂÌÚÓ‚ ÏÓÊÌÓ Á‡ÔËÒ‡Ú¸
F(x
1
, x
2
, x
3
) = f
0
⋅m
0
∨ f
1
⋅m
1
∨ f
2
⋅m
2
∨ f
3
⋅m
3
∨ f
4
⋅m
4
∨ f
5
×
× m
5
∨ f
6
⋅m
6
∨ f
7
⋅m
7
. (3.11)
ÑÎfl ÙÛÌ͈ËË F, Á‡‰‡ÌÌÓÈ Ú‡·Î. 3.8, ÙÛÌ͈Ëfl f
i
̇ ̇·Ó‡ı
(0, 2, 4, 5, 7) ·Û‰ÂÚ ‡‚̇ ‰ËÌˈÂ, ‡ ̇ ÓÒڇθÌ˚ı ̇·Ó‡ı –
ÌÛβ.
í‡ÍËÏ Ó·‡ÁÓÏ, ‰Îfl ÙÛÌ͈ËÈ n-‡„ÛÏÂÌÚÓ‚ ÏÓÊÌÓ Á‡ÔËÒ‡Ú¸
Fx x x f m
n
i
n
ii
(, , , ) .
1 2
0
2 1
K = ⋅
=
−
V
(3.12)
ᇉ‡‚‡fl ‡Á΢Ì˚ Á̇˜ÂÌËfl f
i
̇ ‡Á΢Ì˚ı ̇·Ó‡ı ‡„Û-
ÏÂÌÚÓ‚, ÏÓÊÌÓ ÔÓÎÛ˜ËÚ¸ β·Û˛ ÙÛÌÍˆË˛ n-‡„ÛÏÂÌÚÓ‚ ËÁ Ó·-
˘Â„Ó ÍÓ΢ÂÒÚ‚‡
2
2
n
. íÂÔ¸ ÌÂÓ·ıÓ‰ËÏÓ ÔÂÂÈÚË ÓÚ ëÑçî Í
ëäçî, Ú.Â. ÔÓÎÛ˜ËÚ¸ ‰Û‡Î¸ÌÛ˛ ÙÓÏÛ ÙÛÌ͈ËË. ÑÎfl ˝ÚÓ„Ó
‡ÒÒÏÓÚËÏ ËÌ‚ÂÒ˲ ‚˚‡ÊÂÌËfl (3.12):
Fx x x f m
n
i
n
ii
(, , , ) .
1 2
0
2 1
K = ⋅
=
−
V
(3.13)
ç‡ÔËÏÂ, ‰Îfl ÙÛÌ͈ËË, Á‡‰‡ÌÌÓÈ Ú‡·Î. 3.8, ËÌ‚Â Ò̇fl ÂÈ
ÙÛÌ͈Ëfl
Fxx x xxx xxx xxx(, , )
1 23 1 23 1 23 1 23
= ⋅⋅∨⋅⋅∨⋅⋅
ËÎË
Fx x x m m m(, , ) ,
1 23 1 36
= ∨∨
Ú.Â. ˝ÚÓ ÙÛÌ͈Ëfl, Á‡ÔËÒ‡Ì̇fl ‚ ëÑçî ̇ ÚÂı ̇·Ó‡ı, ̇ ÍÓ-
ÚÓ˚ı Ó̇ ‡‚̇ ÌÛβ.
èËÏÂÌË‚ Í ‚˚‡ÊÂÌ˲
(3.13) ÚÂÓÂÏÛ ‰Â åÓ„‡Ì‡, ÔÓÎÛ˜ËÏ
Fx x x f m
n
i
n
ii
(, , , ) ( ).
1 2
0
2 1
K = ∨
=
−
& (3.14)
íÂÔ¸ ÌÂÓ·ıÓ‰ËÏÓ ‚ ‚˚‡ÊÂÌËË (3.14) Á‡ÏÂÌËÚ¸ ÍÓÌÒÚËÚÛ-
ÂÌÚÛ Â‰ËÌˈ˚ m
i
̇ ÍÓÌÒÚËÚÛÂÌÚÛ ÌÛÎfl M
j
. ÑÎfl ˝ÚÓ„Ó ÏÓÊÌÓ
‚ÓÒÔÓθÁÓ‚‡Ú¸Òfl ͇ڇÏË ÇÂȘ‡.
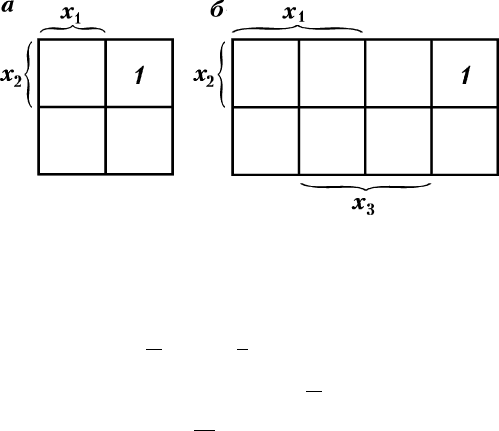
ç‡ Í‡ Ú ÇÂȘ‡ ‰Îfl ÙÛÌ͈ËÈ ‰‚Ûı ÔÂÂÏÂÌÌ˚ı (ÒÏ. ËÒ.
3.7) ÓÚÏÂÚËÏ ÒËÏ‚ÓÎÓÏ “1”, ̇ÔËÏÂ, ÍÓÌÒÚËÚÛÂÌÚÛ Â‰ËÌˈ˚
m
1
. Ç ÒÓÓÚ‚ÂÚÒÚ‚ËË Ò ÓÔ‰ÂÎÂÌËÂÏ ÇÂÌ̇ ËÌ‚ÂÒËfl m
1
‡‚̇
mxx M
1122
= ∨ = .
131
ç‡ Í‡ Ú ÇÂȘ‡ ‰Îfl ÙÛÌ͈ËÈ ÚÂı ÔÂÂÏÂÌÌ˚ı (ËÒ. 3.8)
ÓÚÏÂÚËÏ ÍÓÌÒÚËÚÛÂÌÚÛ Â‰ËÌˈ˚ m
2
. àÌ‚ÂÒËfl m
2
·Û‰ÂÚ ‡‚̇
mxxxM
2 1 23 5
= ∨∨= .
чÎÂÂ, ÔÓ Ë̉Û͈ËË ÔÓÎÛ˜ËÏ, ˜ÚÓ
mM
in
i
=
−−2 1
, Ë Ì‡Ó·ÓÓÚ,
Mm
in
i
=
−−2 1
. (3.15)
á‡ÏÂÌË‚ ‚ ‚˚‡ÊÂÌËË (3.14) ÍÓÌÒÚËÚÛÂÌÚ˚ ‰ËÌˈ˚ ̇ ÍÓÌ-
ÒÚËÚÛÂÌÚ˚ ÌÛÎfl, ‚ ÒÓÓÚ‚ÂÚÒÚ‚ËË Ò ÒÓÓÚÌÓ¯ÂÌËflÏË (3.15) ÓÍÓÌ-
˜‡ÚÂθÌÓ ÔÓÎÛ˜ËÏ
Fx x x f M
i
n
in
i
(, , ) ( ).
1 23
0
2 1
2 1
= ∨
=
−
−−
&
(3.16)
ç‡ÔËÏÂ, ÔÓÎÛ˜Â̇ ëÑçî ÙÛÌ͈ËË ÚÂı ÔÂÂÏÂÌÌ˚ı
Fxxx mmmm(, , ) .
1 23 0257
= ∨∨∨ (3.17)
í·ÛÂÚÒfl ̇ÈÚË ëäçî ˝ÚÓÈ ÙÛÌ͈ËË. á‡Ô˯ÂÏ ‚˚‡ÊÂ-
ÌË (3.17) ‚ ‚ˉ ‰ËÁ˙˛Ì͈ËË ÔÓËÁ‚‰ÂÌËÈ f
i
̇ ÒÓÓÚ‚ÂÚÒÚ-
‚Û˛˘Ë ÍÓÌÒÚËÚÛÂÌÚ˚ ‰ËÌˈ˚:
Fxxx mmmm(, , )
1 23 0 1 23
1 0 1 0= ⋅∨⋅∨⋅∨⋅∨
∨⋅ ∨⋅ ∨⋅ ∨⋅0 1 00
4567
mmmm. (3.18)
àÁ ‚˚‡ÊÂÌËfl (3.18) ‚ˉÌÓ, ˜ÚÓ Ì‡ ̇·Ó‡ı (0, 2, 5, 7)
f
i
= 1, ‡ ̇ ̇·Ó‡ı (1, 3, 4, 6) f
i
= 0.
èÓ‰ÒÚ‡‚Ë‚ ÔÓÎÛ˜ÂÌÌ˚ Á̇˜ÂÌËfl f
i
‚ ‚˚‡ÊÂÌË 3.16 Ë Ì‡È-
‰fl Á̇˜ÂÌËfl ÍÓ˝ÙÙˈËÂÌÚÓ‚ ÍÓÌÒÚËÚÛÂÌÚ ÌÛÎfl, ÔÓÎÛ˜ËÏ ëäçî
Á‡‰‡ÌÌÓÈ ÙÛÌ͈ËË:
êàë. 3.8
132
Fxxx MMMM(, , ) .
1 23 6431
= ⋅⋅⋅ (3.19)
íÂÓÂχ “Ó ‰‚Ûı ÙÓχı” ËÏÂÂÚ ·Óθ¯Ó Á̇˜ÂÌËÂ, Ú‡Í Í‡Í
ÔÓ͇Á˚‚‡ÂÚ, ˜ÚÓ Î˛·Û˛ ÙÛÌÍˆË˛ ÏÓÊÌÓ Á‡ÔËÒ‡Ú¸ ÎË·Ó Ò ÔÓ-
ÏÓ˘¸˛ ÍÓÌÒÚËÚÛÂÌÚ ÌÛÎfl, ÎË·Ó Ò ÔÓÏÓ˘¸˛ ÍÓÌÒÚËÚÛÂÌÚ Â‰ËÌË-
ˆ˚. ùÚË ‰‚ ͇ÌÓÌ˘ÂÒÍË ÙÓÏ˚ ÙÛÌ͈ËË Ì ËÏÂ˛Ú Ò‡ÏÓÒÚÓfl-
ÚÂθÌÓ„Ó Á̇˜ÂÌËfl, Ӊ̇ÍÓ ÓÌË fl‚Îfl˛ÚÒfl ËÒıÓ‰Ì˚ÏË ‰Îfl ·Óθ-
¯ËÌÒÚ‚‡ ÏÂÚÓ‰Ó‚ ‡Ì‡ÎËÁ‡ ·Û΂˚ı ÙÛÌ͈ËÈ.
äÓÏ ÚÓ„Ó, ÚÂÓÂχ “Ó ‰‚Ûı ÙÓχı” ËÏÂÂÚ Ó˜Â̸ ‚‡ÊÌÓÂ
ÒΉÒÚ‚ËÂ. é̇ ÔÓÁ‚ÓÎflÂÚ ÔÓÎÛ˜ËÚ¸ Ó‰ÌÛ ËÁ ÙÛÌ͈ËÓ̇θÌÓ
ÔÓÎÌ˚ı ÒËÒÚÂÏ ËÎË ·‡ÁËÒÓ‚.
é Ô Â ‰ Â Î Â Ì Ë Â. ëËÒÚÂχ ·Û΂˚ı ÙÛÌ͈ËÈ Ì‡Á˚‚‡ÂÚÒfl
ÔÓÎÌÓÈ, ÂÒÎË Ò ÔÓÏÓ˘¸˛ ÙÛÌ͈ËÈ, ‚ıÓ‰fl˘Ëı ‚ ˝ÚÛ ÒËÒÚÂÏÛ,
ÔËÏÂÌflfl ÓÔ‡ˆËË ÒÛÔÂÔÓÁˈËË Ë ÔÓ‰ÒÚ‡ÌÓ‚ÍË, ÏÓÊÌÓ ÔÓÎÛ-
˜ËÚ¸ β·Û˛ ÒÍÓθ Û„Ó‰ÌÓ ÒÎÓÊÌÛ˛ ·ÛÎÂ‚Û ÙÛÌÍˆË˛.
Ç ÒÓÓÚ‚ÂÚÒÚ‚ËË Ò ÚÂÓÂÏÓÈ ‚ ˝ ÚÛ ÒËÒÚÂÏÛ ‚ıÓ‰flÚ: ‰ËÁ˙˛ÌÍ-
ˆËfl; ÍÓÌ˙˛Ì͈Ëfl Ë ËÌ‚ÂÒËfl. ùÚÛ ÒËÒÚÂÏÛ ËÌÓ„‰‡ ̇Á˚‚‡˛Ú
ÓÒÌÓ‚Ì˚Ï ·‡ÁËÒÓÏ.
îÛÌ͈ËÓ̇θÌÓ ÔÓÎÌÛ˛ ÒËÒÚÂÏÛ, ÒÓÒÚÓfl˘Û˛ ËÁ ÙÛÌ͈ËÈ
“̇‚ÌÓÁ̇˜ÌÓÒÚ¸, ÍÓÌ˙˛Ì͈Ëfl Ë ÍÓÌÒÚ‡ÌÚ‡ ‰ËÌˈ‡”, ÔÓÁ‚Ó-
ÎflÂÚ ÔÓÎÛ˜ËÚ¸ ÚÂÓÂχ Ü„‡ÎÍË̇.
íÂÓÂχ Ü„‡ÎÍË̇. ã˛·‡fl ·Û΂‡ ÙÛÌ͈Ëfl ÏÓÊÂÚ ·˚Ú¸
Ô‰ÒÚ‡‚ÎÂ̇ ‚ ‚ˉ ÔÓÎËÌÓχ:
F(x
1
, x
2
,..., x
n
) = a
0
g a
1
⋅x
1
g a
2
⋅x
2
g ... g a
n
⋅x
n
g
g a
n+1
x
1
⋅x
2
g a
n
+ 2x
1
⋅x
3
g ... g a
N
x
1
⋅x
2
⋅x
3
...x
n
, (3.20)
„‰Â ‡
0
, ‡
1
,..., a
N
– ÌÂÍÓÚÓ˚ ÍÓ˝ÙÙˈËÂÌÚ˚, ‡‚Ì˚ 0 ËÎË 1.
è‰ÔÓÎÓÊËÏ, ˜ÚÓ Á‡‰‡Ì‡ ÔÓËÁ‚Óθ̇fl ·Û΂‡ ÙÛÌ͈Ëfl
n-‡„ÛÏÂÌÚÓ‚ F(x
1
, x
2
,..., x
n
), ‡‚̇fl ‰ËÌˈ ̇ ÌÂÍÓÚÓÓÏ
˜ËÒΠ‡„ÛÏÂÌÚÓ‚ Ò ÌÓχÏË (1, 2, 3,..., i,..., p).
èÓ͇ÊÂÏ, ˜ÚÓ ·Û΂‡ ÙÛÌ͈Ëfl ÏÓÊÂÚ ·˚Ú¸ Á‡ÔË҇̇ ‚ ‚ˉÂ
ÓÚˈ‡ÌËfl ‡‚ÌÓÁ̇˜ÌÓÒÚË (Ì ‡‚ÌÓÁ̇˜ÌÓÒÚË) ÍÓÌÒÚËÚÛÂÌÚ
‰ËÌˈ˚ ̇ ÚÂı Ê ̇·Ó‡ı, ̇ ÍÓÚÓ˚ı ‰‡Ì̇fl ÙÛÌ͈Ëfl ‡‚-
̇ ‰ËÌˈÂ, Ú.Â. ‚ ‚ˉÂ
F(x
1
, x
2
,..., x
n
) = m
1
g m
2
g m
3
g ... g m
i
g ... g m
p
. (3.21)
ÑÂÈÒÚ‚ËÚÂθÌÓ, ÂÒÎË Í‡Í‡fl-ÎË·Ó ËÁ ÍÓÌÒÚËÚÛÂÌÚ Â‰ËÌˈ˚
‡‚̇ ‰ËÌˈÂ, ÚÓ ÓÒڇθÌ˚ ‡‚Ì˚ ÌÛβ. ç‡ÔËÏÂ, ‰Îfl ̇-
·Ó‡ Ò ÌÓÏÂÓÏ i ÔÓÎÛ˜ËÏ
m
1
g m
2
g ... g m
i
g ... g m
p
= 0 g 0 g ... g
g 1 g ... g 0 = 1. (3.22)
àÒÔÓθÁÛfl ‚˚‡ÊÂÌË (3.21), ÏÓÊÌÓ ÔÂÂÈÚË Í ÙÓÏÂ

133
(3.20). ÑÎfl ˝ ÚÓ„Ó ‰ÓÒÚ‡ÚÓ˜ÌÓ Ô‰ÒÚ‡‚ËÚ¸ ÍÓÌÒÚËÚÛÂÌÚ˚ ‰ËÌË-
ˆ˚ ‚ ‚ˉ ÍÓÌ˙˛Ì͈ËË ‡„ÛÏÂÌÚÓ‚, Á‡ÏÂÌËÚ¸ ‚Ò ËÌ‚ÂÒÌ˚Â
Á̇˜ÂÌËfl ‡„ÛÏÂÌÚÓ‚ ‚ ÒÓÓÚ‚ÂÚÒÚ‚ËË Ò ‚˚‡ÊÂÌËÂÏ (3.2), ÔÂ-
ÂÏÌÓÊËÚ¸ Ë ÔË‚ÂÒÚË ÔÓ‰Ó·Ì˚ ˜ÎÂÌ˚ ‚ ÒÓÓÚ‚ÂÚÒÚ‚ËÂ Ò ‚˚-
‡ÊÂÌËÂÏ (3.5).
ç‡ÔËÏÂ, ‰‡ÌÓ
m xxxx
11234
= ⋅⋅⋅.
á‡ÏÂÌË‚ ËÌ‚ÂÒÌ˚ Á̇˜ÂÌËfl ‡„ÛÏÂÌÚÓ‚, ÔÓÎÛ˜ËÏ
m
i
= (1 g x
1
)⋅x
2
⋅x
3
⋅(1 g x
4
).
ê‡ÒÍ˚‚ ÒÍÓ·ÍË Ë Ô˂‰fl ÔÓ‰Ó·Ì˚ ˜ÎÂÌ˚, ÔÓÎÛ˜ËÏ Á‡ÔËÒ¸
ÙÛÌ͈ËË ‚ ÙÓÏ ÏÌÓ„Ó˜ÎÂ̇:
m
i
= x
2
⋅x
3
g x
1
⋅x
2
⋅x
3
g x
2
⋅x
3
⋅x
4
g x
1
⋅x
2
⋅x
3
⋅x
4
.
í‡ÍËÏ Ó·‡ÁÓÏ, ‰Îfl ÚÓ„Ó, ˜ÚÓ·˚ Á‡ÔËÒ‡Ú¸ ÙÛÌÍˆË˛ ‚ ‚ˉÂ
ÏÌÓ„Ó˜ÎÂ̇, ÌÂÓ·ıÓ‰ËÏÓ Ô‰ÒÚ‡‚ËÚ¸  ‚ ‚ˉ ÓÚˈ‡ÌËfl ‡‚-
ÌÓÁ̇˜ÌÓÒÚË ÍÓÌÒÚËÚÛÂÌÚ Â‰ËÌˈ˚ ̇ ÚÂı ̇·Ó‡ı, ̇ ÍÓÚÓ˚ı
ÙÛÌ͈Ëfl ‡‚̇ ‰ËÌˈÂ, Á‡ÏÂÌËÚ¸ ‚Ò ËÌ‚ÂÒÌ˚ Á̇˜ÂÌËfl
‡„ÛÏÂÌÚÓ‚ ‚ ÒÓÓÚ‚ÂÚÒÚ‚ËË Ò ‚˚‡ÊÂÌËÂÏ (3.2), ‡ÒÍ ˚Ú¸ ÒÍÓ·-
ÍË Ë ÔË‚ÂÒÚË ÔÓ‰Ó·Ì˚ ˜ÎÂÌ˚ ‚ ÒÓÓÚ‚ÂÚÒÚ‚ËÂ Ò ‚˚‡ÊÂÌËÂÏ
(3.5).
è Ë Ï Â 1 . á‡ÔËÒ‡Ú¸ ‚ ‚ˉ ÏÌÓ„Ó˜ÎÂ̇ ÙÛÌÍˆË˛ F(x
1
,
x
2
) = m
0
g m
1
g m
2
. àÒÔÓθÁÛfl ÒÓÓÚÌÓ¯ÂÌËfl (3.2) Ë (3.5), ÔÓ-
ÎÛ˜ËÏ
F(x
1
, x
2
) = (1 g x
1
)⋅(1 g x
2
) g (1 g x
1
)⋅x
2
g
g x
1
⋅(1 g x
2
) = 1 g x
1
g x
2
g x
1
⋅x
2
g x
2
g
g x
1
⋅x
2
g x
1
g x
1
⋅x
2
= 1 g x
1
⋅x
2
. ➤
íÂÓÂχ Ü„‡ÎÍË̇ ‰‡ÂÚ ËÌÛ˛ ÙÛÌ͈ËÓ̇θÌÓ ÔÓÎÌÛ˛ ÒËÒ-
ÚÂÏÛ ÙÛÌ͈ËÈ, ˜ÂÏ ÚÂÓÂχ “Ó ‰‚Ûı ÙÓχı ÙÛÌ͈ËÈ”, ÔÓ˝ÚÓÏÛ
ˆÂÎÂÒÓÓ·‡ÁÌÓ ‡ÒÒÏÓÚÂÚ¸ ‚ÓÔÓÒ Ó ÚÓÏ, ͇ÍËÏË Ò‚ÓÈÒÚ‚‡ÏË
‰ÓÎÊÌ˚ ӷ·‰‡Ú¸ ÙÛÌ͈ËË, ˜ÚÓ·˚ ÒÓÒÚ‡‚ËÚ¸ ÙÛÌ͈ËÓ̇θÌÓ
ÔÓÎÌÛ˛ ÒËÒÚÂÏÛ. ÑÎfl ˝ÚÓ„Ó ÌÛÊÌÓ Í·ÒÒËÙˈËÓ‚‡Ú¸ ·Û΂˚
ÙÛÌ͈ËË ÔÓ Ëı Ò‚ÓÈÒÚ‚‡Ï.
3.2. èüíú äãÄëëéÇ ÅìãÖÇõï îìçäñàâ
ëÛ˘ÂÒÚ‚ÛÂÚ ÔflÚ¸ Í·ÒÒÓ‚ ÙÛÌ͈ËÈ, ӷ·‰‡˛˘Ëı ÚÂÏ Ò‚ÓÈÒÚ-
‚ÓÏ, ˜ÚÓ Î˛·‡fl ·Û΂‡ ÙÛÌ͈Ëfl, ÔÓÎÛ˜ÂÌ̇fl Ò ÔÓÏÓ˘¸˛ ÓÔ ‡-
ˆËÈ ÒÛÔÂÔÓÁˈËË Ë ÔÓ‰ÒÚ‡ÌÓ‚ÍË ËÁ ÙÛÌ͈ËÈ ‰‡ÌÌÓ„Ó Í·ÒÒ‡,
·Û‰ÂÚ ÔË̇‰ÎÂʇڸ Í ˝ÚÓÏÛ Ê Í·ÒÒÛ.
ùÚÓ ÒÎÂ‰Û˛˘Ë ÔflÚ¸ Í·ÒÒÓ‚:

134
ÎËÌÂÈÌ˚ ÙÛÌ͈ËË,
ÙÛÌ͈ËË, ÒÓı‡Ìfl˛˘Ë ÌÛθ,
ÙÛÌ͈ËË, ÒÓı‡Ìfl˛˘Ë ‰ËÌˈÛ,
ÏÓÌÓÚÓÌÌ˚ ÙÛÌ͈ËË,
Ò‡ÏÓ‰‚ÓÈÒÚ‚ÂÌÌ˚ ÙÛÌ͈ËË.
é Ô Â ‰ Â Î Â Ì Ë Â. ÅÛ΂‡ ÙÛÌ͈Ëfl ̇Á˚‚‡ÂÚÒfl ÎËÌÂÈÌÓÈ, ÂÒ-
ÎË Ó̇ ÏÓÊÂÚ ·˚Ú¸ Á‡ÔË҇̇ ÔÓÎËÌÓÏÓÏ Ô‚ÓÈ ÒÚÂÔÂÌË:
F(x
1
, x
2
,..., x
n
) = a
0
g a
1
⋅x
1
g a
2
⋅x
2
g ... g a
n
x
n
,
Ú.Â. ‚ ‚ˉ ÓÚˈ‡ÌËfl ‡‚ÌÓÁ̇˜ÌÓÒÚË ‚ÒÂı ‡„ÛÏÂÌÚÓ‚ ÙÛÌÍ-
ˆËË, „‰Â ‡
0
, ‡
1
,..., a
n
– ÍÓ˝ ÙÙˈËÂÌÚ˚, ‡‚Ì˚ 0 ËÎË 1. åÓÊÌÓ
̇ÈÚË ÍÓ΢ÂÒÚ‚Ó ‡Á΢Ì˚ı ÎËÌÂÈÌ˚ı ÙÛÌ͈ËÈ n-‡„ÛÏÂÌÚÓ‚.
ÑÂÈÒÚ‚ËÚÂθÌÓ, ÂÒÎË Í‡Ê‰ÓÏÛ Ì‡·ÓÛ ÍÓ˝ÙÙˈËÂÌÚÓ‚ ‡
0
, ‡
1
,...,
a
n
ÔÓÒÚ‡‚ËÚ¸ ‚ ÒÓÓÚ‚ÂÚÒÚ‚Ë (n + 1) ‡Áfl‰ÌÓ ‰‚Ó˘ÌÓ ˜ËÒÎÓ,
ÚÓ ‚ÒÂ„Ó Ú‡ÍËı ˜ËÒÂÎ, ‡ ÒΉӂ‡ÚÂθÌÓ ÙÛÌ͈ËÈ, ·Û‰ÂÚ 2
n+1
.
Ç Í‡˜ÂÒÚ‚Â ÔËχ ‡ÒÒÏÓÚËÏ ‚Ò ÎËÌÂÈÌ˚ ÙÛÌ͈ËË Ó‰-
ÌÓ„Ó Ë ‰‚Ûı ‡„ÏÂÌÚÓ‚.
ãËÌÂÈÌ˚ı ÙÛÌ͈ËÈ Ó‰ÌÓ„Ó ‡„ÛÏÂÌÚ‡ ÏÓÊÂÚ ·˚Ú¸ ˜ÂÚ˚Â, ‡
Ú‡Í Í‡Í ÙÛÌ͈ËÈ Ó‰ÌÓ„Ó ‡„ÛÏÂÌÚ‡ ‚ÒÂ„Ó ˜ÂÚ˚Â, ÚÓ ‚Ò ÓÌË
ÎËÌÂÈÌ˚. ÑÂÈÒÚ‚ËÚÂθÌÓ:
F
0
(x) = x g x = 0,
F
1
(x) = 1 g
x = x,
F
2
(x) = 1 g x =
x ,
F
3
(x) = x g
x = 1.
îÛÌ͈Ëfl F
0
(ı), ‡‚̇fl ÌÛβ, ÏÓÊÂÚ ·˚Ú¸ ÔÓÎÛ˜Â̇ Í‡Í ÓÚ-
ˈ‡ÌË ‡‚ÌÓÁ̇˜ÌÓÒÚË ˜ÂÚÌÓ„Ó ˜ËÒ· ı ‚ ÒÓÓÚ‚ÂÚÒÚ‚ËË Ò ‚˚-
‡ÊÂÌËÂÏ (3.3).
îÛÌ͈Ëfl F
1
(x), ‡‚̇fl ı, ÏÓÊÂÚ ·˚Ú¸ ÔÓÎÛ˜Â̇ Í‡Í Â‰ËÌˈ‡
ÓÚˈ‡ÌËfl ‡‚ÌÓÁ̇˜ÌÓÒÚË ËÌ‚ÂÒÌÓ„Ó Á̇˜ÂÌËfl ı, ÎË·Ó ‚ ÒÓ-
ÓÚ‚ÂÚÒÚ‚ËË Ò ‚˚‡ÊÂÌËÂÏ (3.4), Í‡Í ÓÚˈ‡ÌË ‡‚ÌÓÁ̇˜ÌÓÒÚË
̘ÂÚÌÓ„Ó ˜ËÒ· ı.
îÛÌ͈Ëfl F
2
(ı), ‡‚̇fl ËÌ‚ÂÒÌÓÏÛ Á̇˜ÂÌ˲ ı, ÔÓÎÛ˜‡ÂÚÒfl
‚ ÒÓÓÚ‚ÂÚÒÚ‚ËË Ò ‚˚‡ÊÂÌËÂÏ (3.2).
ÑÎfl ÚÓ„Ó ˜ÚÓ·˚ ÔÓÎÛ˜ËÚ¸ ÙÛÌÍˆË˛ F
3
(ı), ‡‚ÌÛ˛ ‰ËÌˈÂ,
‰ÓÒÚ‡ÚÓ˜ÌÓ ‚ ÒÓÓÚ‚ÂÚÒÚ‚ËË Ò ‚˚‡ÊÂÌËÂÏ (3.2) Á‡ÔËÒ‡Ú¸ ËÌ-
‚ÂÒÌÓ Á̇˜ÂÌË ı ‚ ‚ˉÂ
x = 1 g x, Á‡ÚÂÏ ÔÓ‰ÒÚ‡‚Ë‚ Â„Ó ‚
‚˚‡ÊÂÌË ÙÛÌ͈ËË F
3
(x) = x g x g 1 = 0 g 1 = 1. á‰ÂÒ¸
‚̇˜‡Î ̇ ÓÒÌÓ‚‡ÌËË ‚˚‡ÊÂÌËfl (3.3) ÔÓÎÛ˜‡ÂÏ 0 g 1, ‡ Á‡-
ÚÂÏ Ì‡ ÓÒÌÓ‚‡ÌËË ‚˚‡ÊÂÌËfl (3.1)
ÏÓÊÌÓ
ÔÓÎÛ˜ËÚ¸
F
3
(x)
=
= 0 g 1 = 1.
ãËÌÂÈÌ˚ı ÙÛÌ͈ËÈ ‰‚Ûı ‡„ÛÏÂÌÚÓ‚ ‚ÓÒÂϸ. îÛÌ͈ËË ËÏÂ-
˛Ú ÌÓχ ‚ ÒÓÓÚ‚ÂÚÒÚ‚ËË Ò Ú‡·Î. 3.6:

135
F
0
(x, y) = x g x g y g y = 0,
F
3
(x, y) = x g y g y = x,
F
5
(x, y) = x g x g y = y,
F
6
(x, y) = x g y,
F
9
(x, y) = 1 g x g y = x ∼ y,
F
10
(x, y) = 1 g y g x g x =
y,
F
12
(x, y) = 1 g x g y g y =
x,
F
15
(x, y) = x g x g y g y g 1 = 1.
í Â Ó Â Ï ‡. èË ÒÛÔÂÔÓÁˈËË ÎËÌÂÈÌ˚ı ÙÛÌ͈ËÈ Ë ÔÓ‰-
ÒÚ‡ÌÓ‚Í ‚ ˝ÚË ÙÛÌ͈ËË ÔÂÂÏÂÌÌ˚ı ÔÓÎÛ˜‡˛ÚÒfl ÚÓθÍÓ ÎË-
ÌÂÈÌ˚ ÙÛÌ͈ËË.
Ñ Ó Í ‡ Á ‡ Ú Â Î ¸ Ò Ú ‚ Ó. ÑÂÈÒÚ‚ËÚÂθÌÓ, ÔÛÒÚ¸ Á‡‰‡Ì˚ ÎËÌÂÈ-
Ì˚ ÙÛÌ͈ËË:
F
1
= F
1
(x
1
, x
2
,..., x
n
) = ‡
0
g a
1
x
1
g a
2
x
2
g ... g a
n
x
n
,
ϕ
1
= ϕ
1
(y
1
, y
2
,..., y
m1
) = b
10
g b
11
y
1
g b
12
y
2
g ... g b
1m1
y
m1
,
ϕ
2
= ϕ
2
(y
1
, y
2
,..., y
m2
) = b
20
g b
21
y
1
g b
22
y
2
g ... g b
2m2
y
m2
,
............................................................................................
ϕ
i
= ϕ
i
(y
1
, y
2
,..., y
mi
) = b
i0
g b
i1
y
1
g b
i2
y
2
g ... g b
imi
y
mi
,
............................................................................................
ϕ
n
= ϕ
n
(y
1
, y
2
,..., y
mn
) = b
n0
g b
n1
y
1
g b
n2
y
2
g ... g b
nmn
y
mn
,
„‰Â a
i
Ë b
ij
– ÍÓ˝ÙÙˈËÂÌÚ˚, ‡‚Ì˚ ÌÛβ ËÎË Â‰ËÌˈÂ.
èÓ‰ÒÚ‡‚Ë‚ ϕ
i
‚ÏÂÒÚÓ ‡„ÛÏÂÌÚÓ‚ x
i
‚ ÙÛÌÍˆË˛ F
1
, ÔÓÎÛ˜ËÏ
ÙÛÌÍˆË˛, ‚ ÍÓÚÓÓÈ ÍÓ˝ÙÙˈËÂÌÚ˚ a
i
ÛÏÌÓʇ˛ÚÒfl ̇ ÎËÌÂÈ-
Ì˚ ÙÛÌ͈ËË ϕ
i
, ÔË ˝ÚÓÏ ÔÓÎÛ˜‡˛ÚÒfl ÎËÌÂÈÌ˚ ÙÛÌ͈ËË.
è˂‰fl ÔÓ‰Ó·Ì˚ ˜ÎÂÌ˚, ÔÓÎÛ˜ËÏ ÙÛÌÍˆË˛ F
2
‚ ‚ˉ ÔÓÎËÌÓ-
χ Ô‚ÓÈ ÒÚÂÔÂÌË.
è Ë Ï Â 1. èÛÒÚ¸ Á‡‰‡Ì˚ ÎËÌÂÈÌ˚ ÙÛÌ͈ËË
F
1
(x
1
, x
2
, x
3
) = x
1
g x
2
g x
3
,
ϕ
1
(y
1
, y
2
, y
3
) = y
1
g y
2
g y
3
,
ϕ
2
(y
2
, y
3
, y
4
) = 1 g y
2
g y
3
g y
4
,
ϕ
3
(y
2
, y
3
, y
4
) = y
2
g y
3
g y
4
.
í·ÛÂÚÒfl ÔÓ͇Á‡Ú¸, ˜ÚÓ ÙÛÌ͈Ëfl F
2
(ϕ
1
, ϕ
2
, ϕ
3
) ÎËÌÂÈ̇fl.
136
ê  ¯ Â Ì Ë Â. èÓ‰ÒÚ‡‚ËÏ ‚ÏÂÒÚÓ ı
1
, ı
2
, ı
3
ÙÛÌ͈ËË ϕ
1
, ϕ
2
, ϕ
3
,
ÔÓÎÛ˜ËÏ F
2
(y
1
, y
2
, y
3
, y
4
) = y
1
g y
2
g y
3
g 1 g y
2
g y
3
g
y
4
g
g y
2
g y
3
g y
4
. è˂‰fl ÔÓ‰Ó·Ì˚ ˜ÎÂÌ˚ , ÔÓÎÛ˜ËÏ
F
2
(y
1
, y
2
, y
3
, y
4
) = 1 g y
1
g y
2
g y
3
.
îÛÌ͈Ëfl F
2
(y
1
, y
2
, y
3
, y
4
) – ÎËÌÂÈ̇fl.
èË ÔÓ‰ÒÚ‡ÌÓ‚Í ÔÂÂÏÂÌÌ˚ı ÙÛÌ͈Ëfl Ú‡ÍÊ ÓÒÚ‡ÂÚÒfl ÎË-
ÌÂÈÌÓÈ. á‡ÏÂÌË‚, ̇ÔËÏÂ, ‚ ÔÓÒΉÌÂÏ ‚˚‡ÊÂÌËË ÔÂÂ-
ÏÂÌÌ˚Â y
1
, y
2
, y
3
̇ ı
1
, ı
2
, ı
3
, ÔÓÎÛ˜ËÏ Ú‡ÍÊ ÎËÌÂÈÌÛ˛ ÙÛÌÍ-
ˆË˛. ➤
ë Î Â ‰ Ò Ú ‚ Ë Â. îÛÌ͈ËÓ̇θÌÓ ÔÓÎ̇fl ÒËÒÚÂχ ‰ÓÎÊ̇ ÒÓ-
‰Âʇڸ ıÓÚfl ·˚ Ó‰ÌÛ ÌÂÎËÌÂÈÌÛ˛ ÙÛÌÍˆË˛, Ú.Â. ÂÒÎË ÒËÒÚÂχ
ÒÓ‰ÂÊËÚ ÚÓθÍÓ ÎËÌÂÈÌ˚ ÙÛÌ͈ËË, ÚÓ ‚ ÒÓÓÚ‚ÂÚÒÚ‚ËË Ò ‰Ó͇-
Á‡ÌÌÓÈ ‚˚¯Â ÚÂÓÂÏÓÈ, ËÏÂfl ÚÓθÍÓ ÎËÌÂÈÌ˚ ÙÛÌ͈ËË, ÌÂθ-
Áfl ÔÓÎÛ˜ËÚ¸ ÌÂÎËÌÂÈÌÛ˛.
ç‡ÔÓÚË‚, Ú‡ÍÓ ÛÚ‚ÂʉÂÌË ‰Îfl ÌÂÎËÌÂÈÌ˚ı ÙÛÌ͈ËÈ ÌÂ-
‚ÂÌÓ.
ëΉÛÂÚ ÓÚÏÂÚËÚ¸, ˜ÚÓ ÌÂθÁfl ÔÓÎÛ˜ËÚ¸ ÙÛÌ͈ËÓ̇θÌÓ
ÔÓÎÌÛ˛ ÒËÒÚÂÏÛ ËÁ ÙÛÌ͈ËÈ Ó‰ÌÓ„Ó ‡„ÛÏÂÌÚ‡, Ú‡Í Í‡Í ‚Ò ÓÌË
ÎËÌÂÈÌ˚.
ÅÛ΂˚ ÙÛÌ͈ËË, ÒÓı‡Ìfl˛˘Ë ÌÛθ. é Ô Â ‰ Â Î Â Ì Ë Â.
îÛÌ͈ËÂÈ, ÒÓı‡Ìfl˛˘ÂÈ ÌÛθ, ̇Á˚‚‡˛ Ú Ú‡ÍÛ˛, ÍÓÚÓ‡fl ‡‚̇
ÌÛβ ̇ ÌÛ΂ÓÏ Ì‡·Ó ‡„ÛÏÂÌÚÓ‚.
í Â Ó Â Ï ‡. èË ÒÛÔÂÔÓÁˈËË ÙÛÌ͈ËÈ, ÒÓı‡Ìfl˛˘Ëı
ÌÛθ, Ë ÔÓ‰ÒÚ‡ÌÓ‚Í ‚ ˝ÚË ÙÛÌ͈ËË ÔÂÂÏÂÌÌ˚ı ÔÓÎÛ˜‡˛ÚÒfl
ÚÓθÍÓ ÙÛÌ͈ËË, ÒÓı‡Ìfl˛˘Ë ÌÛθ.
Ñ Ó Í ‡ Á ‡ Ú Â Î ¸ Ò Ú ‚ Ó. èÛÒÚ¸ Á‡‰‡Ì˚ ÙÛÌ͈ËË, ÒÓı‡Ìfl˛˘ËÂ
ÌÛθ:
FFxx x
n1112
= (, , ), ...,
ϕϕ
1112 1
= (, , ),yy y
m
...,
ϕϕ
2212 2
= (, , ),yy y
m
...,
.................................,
ϕϕ
2212 2
= (, , ),yy y
m
...,
................................,
ϕϕ
nn mn
yy y= (, , ).
12
...,
èÓ‰ÒÚ‡‚Ë‚ ÙÛÌ͈ËË ϕ
i
‚ ‚˚‡ÊÂÌË F
1
‚ÏÂÒÚÓ x
i
, ÔÓÎÛ˜ËÏ
ÙÛÌÍˆË˛ F
2
:
137
Fy y y F
mk n21 2 11 2
(, , ) (, , ). ..., ..., = ϕϕ ϕ
í‡Í Í‡Í Í‡Ê‰‡fl ÙÛÌ͈Ëfl ϕ
i
ÒÓı‡ÌflÂÚ ÌÛθ, Ú.Â. ‡‚̇ ÌÛβ
̇ ÌÛ΂ÓÏ Ì‡·ÓÂ, ÚÓ Ë ÙÛÌ͈Ëfl F
2
Ú‡ÍÊ ÒÓı ‡ÌflÂÚ ÌÛθ ̇
ÌÛ΂ÓÏ Ì‡·ÓÂ
(
,,
)
yy y
mk12
...,
.
é˜Â‚ˉÌÓ, ˜ÚÓ Î˛·‡fl ÔÓ‰ÒÚ‡Ìӂ͇ ‡„ÛÏÂÌÚÓ‚ Ì ÏÓÊÂÚ
ËÁÏÂÌËÚ¸ Á̇˜ÂÌË ÙÛÌ͈ËË, Ú‡Í Í‡Í Ì‡ ÌÛ΂ÓÏ Ì‡·ÓÂ
‚Ò ‡„ÛÏÂÌÚ˚ ‡‚Ì˚ ÌÛβ, Á̇˜ËÚ Ë ÙÛÌ͈Ëfl ÒÓı ‡ÌflÂÚ
ÌÛθ.
è Ë Ï Â 2. èÛÒÚ¸ Á‡‰‡Ì˚ ÙÛÌ͈ËË, ÒÓı‡Ìfl˛˘Ë ÌÛθ,
Fx x x x x x x
11 2 3 1 2 2 3
(, , ) , = ⋅∨⋅
ϕ
11 3 1 3
(
,
)
,yy yy
= ⋅
ϕ
21 2 1 2
(, ) ,yy yy = ⋅
ϕ
31 2 1 2
(, ) .yy yy = ⋅
ê Â ¯ Â Ì Ë Â.
èÓ‰ÒÚ‡‚Ë‚ ÙÛÌ͈ËË
yy
12 3
,,
ϕ ‚ ‚˚‡ÊÂÌË F
1
, ÔÓÎÛ˜ËÏ
Fy y y y y y y y y y
21 2 3 1 3 2 2 2
(,,)()()()() ϕ = ⋅⋅⋅∨⋅⋅⋅ =
111
= ⋅⋅∨∨∨⋅⋅= ⋅∨⋅()()()() .yy y y y y yy yy yy
11 1 1 1132 2232
Ç ÂÁÛθڇÚ ӷ‡ÁÓ‚‡Ì‡ ÙÛÌ͈Ëfl F
2
, Ú‡ÍÊ ÒÓı‡Ìfl˛˘‡fl
ÌÛθ ̇ ÌÛ΂ÓÏ Ì‡·ÓÂ.
èÓ‰ÒÚ‡‚Ë‚ ‚ÏÂÒÚÓ ÔÂÂÏÂÌÌ˚ı y
1
, y
2
, y
3
‰Û„ËÂ ÔÂÂÏÂÌÌ˚Â,
ÏÓÊÌÓ Û·Â‰ËÚ¸Òfl, ˜ÚÓ ÙÛÌ͈Ëfl F
2
·Û‰ÂÚ Ú‡ÍÊ ÒÓı‡Ìfl˛˘ÂÈ
ÌÛθ. ➤
ë Î Â ‰ Ò Ú ‚ Ë Â. Ç ÙÛÌ͈ËÓ̇θÌÓ ÔÓÎÌÓÈ ÒËÒÚÂÏ ‰ÓÎÊ̇ ÒÓ-
‰ÂʇڸÒfl ıÓÚfl ·˚ Ӊ̇ ÙÛÌ͈Ëfl, Ì ÒÓı‡Ìfl˛˘‡fl ÌÛθ, Ú.Â.
‡‚̇fl ‰ËÌˈ ̇ ÌÛ΂ÓÏ Ì‡·ÓÂ.
ÑÂÈÒÚ‚ËÚÂθÌÓ, ÂÒÎË ÒËÒÚÂχ ÒÓ‰ÂÊËÚ ÚÓθÍÓ ÙÛÌ͈ËË,
ÒÓı‡Ìfl˛˘Ë ÌÛθ, ÚÓ, ‚ ÒÓÓÚ‚ÂÚÒÚ‚ËË Ò ÚÂÓÂÏÓÈ, ÌÂθÁfl ÔÓ-
ÎÛ˜ËÚ¸ ‚ ˝ÚÓÈ ÒËÒÚÂÏ ÙÛÌÍˆË˛, Ì ÒÓı‡Ìfl˛˘Û˛ ÌÛθ.
ÅÛ΂˚ ÙÛÌ͈ËË, ÒÓı ‡Ìfl˛˘Ë ‰ËÌˈÛ. é Ô Â ‰ Â Î Â Ì Ë Â.
îÛÌ͈ËÂÈ, ÒÓı‡Ìfl˛˘ÂÈ Â‰ËÌˈÛ, ̇Á˚ ‚‡˛Ú Ú‡ÍÛ˛, ÍÓÚÓ‡fl
‡‚̇ ‰ËÌˈ ̇ ‰ËÌ˘ÌÓÏ Ì‡·Ó ‡„ÛÏÂÌÚÓ‚ (1, 1,..., 1).
í Â Ó Â Ï ‡. èË ÒÛÔÂÔÓÁˈËË ÙÛÌ͈ËÈ, ÒÓı‡Ìfl˛˘Ëı ‰Ë-
ÌˈÛ, Ë ÔÓ‰ÒÚ‡ÌÓ‚Í ‚ ˝ÚË ÙÛÌ͈ËË Ô ÂÏÂÌÌ˚ı ÔÓÎÛ˜‡˛ÚÒfl
ÚÓθÍÓ ÙÛÌ͈ËË, ÒÓı‡Ìfl˛˘Ë ‰ËÌˈÛ.
ÑÓ͇Á‡ÚÂθÒÚ‚Ó ÚÂÓÂÏ˚ ‡Ì‡Îӄ˘ÌÓ ‰Ó͇Á‡ÚÂθÒÚ‚Û Ô‰˚-
‰Û˘ÂÈ.
