Овчаров Л.А. и др. Математические модели информационых процессов и управления

Подождите немного. Документ загружается.

118

Ñ Ó Í ‡ Á ‡ Ú Â Î ¸ Ò Ú ‚ Ó:

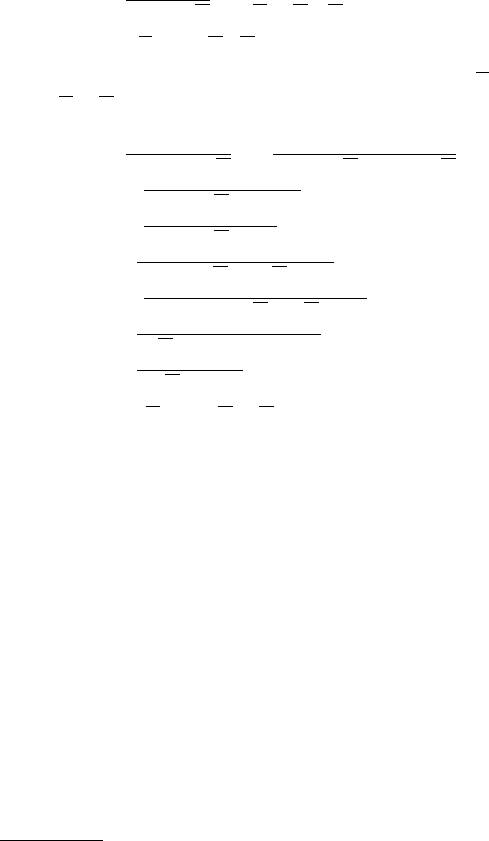
()()()AC BC A C B C⋅∨⋅ = ∨∨= [ÚÂÓÂÏ‡ 5‡, 5·]

= ⋅∨ ⋅AC BC. [ÚÂÓÂÏ‡ 7]

8·. íÂ·ÛÂÚÒﬂ ‰ÓÍ‡Á‡Ú¸, ˜ÚÓ

()()ACBC∨∨=

()AC∨ ×

× ∨().BC

Ñ Ó Í ‡ Á ‡ Ú Â Î ¸ Ò Ú ‚ Ó:

()( )( )AC BC ABAC BCCC∨∨= ⋅∨⋅∨⋅∨⋅ = [4·]

= ⋅∨⋅∨⋅∨ =()AB AC BC 0 [5]

= ⋅∨⋅∨⋅ =()AB AC BC [2a]

= ⋅⋅ ∨ ∨⋅ ∨⋅ =AB C C AC BC( ) [2·, 5]

= ⋅⋅∨⋅⋅∨⋅∨⋅ =()ABC ABC AC BC [4·]

= ⋅∨∨⋅⋅∨=AC B BC A() ()11 [4·]

= ⋅∨⋅ =()()AC BC [ÚÂÓÂÏ‡ 2‡]

= ∨∨()( ).ACBC [ÚÂÓÂÏ‡ 5‡, 5·]

ùÚË ÚÂÓÂÏ˚ ·Û‰ÛÚ ‚ ‰‡Î¸ÌÂÈ¯ÂÏ ÌÂÓ·ıÓ‰ËÏ˚ ÔË ÔÂÓ·‡-

ÁÓ‚‡ÌËË ÎÓ„Ë˜ÂÒÍËı ‚˚‡ÊÂÌËÈ.

ÅÛÎÂ‚˚ ÙÛÌÍˆËË. îÛÌÍˆËﬂ F(x

, x

,..., x

) Ì‡Á˚‚‡ÂÚÒﬂ ·Û-

ÎÂ‚ÓÈ

∗

, ÂÒÎË ÓÌ‡ Ú‡Í ÊÂ, Í‡Í Ë ÂÂ ‡„ÛÏÂÌÚ˚, ÏÓÊÂÚ ÔËÌËÏ‡Ú¸

ÚÓÎ¸ÍÓ ‰‚‡ ÁÌ‡˜ÂÌËﬂ: 0 ËÎË 1. èÓ˝ÚÓÏÛ Î˛·‡ﬂ ·ÛÎÂ‚‡ ÙÛÌÍˆËﬂ

ÏÓÊÂÚ ·˚Ú¸ Á‡‰‡Ì‡ Ú‡·ÎËˆÂÈ ÂÂ ÁÌ‡˜ÂÌËÈ ‚ Á‡‚ËÒËÏÓÒÚË ÓÚ

ÁÌ‡˜ÂÌËÈ ‡„ÛÏÂÌÚÓ‚.

ç‡ÔËÏÂ, ÙÛÌÍˆËﬂ F(x

, x

), Á‡‰‡ÌÌ‡ﬂ Ú‡·ÎËˆÂÈ 3.4,

ÓÔÂ‰ÂÎÂÌ‡ Ì‡ ‚ÓÒ¸ÏË Ì‡·Ó‡ı. ç‡·ÓÓÏ Ì‡Á˚‚‡˛ Ú ÒÓ‚ÓÍÛÔ-

ÌÓÒÚ¸ ÁÌ‡˜ÂÌËÈ ‡„ÛÏÂÌÚÓ‚ ÙÛÌÍˆËË. îÛÌÍˆËﬂ, Á‡‰‡ÌÌ‡ﬂ Ú‡·-

ÎËˆÂÈ, ÔËÌËÏ‡ÂÚ ÁÌ‡˜ÂÌËÂ, ‡‚ÌÓÂ Â‰ËÌËˆÂ, Ì‡ Ì‡·Ó‡ı

(0,0,0; 0,1,0; 0,1,1; 1,1,0), Ì‡ ÓÒÚ‡Î¸Ì˚ı Ì‡·Ó‡ı ÙÛÌÍˆËﬂ ‡‚Ì‡

ÌÛÎ˛.

èË‚Â‰ÂÌÌ‡ﬂ ÙÛÌÍˆËﬂ ÓÔÂ‰ÂÎÂÌ‡ Ì‡ ‚ÒÂı Ì‡·Ó‡ı ‡„ÛÏÂÌ-

ÚÓ‚. îÛÌÍˆËﬂ, ÍÓÚÓ‡ﬂ ÓÔÂ‰ÂÎÂÌ‡ Ì‡ ‚ÒÂı Ì‡·Ó‡ı, Ì‡Á˚‚‡ÂÚ-

Òﬂ ÔÓÎÌÓÒÚ¸˛ ÓÔÂ‰ÂÎÂÌÌÓÈ.

ë‚ÓÈÒÚ‚‡ ·ÛÎÂ‚˚ı ÙÛÌÍˆËÈ. 1. ã˛·‡ﬂ ·ÛÎÂ‚‡ ÙÛÌÍˆËﬂ

∗

ÑÊÓ‰Ê ÅÛÎ¸ Ó‰ËÎÒﬂ 2 ÌÓﬂ·ﬂ 1815 „Ó‰‡ ‚ ÓÍÂÒÚÌÓÒÚﬂı É. ãËÌÍÓÎ¸Ì‡ ‚

ÒÂÏ¸Â ÙÂÏÂÓ‚. Ç 1849 „Ó‰Û ÅÛÎ¸ ÔÓÎÛ˜‡ÂÚ ‰ÓÎÊÌÓÒÚ¸ ÔÓÙÂÒÒÓ‡ ‚ äÛËÌÁ –

ÍÓÎÎÂ‰ÊÂ „. äÓÍÂ (àÎ‡Ì‰Ëﬂ). äÓÏÂ ‡·ÓÚ ÔÓ ÎÓ„ËÍÂ ËÁ‚ÂÒÚÂÌ Ò‚ÓËÏË ‡Á-

‡·ÓÚÍ‡ÏË ‚ ÚÂÓËË ‚ÂÓﬂÚÌÓÒÚÂÈ. èË¯ÂÎ Í ‚˚‚Ó‰Û, ˜ÚÓ ÎÓ„ËÍ‡ ÌÂÁ‡‚ËÒËÏ‡ ÓÚ

Ï‡ÚÂÏ‡ÚËÍË Ë ‰ÓÎÊÌ‡ ÒÓÒÚ‡‚ËÚ¸ ÂÂ ÓÒÌÓ‚Û.

119

n-‡„ÛÏÂÌÚÓ‚ ÓÔÂ‰ÂÎÂÌ‡ Ì‡ 2

Ì‡·Ó‡ı (2

 ‡ÁÎË˜Ì˚ı ÁÌ‡˜Â-

ÌËÈ ÂÂ ‡„ÛÏÂÌÚÓ‚).

ÑÂÈÒÚ‚ËÚÂÎ¸ÌÓ, Ú‡Í Í‡Í Í‡Ê‰ÓÏÛ Ì‡·ÓÛ ÏÓÊÌÓ ÔÓÒÚ‡‚ËÚ¸ ‚

ÒÓÓÚ‚ÂÚÒÚ‚ËÂ n-‡Áﬂ‰ÌÓÂ ‰‚ÓË˜ÌÓÂ ˜ËÒÎÓ, ÚÓ ÍÓÎË˜ÂÒÚ‚Ó ‡Á-

ÎË˜Ì˚ı n-‡Áﬂ‰Ì˚ı ˜ËÒÂÎ, ‡ ÒÎÂ‰Ó‚‡ÚÂÎ¸ÌÓ, Ë Ì‡·ÓÓ‚ ‡‚-

ÌÓ 2

ç‡ÔËÏÂ, ‡ÒÒÏÓÚÂÌÌ‡ﬂ ÙÛÌÍˆËﬂ ÚÂı ‡„ÛÏÂÌÚÓ‚ (Ú‡·Î.

3.4) ÓÔÂ‰ÂÎÂÌ‡ Ì‡ ‚ÓÒ¸ÏË Ì‡·Ó‡ı. ÑÎﬂ ÔÓÒÚÓÚ˚ ‚ ‰‡Î¸ÌÂÈ-

¯ÂÏ Í‡Ê‰ÓÏÛ Ì‡·ÓÛ ÔÂÂÏÂÌÌ˚ı ·Û‰ÂÚ ÒÚ‡‚ËÚ¸Òﬂ ‚ ÒÓÓÚ‚ÂÚÒÚ-

‚ËÂ ÌÓÏÂ, ‡‚Ì˚È ‰‚ÓË˜ÌÓÏÛ ˜ËÒÎÛ:

0,0,0,..., 0 – ÌÛÎÂ‚ÓÈ Ì‡·Ó;

0,0,0,..., 1 – ÔÂ‚˚È Ì‡·Ó Ë Ú‡Í ‰‡ÎÂÂ.

2. óËÒÎÓ ‡ÁÎË˜Ì˚ı ·ÛÎÂ‚˚ı ÙÛÌÍˆËÈ n-‡„ÛÏÂÌÚÓ‚ ÍÓÌÂ˜ÌÓ

Ë ‡‚ÌÓ

ÑÂÈÒÚ‚ËÚÂÎ¸ÌÓ, Ú‡Í Í‡Í Î˛·‡ﬂ ·ÛÎÂ‚‡ ÙÛÌÍˆËﬂ n-‡„ÛÏÂÌÚÓ‚

ÓÔÂ‰ÂÎÂÌ‡ Ì‡ 2

Ì‡·Ó‡ı, Ì‡ ÍÓÚÓ˚ı ÓÌ‡ ÏÓÊÂÚ ÔËÌËÏ‡Ú¸

ÁÌ‡˜ÂÌËﬂ 0 ËÎË 1, ÚÓ ‚ ÒÓÓÚ‚ÂÚÒÚ‚ËÂ Î˛·ÓÈ ÙÛÌÍˆËË ÏÓÊÂÚ

·˚Ú¸ ÔÓÒÚ‡‚ÎÂÌÓ 2

-‡Áﬂ‰ÌÓÂ ‰‚ÓË˜ÌÓÂ ˜ËÒÎÓ; ‚ÒÂ„Ó Ú‡ÍËı ˜Ë-

ÒÂÎ, ‡ ÒÎÂ‰Ó‚‡ÚÂÎ¸ÌÓ, Ë ÙÛÌÍˆËÈ, ·Û‰ÂÚ

. Ç Í‡˜ÂÒÚ‚Â ÔËÏÂ-

‡ ‡ÒÒÏÓÚËÏ ÙÛÌÍˆËË Ó‰ÌÓ„Ó Ë ‰‚Ûı ‡„ÛÏÂÌÚÓ‚. ùÚË ÙÛÌÍ-

ˆËË ‚ ‡Î„Â·Â ÎÓ„ËÍË ËÏÂ˛Ú ÓÒÓ·ÓÂ ÁÌ‡˜ÂÌËÂ, ÔÓ˝ÚÓÏÛ Ëı ˜‡ÒÚÓ

Ì‡Á˚‚‡˛Ú ·‡ÁÓ‚˚ÏË. ëÛ˘ÂÒÚ‚Û˛Ú ˜ÂÚ˚Â ‡ÁÎË˜Ì˚ Â ÙÛÌÍˆËË

Ó‰ÌÓ„Ó ‡„ÛÏÂÌÚ‡ (Ú‡·Î. 3.5).

îÛÌÍˆËﬂ F

(ı) ÚÓÊ‰ÂÒÚ‚ÂÌÌÓ ‡‚Ì‡ ÌÛÎ˛, ÂÂ Ì‡Á˚‚‡˛Ú

ÍÓÌÒÚ‡ÌÚÓÈ ÌÛÎ¸ Ë Ó·ÓÁÌ‡˜‡˛Ú F

(ı) = 0. îÛÌÍˆËﬂ F

(ı)

ÚÓÊ‰ÂÒÚ‚ÂÌÌÓ ‡‚Ì‡ 1, ÂÂ Ì‡Á˚‚‡˛Ú ÍÓÌÒÚ‡ÌÚÓÈ Â‰ËÌËˆ‡ Ë

Ó·ÓÁÌ‡˜‡˛Ú F

(ı) = 1. îÛÌÍˆË˛ F

(ı), ÍÓÚÓ‡ﬂ ÔÓ‚ÚÓﬂÂÚ ÁÌ‡-

˜ÂÌËÂ ‡„ÛÏÂÌÚ‡ ı, Ó·ÓÁÌ‡˜‡˛Ú F

(ı) = ı Ë Ì‡Á˚‚‡˛Ú ÔÂÂ-

ÏÂÌÌ‡ﬂ ı. îÛÌÍˆË˛ F

(ı), ÔËÌËÏ‡˛˘Û˛ ÔÓÚË‚ÓÔÓÎÓÊÌ˚Â

ÁÌ‡˜ÂÌËﬂ ‡„ÛÏÂÌÚ‡ ı, Ó·ÓÁÌ‡˜‡˛Ú

Fx x

()= Ë Ì‡Á˚‚‡˛Ú ËÌ-

‚ÂÒËÂÈ ı.

àÌÓ„‰‡ ˝ÚË ˜ÂÚ˚Â ÙÛÌÍˆËË Ì‡Á˚‚‡˛Ú ÚË‚Ë‡Î¸Ì˚ÏË.

í‡·ÎËˆ‡ 3.4 í‡·ÎËˆ‡ 3.5

îÛÌÍˆËË Ó‰ÌÓ„Ó ‡„ÛÏÂÌÚ‡

0001 ìÒÎÓ‚ÌÓÂ ç‡Á‚‡ÌËÂ

001 0 X 0 1 Ó·ÓÁÌ‡˜Â- ÙÛÌÍˆËË

0 1 0 1

ÌËÂ

0 111 F

(x) 0 0 0 äÓÌÒÚ‡ÌÚ‡ ÌÛÎ¸

1 000 F

(x)0 1 ı èÂÂÏÂÌÌ‡ﬂ ı

1 0 1 0 F

(x) 1 0 ı àÌ‚ÂÒËﬂ ı

110 1 F

(x) 11 1 äÓÌÒÚ‡ÌÚ‡

1110 Â‰ËÌËˆ‡

120

ê‡ÒÒÏÓÚËÏ ÙÛÌÍˆËË ‰‚Ûı ‡„ÛÏÂÌÚÓ‚. ëÛ˘ÂÒÚ‚ÛÂÚ ¯ÂÒÚ-

Ì‡‰ˆ‡Ú¸ ‡ÁÎË˜Ì˚ı ÙÛÌÍˆËÈ ‰‚Ûı ‡„ÛÏÂÌÚÓ‚, ÓÌË ÔË‚Â‰ÂÌ˚

‚ Ú‡·Î. 3.6. Ç Ú‡·Î. 3.6 ËÏÂ˛ÚÒﬂ ÛÊÂ ËÁ‚ÂÒÚÌ˚Â ÙÛÌÍˆËË, ˝ÚÓ

– ÍÓÌÒÚ‡ÌÚ‡ ÌÛÎ¸, F

– ÍÓÌ˙˛ÌÍˆËﬂ, F

Ë F

– ÔÂÂÏÂÌÌ‡ﬂ ı

Ë ÔÂÂÏÂÌÌ‡ﬂ y, F

– ‰ËÁ˙˛ÌÍˆËﬂ, F

Ë F

– ËÌ‚ÂÒËﬂ y Ë

ËÌ‚ÂÒËﬂ ı, F

– ÍÓÌÒÚ‡ÌÚ‡ Â‰ËÌËˆ‡.

àÏÂ˛ÚÒﬂ Ë ÌÓ‚˚Â ÙÛÌÍˆËË. ê‡ÒÒÏÓÚËÏ Ëı. îÛÌÍˆËﬂ F

Á‡-

ÔÂÚ‡ ÔÓ y ‡‚Ì‡ 1, ÍÓ„‰‡ ‡„ÛÏÂÌÚ ı ‡‚ÂÌ 1 Ë ‡„ÛÏÂÌÚ y ‡-

‚ÂÌ 0; ˝Ú‡ ÙÛÌÍˆËﬂ ‡‚Ì‡ 0, ÍÓ„‰‡ ‡„ÛÏÂÌÚ ı ‡‚ÂÌ 1 Ë ‡„Û-

ÏÂÌÚ y ‡‚ÂÌ Ú‡ÍÊÂ 1. îÓÏ‡Î¸ÌÓ ÙÛÌÍˆËﬂ Á‡ÔËÒ˚‚‡ÂÚÒﬂ Ú‡Í:

Fx y x y

(, ) .= ⋅ èÓ‰ÒÚ‡‚Ë‚ ‡ÁÎË˜Ì˚Â ÁÌ‡˜ÂÌËﬂ ı Ë y ‚ ˝ÚÓ

‚˚‡ÊÂÌËÂ, ÏÓÊÌÓ Û·Â‰ËÚ¸Òﬂ ‚ Â„Ó ÒÔ‡‚Â‰ÎË‚ÓÒÚË.

ÄÌ‡ÎÓ„Ë˜ÌÓ ËÌÚÂÔÂÚËÛÂÚÒﬂ Ë ÙÛÌÍˆËﬂ Á‡ÔÂÚ‡ ÔÓ

xFxy yx:(,) .

= ⋅ îÛÌÍˆËﬂ F

(‡‚ÌÓÁÌ‡˜ÌÓÒÚ¸ ËÎË ˝Í‚Ë‚‡-

ÎÂÌÚÌÓÒÚ¸) ‡‚Ì‡ 1, ÂÒÎË ÁÌ‡˜ÂÌËﬂ ÂÂ ‡„ÛÏÂÌÚÓ‚ ÒÓ‚Ô‡‰‡˛Ú.

àÌ‚ÂÒÌ‡ﬂ ÂÈ ÙÛÌÍˆËﬂ Ì‡Á˚‚‡ÂÚÒﬂ ÌÂ‡‚ÌÓÁÌ‡˜ÌÓÒÚ¸˛ ËÎË

ÒÛÏÏÓÈ ÔÓ ÏÓ‰ÛÎ˛ ‰‚‡. ÑÎﬂ Ó·ÓÁÌ‡˜ÂÌËﬂ ÂÂ ËÌÓ„‰‡ ËÒÔÓÎ¸ÁÛÂÚ-

Òﬂ, ÍÓÏÂ ÔË‚Â‰ÂÌÌÓ„Ó, ÒËÏ‚ÓÎ ⊕.

ÑÎﬂ ˝ÚÓÈ ÙÛÌÍˆËË ı‡‡ÍÚÂÌ˚ ÒÎÂ‰Û˛˘ËÂ ÒÓÓÚÌÓ¯ÂÌËﬂ:

ı ÓÚËˆ‡ÌËÂ ‡‚ÌÓÁÌ‡˜ÌÓÒÚË ÌÛÎ¸ ‡‚ÌÓ ı

x g 0 = x, (3.1)

í‡·ÎËˆ‡ 3.6

îÛÌÍˆËË ‰‚Ûı ‡„ÛÏÂÌÚÓ‚

ı 0011ìÒÎÓ‚Ì˚Â ç‡Á‚‡ÌËÂ ÙÛÌÍˆËË

y 0 1 0 1 Ó·ÓÁÌ‡˜ÂÌËﬂ

(x, y) 0 0 0 0 0 äÓÌÒÚ‡ÌÚ‡ ÌÛÎ¸

(x, y)0001 x⋅y äÓÌ˙˛ÌÍˆËﬂ x, y

(x, y)001 0

xy⋅ îÛÌÍˆËﬂ Á‡ÔÂÚ‡ ÔÓ y

(x, y)0011 x èÂÂÏÂÌÌ‡ﬂ ı

(x, y)01 00

yx⋅ îÛÌÍˆËﬂ Á‡ÔÂÚ‡ ÔÓ ı

(x, y)01 0 1 y èÂÂÏÂÌÌ‡ﬂ y

(x, y)011 0 x g y çÂ‡‚ÌÓÁÌ‡˜ÌÓÒÚ¸

(x, y)011 1 ı ∨ y ÑËÁ˙˛ÌÍˆËﬂ x, y

(x, y) 1 00 0 x ↓ y îÛÌÍˆËﬂ èËÒ‡

(ÒÚÂÎÍ‡ èËÒ‡)

(x, y) 1 00 1 x ∼ y ê‡‚ÌÓÁÌ‡˜ÌÓÒÚ¸ (˝Í-

‚Ë‚‡ÎÂÌÚÌÓÒÚ¸)

(x, y) 1 0 1 0

àÌ‚ÂÒËﬂ y

(x, y) 1 0 11 y → x àÏÔÎËÍ‡ˆËﬂ ÓÚ y Í ı

(x, y) 1100

àÌ‚ÂÒËﬂ ı

(x, y) 110 1 ı → y àÏÔÎËÍ‡ˆËﬂ ÓÚ ı Í y

(x, y) 1110 x|y îÛÌÍˆËﬂ òÂÙÙÂ‡

(¯ÚËı òÂÙÙÂ‡)

(x, y) 1111 1 äÓÌÒÚ‡ÌÚ‡ Â‰ËÌËˆ‡

121

ı ÓÚËˆ‡ÌËÂ ‡‚ÌÓÁÌ‡˜ÌÓÒÚË 1 ‡‚ÌÓ ËÌ‚ÂÒÌÓÏÛ ÁÌ‡˜ÂÌË˛

x γ 1 =

x, (3.2)

ı ÓÚËˆ‡ÌËÂ ‡‚ÌÓÁÌ‡˜ÌÓÒÚË ı ‡‚ÌÓ ÌÛÎ˛

x g x = 0, (3.3)

ÓÚËˆ‡ÌËÂ ‡‚ÌÓÁÌ‡˜ÌÓÒÚË ÌÂ˜ÂÚÌÓ„Ó ˜ËÒÎ‡ ı ‡‚ÌÓ ı

x g x g x = x. (3.4)

Ç˚‡ÊÂÌËﬂ (3.3) Ë (3.4) ÏÓ„ÛÚ ·˚ Ú¸ Á‡ÔËÒ‡Ì˚ ‚ ·ÓÎÂÂ Ó·-

˘ÂÏ ‚Ë‰Â (3.5):

x g x g ... g x =

ÂÒÎË ÍÓÎË˜ÂÒÚ‚Ó – ÌÂ˜ÂÚÌÓÂ

ÂÒÎË ÍÓÎË˜ÂÒÚ‚Ó – ˜ÂÚÌÓÂ,







(3.5)

x g y = y g x. (3.6)

ùÚË ÒÓÓÚÌÓ¯ÂÌËﬂ ‚˚ÚÂÍ‡˛Ú ËÁ Ú‡·Î. 3.6.

àÏÔÎËÍ‡ˆËﬂ (F

Ë F

) – ˝ÚÓ ÙÛÌÍˆËﬂ, Ó·˙Â‰ËÌﬂ˛˘‡ﬂ ‰‚‡

‚˚ÒÍ‡Á˚‚‡ÌËﬂ, ÔË˜ÂÏ ÂÒÎË ËÏÔÎËÍ‡ˆËﬂ F

(ı, y) = x → y, ÚÓ

‚˚ÒÍ‡Á˚‚‡ÌËÂ ı Ì‡Á˚‚‡ÂÚÒﬂ ÔÓÒ˚ÎÍÓÈ, ‡ Û – ÒÎÂ‰ÒÚ‚ËÂÏ.

é Ô  Â ‰ Â Î Â Ì Ë Â. àÏÔÎËÍ‡ˆËﬂ ‰‚Ûı ‚˚ÒÍ‡Á˚ ‚‡ÌËÈ ı → Û

ÔÂ‰ÒÚ‡‚ÎﬂÂÚ ÒÓ·ÓÈ ÒÎÓÊÌÓÂ ‚˚ÒÍ‡Á˚‚‡ÌËÂ, ÎÓÊÌÓÂ ÚÓÎ¸ÍÓ ÚÓ„-

‰‡, ÍÓ„‰‡ ı ËÒÚËÌÌÓ, ‡ y ÎÓÊÌÓ.

ÄÌ‡ÎÓ„Ë˜ÌÓÂ ÓÔÂ‰ÂÎÂÌËÂ ÏÓÊÌÓ ‰‡Ú¸ Ë ‰Îﬂ ËÏÔÎËÍ‡ˆËË

= y → x.

èË ‡Ì‡ÎËÁÂ ÙÛÌÍˆËÈ Ú‡·Î. 3.6 ÏÓÊÂÚ ‚ÓÁÌËÍÌÛÚ¸ ‚ÓÔÓÒ Ó

ÚÓÏ, ÏÓÊÂÚ ÎË ·˚Ú¸ ËÒÚËÌÌ˚Ï ÒÎÓÊÌÓÂ ‚˚ÒÍ‡Á˚‚‡ÌËÂ, ÒÓÒÚ‡‚-

ÎÂÌÌÓÂ ËÁ ‰‚Ûı ÎÓÊÌ˚ı? ç‡ ˝ÚÓÚ ‚ÓÔÓÒ ËÏÂÂÚÒﬂ ÛÚ‚Â‰ËÚÂÎ¸-

Ì˚È ÓÚ‚ÂÚ: ‰‡, ÏÓÊÂÚ. ùÚÓ Ó·˙ﬂÒÌﬂÂÚÒﬂ ÚÂÏ, ˜ÚÓ ‚ ‡Î„Â·Â ÎÓ„Ë-

ÍË Î˛·ÓÂ ‚˚ÒÍ‡Á˚ ‚‡ÌËÂ ‡ÒÒÏ‡ÚË‚‡ÂÚÒﬂ ÚÓÎ¸ÍÓ Ò ÚÓ˜ÍË ÁÂ-

ÌËﬂ Â„Ó Ò‚ÓÈÒÚ‚‡ ·˚Ú¸ ÎÓÊÌ˚Ï ËÎË ËÒÚËÌÌ˚Ï, ‡ ÒÓ‰ÂÊ‡ÌËÂ

‚˚ÒÍ‡Á˚‚‡ÌËﬂ ‚ ‡Ò˜ÂÚ ÌÂ ÔËÌËÏ‡ÂÚÒﬂ. èÓ˝ÚÓÏÛ ÎÓ„Ë˜ÂÒÍËÂ

Ò‚ﬂÁË ÏÓ„ÛÚ Ó·˙Â‰ËÌﬂÚ¸ ‚˚ÒÍ‡Á˚‚‡ÌËﬂ, ÌÂ ËÏÂ˛˘ËÂ ÒÏ˚ÒÎÓ‚ÓÈ

Ò‚ﬂÁË.

îÛÌÍˆËﬂ èËÒ‡ F

(x, y) = x↓y ÔÂ‰ÒÚ‡‚ÎﬂÂÚ ÒÓ·ÓÈ ËÌ‚Â-

ÒË˛ ‰ËÁ˙˛ÌÍˆËË. ÑÎﬂ ÌÂÂ ÏÓÊÂÚ ·˚Ú¸ ‰‡ÌÓ ÒÎÂ‰Û˛˘ÂÂ ÓÔÂ-

‰ÂÎÂÌËÂ.

é Ô  Â ‰ Â Î Â Ì Ë Â. îÛÌÍˆËﬂ èËÒ‡ – ˝ÚÓ Ú‡ÍÓÂ ÒÎÓÊÌÓÂ ‚˚-

ÒÍ‡Á˚‚‡ÌËÂ, ÍÓÚÓÓÂ ËÒÚËÌÌÓ ÚÓÎ¸ÍÓ ÚÓ„‰‡, ÍÓ„‰‡ ‚ıÓ‰ﬂ˘ËÂ ‚

ÌÂ„Ó ÔÓÒÚ˚Â ‚˚ÒÍ‡Á˚‚‡ÌËﬂ ÎÓÊÌ˚.

îÛÌÍˆË˛ òÂÙÙÂ‡ F

(x, y) = ı|y ÏÓÊÌÓ ËÌÚÂÔÂÚËÓ-

‚‡Ú¸ Í‡Í ËÌ‚ÂÒË˛ ÍÓÌ˙˛ÌÍˆËË, ‡ ‚ Í‡˜ÂÒÚ‚Â ÓÔÂ‰ÂÎÂÌËﬂ ‰‡Ú¸

Ú‡ÍÓÂ.

é Ô  Â ‰ Â Î Â Ì Ë Â. îÛÌÍˆËﬂ òÂÙÙÂ‡ – ˝ÚÓ Ú‡ÍÓÂ ÒÎÓÊÌÓÂ

122

‚˚ÒÍ‡Á˚‚‡ÌËÂ, ÍÓÚÓÓÂ ÎÓÊÌÓ ÚÓÎ¸ÍÓ ‚ ÒÎÛ˜‡Â ‚ıÓ‰ﬂ˘Ëı ‚ ÌÂ„Ó

‚˚ÒÍ‡Á˚‚‡ÌËÈ Ë ËÒÚËÌÌÓ ‚ ÓÒÚ‡Î¸Ì˚ı ÒÎÛ˜‡ﬂı.

îÛÌÍˆËË èËÒ‡ Ë òÂÙÙÂ‡ ËÌÓ„‰‡ Ì‡Á˚‚‡˛Ú ÛÌË‚ÂÒ‡Î¸-

Ì˚ÏË.

ë ËÒÔÓÎ¸ÁÓ‚‡ÌËÂÏ ·‡ÁÓ‚˚ı ·ÛÎÂ‚˚ı ÙÛÌÍˆËÈ Ó‰ÌÓ„Ó Ë ‰‚Ûı

‡„ÛÏÂÌÚÓ‚, ÔËÏÂÌﬂﬂ ÏÂÚÓ‰ ÒÛÔÂ ÔÓÁËˆËÈ Ë ÔÓ‰ÒÚ‡ÌÓ‚ÍË ‡„Û-

ÏÂÌÚÓ‚, ÏÓÊÌÓ ÔÓÒÚÓËÚ¸ ·ÓÎÂÂ ÒÎÓÊÌ˚Â ÙÛÌÍˆËË ·ÓÎ¸¯Â„Ó

˜ËÒÎ‡ ÔÂÂÏÂÌÌ˚ı. ëÛÔÂÔÓÁËˆËÂÈ ‡„ÛÏÂÌÚÓ‚ Ì‡Á˚‚‡˛Ú Á‡ÏÂ-

ÌÛ ‡„ÛÏÂÌÚÓ‚ ÌÂÍÓÚÓÓÈ ÙÛÌÍˆËË ‰Û„ËÏË ÙÛÌÍˆËﬂÏË. ÇÓÁ-

ÏÓÊÌÓÒÚ¸ Ú‡ÍÓÈ ÔÓ‰ÒÚ‡ÌÓ‚ÍË ÓÔÂ‰ÂÎﬂÂÚÒﬂ ÚÂÏ, ˜ÚÓ Ó·Î‡ÒÚ¸

ÁÌ‡˜ÂÌËÈ ·ÛÎÂ‚˚ı ÙÛÌÍˆËÈ Ë Ó·Î‡ÒÚ¸ ÁÌ‡˜ÂÌËÈ Ëı ‡„ÛÏÂÌÚÓ‚

ÒÓ‚Ô‡‰‡˛Ú.

èÓ‰ÒÚ‡ÌÓ‚ÍÓÈ ‡„ÛÏÂÌÚÓ‚ Ì‡Á˚‚‡˛Ú Á‡ÏÂÌÛ ‡„ÛÏÂÌÚÓ‚ ÌÂÍÓ-

ÚÓÓÈ ÙÛÌÍˆËË ‰Û„ËÏË ‡„ÛÏÂÌÚ‡ÏË ËÎË ËÁÏÂÌÂÌËÂ ÔÓﬂ‰Í‡

Á‡ÔËÒË ‡„ÛÏÂÌÚÓ‚.

ç‡ÔËÏÂ, ‚ ÙÛÌÍˆËË F

= x

‚ÏÂÒÚÓ ‡„ÛÏÂÌÚ‡ y

ÏÓÊÌÓ

ÔÓ‰ÒÚ‡‚ËÚ¸ ÙÛÌÍˆË˛ y

= x∨x

. Ç ÂÁÛÎ¸Ú‡ÚÂ ÔÓÎÛ˜ËÏ

= x

⋅(x

∨x

ëÎÂ‰ÛÂÚ Á‡ÏÂÚËÚ¸, ˜ÚÓ ÔË ÒËÌÚÂÁÂ ÎÓ„Ë˜ÂÒÍËı ÒıÂÏ ÔËÏÂ-

Ìﬂ˛ÚÒﬂ ÚÓÎ¸ÍÓ ˝ÚË ‰‚Â Ï‡ÚÂÏ‡ÚË˜ÂÒÍËÂ ÓÔÂ‡ˆËË, Ú‡Í Í‡Í ÚÓÎ¸-

ÍÓ ÓÌË ËÏÂ˛Ú ÙËÁË˜ÂÒÍÛ˛ ËÌÚÂÔÂÚ‡ˆË˛.

èÂ‰ÒÚ‡‚ÎÂÌËÂ ·ÛÎÂ‚˚ı ÙÛÌÍˆËÈ ‚ ‚Ë‰Â ÏÌÓ„Ó˜ÎÂÌÓ‚.

èÂ‰ÒÚ‡‚ÎÂÌËÂ ·ÛÎÂ‚˚ı ÙÛÌÍˆËÈ ‚ ‚Ë‰Â ÔÓÎËÌÓÏÓ‚ ÔÓÁ‚ÓÎﬂÂÚ

ËÏÂÚ¸ ·ÓÎÂÂ Û‰Ó·ÌÛ˛ ‰Îﬂ ÔÓÒÎÂ‰Û˛˘Â„Ó ‡Ì‡ÎËÁ‡ ÙÓÏÛ ÙÛÌÍ-

ˆËË.

ê‡ÒÒÏÓÚËÏ ÔÂ‰ÒÚ‡‚ÎÂÌËÂ ·ÛÎÂ‚˚ı ÙÛÌÍˆËÈ ‚ ‚Ë‰Â Ú‡Í Ì‡-

Á˚‚‡ÂÏ˚ı ÌÓÏ‡Î¸Ì˚ı ÙÓÏ.

é Ô  Â ‰ Â Î Â Ì Ë Â. ÑËÁ˙˛ÌÍÚË‚ÌÓÈ ÌÓÏ‡Î¸ÌÓÈ ÙÓÏÓÈ

(Ñçî) ·ÛÎÂ‚ÓÈ ÙÛÌÍˆËË n-‡„ÛÏÂÌÚÓ‚ Ì‡Á˚‚‡˛Ú ‰ËÁ˙˛ÌÍˆË˛

Î˛·˚ı ˝ÎÂÏÂÌÚ‡Ì˚ı ÍÓÌ˙˛ÌÍˆËÈ ˝ÚËı ‡„ÛÏÂÌÚÓ‚.

ç‡ÔËÏÂ,

Fxxx xx xx xx

(

)

1 23 1 2231 3

= ⋅∨⋅∨⋅ Ô Â‰ÒÚ‡‚-

ÎﬂÂÚ ÒÓ·ÓÈ Ñçî, ‡ ˜ÎÂÌ˚, ‚ıÓ‰ﬂ˘ËÂ ‚ ÌÂÂ

xxxx

1 223

⋅⋅,,

1 3

⋅ – ˝ÎÂÏÂÌÚ‡Ì˚ Â ÍÓÌ˙˛ÌÍˆËË. ùÎÂÏÂÌÚ‡Ì˚Â ÍÓÌ˙˛ÌÍ-

ˆËË ÏÓ„ÛÚ ÒÓ‰ÂÊ‡Ú¸ Î˛·ÓÂ ÍÓÎË˜ÂÒÚ‚Ó ‡„ÛÏÂÌÚÓ‚ ÙÛÌÍˆËË.

äÓÏÂ ‰ËÁ˙˛ÌÍÚË‚ÌÓÈ ÌÓÏ‡Î¸ÌÓÈ ÙÓÏ˚ ÏÓÊÂÚ ·˚Ú¸ ÓÔÂ‰Â-

ÎÂÌ‡ Ë ÍÓÌ˙˛ÌÍÚË‚Ì‡ﬂ ÌÓÏ‡Î¸Ì‡ﬂ ÙÓ Ï‡.

é Ô  Â ‰ Â Î Â Ì Ë Â. äÓÌ˙˛ÌÍÚË‚ÌÓÈ ÌÓÏ‡Î¸ÌÓÈ ÙÓÏÓÈ

(äçî) ÙÛÌÍˆËË n-‡„ÛÏÂÌÚÓ‚ Ì‡Á˚‚‡˛ Ú ÍÓÌ˙˛ÌÍˆË˛ ˝ÎÂÏÂÌ-

Ú‡Ì˚ı ‰ËÁ˙˛ÌÍˆËÈ ˝ÚËı ‡„ÛÏÂÌÚÓ‚.

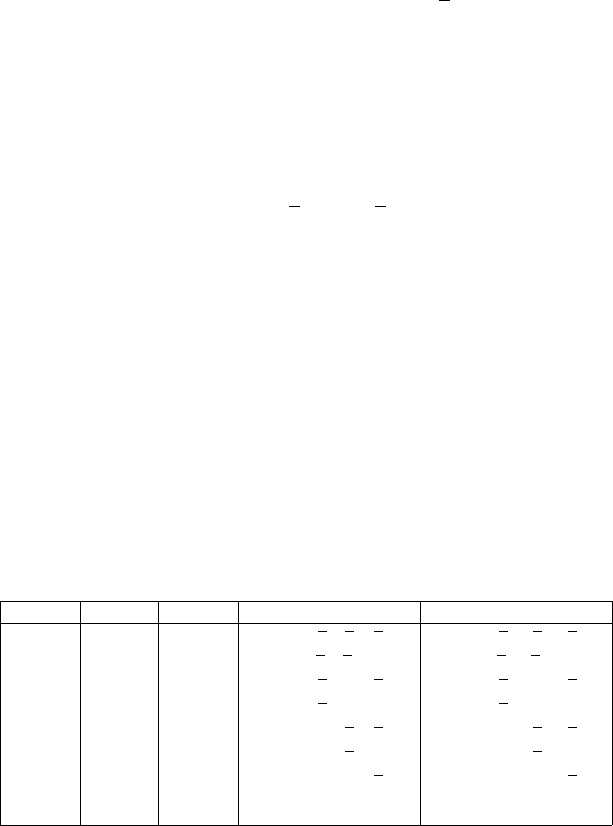
ç‡ÔËÏÂ,

Fx x x x x x x(, , ) ( )( )

1 23 1 22 3

= ∨∨ ﬂ‚Îﬂ ÂÚÒﬂ äçî,

‡ ˜ÎÂÌ˚

(),()xx xx

1 223

∨∨ Ì‡Á˚‚‡˛ÚÒﬂ ˝ ÎÂÏÂÌÚ‡Ì˚ ÏË ‰ËÁ˙-

˛ÌÍˆËﬂÏË.

123

ùÎÂÏÂÌÚ‡Ì˚Â ÍÓÌ˙˛ÌÍˆËË, ‚ ÍÓÚÓ˚Â ‚ıÓ‰ﬂÚ ‚ÒÂ ‡„ÛÏÂÌÚ˚

ÙÛÌÍˆËË ‚ ÔﬂÏÓÈ ËÎË ËÌ‚ÂÒÌÓÈ ÙÓÏÂ, Ì‡Á˚‚‡˛Ú ÍÓÌÒÚË-

ÚÛÂÌÚ‡ÏË Â‰ËÌËˆ˚ ËÎË ÏËÌÚÂÏ‡ÏË.

é Ô  Â ‰ Â Î Â Ì Ë Â. äÓÌÒÚËÚÛÂÌÚÓÈ Â‰ËÌËˆ˚ (ÏËÌÚÂÏÓÏ)

Ì‡Á˚‚‡˛Ú Ú‡ÍÛ˛ ·ÛÎÂ‚Û ÙÛÌÍˆË˛ n-‡„ÛÏÂÌÚÓ‚, ÍÓÚÓ‡ﬂ ‡‚Ì‡

Â‰ËÌËˆÂ ÚÓÎ¸ÍÓ Ì‡ Ó‰ÌÓÏ Ì‡·ÓÂ ˝ÚËı ‡„ÛÏÂÌÚÓ‚.

ç‡ÔËÏÂ, ÙÛÌÍˆËﬂ F(x

, x

) = x

⋅

⋅x

, ﬂ‚Îﬂ˛˘‡ﬂÒﬂ

ÍÓÌÒÚËÚÛÂÌÚÓÈ Â‰ËÌËˆ˚, ‡‚Ì‡ Â‰ËÌËˆÂ ÚÓÎ¸ÍÓ Ì‡ Ì‡·ÓÂ (1, 0,

1), Ì‡ ÓÒÚ‡Î¸Ì˚ı Ì‡·Ó‡ı ÓÌ‡ ‡‚Ì‡ ÌÛÎ˛.

ÄÌ‡ÎÓ„Ë˜ÌÓ ˝ÎÂÏÂÌÚ‡Ì˚Â ‰ËÁ˙˛ÌÍˆËË, ‚ ÍÓÚÓ˚Â ‚ıÓ‰ﬂÚ

‚ÒÂ ‡„ÛÏÂÌÚ˚ ÙÛÌÍˆËË ‚ ÔﬂÏÓÈ ËÎË ËÌ‚ÂÒÌÓÈ ÙÓÏÂ, ÌÓÒﬂÚ

Ì‡Á‚‡ÌËÂ ÍÓÌÒÚËÚÛÂÌÚ ÌÛÎﬂ ËÎË Ï‡ÍÒÚÂÏÓ‚.

é Ô  Â ‰ Â Î Â Ì Ë Â. äÓÌÒÚËÚÛÂÌÚÓÈ ÌÛÎﬂ (Ï‡ÍÒÚÂÏÓÏ) Ì‡-

Á˚‚‡˛Ú Ú‡ÍÛ˛ ·ÛÎÂ‚Û ÙÛÌÍˆË˛ n-‡„ÛÏÂÌÚÓ‚, ÍÓÚÓ‡ﬂ ‡‚Ì‡

ÌÛÎ˛ ÚÓÎ¸ÍÓ Ì‡ Ó‰ÌÓÏ Ì‡·ÓÂ ˝ÚËı ‡„ÛÏÂÌÚÓ‚.

ç‡ÔËÏÂ, F(x

, x

) =

xxx

1 23

∨∨ ‡‚Ì‡ ÌÛÎ˛ ÚÓÎ¸ÍÓ Ì‡

Ì‡·ÓÂ (1, 0, 1) Ë  ‡‚Ì‡ Â‰ËÌËˆÂ Ì‡ ÓÒÚ‡Î¸Ì˚ı Ì‡·Ó‡ı.

ó‡ÒÚÓ Ó·ÓÁÌ‡˜‡˛Ú ÍÓÌÒÚËÚÛÂÌÚÛ Â‰ËÌËˆ˚ ·ÛÍ‚ÓÈ m

, ‡ ÍÓÌ-

ÒÚËÚÛÂÌÚÛ ÌÛÎﬂ ·ÛÍ‚ÓÈ M

. ÑÎﬂ ÔÓÎÛ˜ÂÌËﬂ ËÌ‰ÂÍÒ‡ ÔÓ‰ ÔÂÂ-

ÏÂÌÌ˚ÏË, ‚ıÓ‰ﬂ˘ËÏË ‚ ÍÓÌÒÚËÚÛÂÌÚÛ ‚ ÔﬂÏÓÈ ÙÓÏÂ, Á‡ÔËÒ˚-

‚‡˛Ú Â‰ËÌËˆÛ, ‡ ÔÓ‰ ÔÂÂÏÂÌÌ˚ÏË ‚ ËÌ‚ÂÒÌÓÈ ÙÓÏÂ – ÌÛÎ¸.

èÓÎÛ˜ÂÌÌÓÈ ÒÓ‚ÓÍÛÔÌÓÒÚË ÌÛÎÂÈ Ë Â‰ËÌËˆ ÒÚ‡‚ﬂÚ ‚ ÒÓÓÚ‚ÂÚ-

ÒÚ‚ËÂ ‰‚ÓË˜ÌÓÂ ˜ËÒÎÓ, ‰ÂÒﬂÚË˜Ì˚È ˝Í‚Ë‚‡ÎÂÌÚ ÍÓÚÓÓ„Ó Ë ﬂ‚Îﬂ-

ÂÚÒﬂ ËÌ‰ÂÍÒÓÏ.

Ç Í‡˜ÂÒÚ‚Â ÔËÏÂ‡ ‚ Ú‡·Î. 3.7 ÔË‚Â‰ÂÌ˚ ‚ÒÂ ÍÓÌÒÚËÚÛÂÌÚ˚

ÌÛÎﬂ Ë Â‰ËÌËˆ˚ ÙÛÌÍˆËË ÚÂı ‡„ÛÏÂÌÚÓ‚.

ó‡ÒÚÓ ‰Îﬂ ÒÓÍ‡˘ ÂÌËﬂ Á‡ÔËÒË ÒËÏ‚ÓÎ˚ m Ë å ÓÔÛÒÍ‡˛ÚÒﬂ Ë

Á‡ÔËÒ˚‚‡˛ÚÒﬂ ÚÓÎ¸ÍÓ ‰ÂÒﬂÚË˜Ì˚Â ÌÓÏÂ‡ ÍÓÌÒÚËÚÛÂÌÚ.

ç‡ÔËÏÂ, ‚ÏÂÒÚÓ

í‡·ÎËˆ‡ 3.7

äÓÌÒÚËÚÛÂÌÚ˚ ÙÛÌÍˆËË ÚÂı ÔÂÂÏÂÌÌ˚ı

000

mxxx

0 1 23

= ⋅⋅

Mxxx

0 1 23

= ∨∨

001

mxxx

1123

= ⋅⋅

Mxxx

1123

= ∨∨

0 1 0

mxxx

2 1 23

= ⋅⋅

Mxxx

2 1 23

= ∨∨

0 11

mxxx

3 1 23

= ⋅⋅

Mxxx

3 1 23

= ∨∨

1 00

mxxx

4 1 23

= ⋅⋅

Mxxx

4 1 23

= ∨∨

1 0 1

mxxx

5 1 23

= ⋅⋅

Mxxx

5 1 23

= ∨∨

110

mxxx

6 1 23

= ⋅⋅

Mxxx

6 1 23

= ∨∨

111

mxxx

7 1 23

= ⋅⋅

Mxxx

7 1 23

= ∨∨

124

F(x

, x

) = m

∨m

ÏÓÊÌÓ Á‡ÔËÒ‡Ú¸

F(x

, x

) = ∨(1, 2, 3),

‡ ‚ÏÂÒÚÓ

F(x

, x

) = M

⋅M

Á‡ÔËÒ˚‚‡˛Ú

F(x

, x

) = &(0, 3, 5, 6).

ë‚ÓÈÒÚ‚‡ ÍÓÌÒÚËÚÛÂÌÚ

−

2 1

1. (3.7)

ÑËÁ˙˛ÌÍˆËﬂ ‚ÒÂı ÍÓÌÒÚËÚÛÂÌÚ Â‰ËÌËˆ˚ ÙÛÌÍˆËË

n-‡„ÛÏÂÌÚÓ‚  ‡‚Ì‡ Â‰ËÌËˆÂ. èÓÍ‡ÊÂÏ ˝ÚÓ ÔË n = 2:

mmmmm

= ∨∨∨

0 1 23

, ËÎË

mxxxxxxxx

= ⋅∨⋅∨⋅∨⋅=

1 2 1 2 1 2 1 2

= ∨∨⋅∨= ∨ =xx x x x x x x

1 22 1 22 11

1()() .

−

2 1

0. (3.8)

äÓÌ˙˛ÌÍˆËﬂ ‚ÒÂı ÍÓÌÒÚËÚÛÂÌÚ ÌÛÎﬂ ÙÛÌÍˆËË n-‡„ÛÏÂÌÚÓ‚

‡‚Ì‡ ÌÛÎ˛. èÓÍ‡ÊÂÏ ˝ÚÓ ÔË n = 2:

MMMMM

= ⋅⋅⋅

0 1 23

, ËÎË

Mxxxxxxxx

= ∨⋅∨⋅∨⋅∨ =

1 2 1 2 1 2 1 2

()()()()

= ∨⋅∨⋅ ∨ ⋅∨⋅ = ⋅ =()().x xx xx x xx xx xx

112 1 2 112 1 2 11

åÌÓ„ËÂ ÔÂÓ·‡ÁÓ‚‡ÌËﬂ, ‚˚ÔÓÎÌﬂÂÏ˚Â Ì‡‰ ·ÛÎÂ‚˚ÏË ÙÛÌÍ-

ˆËﬂÏË, Û‰Ó·ÌÓ ËÌÚÂÔÂÚËÛ˛ÚÒﬂ Ò ÔÓÏÓ˘¸˛ „ÂÓÏÂÚË˜ÂÒÍËı

ÔÂ‰ÒÚ‡‚ÎÂÌËÈ ·ÛÎÂ‚˚ı ÙÛÌÍˆËÈ.

ä‡Ê‰˚È Ì‡·Ó ·ÛÎÂ‚˚ı ÔÂÂÏÂÌÌ˚ı (ı

, ı

,..., x

) ÏÓÊÂÚ

‡ÒÒÏ‡Ú Ë‚‡Ú¸Òﬂ Í‡Í n-ÏÂÌ˚È ‚ÂÍÚÓ, ÓÔÂ‰ÂÎﬂ˛˘ËÈ ÚÓ˜ÍÛ

125

n-ÏÂÌÓ„Ó ÔÓÒÚ‡ÌÒÚ‚‡. ëÎÂ‰Ó‚‡ÚÂÎ¸ÌÓ, ‚ÒÂ ÏÌÓÊÂÒÚ‚Ó Ì‡·Ó-

Ó‚, Ì‡ ÍÓÚÓ˚ı ÓÔ Â‰ÂÎÂÌ‡ ÙÛÌÍˆËﬂ n-ÔÂÂÏÂÌÌ˚ı, ÏÓÊÌÓ

ÔÂ‰ÒÚ‡‚ËÚ¸ ‚ ‚Ë‰Â ‚Â¯ËÌ n-ÏÂÌÓ„Ó ÍÛ·‡.

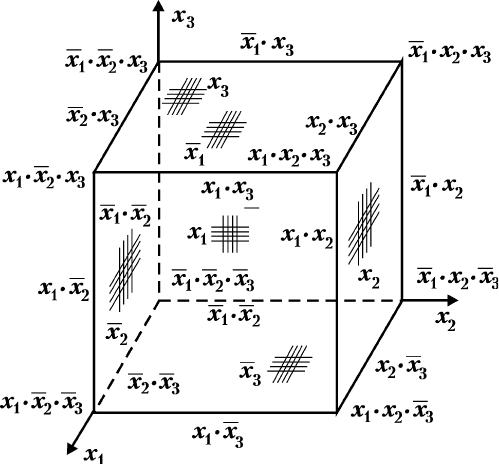
ÇÂ¯ËÌ‡Ï ÍÛ·‡ ÒÓÔÓÒÚ‡‚Îﬂ˛ÚÒﬂ ÍÓÌÒÚËÚÛÂÌÚ˚ Â‰ËÌËˆ˚. ÉÂ-

ÓÏÂÚË˜ÂÒÍ‡ﬂ ËÌÚÂÔÂÚ‡ˆËﬂ Ó·Î‡ÒÚË ÓÔÂ‰ÂÎÂÌËﬂ ÙÛÌÍˆËË

ÚÂı ÔÂÂÏÂÌÌ˚ı ÔÂ‰ÒÚ‡‚ÎÂÌ‡ Ì‡ ËÒ. 3.6.

Ñ‚Â ‚Â¯ËÌ˚ Ì‡Á˚‚‡˛ÚÒﬂ ÒÓÒÂ‰ÌËÏË, ÂÒÎË ÓÌË ÓÚÎË˜‡˛ÚÒﬂ

‰Û„ ÓÚ ‰Û„‡ ÚÓÎ¸ÍÓ Ó‰ÌÓÈ ÔÂÂÏÂÌÌÓÈ, ÒÎÂ‰Ó‚‡ÚÂÎ¸ÌÓ, Â· ‡Ï,

ÒÓÂ‰ËÌﬂ˛˘ËÏ ‰‚Â ÒÓÒÂ‰ÌËÂ ‚Â¯ËÌ˚, ÒÓÓÚ‚ÂÚÒÚ‚Û˛Ú ˝ÎÂÏÂÌ-

Ú‡Ì˚ Â ÍÓÌ˙˛ÌÍˆËË ‡Ì„‡ (n – 1).

é Ô  Â ‰ Â Î Â Ì Ë Â. ê‡Ì„ÓÏ ÍÓÌ˙˛ÌÍˆËË Ì‡Á˚‚‡˛Ú ÍÓÎË˜ÂÒÚ‚Ó

ÔÂÂÏÂÌÌ˚ı, ‚ıÓ‰ﬂ˘Ëı ‚ ÌÂÂ.

îÛÌÍˆËË ÚÂı ÔÂÂÏÂÌÌ˚ı ÒÓÓÚ‚ÂÚÒÚ‚ÛÂÚ ÍÓÌ˙˛ÌÍˆËﬂ ‚ÚÓ-

Ó„Ó ‡Ì„‡.

äÓÌ˙˛ÌÍˆËË ÔÂ‚Ó„Ó ‡Ì„‡ ÒÓÓÚ‚ÂÚÒÚ‚Û˛Ú „‡ÌﬂÏ ÍÛ·‡.

ä‡Ê‰‡ﬂ ‚Â¯ËÌ‡ ÍÛ·‡ ÓÔÂ‰ÂÎﬂÂÚÒﬂ Ì‡·ÓÓÏ ‡„ÛÏÂÌÚÓ‚ (ı

,..., x

). Ç ÒÎÛ˜‡Â „ÂÓÏÂÚË˜ÂÒÍÓ„Ó ÔÂ‰ÒÚ‡‚ÎÂÌËﬂ Ì‡·Ó (ı

,..., x

) ÔËÌﬂÚÓ Ì‡Á˚‚‡Ú¸ 0-ÍÛ·ÓÏ. åÌÓÊÂÒÚ‚Ó 0-ÍÛ·Ó‚, Ì‡

ÍÓÚÓ˚ı ÙÛÌÍˆËﬂ ÔËÌËÏ‡ÂÚ Â‰ËÌË˜Ì˚Â ÁÌ‡˜ÂÌËﬂ, Ì‡Á˚‚‡˛Ú

ÍÛ·Ë˜ÂÒÍËÏ ÍÓÏÔÎÂÍÒÓÏ K

êàë. 3.6

126

ç‡ÔËÏÂ, ÂÒÎË Á‡‰‡Ì‡ ÙÛÌÍˆËﬂ F(x

, x

) = V(3, 4, 5, 6,

7), ÚÓ ÍÛ·Ë˜ÂÒÍËÈ ÍÓÏÔÎÂÍÒ K

ËÏÂÂÚ ‚Ë‰

011

100

10 1

11 0

111





















Ë ÒÓÒÚÓËÚ ËÁ ÔﬂÚË 0-ÍÛ·Ó‚, ÒÓÓÚ‚ÂÚÒÚ‚Û˛˘Ëı ÔﬂÚË Ì‡·Ó‡Ï ‡-

„ÛÏÂÌÚÓ‚ (ı

, ı

ÖÒÎË ‰‚‡ 0-ÍÛ·‡ ‡ÁÎË˜‡˛ÚÒﬂ ÚÓÎ¸ÍÓ Ó‰ÌÓÈ ÔÂÂÏÂÌÌÓÈ, ÚÓ

‰‚‡ 0-ÍÛ·‡ Ó·‡ÁÛ˛Ú 1-ÍÛ·, ÓÌ ÒÓÓÚ‚ÂÚÒÚ‚ÛÂÚ Ó·˘ËÏ ˝ÎÂÏÂÌÚ‡Ï

0-ÍÛ·Ó‚, ÔË˜ÂÏ ‚ÏÂÒÚÓ ÍÓÓ‰ËÌ‡Ú˚, ÍÓÚÓÓÈ ‡ÁÎË˜‡˛ÚÒﬂ

0-ÍÛ·˚, Á‡ÔËÒ˚‚‡ÂÚÒﬂ

ï,

Ó·ÓÁÌ‡˜‡˛˘ËÈ

ÌÂÁ‡‚ËÒËÏÛ˛

ÍÓÓ‰ËÌ‡ÚÛ.

äÛ·Ë˜ÂÒÍËÈ ÍÓÏÔÎÂÍÒ K

, ÒÓ‰ÂÊ‡˘ËÈ ‚ÒÂ ÏÌÓÊÂÒÚ‚Ó

1-ÍÛ·Ó‚ ‰Îﬂ ‰‡ÌÌÓ„Ó ÔËÏÂ‡:

1 0





















äÓÏÔÎÂÍÒ K

Ú‡ÍÊÂ ÒÓÒÚÓËÚ ËÁ ÔﬂÚË 1-ÍÛ·Ó‚.

ÄÌ‡ÎÓ„Ë˜ÌÓ ËÁ ÍÓÏÔÎÂÍÒ‡ K

ÏÓÊÌÓ ÔÓÎÛ˜ËÚ¸ ÍÛ·Ë˜ÂÒÍËÈ

ÍÓÏÔÎÂÍÒ K

; ÓÌ ÒÓ‰ÂÊËÚ Ó‰ËÌ 2-ÍÛ·:

KXX

{}

1 .

Ç ˝ÚÓÏ ÔËÏÂÂ 3-ÍÛ·˚ ÓÚÒÛÚÒÚ‚Û˛Ú, ËÌ‡˜Â „Ó‚Óﬂ, ÍÓÏÔÎÂÍÒ

ÔÂ‰ÒÚ‡‚ÎﬂÂÚÒﬂ ÔÛÒÚ˚Ï ÏÌÓÊÂÒÚ‚ÓÏ K

= 0. à ‰‡ÎÂÂ ÏÓÊÌÓ ÔÓ-

Í‡Á‡Ú¸, ÔÓ ËÌ‰ÛÍˆËË, ˜ÚÓ ‰‚‡ r-ÍÛ·‡, ÒÓ‰ÂÊ‡˘ËÂ r Ó‰ÌÓËÏÂÌ-

Ì˚ı ÌÂÁ‡‚ËÒËÏ˚ı ÍÓÓ‰ËÌ‡Ú Ë  ‡ÁÎË˜‡˛˘ËÂÒﬂ ÚÓÎ¸ÍÓ Ó‰ÌÓÈ

ÍÓÓ‰ËÌ‡ÚÓÈ, ÏÓ„ÛÚ Ó·‡ÁÓ‚˚‚‡Ú¸ (r + 1)-ÍÛ·, „‰Â (r + 1) ÌÂÁ‡-

‚ËÒËÏ‡ﬂ ÍÓÓ‰ËÌ‡Ú‡ ÒÓÓÚ‚ÂÚÒÚ‚ÛÂÚ ÚÓÈ ÍÓÓ‰ËÌ‡ÚÂ, ÔÓ ÍÓÚÓÓÈ

‡ÁÎË˜‡˛ÚÒﬂ r-ÍÛ·˚. óËÒÎÓ ÌÂÁ‡‚ËÒËÏ˚ı ÍÓÓ‰ËÌ‡Ú ï ‚ r-ÍÛ·Â

ÓÔÂ‰ÂÎﬂÂÚ Â„Ó ‡ÁÏÂÌÓÒÚ¸, Ì‡ÔËÏÂ, ÍÛ· 01ï0ï1ï ËÏÂÂÚ

‡ÁÏÂÌÓÒÚ¸ r = 3.

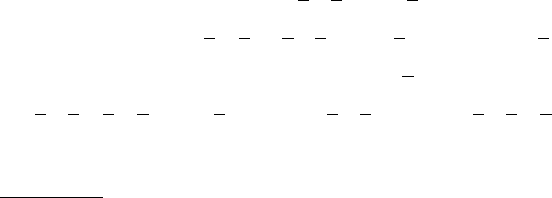
é·˙Â‰ËÌÂÌËÂ ÍÛ·Ë˜ÂÒÍËı ÍÓÏÔÎÂÍÒÓ‚ K

, K

,..., K

ÙÛÌÍˆËË

F(x

, x

,..., x

) Ì‡Á˚‚‡˛Ú ÍÛ·Ë˜ÂÒÍËÏ ÍÓÏÔÎÂÍÒÓÏ K(F) ÙÛÌÍ-

ˆËË F. ÑÎﬂ ‰‡ÌÌÓ„Ó ÔËÏÂ‡

127

KF K K K

() .= ∨∨ =





















0 1 2

011

100

10 1

111

1 0

èÓ Ò‡‚ÌÂÌË˛ Ò ‡Ì‡ÎËÚË˜ÂÒÍËÏË ÙÓÏ‡ÏË Á‡ÔËÒË ·ÛÎÂ-

‚˚ı ÙÛÌÍˆËÈ, „ÂÓÏÂÚ Ë˜ÂÒÍËÂ ÙÓÏ˚ ÌÂÒÍÓÎ¸ÍÓ ·ÓÎÂÂ ÍÓÏ-

Ô‡ÍÚÌ˚ Ë ËÒÔÓÎ¸ÁÛ˛Ú ÏÂÌ¸¯ÂÂ ÍÓÎË˜ÂÒÚ‚Ó ÒËÏ‚ÓÎÓ‚. äÓÏÂ

ÚÓ„Ó, „ÂÓÏÂÚË˜ÂÒÍÓÂ ÔÂ‰ÒÚ‡‚ÎÂÌËÂ ·ÛÎÂ‚˚ı ÙÛÌÍˆËÈ ÔÓÁ‚ÓÎﬂ-

ÂÚ ‰Îﬂ Ëı ‡Ì‡ÎËÁ‡ ËÒÔÓÎ¸ÁÓ‚‡Ú¸ ‡Î„Â·Ó-ÚÓÔÓÎÓ„Ë˜ÂÒÍËÂ ÏÂÚÓ-

‰˚, ÍÓÚÓ˚Â ‚ ﬂ‰Â ÒÎÛ˜‡Â‚ ·ÓÎÂÂ ˝ ÙÙÂÍÚË‚Ì˚, ˜ÂÏ ‡Ì‡ÎËÚË˜Â-

ÒÍËÂ.

ÑÛ„ÓÈ ÙÓÏÓÈ „ÂÓÏÂÚË˜ÂÒÍÓ„Ó ÔÂ‰ÒÚ‡‚ÎÂÌËﬂ ·ÛÎÂ‚˚ı

ÙÛÌÍˆËÈ ﬂ‚Îﬂ˛ÚÒﬂ Í‡Ú˚ ÇÂÈ˜‡

∗

, ÍÓÚÓ˚Â ÔÂ‰ÒÚ‡‚Îﬂ˛Ú ÒÓ·ÓÈ

‡Á‚ÂÚÍÛ ÍÛ·Ó‚ Ì‡ ÔÎÓÒÍÓÒÚË, ÔË˜ÂÏ ‚Â¯ËÌ˚ ÍÛ·Ó‚ Ì‡

Í‡Ú‡ı ÇÂÈ˜‡ ÔÂ‰ÒÚ‡‚Îﬂ˛ÚÒﬂ ÍÎÂÚÍ‡ÏË, ÍÓÓ‰ËÌ‡Ú˚ ÍÓÚÓ-

˚ı ÒÓ‚Ô‡‰‡˛Ú Ò ÍÓÓ‰ËÌ‡Ú‡ÏË ÒÓÓÚ‚ÂÚÒÚ‚Û˛˘Ëı ‚Â¯ËÌ ÍÛ-

·Ó‚.

Ç ÍÎÂÚÍ‡ı Í‡Ú˚ ÇÂÈ˜‡ ÒÚ‡‚ËÚÒﬂ ÓÚÏÂÚÍ‡ (Ó·˚˜ÌÓ Â‰Ë-

ÌËˆ‡).

ç‡ÔËÏÂ, ‡ÒÒÏÓÚËÏ ËÒÔÓÎ¸ÁÓ‚‡ÌËÂ Í‡Ú ÇÂÈ˜‡ ‰Îﬂ ËÁÓ·-

‡ÊÂÌËﬂ ÙÛÌÍˆËÈ:

Fx x x x x x

11 2 1 2 1 2

(, ) ;= ⋅∨⋅

Fxxx xxx xxx xxx xxx

2 1 23 1 23 1 23 1 23 1 23

(, , ) ;= ⋅⋅∨⋅⋅∨⋅⋅∨⋅⋅

Fxxxx xxxx xxxx

3 1 234 1 234 1 234

(,,,)= ⋅⋅⋅∨⋅⋅⋅∨

∨⋅⋅⋅∨⋅⋅⋅∨⋅⋅⋅∨⋅⋅⋅xxxx xxxx xxxx xxxx

1 234 1 234 1 234 1 234

ùÚËÏ ÙÛÌÍˆËﬂÏ ÒÓÓÚ‚ÂÚÒÚ‚Û˛Ú ÍÛ·Ë˜ÂÒÍËÂ ÍÓÏÔÎÂÍÒ˚:

∗

àÒÔÓÎ¸ÁÓ‚‡ÌËÂ

ÔÎÓÒÍÓÒÚÌÓ„Ó

ËÁÓ·‡ÊÂÌËﬂ

ÍÛ·Ë˜ÂÒÍËı

ÍÓÏÔÎÂÍÒÓ‚

‰Îﬂ ‡Ì‡-

ÎËÁ‡ ·ÛÎÂ‚˚ı ÙÛÌÍˆËÈ ·˚ÎÓ ÔÂ‰ÎÓÊÂÌÓ ‡ÏÂËÍ‡ÌÒÍËÏ Û˜ÂÌ˚Ï Ö.á. ÇÂÈ˜ÂÏ ‚

1952 „.