Овчаров Л.А. и др. Математические модели информационых процессов и управления

Подождите немного. Документ загружается.

ìÑä 681.518+001.891.573

ÅÅä 32.97

å 33

ê Â ˆ Â Ì Á Â Ì Ú ‡Í‡‰ÂÏËÍ êÄç ‰ÓÍÚÓ ÚÂıÌË˜ÂÒÍËı Ì‡ÛÍ,

ÔÓÙÂÒÒÓ ç.Ä. äÛÁÌÂˆÓ‚

Ä‚ÚÓ˚:

ã.Ä. éÇóÄêéÇ, Ç.ë. ÅàíûäéÇ, Ç.å. ÇéãäéÇ, é.Ç. ûÑéÇëäàâ,

É.è. åéãéíäéÇ

, Å.ã. äìóàç, à.ë. äìêéèíÖÇÄ

äÌË„‡ ‚˚ÔÛ˘ÂÌ‡ ÔË ÒÓ‰ÂÈÒÚ‚ËË éÄé “É‡ÁÔÓÏ”

å‡ÚÂÏ‡ÚË˜ÂÒÍËÂ ÏÓ‰ÂÎË ËÌÙÓÏ‡ˆËÓÌÌ˚ı ÔÓˆÂÒÒÓ‚

å 33 Ë ÛÔ‡‚ÎÂÌËﬂ: ì˜Â·. ‰Îﬂ ‚ÛÁÓ‚. – å.: éÄé “àÁ‰‡-

ÚÂÎ¸ÒÚ‚Ó “çÂ‰‡”, 2001. – 247 Ò.: ËÎ.

ISBN 5-247-03873-8

ê‡ÒÒÏÓÚÂÌ˚ Ï‡ÚÂÏ‡ÚË˜ÂÒÍËÂ ÏÂÚÓ‰˚, ËÒÔÓÎ¸ÁÛÂÏ˚Â ‰Îﬂ ÔÓÒÚÓÂ-

ÌËﬂ Ï‡ÚÂÏ‡ÚË˜ÂÒÍËı ÏÓ‰ÂÎÂÈ ËÌÙÓÏ‡ˆËÓÌÌ˚ı ÔÓˆÂÒÒÓ‚ Ë ÛÔ‡‚ÎÂ-

ÌËﬂ: ÚÂÓËﬂ ÏÌÓÊÂÒÚ‚, ÚÂÓËﬂ „‡ÙÓ‚, Ï‡ÚÂÏ‡ÚË˜ÂÒÍ‡ﬂ ÎÓ„ËÍ‡ Ë ÚÂÓ Ëﬂ

ÌÂ˜ÂÚÍËı ÏÌÓÊÂÒÚ‚. èË‚Â‰ÂÌÓ ÏÌÓ„Ó ÔËÏÂÓ‚ ÔÓÒÚÓÂÌËﬂ ˝ÎÂÏÂÌÚÓ‚

Ï‡ÚÂÏ‡ÚË˜ÂÒÍËı ÏÓ‰ÂÎÂÈ ËÌÙÓÏ‡ˆËÓÌÌ˚ı ÔÓˆÂÒÒÓ‚ Ë ÛÔ‡‚ÎÂÌËﬂ.

ÑÎﬂ ÒÚÛ‰ÂÌÚÓ‚ ÚÂıÌË˜ÂÒÍËı ‚ÛÁÓ‚, Ó·Û˜‡˛˘ËıÒﬂ ÔÓ ÒÔÂˆË‡Î¸ÌÓÒÚË

“Ä‚ÚÓÏ‡ÚËÁËÓ‚‡ÌÌ˚Â ÒËÒÚÂÏ˚ Ó·‡·ÓÚÍË ËÌÙÓÏ‡ˆËË Ë ÛÔ‡‚ÎÂÌËﬂ”.

ISBN 5-247-03873-8  äÓÎÎÂÍÚË‚ ‡‚ÚÓÓ‚, 2001

 éÙÓÏÎÂÌËÂ. éÄé

“àÁ‰‡ÚÂÎ¸ÒÚ‚Ó “çÂ‰‡”, 2001

1.1. éëçéÇçõÖ èéçüíàü íÖéêàà åçéÜÖëíÇ,

éèÖêÄñàà çÄÑ åçéÜÖëíÇÄåà

ä‡Í ÛÊÂ ÛÔÓÏËÌ‡ÎÓÒ¸ ‚Ó ‚‚Â‰ÂÌËË, ÒÂ‰Ë Ï‡ÚÂÏ‡ÚË˜ÂÒÍËı

ÏÂÚÓ‰Ó‚, Ò ÔÓÏÓ˘¸˛ ÍÓÚÓ˚ı ÒÓÒÚ‡‚Îﬂ˛ÚÒﬂ Ï‡ÚÂÏ‡ÚË˜ÂÒÍËÂ ÏÓ-

‰ÂÎË ËÌÙÓÏ‡ˆËÓÌÌ˚ı ÔÓˆÂÒÒÓ‚ Ë ÛÔ‡‚ÎÂÌËﬂ, ËÒÔÓÎ¸ÁÛ˛ÚÒﬂ

ÏÂÚÓ‰˚ ÚÂÓËË ÏÌÓÊÂÒÚ‚. íÂÓËﬂ ÏÌÓÊÂÒÚ‚ ÌÛÊÌ‡ ÔÂÊ‰Â ‚ÒÂ-

„Ó ‰Îﬂ Ó·ÓÒÌÓ‚‡ÌËﬂ ÒÓ‚ÂÏÂÌÌÓÈ ÚÂÓËË ÒÎÛ˜‡ÈÌ˚ı ﬂ‚ÎÂÌËÈ.

äÓÏÂ ÚÓ„Ó, ÚÂÓËﬂ ÏÌÓÊÂÒÚ‚ Ì‡ﬂ‰Û Ò ÚÂÓËÂÈ „‡ÙÓ‚ ¯ËÓÍÓ

ËÒÔÓÎ¸ÁÛÂÚÒﬂ ÔË ÔÓÒÚÓÂÌËË ÏÓ‰ÂÎÂÈ ‡‚ÚÓÏ‡ÚËÁËÓ‚‡ÌÌ˚ı

·‡ÌÍÓ‚ ‰‡ÌÌ˚ı Ë ·‡ÌÍÓ‚ ÁÌ‡ÌËÈ: ·‡Á ‰‡ÌÌ˚ı, ËÌÙÓÏ‡ˆËÓÌÌ˚ı

ﬂÁ˚ÍÓ‚ Ë Ú.Ô. ÇÓÓ·˘Â ÚÛ‰ÌÓ ÒÍ‡Á‡Ú¸, ‚ Í‡ÍËı ‰ËÒˆËÔÎËÌ‡ı

ÒÔÂˆË‡Î¸ÌÓÒÚË “Ä‚ÚÓÏ‡ÚËÁËÓ‚‡ÌÌ˚Â ÒËÒÚÂÏ˚ Ó·‡·ÓÚÍË ËÌ-

ÙÓÏ‡ˆËË Ë ÛÔ‡‚ÎÂÌËﬂ” ÌÂ ËÒÔÓÎ¸ÁÛ˛ÚÒﬂ ÚÂ ËÎË ËÌ˚Â ÔÓÌﬂ-

ÚËﬂ Ë ÔÓÎÓÊÂÌËﬂ ÚÂÓËË ÏÌÓÊÂÒÚ‚.

åÌÓÊÂÒÚ‚ÓÏ Ì‡Á˚‚‡ÂÚÒﬂ Î˛·‡ﬂ ÒÓ‚ÓÍÛÔÌÓÒÚ¸ Ó·˙ÂÍÚÓ‚

(ﬂ‚ÎÂÌËÈ, ÔÂ‰ÏÂÚÓ‚) ÔÓËÁ‚ÓÎ¸ÌÓÈ ÔËÓ‰˚, Í‡Ê‰˚È ËÁ ÍÓÚÓ-

˚ı Ì‡Á˚‚‡ÂÚÒﬂ ˝ÎÂÏÂÌÚÓÏ ÏÌÓÊÂÒÚ‚‡.

èËÏÂ˚ ÏÌÓÊÂÒÚ‚: 1) ÏÌÓÊÂÒÚ‚Ó ÒÚÛ‰ÂÌÚÓ‚, Ó·Û˜‡˛˘ËıÒﬂ ‚

‚ÛÁÂ ‚ ‰‡ÌÌ˚È ÏÓÏÂÌÚ ÔÓ ÒÔÂˆË‡Î¸ÌÓÒÚË 22.03 “Ä‚ÚÓÏ‡ÚËÁË-

Ó‚‡ÌÌ˚Â ÒËÒÚÂÏ˚ Ó·‡·ÓÚÍË ËÌÙÓÏ‡ˆËË Ë ÛÔ‡‚ÎÂÌËﬂ”;

2) ÏÌÓÊÂÒÚ‚Ó ﬂ˜ÂÂÍ ÓÔÂ‡ÚË‚ÌÓÈ Ô‡ÏﬂÚË ùÇå; 3) ÏÌÓÊÂÒÚ‚Ó

ÏÓÏÂÌÚÓ‚ ÓÚÍ‡ÁÓ‚ Ë ‚ÓÒÒÚ‡ÌÓ‚ÎÂÌËÈ ùÇå Á‡ ‚ÂÏﬂ ÂÂ ‡·ÓÚ˚ ‚

ÚÂ˜ÂÌËÂ ÓÔÂ‰ÂÎÂÌÌÓ„Ó ‚ÂÏÂÌË t; 4) ÏÌÓÊÂÒÚ‚Ó ÚÓ˜ÂÍ, ÎÂÊ‡-

˘Ëı ‚ÌÛÚË ¯‡‡ ‡‰ËÛÒ‡ r; 5) ÏÌÓÊÂÒÚ‚Ó ÚÓ˜ÂÍ Ì‡ ÔÎÓÒÍÓÒÚË,

‡ÒÒÚÓﬂÌËÂ ÓÚ ÍÓÚÓ˚ı ‰Ó ÚÓ˜ÍË ‡ Ò ÍÓÓ‰ËÌ‡Ú‡ÏË x

, y

Ì‡

ÔÎÓÒÍÓÒÚË ÌÂ ÔÂ‚˚¯‡ÂÚ ‚ÂÎË˜ËÌ˚ d.

å˚ ‚Ë‰ËÏ, ˜ÚÓ ˝ÎÂÏÂÌÚ˚, ËÁ ÍÓÚÓ˚ı ÒÓÒÚÓﬂÚ ÏÌÓÊÂÒÚ‚‡,

ÏÓ„ÛÚ ËÏÂÚ¸ Ò‡ÏÛ˛ ‡ÁÎË˜ÌÛ˛ ÔËÓ‰Û. ç‡ÔËÏÂ, ÏÌÓÊÂÒÚ‚Ó

ÒÚÛ‰ÂÌÚÓ‚ ÒÓÒÚÓËÚ ËÁ ˛ÌÓ¯ÂÈ Ë ‰Â‚Û¯ÂÍ.

Ñ‡ÎÂÂ, ÍÓÎË˜ÂÒÚ‚Ó ˝ÎÂÏÂÌÚÓ‚, ÒÓÒÚ‡‚Îﬂ˛˘Ëı ÏÌÓÊÂÒÚ‚Ó,

ÏÓÊÂÚ ·˚Ú¸ Ó„‡ÌË˜ÂÌÌ˚Ï (ÏÌÓÊÂÒÚ‚Ó ﬂ˜ÂÂÍ ÓÔÂ‡ÚË‚ÌÓÈ Ô‡-

ÏﬂÚË ùÇå) Ë ÌÂÓ„‡ÌË˜ÂÌÌ˚Ï (ÏÌÓÊÂÒÚ‚Ó ÚÓ˜ÂÍ, ÎÂÊ‡˘Ëı

‚ÌÛÚË ¯‡‡ ‡‰ËÛÒ‡ r).

åÌÓÊÂÒÚ‚Ó Ï˚ ·Û‰ÂÏ Ó·ÓÁÌ‡˜‡Ú¸ ÎË·Ó Ô ÓÔËÒÌ˚ÏË ·ÛÍ‚‡ÏË

Î‡ÚËÌÒÍÓ„Ó ‡ÎÙ‡‚ËÚ‡, ÎË·Ó ÔÂÂ˜ËÒÎÂÌËÂÏ ‚ÒÂı ˝ÎÂÏÂÌÚÓ‚

ÏÌÓÊÂÒÚ‚‡ ‚ ÙË„ÛÌ˚ı ÒÍÓ·Í‡ı, ÎË·Ó ÛÍ‡Á‡ÌËÂÏ (‚ ÚÂı ÊÂ

ÙË„ÛÌ˚ı ÒÍÓ·Í‡ı) Ô‡‚ËÎ‡, ÔÓ ÍÓÚÓÓÏÛ ˝ÎÂÏÂÌÚ ÓÚÌÓÒËÚÒﬂ Í

ÏÌÓÊÂÒÚ‚Û. ë‡ÏË ˝ÎÂÏÂÌÚ˚ ·Û‰ÂÏ Ó·ÓÁÌ‡˜‡Ú¸ ÎË·Ó Ï‡Î˚ÏË ·ÛÍ-

‚‡ÏË Î‡ÚËÌÒÍÓ„Ó ‡ÎÙ‡‚ËÚ‡, ÎË·Ó ÒÎÓ‚ÂÒÌÓ.

ê‡ÒÒÏÓÚËÏ ÌÂÍÓÚÓÓÂ ÏÌÓÊÂÒÚ‚Ó Ä Ë ˝ÎÂÏÂÌÚ ‡, Ô ËÌ‡‰ÎÂ-

Ê‡˘ËÈ ˝ÚÓÏÛ ÏÌÓÊÂÒÚ‚Û. ùÚÓ ÛÚ‚ÂÊ‰ÂÌËÂ: ˝ÎÂÏÂÌÚ ‡ ÔËÌ‡‰-

ÎÂÊËÚ ÏÌÓÊÂÒÚ‚Û Ä, ·Û‰ÂÏ ÒËÏ‚ÓÎË˜ÂÒÍË Á‡ÔËÒ˚‚‡Ú¸ Ú‡Í:

‡ [ A (ËÎË Ä ] ‡). (1.1)

é·‡ÚÌÓÂ ÛÚ‚ÂÊ‰ÂÌËÂ: ˝ÎÂÏÂÌÚ ‡ ÌÂ ÔËÌ‡‰ÎÂÊËÚ Ä, Á‡-

ÔË¯ÂÏ ÒÎÂ‰Û˛˘ËÏ Ó·‡ÁÓÏ

a [ A (ËÎË Ä ] ‡). (1.2)

èË‚Â‰ÂÏ ÔËÏÂ˚ Á‡ÔËÒË ‡ÁÎË˜Ì˚ı ÏÌÓÊÂÒÚ‚.

è  Ë Ï Â  1. åÌÓÊÂÒÚ‚Ó ÒÚÛ‰ÂÌÚÓ‚ S, Ó·Û˜‡˛˘ËıÒﬂ ‚ ‚ÛÁÂ ‚

‰‡ÌÌ˚È ÏÓÏÂÌÚ ÔÓ ÒÔÂˆË‡Î¸ÌÓÒÚË 22.02, ÏÓÊÂÚ ·˚Ú¸ Á‡‰‡ÌÓ ‚

Ú‡ÍÓÏ ‚Ë‰Â:

S = {s

, s

,..., s

} = {s

; 1 ≤ k ≤ n}, (1.3)

„‰Â n – Ó·˘ÂÂ ˜ËÒÎÓ ÒÚÛ‰ÂÌÚÓ‚ ÒÔÂˆË‡Î¸ÌÓÒÚË 22.02.

è  Ë Ï Â  2. åÌÓÊÂÒÚ‚Ó ﬂ˜ÂÂÍ ÓÔÂ‡ÚË‚ÌÓÈ Ô‡ÏﬂÚË ùÇå

ÏÓÊÌÓ Á‡‰‡Ú¸ Ú‡Í:

å = {0, 1, 2,..., N} = {i – ˆÂÎÓÂ; 0 ≤ i ≤ N}, (1.4)

„‰Â N – Ó·˘ÂÂ ˜ËÒÎÓ ﬂ˜ÂÂÍ ÓÔÂ‡ÚË‚ÌÓÈ Ô‡ÏﬂÚË ùÇå.

è  Ë Ï Â  3. åÌÓÊÂÒÚ‚Ó ÏÓÏÂÌÚÓ‚ ÓÚÍ‡ÁÓ‚ Ë ‚ÓÒÒÚ‡ÌÓ‚ÎÂ-

ÌËÈ ùÇå Á‡ ‚ÂÏﬂ ÂÂ ‡·ÓÚ˚ ‚ ÚÂ˜ÂÌËÂ ‚ÂÏÂÌË t ÏÓÊÂÚ ·˚Ú¸

Á‡‰‡ÌÓ Ú‡Í:

Ä = {i – ˆÂÎÓÂ; i ≥ 0} = {i = 0, 1, 2,..., n,...}. (1.5)

Ç ‰‡ÌÌÓÏ ÒÎÛ˜‡Â ÌÂÚ ‚ÓÁÏÓÊÌÓÒÚË ÛÍ‡Á‡Ú¸ ‚ ÚÓ˜ÌÓÒÚË Ï‡Í-

ÒËÏ‡Î¸ÌÓÂ ˜ËÒÎÓ ÓÚÍ‡ÁÓ‚ Ë ‚ÓÒÒÚ‡ÌÓ‚ÎÂÌËÈ, ÔÓ˝ÚÓÏÛ ÌÂÚ Ó„‡-

ÌË˜ÂÌËÈ Ì‡ ˝ÚÓ ˜ËÒÎÓ.

è  Ë Ï Â  4. åÌÓÊÂÒÚ‚Ó ÚÓ˜ÂÍ, ÎÂÊ‡˘Ëı ‚ Ì Û Ú  Ë ¯‡‡ ‡-

‰ËÛÒ‡ r, ÏÓÊÌÓ Á‡‰‡Ú¸ ‚ Ú‡ÍÓÏ ‚Ë‰Â:

Ç = {x

+ y

+ z

< r

} =

= {x, y, z); x

+ y

+ z

< r

}, (1.6)

„‰Â x, y, z – ‰ÂÍ‡ÚÓ‚˚ ÍÓÓ‰ËÌ‡Ú˚ ÚÓ˜ÍË (Ì‡˜‡ÎÓ ÍÓÓ‰ËÌ‡Ú

ÒÓ‚Ô‡‰‡ÂÚ Ò ˆÂÌÚÓÏ ¯‡‡); ËÎË Ú‡Í:

Ç = {0 ≤ α ≤ 2π; 0 ≤ β ≤ 2π; ρ < r}, (1.7)

„‰Â α , β, ρ – ÔÓÎﬂÌ˚Â ÍÓÓ‰ËÌ‡Ú˚ ÚÓ˜ÍË (ÚÓ ÊÂ ÔË ÛÒÎÓ‚ËË

ÒÓ‚Ô‡‰ÂÌËﬂ Ì‡˜‡Î‡ ÍÓÓ‰ËÌ‡Ú Ò ˆÂÌÚÓÏ ¯‡‡).

è  Ë Ï Â  5. åÌÓÊÂÒÚ‚Ó ÚÓ˜ÂÍ, ÔËÌ‡‰ÎÂÊ‡˘Ëı Ò Ù Â  Â

‡‰ËÛÒ‡ r, ÏÓÊÌÓ Á‡‰‡Ú¸ ÒÎÂ‰Û˛˘ËÏ Ó·‡ÁÓÏ:

ë = {x

+ y

+ z

= r

} = {(x, y, z); x

+ y

+ z

= r

} =

= {0 ≤ α ≤ 2π; 0 ≤ β ≤ 2π; ρ = r}, (1.8)

„‰Â x, y, z; α, β, ρ ÓÚ‚Â˜‡˛Ú ÚÂÏ ÊÂ ÚÂ·Ó‚‡ÌËﬂÏ, ˜ÚÓ Ë ‰Îﬂ

ÙÓÏÛÎ (1.5), (1.7).

è  Ë Ï Â  6. åÌÓÊÂÒÚ‚Ó ÚÓ˜ÂÍ Ì‡ ÔÎÓÒÍÓÒÚË, ‡ÒÒÚÓﬂÌËÂ ÓÚ

ÍÓÚÓ˚ı ‰Ó ÚÓ˜ÍË ‡ (Ò ‰ÂÍ‡ÚÓ‚˚ ÏË ÍÓÓ‰ËÌ‡Ú‡ÏË x

, y

Ì‡

˝ÚÓÈ ÔÎÓÒÍÓÒÚË) ÌÂ ÔÂ‚˚¯‡ÂÚ ‚ÂÎË˜ËÌ˚ d, ÏÓÊÌÓ Á‡‰‡Ú¸ Ú‡Í:

Dxxyyd

= − + − <













()()

(1.9)

ËÎË ‚ ÔÓÎﬂÌ˚ı ÍÓÓ‰ËÌ‡Ú‡ı

= −− − <













ρρ ρρ αα

2 cos( ) , (1.10)

„‰Â α

‡

, ρ

‡

– ÔÓÎﬂÌ˚Â ÍÓÓ‰ËÌ‡Ú˚ ÚÓ˜ÍË ‡. ➤

åÌÓÊÂÒÚ‚Ó Ç Ì‡Á˚‚‡ÂÚÒﬂ ÔÓ‰ÏÌÓÊÂÒÚ‚ÓÏ (˜‡ÒÚ¸˛) ÏÌÓÊÂ-

ÒÚ‚‡ Ä, ÂÒÎË ‚ÒÂ ˝ÎÂÏÂÌÚ˚ ÏÌÓÊÂÒÚ‚‡ Ç ÒÓ‰ÂÊ‡ÚÒﬂ Ú‡ÍÊÂ Ë ‚

ÏÌÓÊÂÒÚ‚Â Ä, Ë Ó·ÓÁÌ‡˜‡ÂÚÒﬂ Ú‡Í:

Ç ⊂ Ä (ËÎË Ä ⊃ Ç). (1.11)

ÖÒÎË Í‡Ê‰˚È ˝ ÎÂÏÂÌÚ ÏÌÓÊÂÒÚ‚‡ Ç ÔËÌ‡‰ÎÂÊËÚ ÏÌÓÊÂÒÚ‚Û

Ä Ë Í‡Ê‰˚È ˝ÎÂÏÂÌÚ ÏÌÓÊÂÒÚ‚‡ Ä ÔËÌ‡‰ÎÂÊËÚ ÏÌÓÊÂÒÚ‚Û Ç,

ÚÓ ËÏÂÂÚ ÏÂÒÚÓ ‡‚ÂÌÒÚ‚Ó ‰‚Ûı ÏÌÓÊÂÒÚ‚: Ä = Ç. Ç ˝ÚÓÏ ÒÎÛ-

˜‡Â Ä ⊂ Ç Ë Ç ⊂ Ä.

è  Ë Ï Â  7. åÌÓÊÂÒÚ‚Ó M

‚ÒÂı Á‡ÌﬂÚ˚ı ﬂ˜ÂÂÍ ÓÔÂ‡ÚË‚-

ÌÓÈ Ô‡ÏﬂÚË ùÇå ‚ ‰‡ÌÌ˚È ÏÓÏÂÌÚ ‚ÂÏÂÌË t ﬂ‚ÎﬂÂÚÒﬂ ÔÓ‰-

ÏÌÓÊÂÒÚ‚ÓÏ ‚ÒÂı ﬂ˜ÂÂÍ ÓÔÂ‡ÚË‚ÌÓÈ Ô‡ÏﬂÚË å:

⊂ M. (1.12)

ÖÒÎË ‚ ÏÓÏÂÌÚ ‚ÂÏÂÌË t ‚ÒÂ ﬂ˜ÂÈÍË ÓÔÂ‡ÚË‚ÌÓÈ Ô‡ÏﬂÚË

Á‡ÌﬂÚ˚ , ÚÓ ËÏÂÂÚ ÏÂÒÚÓ ‡‚ÂÌÒÚ‚Ó

= M. (1.13)➤

ÑÛ„ËÏË ÒÎÓ‚‡ÏË, ‰‚‡ ÏÌÓÊÂÒÚ‚‡ Ä Ë Ç ÒÓ‚Ô‡‰‡˛Ú (ËÎË

‡‚Ì˚): Ä = Ç, ÂÒÎË ÓÌË ÒÓÒÚÓﬂÚ ËÁ Ó‰ÌËı Ë ÚÂı ÊÂ ˝ÎÂÏÂÌ-

ÚÓ‚. åÌÓÊÂÒÚ‚Ó, ÌÂ ÒÓ‰ÂÊ‡˘ÂÂ ÌË Ó‰ÌÓ„Ó ˝ÎÂÏÂÌÚ‡, Ì‡Á˚‚‡ÂÚ-

Òﬂ ÔÛÒÚ˚Ï ÏÌÓÊÂÒÚ‚ÓÏ Ë Ó·ÓÁÌ‡˜‡ÂÚÒﬂ ∅. ÇÒﬂÍÓÂ ÏÌÓÊÂÒÚ‚Ó

ÒÓ‰ÂÊËÚ ‚ Í‡˜ÂÒÚ‚Â Ò‚ÓÂ„Ó ÔÓ‰ÏÌÓÊÂÒÚ‚‡ ÔÛÒÚÓÂ ÏÌÓÊÂÒÚ‚Ó ∅.

è  Ë Ï Â  8. åÌÓÊÂÒÚ‚Ó ÚÓ˜ÂÍ x, y ÔﬂÏÓÈ, Û‰Ó‚ÎÂÚ‚Óﬂ˛-

˘Ëı ÛÒÎÓ‚Ë˛ x – y < 0, ﬂ‚ÎﬂÂÚÒﬂ ÔÛÒÚ˚Ï:

{x – y < 0} = ∅.

ÖÒÚÂÒÚ‚ÂÌÌÓ, ˜ÚÓ ‚ÒÂ ÔÛÒÚ˚Â ÏÌÓÊÂÒÚ‚‡ ‡‚Ì˚ ÏÂÊ‰Û ÒÓ·ÓÈ.

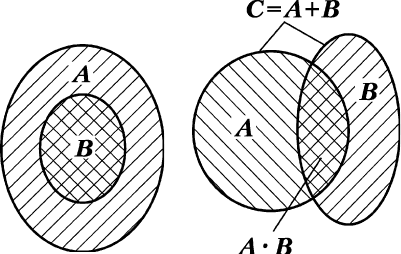
ÑÎﬂ Ì‡„Îﬂ‰ÌÓÒÚË Ï˚ ·Û‰ÂÏ ËÁÓ·‡Ê‡Ú¸ ÏÌÓÊÂÒÚ‚‡ ‚ ‚Ë‰Â Í‡-

ÍËı-ÎË·Ó ÙË„Û Ì‡ ÔÎÓÒÍÓÒÚË (ËÒ. 1.1), „‰Â ˝ÎÂÏÂÌÚ‡ÏË ÏÌÓ-

ÊÂÒÚ‚‡ ﬂ‚Îﬂ˛ÚÒﬂ ÚÓ˜ÍË Ì‡ ÔÎÓÒÍÓÒÚË, ÔËÌ‡‰ÎÂÊ‡˘ËÂ ˝ÚËÏ

ÙË„Û‡Ï. í‡Í, Ì‡ ËÒ. 1.1 Í‡Ê‰‡ﬂ ÚÓ˜Í‡ ÙË„Û˚ Ç ÔËÌ‡‰ÎÂ-

ÊËÚ Ó‰ÌÓ‚ÂÏÂÌÌÓ Ë ÙË„ÛÂ Ä, ÔÓ˝ÚÓÏÛ ÒÔ‡‚Â‰ÎË‚Ó ÒÓÓÚÌÓ-

¯ÂÌËÂ Ç ⊂ Ä. é‰Ì‡ÍÓ ‡‚ÂÌÒÚ‚Ó ÏÂÊ‰Û ÏÌÓÊÂÒÚ‚‡ÏË Ä Ë Ç ÌÂ

ËÏÂÂÚ ÏÂÒÚ‡.

ê‡ÒÒÏÓÚËÏ ‡ÁÎË˜Ì˚Â ÓÔÂ‡ˆËË Ì‡‰ ÏÌÓÊÂÒÚ‚‡ÏË.

ëÛÏÏÓÈ (ËÎË Ó·˙Â‰ËÌÂÌËÂÏ) ÏÌÓÊÂÒÚ‚ Ä Ë Ç Ì‡Á˚‚‡ÂÚÒﬂ

ÏÌÓÊÂÒÚ‚Ó ë = Ä + Ç (ËÎË ë = A∪ B), ˝ÎÂÏÂÌÚ˚ ÍÓÚÓÓ„Ó

ÔËÌ‡‰ÎÂÊ‡Ú ËÎË ÏÌÓÊÂÒÚ‚Û Ä, ËÎË ÏÌÓÊÂÒÚ‚Û Ç (‰Û„ËÏË

ÒÎÓ‚‡ÏË: ˝ÎÂÏÂÌÚ˚ ÏÌÓÊÂÒÚ‚‡ ë ÔËÌ‡‰ÎÂÊ‡Ú ıÓÚﬂ ·˚ Ó‰ÌÓÏÛ

ËÁ ÏÌÓÊÂÒÚ‚ Ä Ë Ç).

ç‡ ËÒ. 1.2 ÔÓÍ‡Á‡Ì‡ „ÂÓÏÂÚË˜ÂÒÍ‡ﬂ ËÌÚÂÔÂÚ‡ˆËﬂ ÒÛÏÏ˚

‰‚Ûı ÏÌÓÊÂÒÚ‚: Ä + Ç = ë, ÍÓÚÓ‡ﬂ ÔÂ‰ÒÚ‡‚ÎﬂÂÚ ÒÓ·ÓÈ ÏÌÓÊÂ-

ÒÚ‚Ó ÚÓ˜ÂÍ, ÔËÌ‡‰ÎÂÊ‡˘Ëı ‚ÒÂÈ Á‡¯ÚËıÓ‚‡ÌÌÓÈ Ó·Î‡Ò-

ÚË: ÌÂ‚‡ÊÌÓ, Á‡¯ÚËıÓ‚‡Ì‡ ÎË ˝Ú‡ Ó·Î‡ÒÚ¸ Ó‰ËÌ ‡Á, ËÎË

‰‚‡Ê‰˚.

àÁ ËÒ. 1.1 ÒÎÂ‰ÛÂÚ, ˜ÚÓ ÂÒÎË Ç ⊂ Ä, ÚÓ Ä + Ç = Ä.

àÁ ËÒ. 1.3 ÒÛÏÏÓÈ ÏÌÓÊÂÒÚ‚ Ä Ë Ç ﬂ‚ÎﬂÂÚÒﬂ ÏÌÓÊÂÒÚ‚Ó ë,

˝ÎÂÏÂÌÚ˚ ÍÓÚÓÓ„Ó ÔËÌ‡‰ÎÂÊ‡Ú Í‡Í ÏÌÓÊÂÒÚ‚Û Ä, Ú‡Í Ë ÏÌÓ-

ÊÂÒÚ‚Û Ç.

êàë. 1.1 êàë. 1.2

è  Ë Ï Â  9. ê‡ÒÒÏÓÚËÏ ÒÛÏÏÛ ‡ÁÎË˜Ì˚ı ÏÌÓÊÂÒÚ‚.

1) {1, 2,..., 50} + {1, 2,..., 80} = {1, 2,..., 80};

2) {1, 2,..., 50} + {25, 26,.., 50,..., 100} = {1, 2,..., 100};

3) {1, 2,..., 50} + {75, 76,..., 100} = {1, 2,..., 50, 75, 76,..., 100};

4) ëÛÏÏ‡ ‰‚Ûı ÏÌÓÊÂÒÚ‚: å – ‚ÒÂı ﬂ˜ÂÂÍ ÓÔÂ‡ÚË‚ÌÓÈ Ô‡Ïﬂ-

ÚË ùÇå (å = {1, 2,..., N) Ë M

– ÏÌÓÊÂÒÚ‚‡ ‚ÒÂı Á‡Ìﬂ Ú˚ı

ﬂ˜ÂÂÍ ÓÔÂ‡ÚË‚ÌÓÈ Ô‡ÏﬂÚË ùÇå ‚ ‰‡ÌÌ˚È ÏÓÏÂÌÚ ‚ÂÏÂÌË t,

‡‚Ì‡

M + M

= M,

Ú‡Í Í‡Í ÏÌÓÊÂÒÚ‚Ó M

ﬂ‚ÎﬂÂÚÒﬂ ÔÓ‰ÏÌÓÊÂÒÚ‚ÓÏ ÏÌÓÊÂÒÚ‚‡ å:

⊆ M. Ç ‰‡ÌÌÓÏ ÒÎÛ˜‡Â ÌÂ ËÒÍÎ˛˜‡ÂÚÒﬂ ‚ÓÁÏÓÊÌÓÒÚ¸ ‡‚ÂÌ-

ÒÚ‚‡ M

= M.

è  Ë Ï Â  10. èÓÍ‡ÊËÚÂ, ˜ÚÓ ÂÒÎË ÏÌÓÊÂÒÚ‚Ó Ç ÔËÌ‡‰ÎÂ-

ÊËÚ ËÎË ‡‚ÌÓ Ä(Ç ⊆ Ä), ÚÓ ËÏÂÂÚ ÏÂÒÚÓ ‡‚ÂÌÒÚ‚Ó

Ä + Ç = Ä. (1.14)

éÚÍÛ‰‡

Ä + Ä = Ä. (1.15)

ëÛÏÏÓÈ Î˛·Ó„Ó (ÍÓÌÂ˜ÌÓ„Ó ËÎË Ò˜ÂÚÌÓ„Ó) ˜ËÒÎ‡ ÏÌÓÊÂÒÚ‚

Ì‡Á˚‚‡ÂÚÒﬂ ÏÌÓÊÂÒÚ‚Ó Ä, Í‡Ê‰˚È ˝ÎÂÏÂÌÚ ÍÓÚÓÓ„Ó ÔËÌ‡‰-

ÎÂÊËÚ ıÓÚﬂ ·˚ Ó‰ÌÓÏÛ ËÁ ÏÌÓÊÂÒÚ‚ Ä

. ÖÒÎË ÒÛÏÏ‡ ÏÌÓÊÂÒÚ‚

ÒÓ‰ÂÊËÚ ÍÓÌÂ˜ÌÓÂ ˜ËÒÎÓ ÒÎ‡„‡ÂÏ˚ı n, ÚÓ

AA AA













∑

ËÎË

. (1.16)

ë˜ÂÚÌ˚Ï ÏÌÓÊÂÒÚ‚ÓÏ ·Û‰ÂÏ Ì‡Á˚‚‡Ú¸ ‚ÒﬂÍÓÂ ÏÌÓÊÂÒÚ‚Ó,

˝ÎÂÏÂÌÚ˚ ÍÓÚÓÓ„Ó ÏÓÊÌÓ ÒÚ‡‚ËÚ¸ ‚Ó ‚Á‡ËÏÌÓ Ó‰ÌÓÁÌ‡˜ÌÓÂ ÒÓ-

ÓÚ‚ÂÚÒÚ‚ËÂ Ò ﬂ‰ÓÏ Ì‡ÚÛ‡Î¸Ì˚ı ˜ËÒÂÎ: 1, 2, 3,.... ë˜ÂÚÌÓÂ

ÏÌÓÊÂÒÚ‚Ó ÒÓ‰ÂÊËÚ ·ÂÒÍÓÌÂ˜ÌÓÂ ˜ËÒÎÓ ˝ÎÂÏÂÌÚÓ‚. íÓ„‰‡, ÂÒÎË

ÒÛÏÏ‡ ÏÌÓÊÂÒÚ‚ ÒÓ‰ÂÊËÚ Ò˜ÂÚÌÓÂ ˜ËÒÎÓ ÒÎ‡„‡ÂÏ˚ı, ÚÓ

AA AA

iri













∞

∑

ËÎË

. (1.17)

êàë. 1.3 êàë. 1.4

è  Ë Ï Â  11. ê‡ÒÒÏÓÚËÏ ÒÛÏÏÛ Ò˜ÂÚÌÓ„Ó ˜ËÒÎ‡ ÏÌÓÊÂÒÚ‚,

Í‡Ê‰ÓÂ ËÁ ÍÓÚÓ˚ı ÒÓ‰ÂÊËÚ Ú Ë ˝ÎÂÏÂÌÚ‡:

{1, 2, 3} + {2, 3, 4} +...+ {n – 1, n, n + 1} +... =

= − +=

∞

∑

{ , , } { , , ,..., ,...},nnn n

11123

Ú.Â. Ï˚ ÔÓÎÛ˜ËÎË ÏÌÓÊÂÒÚ‚Ó Ì‡ÚÛ‡Î¸Ì˚ı ˜ËÒÂÎ.

ç‡È‰ÂÏ ÏÌÓÊÂÒÚ‚Ó, ÔÂ‰ÒÚ‡‚Îﬂ˛˘ÂÂ ÒÛÏÏÛ Ò˜ÂÚÌÓ„Ó ˜ËÒÎ‡

ÏÌÓÊÂÒÚ‚:

{,, } {,, } {,, }nnn nnn nnn

nnn

− += − ++ − +=

∞

= −

∞

= −∞

∞

∑∑∑

11 11 11

= {–2, –1, 0} + {–3, –2, –1} + {–4, –3, –2} +...+ {–1, 0, 1} +

+ {0, 1, 2} + {1, 2, 3} + ... = {..., –n,..., –3, –2, –1, 0, 1, 2,

3,..., n,...},

Ú.Â. Ï˚ ÔÓÎÛ˜ËÏ ÏÌÓÊÂÒÚ‚Ó ‚ÒÂı ˆÂÎ˚ı ˜ËÒÂÎ (ÔÓÎÓÊËÚÂÎ¸Ì˚ı

Ë ÓÚËˆ‡ÚÂÎ¸Ì˚ı, ‚ÍÎ˛˜‡ﬂ 0, ÍÓÚÓÓÂ ÚÓÊÂ ﬂ‚ÎﬂÂÚÒﬂ ˆÂÎ˚Ï

˜ËÒÎÓÏ.

➤

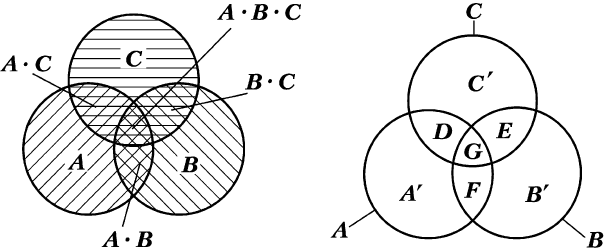
èÂÂÒÂ˜ÂÌËÂÏ (ËÎË ÔÓËÁ‚Â‰ÂÌËÂÏ) ÏÌÓÊÂÒÚ‚ Ä Ë Ç Ì‡Á˚-

‚‡ÂÚÒﬂ ÏÌÓÊÂÒÚ‚Ó D = A

⋅

B (ËÎË Ä∩ Ç), ÒÓÒÚÓﬂ˘ÂÂ ËÁ ˝ÎÂÏÂÌ-

ÚÓ‚, ÔËÌ‡‰ÎÂÊ‡˘Ëı Í‡Í ÏÌÓÊÂÒÚ‚Û Ä, Ú‡Í Ë ÏÌÓÊÂÒÚ‚Û Ç (ÒÏ.

‰‚‡Ê‰˚ Á‡¯ÚËıÓ‚‡ÌÌÛ˛ ÙË„ÛÛ Ì‡ ËÒ. 1.4).

è  Ë Ï Â  12. èÂÂÒÂ˜ÂÌËÂÏ ÏÌÓÊÂÒÚ‚‡ Ä ‚ÒÂı ÒÚÛ‰ÂÌÚÓ‚

ÒÔÂˆË‡Î¸ÌÓÒÚË 22.02, Ó·Û˜‡˛˘ËıÒﬂ Ì‡ ıÓÓ¯Ó Ë ÓÚÎË˜ÌÓ, Ë

ÏÌÓÊÂÒÚ‚‡ ‚ÒÂı ÒÚÛ‰ÂÌÚÓ‚ ˝ÚÓÈ ÊÂ ÒÔÂˆË‡Î¸ÌÓÒÚË, ÔÓÊË‚‡˛-

˘Ëı ‚ Ó·˘ÂÊËÚËË, ·Û‰ÂÚ ÏÌÓÊÂÒÚ‚Ó ÒÚÛ‰ÂÌÚÓ‚ ÒÔÂˆË‡Î¸ÌÓÒÚË

22.02, Ó·Û˜‡˛˘ËıÒﬂ Ì‡ ıÓÓ¯Ó Ë ÓÚÎË˜ÌÓ Ë ÔÓÊË‚‡˛˘Ëı ‚

Ó·˘ÂÊËÚËË.

è  Ë Ï Â  1 3. èÓÍ‡ÊËÚÂ, ˜ÚÓ ÂÒÎË Ç ⊆ Ä, ÚÓ

Ä ⋅ Ç = Ç. (1.18)

àÁ ˝ÚÓ„Ó ÒÎÂ‰ÛÂÚ, ˜ÚÓ

Ä ⋅ Ä = Ä, (1.19)

Ú‡Í Í‡Í Ä = Ä. í‡ÍËÏ Ó·‡ÁÓÏ, Ä + Ä = Ä ⋅ Ä = Ä. èÓÒÎÂ‰-

ÌÂÂ ‡‚ÂÌÒÚ‚Ó Ì‡Á˚‚‡˛Ú Á‡ÍÓÌÓÏ Ë‰ÂÏÔÓÚÂÌÚÌÓÒÚË ‰Îﬂ ÏÌÓ-

ÊÂÒÚ‚. ➤

èÂÂÒÂ˜ÂÌËÂÏ (ËÎË ÔÓËÁ‚Â‰ÂÌËÂÏ) Î˛·Ó„Ó (ÍÓÌÂ˜ÌÓ„Ó ËÎË

Ò˜ÂÚÌÓ„Ó) ˜ËÒÎ‡ ÏÌÓÊÂÒÚ‚ Ä

Ì‡Á˚‚‡ÂÚÒﬂ ÏÌÓÊÂÒÚ‚Ó Ä, Í‡Ê‰˚È

˝ÎÂÏÂÌÚ ÍÓÚÓÓ„Ó ÔËÌ‡‰ÎÂÊËÚ Í‡Ê‰ÓÏÛ ËÁ ÏÌÓÊÂÒÚ‚ A

. èÓ-

ËÁ‚Â‰ÂÌËÂ ÍÓÌÂ˜ÌÓ„Ó ˜ËÒÎ‡ ÏÌÓÊÂÒÚ‚ ·Û‰ÂÏ Ó·ÓÁÌ‡˜‡Ú¸ Í‡Í

AA AA













∏

ËÎË

, (1.20)

„‰Â n – Ó·˘ÂÂ ˜ËÒÎÓ ÔÂÂÏÌÓÊ‡ÂÏ˚ı ÏÌÓÊÂÒÚ‚.

ÑÎﬂ ·ÂÒÍÓÌÂ˜ÌÓ„Ó (Ò˜ÂÚÌÓ„Ó) ˜ËÒÎ‡ ÔÂÂÏÌÓÊ‡ÂÏ˚ı ÏÌÓ-

ÊÂÒÚ‚ ÔÓÎÛ˜ËÏ Ú‡ÍÓÂ ‚˚‡ÊÂÌËÂ:

AA AA













∞

∏

ËÎË

. (1.21)

è  Ë Ï Â  14. èÓÍ‡ÊËÚÂ, ˜ÚÓ ÔÂÂÒÂ˜ÂÌËÂ Ò˜ÂÚÌÓ„Ó ˜ËÒÎ‡

ÏÌÓÊÂÒÚ‚, ‡ÒÒÏÓÚÂÌÌ˚ı ‚ ÔËÏÂ Â 8, ﬂ‚ÎﬂÂÚÒﬂ ÔÛÒÚ˚Ï:

An nn

∞

∏

− +=∅

11{,, }. ➤

ÅÛ‰ÂÏ Ì‡Á˚‚‡Ú¸ ÏÌÓÊÂÒÚ‚‡ Ä Ë Ç ÌÂÔÂÂÒÂÍ‡˛˘ËÏËÒﬂ, ÂÒ-

ÎË ÌË Ó‰ËÌ ˝ÎÂÏÂÌÚ ÏÌÓÊÂÒÚ‚‡ Ä ÌÂ ÔËÌ‡‰ÎÂÊËÚ ÏÌÓÊÂÒÚ‚Û

Ç Ë Ó·‡ÚÌÓ (ÒÏ. ËÒ. 1.3). èÓËÁ‚Â‰ÂÌËÂ (ÔÂÂÒÂ˜ÂÌËÂ) ÌÂÔÂ-

ÂÒÂÍ‡˛˘ËıÒﬂ ÏÌÓÊÂÒÚ‚ ‡‚ÌÓ ÔÛÒÚÓÏÛ ÏÌÓÊÂÒÚ‚Û: Ä ⋅ Ç = ∅.

ìÒÎÓ‚ËÏÒﬂ Ó·ÓÁÌ‡˜‡Ú¸ ÌÂÔÂÂÒÂÍ‡˛˘ËÂÒﬂ ÏÌÓÊÂÒÚ‚‡ Ú‡Í:

Ä ⊄ Ç (ËÎË Ç ⊄ Ä).

è  Ë Ï Â  15. èÓÍ‡ÊËÚÂ, ˜ÚÓ ÔÂÂÒÂ˜ÂÌËÂ ÏÌÓÊÂÒÚ‚‡ Ä ‚ÒÂı

˜ËÒÂÎ, ‰ÂÎﬂ˘ËıÒﬂ Ì‡ 3, Ë ÏÌÓÊÂÒÚ‚‡ Ç ˜ËÒÂÎ, ‰ÂÎﬂ˘Ëı Òﬂ Ì‡ 7,

ﬂ‚ÎﬂÂÚÒﬂ ÏÌÓÊÂÒÚ‚Ó ë ‚ÒÂı ˜ËÒÂÎ, ‰ÂÎﬂ˘ËıÒﬂ Ì‡ 21 ·ÂÁ ÓÒÚ‡Ú-

Í‡. éÚ‚ÂÚ¸ÚÂ Ì‡ ‚ÓÔÓÒ: ﬂ‚ÎﬂÂÚÒﬂ ÎË ÌÛÎ¸ ˝ÎÂÏÂÌÚÓÏ ÏÌÓÊÂÒÚ-

‚‡ ë? ➤

éÔÂ‡ˆËË ÒÎÓÊÂÌËﬂ Ë ÛÏÌÓÊÂÌËﬂ ÏÌÓÊÂÒÚ‚ ÔÓ Ò‚ÓÂÏ ÓÔÂ-

‰ÂÎÂÌË˛ Û‰Ó‚ÎÂÚ‚Óﬂ˛Ú Á‡ÍÓÌ‡Ï ÍÓÏÏÛÚ‡ÚË‚ÌÓÒÚË Ë ‡ÒÒÓˆË-

‡ÚË‚ÌÓÒÚË. ÑÂÈÒÚ‚ËÚÂÎ¸ÌÓ, ‰Îﬂ ÓÔÂ‡ˆËË ÒÎÓÊÂÌËﬂ ÏÌÓÊÂÒÚ‚

ËÏÂÂÏ

ABBA

AB C A BC

+=+

++=++











() ().

(1.22)

Ç ˝ÚÓÏ ÎÂ„ÍÓ Û·Â‰ËÚ¸Òﬂ, ÔÓÎ¸ÁÛﬂÒ¸ „ÂÓÏÂÚË˜ÂÒÍÓÈ ËÌÚÂ-

ÔÂÚ‡ˆËÂÈ ÒÛÏÏ˚ ÏÌÓÊÂÒÚ‚, ËÁÓ·‡ÊÂÌÌ˚ı Ì‡ ËÒ. 1.5. ç‡

˝ÚÓÏ ËÒÛÌÍÂ ÒÛÏÏÓÈ Ä + Ç + ë ﬂ‚ÎﬂÂÚÒﬂ ‚Òﬂ Á‡¯ÚËı Ó‚‡ÌÌ‡ﬂ

Ó·Î‡ÒÚ¸.

ÑÎﬂ ÓÔÂ‡ˆËË ÛÏÌÓÊÂÌËﬂ ÏÌÓÊÂÒÚ‚ ÔÓÎÛ˜ËÏ (ÒÏ. ËÒ. 1.5)

AB BA

AB C A BC

⋅ = ⋅

⋅⋅= ⋅⋅











() ().

(1.23)

äÓÏÂ ÚÓ„Ó, ÓÔÂ‡ˆËË ÒÎÓÊÂÌËﬂ Ë ÛÏÌÓÊÂÌËﬂ ÏÌÓÊÂÒÚ‚

Û‰Ó‚ÎÂÚ‚Óﬂ˛Ú Á‡ÍÓÌÛ ‰ËÒÚË·ÛÚË‚ÌÓÒÚË:

(Ä + Ç) ⋅ C = Ä ⋅ ë + Ç ⋅ ë, (1.24)

Ä ⋅ Ç + ë = (Ä + ë) ⋅ (Ç + ë). (1.25)

ÑÎﬂ ‰ÓÍ‡Á‡ÚÂÎ¸ÒÚ‚‡ ÔÓÒÎÂ‰ÌËı ‰‚Ûı ‡‚ÂÌÒÚ‚ ‚ÓÒÔÓÎ¸ÁÛÂÏÒﬂ

„ÂÓÏÂÚË˜ÂÒÍÓÈ ËÌÚÂÔÂÚ‡ˆËÂÈ, ËÁÓ·‡ÊÂÌÌÓÈ Ì‡ ËÒ. 1.6. ç‡

ËÒ. 1.6 ÏÌÓÊÂÒÚ‚Ó Ä + Ç + ë ‡Á·ËÚÓ Ì‡ ÔÂÂÒÂÍ‡˛˘ËÂÒﬂ

ÔÓ‰ÏÌÓÊÂÒÚ‚‡ Ä′, Ç′, ë′, D, E, F, G; ÓÚÍÛ‰‡

Ä = Ä′ + D + F + G,

Ç = Ç′ + Ö + F + G,

C = C′ + D + E + G.

ëÎÂ‰Ó‚‡ÚÂÎ¸ÌÓ (ÒÏ. ÒÓÓÚÌÓ¯ÂÌËﬂ (1.24)),

(A + B) ⋅ C = [(A′ + D + F + G) + (B′ + E + F + G)] ⋅ C =

= (A′ + D + F + G + B′ + E) ⋅ C = D + G + E, (1.26)

Ú‡Í Í‡Í ë ⋅ Ä′ = ë ⋅ F = C ⋅ B′ = ∅ Ë C ⋅ D = D; ë ⋅ G = G;

B ⋅ C = E + G, Ú‡Í Í‡Í D ⊂ C; G ⊂ C; E ⊂ C. ë ‰Û„ÓÈ ÒÚÓ-

ÓÌ˚,

⋅

C = D + G; B

⋅

C = E + G, (1.27)

ÓÚÍÛ‰‡

⋅

C + B

⋅

ë = D + G + E + G, (1.28)

Ú‡Í Í‡Í G + G = G.

êàë. 1.5 êàë. 1.6

ë‡‚ÌË‚‡ﬂ ‚˚‡ÊÂÌËﬂ (1.26) Ë (1.28), Ï˚ Û·ÂÊ‰‡ÂÏÒﬂ ‚

ÒÔ‡‚Â‰ÎË‚ÓÒÚË ‡‚ÂÌÒÚ‚‡ (1.24).

è  Ë Ï Â  1 6. ÑÓÍ‡ÊËÚÂ Ò‡ÏÓÒÚÓﬂÚÂÎ¸ÌÓ Ò ÔÓÏÓ˘¸˛ „ÂÓÏÂÚ-

Ë˜ÂÒÍÓÈ ËÌÚÂÔÂÚ‡ˆËË ‡‚ÂÌÒÚ‚Ó (1.25). ➤

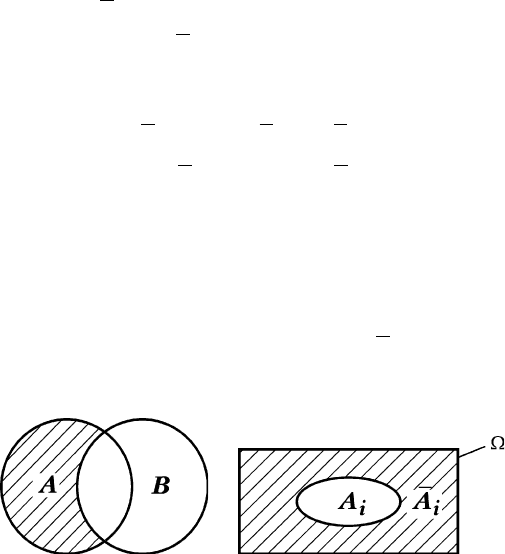
ê‡ÁÌÓÒÚ¸˛ ÏÌÓÊÂÒÚ‚ Ä Ë Ç Ì‡Á˚‚‡ÂÚÒﬂ ÏÌÓÊÂÒÚ‚Ó E = A –

– B (ËÎË E = A\B), ˝ÎÂÏÂÌÚ˚ ÍÓÚÓÓ„Ó ÒÓ‰ÂÊ‡ÚÒﬂ ‚ Ä, ÌÓ ÌÂ

ÒÓ‰ÂÊ‡ÚÒﬂ ‚ Ç (ÒÏ. Á‡¯ÚËı Ó‚‡ÌÌÛ˛ Ó·Î‡ÒÚ¸ Ì‡ ËÒ. 1.7). àÁ

˝ÚÓ„Ó ÓÔÂ‰ÂÎÂÌËﬂ ÒÎÂ‰ÛÂÚ, ˜ÚÓ ÂÒÎË ÏÌÓÊÂÒÚ‚‡ Ä Ë Ç Ì Â Ô Â -

 Â Ò Â Í ‡ ˛ Ú Ò ﬂ (ÒÏ. ËÒ. 1.3), ÚÓ Ä – Ç = Ä Ë Ç – Ä = Ç.

Ç ‰‡Î¸ÌÂÈ¯ÂÏ, ÔË ËÁÛ˜ÂÌËË ÚÂÓËË ‚ÂÓﬂÚÌÓÒÚÂÈ, Ì‡Ï

ÔË‰ÂÚÒﬂ ‡ÒÒÏ‡ÚË‚‡Ú¸ ÏÌÓÊÂÒÚ‚‡ Ä

, Ä

,..., ÍÓÚÓ˚Â ‚ÒÂ ﬂ‚-

Îﬂ˛ÚÒﬂ ÔÓ‰ÏÌÓÊÂÒÚ‚‡ÏË ÌÂÍÓÚÓÓ„Ó ÏÌÓÊÂÒÚ‚‡ Ω:

⊆ Ω. (1.29)

çÂ ËÒÍÎ˛˜‡ÂÚÒﬂ Ë ÒÎÛ˜‡È, ÍÓ„‰‡ Ó‰ÌÓ ËÁ ÔÓ‰ÏÌÓÊÂÒÚ‚  ‡‚ÌÓ

‚ÒÂÏÛ ÏÌÓÊÂÒÚ‚Û Ω (Ä

= Ω).

ê‡ÁÌÓÒÚ¸ Ω – A

Ì‡Á˚‚‡ÂÚÒﬂ ‰ÓÔÓÎÌÂÌËÂÏ ÔÓ‰ÏÌÓÊÂÒÚ‚‡ Ä

Ë Ó·ÓÁÌ‡˜‡ÂÚÒﬂ

ÄA

= −Ω . (1.30)

ç‡ ËÒ. 1.8 Á‡¯ÚËıÓ‚‡ÌÌ‡ﬂ ˜‡ÒÚ¸ ÔÂ‰ÒÚ‡‚ÎﬂÂÚ ÒÓ·ÓÈ ‰Ó-

ÔÓÎÌÂÌËÂ ÔÓ‰ÏÌÓÊÂÒÚ‚‡ A

. àÁ ˝ÚÓ„Ó ÓÔÂ‰ÂÎÂÌËﬂ ÒÎÂ‰ÛÂÚ, ˜ÚÓ

AA A A A

ii i i i

⋅ = ∅ += ⊆;;. ΩΩ

Ñ‡ÎÂÂ, ÂÒÎË A

= Ω, ÚÓ

= ∅, Ú‡Í Í‡Í

= Ω – A

= Ω – Ω=

= ∅.

Ç ‰‡Î¸ÌÂÈ¯ÂÏ Ì‡Ï ÔÓÚÂ·ÛÂÚÒﬂ ËÒÔÓÎ¸ÁÓ‚‡Ú¸ ÔËÌˆËÔ ‰‚ÓÈ-

ÒÚ‚ÂÌÌÓÒÚË, ÍÓÚÓ˚È ‚˚ ÚÂÍ‡ÂÚ ËÁ ÒÎÂ‰Û˛˘Ëı ‰‚Ûı ÒÓÓÚÌÓ¯Â-

ÌËÈ:

1. ÑÓÔÓÎÌÂÌËÂ ÒÛÏÏ˚ ÔÓ‰ÏÌÓÊÂÒÚ‚ A

⊆ Ω), ‡‚ÌÓ ÔÓ-

ËÁ‚Â‰ÂÌË˛ ‰ÓÔÓÎÌÂÌËÈ ˝ÚËı ÔÓ‰ÏÌÓÊÂÒÚ‚:

ΩΩ− = − =

∏∏

∑

AAÄ

iii

( ) . (1.31)

êàë. 1.7 êàë. 1.8