Овчаров Л.А. и др. Математические модели информационых процессов и управления
Подождите немного. Документ загружается.

68
èË Ó·˙‰ËÌÂÌËË ‰‚Ûı „‡ÙÓ‚ ˝ÎÂÏÂÌÚ˚ Ëı χÚˈ ÒÏÂÊ-
ÌÓÒÚË Îӄ˘ÂÒÍË ÒÛÏÏËÛ˛ÚÒfl.
èÂÂÒ˜ÂÌ˲ „‡ÙÓ‚ G
1
∩G
2
ÒÓÓÚ‚ÂÚÒÚ‚ÛÂÚ Îӄ˘ÂÒÍÓÂ
(·Û΂Ó) ÛÏÌÓÊÂÌË Ëı χÚˈ ÒÏÂÊÌÓÒÚË
A(G
1
∩G
2
) = A(G
1
)∧(G
2
) = A
1
∧
A
2
.
èÓÒΉÌflfl χÚˈ‡ ÒÓÒÚÓËÚ ËÁ ÔÓËÁ‚‰ÂÌËÈ
aaa
ij ij ij
() () ()
.
1 2 1 2∧
= ∧
èË ÔÂÂÒ˜ÂÌËË ‰‚Ûı „‡ÙÓ‚ ˝ÎÂÏÂÌÚ˚ Ëı χÚˈ ÒÏÂÊÌÓÒÚË
Îӄ˘ÂÒÍË ÔÂÂÏÌÓʇ˛ÚÒfl ‰Û„ ̇ ‰Û„‡.
í‡Í Í‡Í X
1
⊕X
2
= (X
1
∨X
2
) – (X
1
∧X
2
), ÚÓ ÏÓÊÌÓ ÓÔ‰ÂÎËÚ¸
ÒËÏÏÂÚ˘ÂÒÍÛ˛ ‡ÁÌÓÒÚ¸ ‰‚Ûı ÏÌÓÊÂÒÚ‚, Ó·ÓÁ̇˜‡ÂÏÛ˛ ÒËÏ‚Ó-
ÎÓÏ ç:
M
1
ç M
2
= (M
1
∪M
2
) – (M
1
∩M
2
).
èÓ‰ ÒËÏÏÂÚ˘ÂÒÍÓÈ ‡ÁÌÓÒÚ¸˛ ‰‚Ûı „‡ÙÓ‚ G
1
Ë G
2
ÔÓÌË-
χ˛Ú „‡Ù
G
1
ç G
2
= (G
1
∩
G
2
)∪(
G
1
∩G
2
),
ÍÓÚÓÓÏÛ Óڂ˜‡ÂÚ Ï‡Úˈ‡ ÒÏÂÊÌÓÒÚË
A(G
1
ç G
2
) = A(G
1
) ⊕A(G
2
)
Ò ˝ÎÂÏÂÌÚ‡ÏË
a
ij
(1ç
2)
= ⊕aa
ij ij
() ( )
.
1 2
ëÎÓÊÂÌË ÔÓ ÏÓ‰Ûβ ‰‚Ûı ˝ÎÂÏÂÌÚÓ‚ ‰‚Ûı χÚˈ ‰‡ÂÚ Ï‡Ú-
ËˆÛ ÒÏÂÊÌÓÒÚË „ ‡Ù‡ – ÒËÏÏÂÚ˘ÂÒÍÓÈ ‡ÁÌÓÒÚË. Ç „‡Ù
G
1
ç G
2
‚ıÓ‰flÚ ÚÓθÍÓ Â·‡ G
1
, Ì ‚ıÓ‰fl˘Ë ‚ G
2
, Ë Â·‡
G
2
, Ì ‚ıÓ‰fl˘Ë ‚ G
1
. éÌ fl‚ÎflÂÚÒfl Ó·˙‰ËÌÂÌËÂÏ ÌÂÓ·˘Ëı ˜‡Ò-
ÚÂÈ „‡ÙÓ‚ G
1
Ë G
2
.
è˂‰ÂÏ ÍÓÌÍÂÚÌ˚È ÔËÏÂ.
è Ë Ï Â 1. èÓÒÚÓËÚ¸ χÚˈ˚ Ó·˙‰ËÌÂÌËfl, ÔÂÂÒ˜ÂÌËfl
Ë ÏÓ‰ÛθÌÓÈ ÒÛÏÏ˚
1 234 5 2367
1
2
3
4
5
0 1 001
1 0 11 0
0 1 001
0 1 001
1 0 11 0
2
3
6
7
0 111
1 0 1 0
110 1
1 0 1 0
1 2
AA==
.

69
ê  ¯ Â Ì Ë Â. óÚÓ·˚ ÛÔÓÒÚËÚ¸ ‚˚ÔÓÎÌÂÌË ÓÔ‡ˆËÈ, ÔË‚Â-
‰ÂÏ „‡Ù˚ G
1
Ë G
2
Í Ó·˘ÂÏÛ ÓÒÌÓ‚‡Ì˲ {1, 2, 3, 4, 5, 6, 7}.
0 0
0 0
0 0
0 0
0 0
1 234567 1 234567
1
2
3
4
5
6
7
0 1 001
1 0 110
0 1 001
0 1 001
1 0 110
0000000
0000
1
′
=A
0 0 0 0 0 0 0
0 0 1 0 0 1 1
0 1 0 0 0 1 0
0 0 0 0 0 0 0
0 0 0 0 0 0 0
0 1 1 0 0 0 1
0 1 0 0 0 1 0000
1
2
3
4
5
6
7
2
′
=A
.
å‡Úˈ˚ Ó·˙‰ËÌÂÌËfl Ë ÔÂÂÒ˜ÂÌËfl
′
∨
′
=
′
∧
′
=AA AA
1 2 1 2
0 1 001
1 0 110
0 1 001
0 1 001
1 0 110
0 11 0001
0 1 0001 0
0 0
1 1
1 0
0 0
0 0
0 0 0 0 0 0 0
0 0 1 0 0 0 0
0 1 0 0 0 0 0
0 0 0 0 0 0 0
0 0 0 0 0 0 0
0 0 0 0 0 0 0
0 0 0 0 0 0 0
.
å‡ÚˈÂÈ ÒËÏÏÂÚ˘ÂÒÍÓÈ ‡ÁÌÓÒÚË ·Û‰ÂÚ
′
⊕
′
=AA
1 2
0 1 001
1 001 0
00001
0 1 001
1 0 110
0 11 0001
0 1 0001 0
0 0
1 1
1 0
0 0
0 0
.
éÚÏÂÚËÏ ÌÂÍÓÚÓ˚ ÔÓÎÂÁÌ˚ ҂ÓÈÒÚ‚‡ χÚˈ ÒÏÂÊÌÓÒÚË.
í‡Í Í‡Í a
ij
= 1, ÂÒÎË ËÏÂÂÚÒfl Â·Ó {v
i
, v
j
}, ÚÓ ÒÛÏχ ˝ÎÂÏÂÌÚÓ‚
i-È ÒÚÓÍË Ï‡Úˈ˚ Ä ‡‚̇ ÍÓ΢ÂÒÚ‚Û Â·Â, Ë̈ˉÂÌÚÌ˚ı Ò
v
i
, Ú.Â. ÂÂ ÒÚÂÔÂÌË s(v
i
) = s
i
. ë ‰Û„ÓÈ ÒÚÓÓÌ˚, ÒÛÏχ ˝ÎÂÏÂÌ-
ÚÓ‚ j-„Ó ÒÚÓηˆ‡ χÚˈ˚ ÒÏÂÊÌÓÒÚË ‰‡ÂÚ ÍÓ΢ÂÒÚ‚Ó Â·Â
‚ˉ‡ {v
l
, v
j
}, Ú.Â. ÒÌÓ‚‡ ÒÚÂÔÂ̸ s(v
j
) = s
j
.

70
ÑÎfl ÓÔ‰ÂÎÂÌËfl s
i
ÔÓ Ï‡Úˈ ÒÏÂÊÌÓÒÚË Ä Ì‡‰Ó ÔÓ‰Ò˜Ë-
Ú‡Ú¸ ˜ËÒÎÓ Â‰ËÌˈ ‚ i-È ÒÚÓÍ ËÎË ‚ i-Ï ÒÚÓηˆÂ.
àÁ ÔÓÎÛ˜ÂÌÌÓ„Ó Ú‡ÍËÏ Ó·‡ÁÓÏ ÒÓÓÚÌÓ¯ÂÌËfl
ssv a a
i i ij li
l
n
j
n
== =
==
∑∑
() ,
11
ÒÛÏÏËÛfl ÔÓ i ÓÚ 1 ‰Ó n, ÔÓÎÛ˜ËÏ
sam
i
i
n
ij
j
n
i
n
===
∑∑∑
==
111
2,
„‰Â 2m – Û‰‚ÓÂÌÌÓ ˜ËÒÎÓ Â·Â, Ë·Ó Í‡Ê‰ÓÂ Â·Ó {v
i
, v
i
} ‚ıÓ-
‰ËÚ ‚ ÒÛÏÏÛ ÔÓ Í‡Ê‰ÓÏÛ ËÁ ‰‚Ûı Â„Ó ÍÓ̈ӂ. àÁ ˝ÚÓ„Ó Ù‡ÍÚ‡
‚˚‚Ó‰flÚ fl‰ ÒΉÒÚ‚ËÈ.
í Â Ó Â Ï ‡ 4. Ç ÔÓÒÚÓÏ „‡Ù ÍÓ΢ÂÒÚ‚Â ‚¯ËÌ Ì˜ÂÚÌÓÈ
ÒÚÂÔÂÌË ˜ÂÚÌÓ.
ÑÂÈÒÚ‚ËÚÂθÌÓ, ̘ÂÚÌÓ ˜ËÒÎÓ Ì˜ÂÚÌ˚ı ÒÚÂÔÂÌÂÈ, ÒÎÓ-
ÊÂÌÌÓÂ Ò ˜ÂÚÌÓÈ ÒÛÏÓÈ ˜ÂÚÌ˚ı ÒÚÂÔÂÌÂÈ, ‰‡ÎÓ ·˚ ̘ÂÚÌÓÂ
˜ËÒÎÓ. á̇˜ËÚ, ̘ÂÚÌ˚ ÒÚÂÔÂÌË ‰ÓÎÊÌ˚ ‚ıÓ‰ËÚ¸ Ô‡‡ÏË,
˜ÚÓ·˚ Ó·ÂÒÔ˜ËÚ¸ ˜ÂÚÌÓÒÚ¸ ‚ÒÂÈ ÒÛÏÏ˚ ÒÚÂÔÂÌÂÈ ‚¯ËÌ „‡-
Ù‡.
í Â Ó Â Ï ‡ 5. Ç ÔÓÒÚÓÏ „‡ÙÂ Ò n ‚¯Ë̇ÏË (n ≥ 2) ‚ÒÂ-
„‰‡ ÂÒÚ¸ ÔÓ Í‡ÈÌÂÈ Ï ‰‚ ‚¯ËÌ˚ Ò Ó‰Ë̇ÍÓ‚˚ÏË ÒÚÂÔÂ-
ÌflÏË.
ÑÂÈÒÚ‚ËÚÂθÌÓ, ÂÒÎË ·˚ ‚Ò n ‚¯ËÌ˚ ËÏÂÎË ‡Á΢Ì˚Â
ÒÚÂÔÂÌË, ÚÓ ˝ÚËÏË ÒÚÂÔÂÌflÏË ÏÓ„ÎË ·˚ ·˚Ú¸ ÚÓθÍÓ ˜ËÒ· 0, 1,
2,..., n–1 . çÓ ˝ÚÓ„Ó Ì ÏÓÊÂÚ ·˚Ú¸, Ë·Ó Ì‡Î˘Ë ËÁÓÎËÓ‚‡ÌÌÓÈ
‚¯ËÌ˚ (ÒÚÂÔÂÌË 0) ÔÓÚË‚Ó˜ËÚ Ì‡ÎË˜Ë˛ ‚¯ËÌ˚, Ò‚fl-
Á‡ÌÌÓÈ ÒÓ ‚ÒÂÏË ÓÒڇθÌ˚ÏË (ÒÚÂÔÂÌË n–1). ➤
ùÚË ÔÓÒÚ˚ ÚÂÓÂÏ˚ ÔÓÁ‚ÓÎfl˛Ú Á‡ÏÂÚËÚ¸, ˜ÚÓ ‚ „‡ÙÂ, ÒÓ-
ÒÚÓfl˘ÂÏ ËÁ ‚¯ËÌ ÒÚÂÔÂÌË 1 Ë 2, ÍÓ΢ÂÒÚ‚Ó n
1
‚ËÒfl˜Ëı ‚ -
¯ËÌ ‚Ò„‰‡ ˜ÂÚÌÓ: n
1
= 2s, „‰Â s = 0, 1, 2,...,
n
2
. èË n = 2
ËϲÚÒfl ‰‚ ‚ËÒfl˜Ë ‚¯ËÌ˚ Ë m = 1. èË n = 3, ÎË·Ó ÌÂÚ
‚ËÒfl˜Ëı ‚ ¯ËÌ (G = K
3
), ÎË·Ó ÂÒÚ¸ ‰‚ ‚ËÒfl˜ËÂ Ë Ó‰Ì‡ ÔÓ-
fl‰Í‡ 2.
Ç ˆËÍÎÓ‚ÓÏ „‡Ù ÔÓfl‰Í‡ n, Ә‚ˉÌÓ, n
1
= 0, ‡ n
2
= n,
Ú.Â. ‚Ò ‚¯ËÌ˚ ÔÓfl‰Í‡ ‰‚‡.
Ä̇ÎÓ„ χÚˈ˚ ÒÏÂÊÌÓÒÚË ÏÓÊÌÓ ÔÓÒÚÓËÚ¸ Ë ‰Îfl ÏÛθÚË-
„‡Ù‡
˜˜
);G( , VR i-, j-È ˝ ÎÂÏÂÌÚ Ï‡Úˈ˚ ÒÏÂÊÌÓÒÚË ÏÛθÚË„‡-
Ù‡ ÓÔ‰ÂÎfl˛Ú ˜ËÒÎÓÏ Â·Â, ÒÓ‰ËÌfl˛˘Ëı ‚¯ËÌ˚ v
i
Ë v
j
.
é‰Ì‡ÍÓ „ÎÛ·ÓÍËı ÂÁÛθڇÚÓ‚ ڇ͇fl χÚˈ‡ Ì ‰‡ÂÚ.
71
ÑÎfl ÔÓÒÚ˚ı „‡ÙÓ‚ ¯ËÓÍÓ ÔËÏÂÌflÂÚÒfl ‰Û„‡fl χÚˈ‡,
ÔÓÎÛ˜‡˛˘‡flÒfl ËÁ Ú‡·Îˈ˚ Ò ¯‡ÔÍÓÈ r
1
, r
2
,..., r
m
Ë Î‚˚Ï ·ÓÍÓ-
‚ËÍÓÏ v
1
, v
2
,..., v
n
.
èflÏÓÛ„ÓθÌÓ ÚÂÎÓ Ú‡·Îˈ˚ ‡ÁÏÂÌÓÒÚË n×m Ó·‡ÁÛÂÚ
‰‚Ó˘ÌÛ˛ χÚËˆÛ B = [b
ij
], ÓÔËÒ˚‚‡˛˘Û˛ Ë̈ˉÂÌÚÌÓÒÚ¸
‚¯ËÌ Ë Â·Â. Ç Ï‡Úˈ Ë̈ˉÂ̈ËÈ ˝ÎÂÏÂÌÚ b
ij
= 1 ÚÓ„‰‡
Ë ÚÓθÍÓ ÚÓ„‰‡, ÍÓ„‰‡ v
i
Ë̈ˉÂÌÚ̇ Â·Û r
j
. Ç Í‡Ê‰ÓÏ ÒÚÓηˆÂ
χÚˈ˚ B (Óڂ˜‡˛˘ÂÏ Ó‰ÌÓÏÛ Â·Û) ÒÚÓflÚ ‰‚ ‰ËÌˈ˚ ‚
ÒÚÓ͇ı, Óڂ˜‡˛˘Ëı ÍÓ̈‡Ï ˝ÚÓ„Ó Â·‡.
éÚÏÂÚËÏ, ˜ÚÓ ÒÛÏχ ‚ÒÂı n ÒÚÓÍ, ‚ÁflÚ‡fl ÔÓ ÏÓ‰Ûβ ‰‚‡,
‡‚̇ ÌÛβ. ÖÒÎË ‡ÒÒχÚË‚‡Ú¸ ÒÚÓÍË B Í‡Í ‰‚Ó˘Ì˚ ‚ÂÍ-
ÚÓ˚ b
i
‡ÁÏÂÌÓÒÚË m, ÚÓ ÏÂÊ‰Û ÌËÏË ÒÛ˘ÂÒÚ‚ÛÂÚ ÎËÌÂÈ̇fl
Á‡‚ËÒËÏÓÒÚ¸: b
1
⊕ b
2
⊕ b
n
= 0. ê‡Ì„ χÚˈ˚ B ÔÓ˝ÚÓÏÛ Ì ÔÂ-
‚ÓÒıÓ‰ËÚ ˜ËÒ· n–1.
ëÛÏχ ˝ÎÂÏÂÌÚÓ‚ χÚˈ˚ Ë̈ˉÂ̈ËÈ ÔÓ i-È ÒÚÓÍ ‡‚-
̇ ÒÚÂÔÂÌË s(v
i
) = s
i
, ‡ ÒÛÏχ ˝ÎÂÏÂÌÚÓ‚ ÔÓ ÒÚÓηˆÛ ‡‚̇
‰‚ÛÏ.
è Ë Ï Â 2. èÓÒÚÓËÏ Ï‡ÚËˆÛ Ë̈ˉÂ̈ËÈ ‰Îfl „‡Ù‡ G
8
–
“˜ÂÎӂ˜ÂÍ ·ÂÁ ¯ÂË” (ÒÏ. ËÒ. 2.29, ‡). ÑÎfl ˝ÚÓ„Ó “„ÓÎӂ” ͇Í
Â·Û „‡Ù‡ ÔËÔ˯ÂÏ ÌÓÏ 1, “Ô‡‚ÓÈ” ÛÍ – 2, ΂ÓÈ – 3,
ÚÛÎÓ‚Ë˘Û – 4, Ô‡‚ÓÈ ÌÓ„Â – 5 Ë Î‚ÓÈ ÌÓ„Â – 6. èÓÎÛ˜ËÏ Ï‡Ú-
ËˆÛ Ë̈ˉÂ̈ËÈ ‰Îfl “˜ÂÎӂ˜͇”, „‰Â b
11
= 2:
B
˜ÂÎ
2
0
0
0
0
0
1
1
0
0
0
0
1
0
1
0
0
0
1
0
0
1
0
0
0
0
0
1
1
0
0
0
0
1
0
1
= .
å‡Úˈ˚ ‡ÁϘÂÌÌ˚ı Ë ‚Á‚¯ÂÌÌ˚ı „‡ÙÓ‚. éÔ‰ÂÎËÏ
ÔÓÌflÚË ‚Á‚¯ÂÌÌÓ„Ó „‡Ù‡ ‚ ÚÓ˜Ì˚ı ÚÂÏË̇ı. èˉ‡‰ËÏ
͇ʉÓÈ ‚¯ËÌ v
i
„‡Ù‡ G = (V, R) ‚ÂÒ w
i
ËÁ ÏÌÓÊÂÒÚ‚‡ ‚Â-
ÒÓ‚ W. èÓÎÛ˜ÂÌÌ˚ ԇ˚ (v
i
, w
i
) Ó·‡ÁÛ˛Ú ÏÌÓÊÂÒÚ‚Ó V
W
‚Á‚¯ÂÌÌ˚ı ‚¯ËÌ. ëÓÔÓÒÚ‡‚ËÏ Í‡Ê‰ÓÏÛ Â·Û r
j
∈ R ‚ÂÒ l
j
ËÁ ÏÌÓÊÂÒÚ‚‡ ‚ÂÒÓ‚ L. åÌÓÊÂÒÚ‚Ó Ô‡ R
L
= {(r
j
, l
j
), j =
1, m}
Ô‰ÒÚ‡‚ÎflÂÚ Ò˄̇ÚÛ Û ‚Á‚¯ÂÌÌÓ„Ó „‡Ù‡
˜
G = (V
W
, R
L
).
ÑÎfl Á‡‰‡ÌËfl ‚Á‚¯ÂÌÌÓ„Ó „‡Ù‡ ̇‰Ó ÓÔ‰ÂÎËÚ¸ ‰‚ ˜ËÒÎÓ‚˚Â
ÙÛÌ͈ËË, ‚Á‚¯˂‡˛˘Ë ‚¯ËÌ˚ Ë Â·‡ „‡Ù‡ G.
ê‡ÁϘÂÌÌ˚Ï „‡ÙÓÏ Ò˜ËÚ‡ÂÚÒfl Ú‡ÍÓÈ ‚Á‚¯ÂÌÌ˚È „‡Ù, Û
ÍÓÚÓÓ„Ó ‚ÂÒ‡ ‚¯ËÌ Ë Â·Â – Ì ˜ËÒ·, ‡ ͇ÍËÂ-ÚÓ ÒËÏ‚ÓÎ˚,
ÏÂÚÍË.
72
ÑÎfl χÚ˘ÌÓ„Ó Ô‰ÒÚ‡‚ÎÂÌËfl ‚Á‚¯ÂÌÌÓ„Ó „‡Ù‡
˜
,
G
WL
ÚÂ·Û˛ÚÒfl ÚË Ï‡Úˈ˚: χÚˈ‡ ÒÏÂÊÌÓÒÚË ËÒıÓ‰ÌÓ„Ó „‡Ù‡
G A = A(G), χÚˈ‡-ÒÚÓηˆ W
G
‚ÂÒÓ‚ ‚¯ËÌ, ÔÓfl‰ÓÍ ÍÓÚÓ-
ÓÈ n×1, Ë ‰Ë‡„Ó̇θ̇fl χÚˈ‡ ‚ÂÒÓ‚ · L
G
, ÔÓfl‰ÓÍ ÍÓ-
ÚÓÓÈ m×n:
W
w
w
w
wW
n
iG
= ∈
1
2
M
,;
L
l
l
l
lL
m
jG
= ∈
1
2
0
0
O
,.
ÖÒÎË L
G
= ε
m
, ÚÓ ‚ „‡ÙÂ
˜
,
G
WL
·‡ Ì ËÏÂ˛Ú ‚ÂÒÓ‚; ÂÒÎË
‚ÂÒ‡ ‚¯ËÌ W
i
= 1, i = 1, 2,..., n ÚÓ Û
˜
,
G
WL
ÓÚÒÛÚÒÚ‚Û˛Ú ‚ÂÒ‡
‚¯ËÌ.
å‡Úˈ˚ A(G), WG Ë L
G
ÔÓÎÌÓÒÚ¸˛ Ô‰ÒÚ‡‚Îfl˛Ú „‡Ù
˜
,
G
WL
. ÑÎfl Ó„‡ÙÓ‚
r
G ÓÔ‰ÂÎfl˛Ú ‰‚ χÚˈ˚ Ë̈ˉÂÌÚÌÓÒ-
ÚË: B
+
– ‰Îfl ̇˜‡Î¸Ì˚ı ‚¯ËÌ ‰Û„, B
–
– ‰Îfl ÍÓ̘Ì˚ı ‚Â-
¯ËÌ ‰Û„.
b
vr
ij
ij
+
=
1, ÂÒÎË – ̇˜‡ÎÓ ‰Û„Ë
– ‚ ÔÓÚË‚ÌÓÏ ÒÎÛ˜‡Â;
,
0
b
vr
ij
ij
−
=
1, ÂÒÎË – ̇˜‡ÎÓ ‰Û„Ë
– ‚ ÔÓÚË‚ÌÓÏ ÒÎÛ˜‡Â.
,
0
ÖÒÎË ‚ „‡Ù ÌÂÚ ÔÂÚÂθ, ÚÓ Ï‡Úˈ‡ B = B
+
– B
–
‰‡ÂÚ ÔÓÎ-
ÌÛ˛ χÚËˆÛ Ë̈ˉÂ̈ËÈ „‡Ù‡
r
G. ùÎÂÏÂÌÚ ˝ÚÓÈ Ï‡Úˈ˚
b
ij
=
1,
ÂÒÎË v
i
–
̇˜‡ÎÓ r
j
-È ‰Û„Ë, b
ij
= –1, ÂÒÎË
v
i
–
ÍÓ̈ ‰Û„Ë r
j
.
ÑÎfl „‡Ù‡ Ò ÔÂÚÎflÏË Ú·ÛÂÚÒfl Á̇ÌË χÚˈ B
+
Ë B
–
.
å‡Úˈ˚ B (B
+
Ë B
–
‰Îfl „‡Ù‡ Ò ÔÂÚÎflÏË), W
G
Ë L
G
ÔÓÎ-
ÌÓÒÚ¸˛ Á‡‰‡˛Ú ‚Á‚¯ÂÌÌ˚È Ó„‡Ù
˜
,
G
WL
. èË ˝ÚÓÏ Ì‡Ô‡‚ÎÂ-
ÌËfl ÓËÂÌÚ‡ˆËË ‰Û„ Û
r
G Ë
˜
,
G
WL
ÒÓ‚Ô‡‰‡˛Ú. èÂÚÎfl r
i
= (v
i
, v
i
)
ÓÚϘ‡ÂÚÒfl ‰ËÌˈ‡ÏË ˝ÎÂÏÂÌÚ‡ i, j Í‡Í ‚ B
+
, Ú‡Í Ë ‚ B
–
. í‡Í
73
Û˜ËÚ˚‚‡ÂÚÒfl ̇˜‡Î¸ÌÓÒÚ¸ Ë ÍÓ̘ÌÓÒÚ¸ ÔÂÚÎË ÓÚÌÓÒËÚÂθÌÓ
‰Û„Ë r
i
Ò ·ÂÁ‡Á΢ÌÓÈ ÓËÂÌÚ‡ˆËÂÈ.
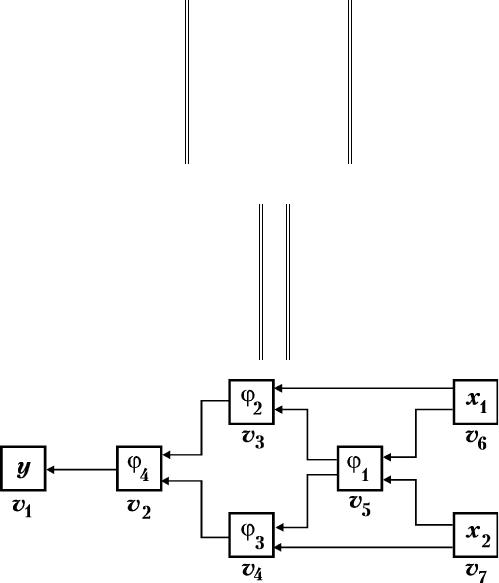
è Ë Ï Â 3. èÓÒÚÓËÚ¸ ‡ÁϘÂÌÌ˚È „‡Ù, Ô‰ÒÚ‡‚Îfl˛-
˘ËÈ ÙÛÌÍˆË˛ ‡Î„·˚ ÎÓ„ËÍË y = ϕ
2
(x
1
, ϕ
1
(x
1
, x
2
)) ⊕ ϕ
3
(ϕ
1
(x
1
,
x
2
)x
2
), Ë Ì‡ÈÚË Â„Ó Ï‡Ú˘ÌÓ ÓÔËÒ‡ÌËÂ.
ê  ¯ Â Ì Ë Â. äÓ΢ÂÒÚ‚Ó ‚¯ËÌ „‡Ù‡ (ÒÏ. ËÒ. 2.31) ‡‚-
ÌÓ ˜ËÒÎÛ ‡Á΢Ì˚ı ÒËÏ‚ÓÎÓ‚ x
1
, x
2
, ϕ
1
, ϕ
2
, ϕ
3
, ⊕ = ϕ
4
, y. ÑÛ„‡,
‚Â‰Û˘‡fl Í v
1
= y, ˉÂÚ ÓÚ ‚¯ËÌ v
2
= ⊕. Ç Ò‚Ó˛ Ә ‰¸ v
2
ÔËÌËχÂÚ ‰Û„Ë ÓÚ v
3
= ϕ
2
Ë v
4
= ϕ
3
, ‡ v
3
– ÓÚ v
5
= ϕ
1
v
6
= x
1
. Ç
‚¯ËÌÛ v
4
‚‰ÛÚ ‰Û„Ë ÓÚ ‚¯ËÌ v
5
= ϕ
1
Ë v
7
= x
2
.
ê‡ÁϘÂÌÌ˚È Ó„‡Ù ËÏÂÂÚ ÌÓÒËÚÂθ
V
W
= {(v
1
, y), (v
2
, ϕ
4
), (v
3
, ϕ
2
), (v
4
, ϕ
3
), (v
5
, ϕ
1
),
(v
6
, x
1
), (v
7
, x
2
)}.
å‡Úˈ‡ ÒÏÂÊÌÓÒÚË Ä ˝ÚÓ„Ó „‡Ù‡ (ÒÏ. ËÒ. 2.31) ËÏÂÂÚ
ÔÓfl‰ÓÍ 7×7:
r
A =
0 0 0 0 0 0 0
0 0 0 0 0 0
0 1 0 0 0 0 0
0 1 0 0 0 0 0
0 0 1 1 0 0 0
0 0 1 0 1 0 0
0 0 0 1 1 0 0
1
.
å‡Úˈ‡ ‚ÂÒÓ‚ ‚¯ËÌ – ÒÚÓηˆ W
G
:
W
y
x
x
G
=
ϕ
ϕ
ϕ
ϕ
4
2
3
4
1
2
.
êàë. 2.31. 鄇٠ÙÛÌ͈ËË

74
å‡Úˈ‡ ‚ÂÒÓ‚ ‰Û„ ‚˚ÓʉÂÌ̇fl, L
G
= ε
m
– ‰ËÌ˘̇fl χÚ-
ˈ‡ ÔÓfl‰Í‡ m×m.
å‡Úˈ‡ Ë̈ˉÂ̈ËÈ B ËÏÂÂÚ ÔÓfl‰ÓÍ 7×9:
r
B =
−
−−
−−
−−
−−
1 00000000
111000000
0 1 0 110000
0 1 000 1100
0001 0 1 0 11
00001 001 0
0000001 0 1
.
àÁ
r
A ÏÓÊÌÓ ÔÓÎÛ˜ËÚ¸ χÚËˆÛ Ä ÒÏÂÊÌÓÒÚË ÒÓÓÚ‚ÂÚÒÚ‚Û˛-
˘Â„Ó ÌÂÓËÂÌÚËÓ‚‡ÌÌÓ„Ó „‡Ù‡, ‰Îfl ˜Â„Ó Ì‡‰Ó ÔÓÎÓÊËÚ¸
‡
ji
=
r
a
ij
, Ú.Â. ÒÎÓÊËÚ¸
r
A Ò
r
A
t
: Ä =
r
A +
r
A
t
, „‰Â t – Á̇˜ÓÍ
Ú‡ÌÒÔÓÌËÓ‚‡ÌËfl χÚˈ˚. ➤
2.3. ëÇüáçéëíú, ñàäãõ à êÄáêÖáõ
ñÂÔ¸˛, ÒÓ‰ËÌfl˛˘ÂÈ ‚¯ËÌ˚ v Ë v′ ‚ „‡Ù G, ̇Á˚‚‡˛Ú
Ú‡ÍÛ˛ ÔÓÒΉӂ‡ÚÂθÌÓÒÚ¸ ÒÏÂÊÌ˚ı ·Â
rr r
ii i
1 25
, ,..., , ÍÓÚÓ-
‡fl ̇˜Ë̇ÂÚÒfl ‚ ‚¯ËÌ v Ë ÍÓ̘‡ÂÚÒfl ‚ ‚¯ËÌ v′. ñÂÔ¸
̇Á˚‚‡ÂÚÒfl ÔÓÒÚÓÈ (ËÎË ˝ ÎÂÏÂÌÚ‡ÌÓÈ), ÂÒÎË ‚ ÌÂÈ ÌÂÚ Ò‡ÏÓ-
ÔÂÂÒ˜ÂÌËÈ, Ú.Â. ÔÓ‚ÚÓfl˛˘ËıÒfl ‚¯ËÌ. èÓÒÚ‡fl ˆÂÔ¸, Û
ÍÓÚÓÓÈ Ì‡˜‡ÎÓ ÒÓ‚Ô‡‰‡ÂÚ Ò ÍÓ̈ÓÏ v = v′, ̇Á˚‚‡ÂÚÒfl ÔÓÒÚ˚Ï
ˆËÍÎÓÏ. é˜Â‚ˉÌÓ, ˜ÚÓ ‚ ÌÂÔÓÒÚÓÈ ˆÂÔË ˜‡ÒÚ¸, ̇˜Ë̇˛˘‡flÒfl
Ë ÍÓ̘‡˛˘‡flÒfl ‚ ‚¯ËÌÂ, „‰Â ˆÂÔ¸ Ò‡ÏÓÔÂÂÒÂ͇ÂÚÒfl, Ó·‡ÁÛ-
ÂÚ Ì ӷflÁ‡ÚÂθÌÓ ÔÓÒÚÓÈ ˆËÍÎ.
ë‚flÁÌÓÒÚ¸. Ñ‚Â ‚¯ËÌ˚, ÒÓ‰ËÌfl˛˘ËÂÒfl ‚ „‡ÙÂ Ô ÓÒÚÓÈ
ˆÂÔ¸˛, ̇Á˚‚‡˛Ú Ò‚flÁ‡ÌÌ˚ÏË (ËÎË ÒÓÓ·˘‡˛˘ËÏËÒfl, Ò‚flÁÌ˚-
ÏË). Ç ÌÂÓËÂÌÚËÓ‚‡ÌÌÓÏ „‡Ù ÔÓ ˆÂÔË ÏÓÊÌÓ ‰‚Ë„‡Ú¸Òfl ͇Í
ÓÚ v Í v′ Ú‡Í Ë ÓÚ v′ Í v. é·ÓÁ̇˜ËÏ ·Ë̇ÌÓ ÓÚÌÓ¯ÂÌËÂ
Ò‚flÁÌÓÒÚË Ì‡ ÌÂÓËÂÌÚËÓ‚‡ÌÌÓÏ „‡Ù ÒËÏ‚ÓÎÓÏ S. í‡Í ͇Í
vSv′ = v′Sv, ÚÓ S ÒËÏÏÂÚ˘ÌÓ.
ÖÒÎË vSv′, ‡ v′Su, ÚÓ ÒÛ˘ÂÒÚ‚ÛÂÚ ˆÂÔ¸ ËÁ vbu Ë ‚˚ÔÓÎÌflÂÚ-
Òfl ÓÚÌÓ¯ÂÌË vSu, Ú.Â. S Ú‡ÌÁËÚË‚ÌÓ. ÑÓÔÛÒ͇fl ˆÂÔË ‰ÎËÌ˚
0, ÔÓÎÛ˜‡ÂÏ ÂÙÎÂÍÒË‚ÌÓÒÚ¸ S:vSv.
í‡ÍËÏ Ó·‡ÁÓÏ, ÓÚÌÓ¯ÂÌË ҂flÁÌÓÒÚË ÂÙÎÂÍÒË‚ÌÓ, ÒËÏÏÂÚ-
˘ÌÓ Ë Ú‡ÌÁËÚË‚ÌÓ, Ú.Â. ÓÌÓ ÂÒÚ¸ ˝Í‚Ë‚‡ÎÂÌÚÌÓÒÚ¸ ̇ ÏÌÓÊÂ-
ÒÚ‚Â V. èÓ ÓÚÌÓ¯ÂÌ˲ S ÌÓÒËÚÂθ „‡Ù‡ V(G) ‡Á·Ë‚‡ÂÚÒfl ̇
ÌÂÔÂÂÒÂ͇˛˘ËÂÒfl Í·ÒÒ˚
75
V = V
1
∪V
2
∪...∪V
k
; V
i
∩V
j
= ∅; i, j = 1, 2,..., n.
ùÚÓ ‡Á·ËÂÌË ÌÓÒËÚÂÎfl „‡Ù‡ G ÔÓÓʉ‡ÂÚ ÒÓÓÚ‚ÂÚÒÚ‚Û˛˘ÂÂ
‡Á·ËÂÌË ҇ÏÓ„Ó „‡Ù‡ ̇ ˜‡ÒÚË G
1
, G
2
,..., G
k
, ̇Á˚‚‡ÂÏ˚Â
ÍÓÏÔÓÌÂÌÚ‡ÏË „‡Ù‡. åÂÊ‰Û ‚¯Ë̇ÏË ËÁ ‡ÁÌ˚ı ÍÓÏÔÓÌÂÌÚ
ÌÂÚ Â·Â, ‡ ÒÚ‡ÎÓ ·˚ Ú¸, Ë ˆÂÔÂÈ. äÓÏÔÓÌÂÌÚ˚ Ì ҂flÁ‡Ì˚ ‰Û„
Ò ‰Û„ÓÏ.
èË Î˛·ÓÏ ËÁÓÏÓ ÙËÁÏ ҂flÁ̇fl ÍÓÏÔÓÌÂÌÚ‡ ÒÓı‡ÌflÂÚ
Ò‚flÁÌÓÒÚ¸ Ë ˜ËÒÎÓ ‚¯ËÌ. á̇˜ËÚ, ˜ËÒ· ÍÓÏÔÓÌÂÌÚ ‚ ËÁÓ-
ÏÓÙÌ˚ı „‡Ù‡ı ÒÓ‚Ô‡‰‡˛Ú: χ = χ(G) = χ(G
∗
), ÂÒÎË G Y G
∗
.
äÓ΢ÂÒÚ‚Ó ÍÓÏÔÓÌÂÌÚ „‡Ù‡ χ ËÌ‚‡Ë‡ÌÚÌÓ ˜ËÒÎÛ „‡Ù‡ G:
Â„Ó Ì‡Á˚‚‡˛Ú Ò‚flÁÌÓÒÚ¸˛ „‡Ù‡. ɇÙ, Û ÍÓÚÓÓ„Ó Ó‰Ì‡ ÍÓÏÔÓ-
ÌÂÌÚ‡ Ò‚flÁÌÓÒÚË, ̇Á˚‚‡ÂÚÒfl Ò‚flÁÌ˚Ï. ɇÙ, Û ÍÓÚÓÓ„Ó ÓÚÒÛÚ-
ÒÚ‚Û˛Ú ˆËÍÎ˚, ̇Á˚‚‡˛Ú ‡ˆËÍ΢ÂÒÍËÏ. ñËÍÎ ËÁ n ‚¯ËÌ
ÏÓÊÂÚ ‡ÒÒχÚË‚‡Ú¸Òfl Í‡Í ˆÂÔ¸, ÍÓÚÓ‡fl ̇˜Ë̇ÂÚÒfl Ë ÍÓ̘‡-
ÂÚÒfl ‚ β·ÓÈ Â ‚¯ËÌÂ. ñËÍÎ ÔÓfl ‰Í‡ n Ó·ÓÁ̇˜‡ÂÚÒfl Ó·˚˜ÌÓ
ÒËÏ‚ÓÎÓÏ ë
n
. Ç ÌÂ„Ó ‚ıÓ‰flÚ ÚÓθÍÓ ‚¯ËÌ˚ ÒÚÂÔÂÌË ‰‚‡. ÖÒÎË
ëë
nn
1 2
Ë ËÏÂ˛Ú Ó·˘Â ·Ó, ÚÓ ÔË Ì‡ÎÓÊÂÌËË Ëı ‰Û„ ̇
‰Û„‡ ÔÓ ÏÓ‰Ûβ 2 (˜ÚÓ ‡‚ÌÓÒËθÌÓ Û‰‡ÎÂÌ˲ Ó·˘Â„Ó Â·‡)
ÔÓÎÛ˜‡ÂÚÒfl ˆËÍÎ
ë
nn
1 2
1+ −
. ÖÒÎË Û ‰‚Ûı ˆËÍÎÓ‚ Ó·˘ËÏË fl‚Îfl˛ÚÒfl
r ·Â, ÚÓ ÔË ÒÎÓÊÂÌËË Ëı ÔÓ ÏÓ‰Ûβ ‰‚‡ ÔÓÎÛ˜ËÚÒfl ˆËÍÎ
ÔÓfl‰Í‡ n
1
+ n
2
– r. çÂÁ‡‚ËÒËÏ˚ ˆËÍÎ˚ ÔË ÒÎÓÊÂÌËË ÔÓ ÏÓ-
‰Ûβ 2 ÒÓı‡Ìfl˛ÚÒfl. èÓ˝ÚÓÏÛ ÔÓËÁ‚ÓθÌ˚È Ì‡·Ó ˆËÍÎÓ‚
(Í‚‡ÁˈËÍÎ) ÔÂÂıÓ‰ËÚ ‚ ̇·Ó ˆËÍÎÓ‚ Ê (ÌÓ, ÏÓÊÂÚ ·˚Ú¸,
ÏÂ̸¯Â„Ó ˜ËÒ·).
äÓÏÔÓÌÂÌÚ˚ „‡Ù‡. ì͇ÊÂÏ ÏÂÚÓ‰ ÔÓÒÚÓÂÌËfl ÍÓÏÔÓÌÂÌÚ
„‡Ù‡. èÓ ÔÓËÁ‚ÓθÌÓÈ ‚¯ËÌ v „‡Ù‡ G ̇ȉÂÏ ÏÌÓÊÂÒÚ-
‚Ó Sv, ÒÓÒÚÓfl˘Â ËÁ ‚ÒÂı ‚¯ËÌ, ÒÏÂÊÌ˚ı Ò v. èÛÒÚ¸ ÓÌÓ
‚Íβ˜‡ÂÚ ‚¯ËÌ˚ v
1
, v
2
,..., v
s
(s
1
= s(v) – ÒÚÂÔÂ̸ ‚ ¯ËÌ˚
v). ÑÎfl ͇ʉÓÈ v
i
ÓÔ‰ÂÎflÂÏ ÏÌÓÊÂÒÚ‚Ó Â ÒÏÂÊÌËÍÓ‚ Ë ·Â-
ÂÏ Ëı Ó·˙‰ËÌÂÌËÂ
Sv Sv Sv S Sv S v
v1 2
1
2
∪∪ ==... ( ) .
Ç S
2
v ·Û‰ÛÚ ‚ı Ó‰ËÚ¸ ‚¯ËÌ˚ „ ‡Ù‡ G, ‚ ÍÓÚÓ˚ ÏÓÊÌÓ ÔÓ-
Ô‡ÒÚ¸ ÔÓ ˆÂÔflÏ ‰ÎËÌ˚ 2 ËÁ ‚¯ËÌ˚ v. Ä̇Îӄ˘ÌÓ ÓÔ‰ÂÎfl-
ÂÚÒfl S
2
v Í‡Í ÏÌÓÊÂÒÚ‚Ó ‚¯ËÌ, ‰ÓÒÚËÊËÏ˚ı ËÁ v ÔÓ ˆÂÔflÏ ËÁ
ÚÂı ·Â. ë‡ÏÓ v ‰ÓÒÚËÊËÏÓ ËÁ v ÔÓ ÔÛÚflÏ ‰ÎËÌ˚ ÌÛθ:
v = S
0
v.
é·‡ÁÛÂÏ ÔÓÒΉӂ‡ÚÂθÌ˚ ÒÛÏÏ˚
D
0
(v) = S
0
v,
D
1
(v) = S
0
v ∪Sv,
76
D
2
(v) = S
0
v ∪ Sv ∪ S
2
v,
........................................
D
p
(v) = D
p–1
(v) ∪ S
p
v =
Sv
k
k
p
.
= 0
U
D
p
(v) ‰‡ÂÚ ÏÌÓÊÂÒÚ‚Ó ‚¯ËÌ, ‰ÓÒÚËÊËÏ˚ı ËÁ v ÔÓ ˆÂÔflÏ
‰ÎËÌ˚ l ≤ p. è‰ÂθÌÛ˛ ‰ÎËÌÛ ˆÂÔË ÏÓÊÌÓ ÓÔ‰ÂÎËÚ¸ Ú‡Í:
ÂÒÚ¸ ÏËÌËχθÌ˚È Ë̉ÂÍÒ k, ÔË ÍÓÚÓÓÏ D
k+1
(v) = D
k
(v).
ùÚÓ ÓÁ̇˜‡ÂÚ, ˜ÚÓ ‰Îfl ÔÓÒÚÓÂÌËfl ÍÓÏÔÓÌÂÌÚ˚ G(v) „‡Ù‡ G,
ÒÓ‰Âʇ˘ÂÈ ‚¯ËÌÛ v, ‰ÓÒÚ‡ÚÓ˜ÌÓ ËÒÔÓθÁÓ‚‡Ú¸ ˆÂÔË ‰ÎËÌ˚
l ≤ p.
Ç „‡Ù G, ÒÓ‰Âʇ˘ÂÏ ˆËÍÎ˚, ÏÂÊ‰Û Ô‡‡ÏË ‚¯ËÌ ÒÛ-
˘ÂÒÚ‚Û˛Ú ˆÂÔË ÌÂÓ„‡Ì˘ÂÌÌÓÈ ‰ÎËÌ˚; ˝ÚÓ ·Û‰ÛÚ ˆÂÔË Ò Ò‡ÏÓ-
ÔÂÂÒ˜ÂÌËflÏË, ÚÓ ÂÒÚ¸ ˆËÍ·ÏË.
èÓÒÍÓθÍÛ D
k
(v) ⊂ D
k+1
ÔË k < p, ÚÓ
D
k+1
(v) > D
k
(v), ‡ D
p+1
= D
p
.
ÖÒÎË v ËÁÓÎËÓ‚‡Ì̇fl ÚӘ͇, ÚÓ p(v) = 1. Ç ÔÓÚË‚ÌÓÏ ÒÎÛ-
˜‡Â D
k
(v) > k, D
k+1
(v) > k + 1 ‚ÔÎÓÚ¸ ‰Ó k = p – 1. Ç
ÚӘ͠k = p(v) ÓÒÚ D
k
(v) ÓÒڇ̇‚ÎË‚‡ÂÚÒfl. éÚÒ˛‰‡ ‚ˉÌÓ, ˜ÚÓ
max
vV
Pv n
∈
≤() .
àÚ‡Í, Ï˚ ۷‰ËÎËÒ¸, ˜ÚÓ ÍÓÏÔÓÌÂÌÚÛ Ò‚fl ÁÌÓÒÚË G(v), ÒÓ-
‰Âʇ˘Û˛ ‚¯ËÌÛ v „‡Ù‡ G, ÏÓÊÌÓ ÒÚÓËÚ¸ Í‡Í ÏÌÓÊÂÒÚ‚Ó
vS S Sppv
vv v
p
∪∪∪∪ =
2
... ; ( ).
äÓ„‰‡ ÍÓÏÔÓÌÂÌÚ‡ Ì ËÒ˜ÂÔ˚‚‡ÂÚ ‚ÒÂ„Ó G, Ú.Â. ÏÌÓÊÂÒÚ‚Ó V′ =
= V – G(v) Ì ÔÛÒÚÓ, ÚÓ„‰‡ ̇ȉÂÚÒfl v′ ∈ V′, ‰Îfl ÍÓÚÓÓÈ Ì‡‰Ó
ÔÓ‚ÚÓËÚ¸ ÔÓˆÂÒÒ ÔÓÒÚÓÂÌËfl ÒÓ‰Âʇ˘ÂÈ Â ÍÓÏÔÓÌÂÌÚ˚
G(v′).
ÖÒÎË V″ = V′ – G(v′) ÌÂ ÔÛÒÚÓ, ÚÓ ·ÂÂÏ v″ ËÁ V″. çÓÏÂ
¯‡„‡ k = k(G), ̇ ÍÓÚÓÓÏ ÔÓˆÂÒÒ ÔÓÒÚÓÂÌËfl ÌÓ‚˚ı ÍÓÏÔÓ-
ÌÂÌÚ ËÒ˜ÂÔ‡ÂÚ ‚Ò ÚÓ˜ÍË V(G), Ë ·Û‰ÂÚ ˜ËÒÎÓÏ ÍÓÏÔÓÌÂÌÚ
„‡Ù‡ χ(G). üÒÌÓ, ˜ÚÓ Ô‰ÎÓÊÂÌÌ˚È ÏÂÚÓ‰ ÔflÏÓ„Ó ÔÓÒÚÓÂ-
ÌËfl ÍÓÏÔÓÌÂÌÚ „‡Ù‡ ÌÂθÁfl ‡ÒÔÓÒÚ‡ÌflÚ¸ ̇ „‡Ù˚ ÒÓ
Ò˜ÂÚÌ˚Ï ÏÌÓÊÂÒÚ‚ÓÏ ‚¯ËÌ.
ã„ÍÓ Û·Â‰ËÚ¸Òfl ‚ ÚÓÏ, ˜ÚÓ ‰Îfl ÍÓ̘ÌÓ„Ó „‡Ù‡ G Ò χ ÍÓÏ-
ÔÓÌÂÌÚ‡ÏË, χÚËˆÛ Ä(G) ÏÓÊÌÓ ÔË‚ÂÒÚË Í ·ÎÓ˜ÌÓ-
‰Ë‡„Ó̇θÌÓÏÛ ‚ˉÛ. ÑÎfl ˝ÚÓ„Ó ÔÂÂÒÚ‡ÌÓ‚ÍÓÈ fl‰Ó‚ (ÒÚÓÍ Ë
ÒÚÓηˆÓ‚) ̇‰Ó ÓÚÓ·‡Ú¸ Ò̇˜‡Î‡ ‚¯ËÌ˚ Ó‰ÌÓÈ ÍÓÏÔÓÌÂÌÚ˚,
Ò͇ÊÂÏ G
1
, Ë ÔËÒ‚ÓËÚ¸ ËÏ Ë̉ÂÍÒ˚ ÓÚ 1 ‰Ó n
1
= n(G). á‡ÚÂÏ

77
‚¯ËÌ‡Ï ‰Û„ÓÈ ÍÓÏÔÓÌÂÌÚ˚ G
2
ÔËÒ‚ÓËÚ¸ Ë̉ÂÍÒ˚ ÓÚ n
1
+ 1
‰Ó n
1
+ n
2
Ë Ú.‰. íÓ„‰‡ Ä(G) ÔËÏÂÚ ‚ˉ
A
A
A
A
(
()
()
()
G) =
G
G
G
1
2
00
0
0
M
LL
M
∴
χ
.
í‡ÍÓÈ ‚ˉ ÏÓÊÌÓ Ôˉ‡Ú¸ χÚˈ A(G), ÂÒÎË Ó̇ ÔË‚Ó-
‰Ëχ. ëÛ˘ÂÒÚ‚Û˛Ú ‡Î„·‡Ë˜ÂÒÍË ÏÂÚÓ‰˚ ÔÓËÒ͇ ÌÂÔË‚Ó‰Ë-
Ï˚ı ÍÓÏÔÓÌÂÌÚ Ï‡Úˈ, ÌÓ ˝ÚÓ ÛÊ ÓÚÌÓÒËÚÒfl Í ‡Î„·Â, ‡ Ì Í
ÚÂÓËË „‡ÙÓ‚. ɇ٠G
1
̇ ËÒ. 2 ÒÎÛÊËÚ ÔËÏÂÓÏ ÚÂı ÍÓÏ-
ÔÓÌÂÌÚÌÓ„Ó „‡Ù‡.
Ñ‚¸fl Ë ÓÒÚÓ‚˚ „‡ÙÓ‚. LJÊÌ˚È Í·ÒÒ Ò‚flÁÌ˚ı „‡ÙÓ‚
Ô‰ÒÚ‡‚Îfl˛Ú Ú‡Í Ì‡Á˚‚‡ÂÏ˚ ‰Â‚¸fl. ì ‰Â‚‡ ÒÛ˘ ÂÒÚ‚ÛÂÚ
ÏÌÓ„Ó ‡‚ÌÓÒËθÌ˚ı ÓÔ‰ÂÎÂÌËÈ. å˚ ÓÔ‰ÂÎËÏ ‰ÂÂ‚Ó Í‡Í
Ò‚flÁÌ˚È „‡Ù ·ÂÁ ˆËÍÎÓ‚. éÚÏÂÚËÏ ‚‡ÊÌ˚Â Ò ‚ Ó È Ò Ú ‚ ‡ ‰   -
‚ ¸ Â ‚ .
1. ì ‰Â Â‚‡ ÂÒÚ¸ ‰ËÌÒÚ‚ÂÌ̇fl ˆÂÔ¸, ÒÓ‰ËÌfl˛˘‡fl ‰‚ Á‡-
‰‡ÌÌ˚ ‚¯ËÌ˚ v Ë v′. ÖÒÎË ·˚ ËÏÂÎÓÒ¸ ‰‚ ˆÂÔË ÏÂÊ‰Û v Ë
v′, ÚÓ Ò ÏÓÏÂÌÚ‡ Ëı ‡Á˙‰ËÌÂÌËfl ‚ ÚӘ͠v″ ‰‚ ‡ÁÌ˚ ˆÂ-
ÔÓ˜ÍË ÓÚ v″ Í v′ ‰‡ÎË ·˚ ˆËÍÎ. á̇˜ËÚ, ÚÓ˜ÍË ‡Á˙‰ËÌÂÌËfl
‰‚Ûı ˆÂÔÂÈ v″ Ì ÒÛ˘ÂÒÚ‚ÛÂÚ.
2. ÑÂÂ‚Ó í ÔÓfl‰Í‡ n ËÏÂÂÚ m(T) = n – 1 · . ÖÒÎË
m(T) < n – 1, ÚÓ ‚Ò„‰‡ ̇ȉÂÚÒfl ËÁÓÎËÓ‚‡Ì̇fl ‚¯Ë̇, ˜ÚÓ
Ô ÓÚË‚Ó˜ËÚ Ò‚flÁÌÓÒÚË ‰Â‚‡. ÖÒÎË m(T) ≥ n, ÚÓ ‰ÓÎÊÂÌ
·˚Ú¸ ıÓÚfl ·˚ Ó‰ËÌ ˆËÍÎ Ò ‰‚ÛÏfl ‚¯Ë̇ÏË. ÇÂÌÓ Ë Ó·‡Ú-
ÌÓ – Ò‚flÁÌ˚È „‡Ù ÚËÔ‡ (n, n – 1) ‚Ò„‰‡ fl‚ÎflÂÚÒfl ‰Â‚ÓÏ.
3. óËÒÎÓ ‚ËÒfl˜Ëı ‚¯ËÌ ‚ ‰Â‚ ˜ÂÚÌÓ Ë Ì ÏÂÌ ‰‚Ûı.
èÛÒÚ¸ G – ÔÓÒÚÓÈ Ò‚flÁÌ˚È „‡Ù. ÑÂÂ‚Ó í
G
ÔÓfl‰Í‡ n =
= n(G), ÒÓ‰ËÌfl˛˘Â ‚Ò ‚¯ËÌ˚ „‡Ù‡ G, ̇Á˚ ‚‡ÂÚÒfl ÒÚfl-
„Ë‚‡˛˘ËÏ ‰Â‚ÓÏ „‡Ù‡, Â„Ó ÓÒÚÓ‚ÓÏ ËÎË Í‡Í‡ÒÓÏ. ì „‡Ù‡
G ÏÓÊÂÚ ·˚Ú¸ ÌÂÒÍÓθÍÓ ÓÒÚÓ‚Ó‚, ÂÒÎË G Ì ‰Â‚Ó. ä‡Í‡ÒÓÏ
‰Â‚‡ fl‚ÎflÂÚÒfl ÚÓθÍÓ ÓÌÓ Ò‡ÏÓ.
ǂ‰ÂÏ Â˘Â Ó‰ÌÓ ˜ËÒÎÓ „‡Ù‡, ÍÓÚÓÓ ̇Á˚‚‡˛Ú ˆËÍÎÓχ-
Ú˘ÂÒÍËÏ. èÓ ÓÔ‰ÂÎÂÌ˲ ÓÌÓ Á‡‰‡ÂÚÒfl ÙÓÏÛÎÓÈ
ν = ν(G) = m(G) – n(G) + χ(G);
ν – fl‚ÎflÂÚÒfl ˜ËÒÎÓÏ „‡Ù‡, Ú‡Í Í‡Í ‚˚ ‡Ê‡ÂÚÒfl ˜ÂÂÁ ˜ËÒ·
„‡Ù‡ m, n, χ.
ñËÍÎÓχÚ˘ÂÒÍÓ ˜ËÒÎÓ, Í‡Í ·Û‰ÂÚ ‚ˉÌÓ ‰‡ÎÂÂ, Ò‚flÁ‡ÌÓ Ò
ÍÓ΢ÂÒÚ‚ÓÏ ÌÂÁ‡‚ËÒËÏ˚ı ˆËÍÎÓ‚ ‚ „‡ÙÂ. ùÚË ˆËÍÎ˚ ÒÚÓflÚ Ò
ÔÓÏÓ˘¸˛ ÓÒÚÓ‚Ó‚.
í Â Ó Â Ï ‡ 6. ñËÍÎÓχÚ˘ÂÒÍÓ ˜ËÒÎÓ ‰Â‚‡ Ë Î˛·Ó„Ó ‰Û-
„Ó„Ó ‡ˆËÍ΢ÂÒÍÓ„Ó „‡Ù‡ ‡‚ÌÓ ÌÛβ.
