Овчаров Л.А. и др. Математические модели информационых процессов и управления
Подождите немного. Документ загружается.


48
ã˛·ÓÈ „‡Ù ÔÓfl‰Í‡ n ‡ÒÔÓ·„‡ÂÚÒfl „‰Â-ÚÓ ÏÂÊ‰Û „Û‰ÓÈ
N
n
Ë ÍÎËÍÓÈ K
n
‚ ÚÓÏ ÒÏ˚ÒÎÂ, ˜ÚÓ ‰Îfl Ëı Ò˄̇ÚÛ ‚˚ÔÓÎÌfl˛Ú-
Òfl ‚Íβ˜ÂÌËfl R(N
n
) ⊆ R(G) ⊆ R(K
n
).
燉 „‡Ù‡ÏË (Í‡Í ÏÌÓÊÂÒÚ‚‡ÏË) ÓÔ Â‰ÂÎÂÌ˚ ·Ë̇Ì˚ ÓÔÂ-
‡ˆËË: Ó·˙‰ËÌÂÌËÂ, Ó·ÓÁ̇˜‡ÂÏÓ Á̇ÍÓÏ ∪ Ë ÔÂÂÒ˜ÂÌË –
ÁÌ‡Í ∩. é·˙‰ËÌÂÌË ç
1
∪ç
2
Ë ÔÂÂÒ˜ÂÌË ç
1
∪ç
2
ÓÔ‰ÂÎfl-
˛ÚÒfl ÚÂÓÂÚËÍÓ-ÏÌÓÊÂÒÚ‚ÂÌÌÓ:
V(H∪H
2
) = V(H
1
)∪V(H
2
); R(H
1
∪H
2
) = R(H
1
)∪R(H
2
);
V(H
1
∩H
2
) = V(H
1
)∩V(H
2
); R(H
1
∩H
2
) = R(H
1
)∩R(H
2
).
ÖÒÎË H
1
Ë H
2
Ì ÔÂÂÒÂ͇˛ÚÒfl ÔÓ ‚¯ËÌÂ, ÚÓ Ëı Ó·˙‰ËÌÂ-
ÌË ̇Á˚‚‡˛Ú ÔflÏÓÈ ÒÛÏÏÓÈ „‡ÙÓ‚ Ë Ó·ÓÁ̇˜‡˛Ú H
1
+ H
2
.
ÖÒÎË H
1
Ë H
2
– ‰‚ ˜‡ÒÚË „‡Ù‡ G, ÚÓ Ëı ‡ÁÌÓÒÚ¸˛ H
1
–
– H
2
·Û‰ÂÏ Ò˜ËÚ‡Ú¸ „‡Ù Ò ÌÓÒËÚÂÎÂÏ
VV
1 2
∩ Ë Ò˄̇ÚÛÓÈ
RR
1 2
∩ . éÌ ‚Íβ˜‡ÂÚ ‚ ¯ËÌ˚ ç
1
, Ì ‚ıÓ‰fl˘Ë ‚ ç
2
, Ë Â·‡
R
1
Ë fl‚ÎflÂÚÒfl ÔÓ‰„‡ÙÓÏ G, ÔÓÓʉÂÌÌ˚Ï ‚¯Ë̇ÏË V
1
∩
V
2
.
é·˚˜ÌÓ ‚ ͇˜ÂÒÚ‚Â ÔËÏ ӂ „ ‡ÙÓ‚ “ËÁ ÊËÁÌË” ÔË‚Ó‰flÚ
ÒËÒÚÂÏ˚ ÍÓÏÏÛÌË͇ˆËÈ, ˝ÎÂÍÚ˘ÂÒÍË ÒÂÚË, ÏÌÓ„ÓÌËÚÓ˜Ì˚Â
„‡ÁÓ- Ë ÌÂÙÚÂÔÓ‚Ó‰˚, ÒÚÛÍÚÛ˚ Ó„‡ÌËÁ‡ˆËË Û˜ÂʉÂÌËÈ Ò
ÓÚÌÓ¯ÂÌËÂÏ ÔÓ‰˜ËÌÂÌÌÓÒÚË Ó„‡ÌÓ‚ Ë Ú.Ô.
ì Ô ‡ Ê Ì Â Ì Ë Â. ç‡ËÒÛÈÚ ÒÚÛÍÚÛÛ Ç‡¯Â„Ó ‚ÛÁ‡.
ä·ÒÒËÙË͇ˆËfl
‚¯ËÌ,
ÔÓ‰„‡ÙÓ‚ Ë „‡ÙÓ‚; Ò‚fl Á‡ÌÌÓÒÚ¸.
ê‡ÒÒÏÓÚËÏ ÓËÂÌÚËÓ‚‡ÌÌ˚È „‡Ù
r
G( R),V, Ëϲ˘ËÈ n ‚Â-
¯ËÌ. ǯË̇ v
i
ÓËÂÌÚËÓ‚‡ÌÌÓ„Ó „‡Ù‡
r
G ̇Á˚‚‡ÂÚÒfl ËÁÓ-
ÎËÓ‚‡ÌÌÓÈ, ÂÒÎË ÌÂÚ ÌË Ó‰ÌÓ„Ó Â·‡, ÒÓ‰ËÌfl˛˘Â„Ó ‚¯ËÌ˚
v
i
Ë v
i
(j =
1, n, i ≠ j). èË ˝ÚÓÏ ‚ÓÁÏÓÊÂÌ ÒÎÛ˜‡È, ÍÓ„‰‡ n = ∞.
àÁÓÎËÓ‚‡Ì̇fl ‚¯Ë̇ v
i
ËÁÓ·‡ÊÂ̇ ̇ ËÒ. 2.19. ì ËÁÓÎË-
Ó‚‡ÌÌÓÈ ‚¯ËÌ˚ ÌÂÚ ÌË Ó‰ÌÓÈ ÒÓÒ‰ÌÂÈ ‚¯ËÌ˚ Ë Ó̇ ÌÂ
fl‚ÎflÂÚÒfl ÒÓÒ‰ÌÂÈ ÔÓ ÓÚÌÓ¯ÂÌ˲ Í Î˛·ÓÈ ‰Û„ÓÈ ‚¯ËÌÂ
„‡Ù‡.
ǯË̇ v
i
̇Á˚‚‡ÂÚÒfl ̇˜‡Î¸ÌÓÈ (ËÒÚÓ˜ÌËÍÓÏ), ÂÒÎË Û
˝ÚÓÈ ‚¯ËÌ˚ ÂÒÚ¸ ıÓÚfl ·˚ Ӊ̇ ÒÓÒ‰Ìflfl ‚¯Ë̇, ÌÓ Ó̇ ÌÂ
fl‚ÎflÂÚÒfl ÒÓÒ‰ÌÂÈ ÔÓ ÓÚÌÓ¯ÂÌ˲ Í ‰Û„ËÏ ‚¯Ë̇Ï.
ç‡ ËÒ. 2.20 ‚¯Ë̇ v
i
fl‚ÎflÂÚÒfl ̇˜‡Î¸ÌÓÈ.
ǯË̇ v
i
̇Á˚‚‡ÂÚÒfl ÍÓ̈‚ÓÈ (ÔÓ„ÎÓ˘‡˛˘ÂÈ), ÂÒÎË Ó̇
fl‚ÎflÂÚÒfl ÒÓÒ‰ÌÂÈ ÔÓ ÓÚÌÓ¯ÂÌ˲ ıÓÚfl ·˚ Í Ó‰ÌÓÈ ‚¯ËÌÂ
„‡Ù‡, ÌÓ Û Ì ÌÂÚ ÌË Ó‰ÌÓÈ ÒÓÒ‰ÌÂÈ ‚¯ËÌ˚ „‡Ù‡.
ç‡ ËÒ. 2.20 ÍÓ̈‚ÓÈ fl‚ÎflÂÚÒfl ‚¯Ë̇ v
4
.
ǯË̇ v
i
̇Á˚‚‡ÂÚÒfl Ú‡ÌÁËÚË‚ÌÓÈ, ÂÒÎË Ó̇ fl ‚ÎflÂÚÒfl
ÒÓÒ‰ÌÂÈ ÔÓ ÓÚÌÓ¯ÂÌ˲ ıÓÚfl ·˚ Í Ó‰ÌÓÈ ‚¯ËÌ „‡Ù‡ Ë Û
˝ÚÓÈ ‚¯ËÌ˚ ÂÒÚ¸ ı ÓÚfl ·˚ Ӊ̇ ÒÓÒ‰Ìflfl ‚¯Ë̇ „‡Ù‡. ç‡
ËÒ. 2.20 ‚¯ËÌ˚ v
2
, v
3
, v
5
– Ú‡ÌÁËÚË‚Ì˚Â.

49
ÖÒÎË ËÁÓÎËÓ‚‡Ì̇fl ‚¯Ë̇ v
i
ËÏÂÂÚ ÔÂÚβ, ÚÓ Ó̇ ËÏÂÂÚ
„‡Ù, ÔÓ͇Á‡ÌÌ˚È Ì‡ ËÒ. 2.21. èÂÚÎË ÏÓ„ÛÚ ËÏÂÚ¸ ̇˜‡Î¸Ì˚Â,
ÍÓ̈‚˚Â Ë Ú‡ÌÁËÚË‚Ì˚ ‚¯ËÌ˚ ( ËÒ. 2.22).
ó‡˘Â ‚ÒÂ„Ó ÓËÂÌÚËÓ‚‡ÌÌ˚ „‡Ù˚ (Ò ÔÂÚÎflÏË ËÎË ·ÂÁ ÔÂ-
ÚÂθ) ·Û‰ÂÏ ËÒÔÓθÁÓ‚‡Ú¸ ‰Îfl ÚÓ„Ó, ˜ÚÓ·˚ ÒÚÓËÚ¸ χÚÂχÚ˘Â-
ÒÍË ÏÓ‰ÂÎË ËÌÙÓχˆËÓÌÌ˚ı ÔÓˆÂÒÒÓ‚ Ë ÛÔ‡‚ÎÂÌËfl, ‚ ÍÓ-
ÚÓ˚ı ÒËÒÚÂχ ÏÂÌflÂÚ Ò‚ÓË ÒÓÒÚÓflÌËfl.
è Ë Ï Â 7. ɇÙ, ËÁÓ·‡ÊÂÌÌ˚È Ì‡ ËÒ. 2.22, ÏÓÊÌÓ
Ú‡ÍÚÓ‚‡Ú¸ ÒÎÂ‰Û˛˘ËÏ Ó·‡ÁÓÏ. ëËÒÚÂχ (̇ÔËÏÂ, ùÇå) ‚
̇˜‡Î¸Ì˚È ÏÓÏÂÌÚ Ì‡ıӉ˷Ҹ ‚ ̇˜‡Î¸ÌÓÏ ÒÓÒÚÓflÌËË v
1
, „‰Â
Ó̇ ÏÓÊÂÚ ÔÓ·˚Ú¸ ͇ÍÓÂ-ÚÓ ‚ÂÏfl (‚ ÒËÎÛ Ì‡Î˘Ëfl ÔÂÚÎË) ËÎË
ÔÂÂÈÚË ‚ Ó‰ÌÓ ËÁ ÚÂı Ú‡ÌÁËÚË‚Ì˚ı (ÔÂÂıÓ‰Ì˚ı) ÒÓÒÚÓfl-
ÌËÈ: v
2
, v
3
, v
4
. ëÓÒÚÓflÌË v
1
‰Îfl ùÇå ÏÓÊÌÓ ‡ÒÒχÚË‚‡Ú¸
Í‡Í ÔÓ‰„ÓÚÓ‚ÍÛ ÌÓ‚ÓÈ ùÇå Í ˝ÍÒÔÎÛ‡Ú‡ˆËË (‡ÒÍÓÌÒ‚Ë-
Ó‚‡ÌËÂ, ÓÚ·‰Í‡, ÓÔÓ·Ó‚‡ÌËÂ).
èÓÔ‡‚ ‚ Ú‡ÌÁËÚË‚ÌÓ ÒÓÒÚÓflÌË v
2
, Ó̇ ÏÓÊÂÚ ÔÂÂÈÚË ÎË-
·Ó ‚ ÒÓÒÚÓflÌË v
5
, ÎË·Ó ‚ ÒÓÒÚÓflÌË v
4
. ÖÒÎË ÒËÒÚÂχ ÔÓÔ‡‰‡ÂÚ
‚ ÒÓÒÚÓflÌË v
4
, ÚÓ Ó̇ Ú‡Ï Ë ÓÒÚ‡ÌÂÚÒfl, Ú‡Í Í‡Í ÒÓÒÚÓflÌË v
4
fl‚ÎflÂÚÒfl ÍÓ̈‚˚Ï (ÔÓ„ÎÓ˘‡˛˘ËÏ). í‡ÍËÏ ÒÓÒÚÓflÌËÂÏ ‰Îfl
ùÇå ÏÓÊÂÚ ·˚Ú¸  ÒÔËÒ‡ÌË ‚ ÒËÎÛ ‚˚ıÓ‰‡  ËÁ ÒÚÓfl. ëÓ-
êàë. 2.19 êàë. 2.20
êàë. 2.21 êàë. 2.22
50
ÒÚÓflÌË v
2
ÏÓÊÌÓ ‡ÒÒχÚË‚‡Ú¸ Í‡Í ÒÓÒÚÓflÌËÂ, ÍÓ„‰‡ ùÇå
̇ıÓ‰ËÚÒfl ‚ ÂÏÓÌÚÂ.
èÓÔ‡‚ ‚ Ú‡ÌÁËÚË‚ÌÓ ÒÓÒÚÓflÌË v
3
, ùÇå ÔÂÂȉÂÚ ‚ ÒÓÒÚÓ-
flÌË v
4
, ËÁ ÍÓÚÓÓ„Ó Ó̇ ÛÊ Ì ‚˚ȉÂÚ. ëÓÒÚÓflÌË v
3
ÏÓÊÌÓ
‡ÒÒχÚË‚‡Ú¸ Í‡Í ÌÂÔ‡‚ËθÌÛ˛ ˝ÍÒÔÎÛ‡Ú‡ˆË˛ ùÇå, ÔÓÒÎÂ
˜Â„Ó Ó̇ ÔËıÓ‰ËÚ ‚ ÔÓÎÌÛ˛ Ì„ӉÌÓÒÚ¸ Ë ÒÔËÒ˚‚‡ÂÚÒfl.
ëÓÒÚÓflÌË v
5
ÏÓÊÌÓ Ô‰ÒÚ‡‚ÎflÚ¸ Í‡Í ÒÓÒÚÓflÌË ÌÓχθÌÓÈ
˝ÍÒÔÎÛ‡Ú‡ˆËË ùÇå. àÁ ˝ÚÓ„Ó ÒÓÒÚÓflÌËfl ùÇå ÏÓÊÂÚ Ô ÂÈÚË ‚
ÒÓÒÚÓflÌË v
2
(ÂÏÓÌÚËÛÂÚÒfl) Ë ËÁ ÒÓÒÚÓflÌËfl v
2
‚ÂÌÛÚ¸Òfl ‚
ÒÓÒÚÓflÌË v
5
(˝ÍÒÔÎÛ‡ÚËÛÂÚÒfl). ➤
ÑÓ ÒËı ÔÓ Ï˚ ‡ÒÒχÚË‚‡ÎË ÓÚ‰ÂθÌ˚ ÒÓÒÚÓflÌËfl . èÂÂÈ-
‰ÂÏ Í Í·ÒÒËÙË͇ˆËË ÔÓ‰ÏÌÓÊÂÒÚ‚ ÒÓÒÚÓflÌËÈ. ÑÎfl ̇„Îfl‰ÌÓÒ-
ÚË ·Û‰ÂÏ Ô‰ÔÓ·„‡Ú¸, ˜ÚÓ „‡Ù
r
G(V)
fl‚ÎflÂÚÒfl ÏÓ‰Âθ˛ ÌÂÍÓ-
ÚÓÓÈ ÒËÒÚÂÏ˚ S, ÍÓÚÓ‡fl ‚ÂÏfl ÓÚ ‚ÂÏÂÌË ÔÂÂıÓ‰ËÚ ËÁ Ó‰-
ÌÓ„Ó ÒÓÒÚÓflÌËfl (‚¯ËÌ˚) ‚ ‰Û„Ó ÒÓÒÚÓfl ÌË (‚¯ËÌÛ) ÔÓ
̇ԇ‚ÎÂÌ˲ ÓËÂÌÚËÓ‚‡ÌÌ˚ı ·Â.
凯ÛÚÓÏ ÔË ·ÎÛʉ‡ÌËË ÒËÒÚÂÏ˚ S ÔÓ ‚¯ËÌ‡Ï „‡Ù‡
r
G(V) ̇Á˚‚‡ÂÚÒfl ڇ͇fl ÔÓÒΉӂ‡ÚÂθÌÓÒÚ¸ ÓËÂÌÚËÓ‚‡ÌÌ˚ı
·Â, ÍÓ„‰‡ ‰‚‡ ÒÓÒ‰ÌËı ·‡ ËÏÂ˛Ú Ó‰ÌÛ Ó·˘Û˛
(ÔÓÏÂÊÛÚÓ˜ÌÛ˛) ‚¯ËÌÛ v
i
, ÔË ˝ÚÓÏ ‰Îfl Ó‰ÌÓ„Ó Â·‡
ÒÚÂÎ͇ ̇ԇ‚ÎÂ̇ Í ‚¯ËÌ v
i
, ‡ ‰Îfl ‰Û„Ó„Ó Â·‡ ÒÚ ÂÎ͇
̇ԇ‚ÎÂ̇ ËÁ ‚¯ËÌ˚ v
i
.
凯ÛÚ, ‚˚ıÓ‰fl˘ËÈ ËÁ ‚¯ËÌ˚ v
1
, ÔÓıÓ‰fl˘ËÈ ˜ÂÂÁ
‚¯ËÌ˚ v
2
, v
3
,..., v
k
Ë Á‡Í‡Ì˜Ë‚‡˛˘ËÈÒfl ‚ ‚¯ËÌ v
l
, ·Û‰ÂÏ
Ó·ÓÁ̇˜‡Ú¸ Í‡Í M(v
1
, v
2
, v
3
,..., v
k
,... v
l
). èË ˝ÚÓÏ ‚¯Ë̇ v
1
–
̇˜‡ÎÓ Ï‡¯ÛÚ‡, ‚ ¯Ë̇ v
l
– ÍÓ̈ χ¯ÛÚ‡, ‚¯Ë̇ v
k
–
ÔÓÏÂÊÛÚӘ̇fl ‚¯Ë̇ χ¯ÛÚ‡.
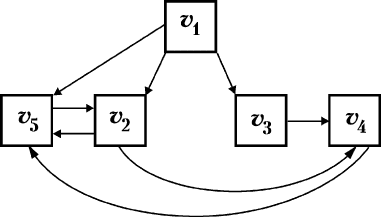
è Ë Ï Â 8. ì͇Á‡Ú¸ ˜ÂÚ˚ ‡Á΢Ì˚ı χ¯ÛÚ‡ ÏÂʉÛ
‚¯Ë̇ÏË v
1
Ë v
4
‰Îfl „‡Ù‡, ËÁÓ·‡ÊÂÌÌÓ„Ó Ì‡ ËÒ. 2.20.
ê Â ¯ Â Ì Ë Â.
1. M(v
1
, v
3
, v
4
),
2. M(v
1
, v
2
, v
4
),
3. M(v
1
, v
2
, v
5
, v
2
, v
4
),
4. M(v
1
, v
5
, v
2
, v
5
, v
2
, v
4
).
é·‡ÚËÚ ‚ÌËχÌË ̇ ÚÓ, ˜ÚÓ ‚ ÚÂÚ¸ÂÏ Ï‡¯ÛÚ ‚¯Ë̇
v
2
‚ÒÚ˜‡ÂÚÒfl ‰‚‡Ê‰˚, ‡ ‚ ˜ÂÚ‚ÂÚÓÏ Ï‡¯ÛÚ ‰‚‡Ê‰˚ ‚ÒÚÂ-
˜‡˛ÚÒfl ‚¯ËÌ˚ v
2
Ë v
5
. ➤
凯ÛÚ Ì‡Á˚‚‡ÂÚÒfl Ó‰ÌÓÒÚÓÓÌÌÂ-·ÂÒÍÓ̘Ì˚Ï, ÂÒÎË Û
ÌÂ„Ó ÂÒÚ¸ ̇˜‡Î¸Ì‡fl ‚¯Ë̇ Ë ÌÂÚ ÍÓ̘ÌÓÈ ‚¯ËÌ˚
(l
→ ∞).
í‡ÍË χ¯ÛÚ˚ Ì‡Ï ‚ÒÚÂÚflÚÒfl ÔË ËÁÛ˜ÂÌËË ÔÓˆÂÒÒÓ‚ „Ë-
·ÂÎË Ë ‡ÁÏÌÓÊÂÌËfl.
凯ÛÚ ÏÂÊ‰Û ‚¯Ë̇ÏË v
j
,..., v
l
̇Á˚‚‡ÂÚÒfl ÔÛÚÂÏ, ÂÒ-
ÎË Í‡Ê‰Ó ÓËÂÌÚËÓ‚‡ÌÌÓÂ Â·Ó ‚ ÌÂÏ ÔËÒÛÚÒÚ‚ÛÂÚ Ó‰ËÌ
51
‡Á (‚¯ËÌ˚ ‚ ÔÛÚË ÏÓ„ÛÚ Ë ÔÓ‚ÚÓflÚ¸Òfl). è‚˚ ÚË Ï‡¯-
ÛÚ‡, Ô˂‰ÂÌÌ˚ ‚ ÔËÏ 8, fl‚Îfl˛ÚÒfl ÔÛÚflÏË.
ÖÒÎË Ì‡˜‡ÎÓ Ï‡¯ÛÚ‡ ÒÓ‚Ô‡‰‡ÂÚ Ò Â„Ó ÍÓ̈ÓÏ (v
j
= v
l
), ÚÓ
Ú‡ÍÓÈ Ï‡¯ÛÚ Ì‡Á˚‚‡ÂÚÒfl ˆËÍ΢ÂÒÍËÏ.
ñËÍ΢ÂÒÍËÈ Ï‡¯ÛÚ Ì‡Á˚‚‡ÂÚÒfl ÍÓÌÚÛÓÏ, ÂÒÎË Í‡Ê‰ÓÂ
ÓËÂÌÚËÓ‚‡ÌÌÓÂ Â·Ó ‚ ÌÂÏ ÔËÒÛÚÒÚ‚ÛÂÚ Ó‰ËÌ ‡Á (‚¯Ë-
Ì˚ ‚ ÍÓÌÚÛÂ ÏÓ„ÛÚ ÔÓ‚ÚÓflÚ¸Òfl).
è Ë Ï Â 9. ç‡ ËÒ. 2.23 ËÁÓ·‡ÊÂÌ „‡Ù ‚ÓÁÏÓÊÌ˚ı ÒÓ-
ÒÚÓflÌËÈ ùÇå:
v
1
– ùÇå ÔÓıÓ‰ËÚ ‡ÒÍÓÌÒ‚‡ˆË˛, ÓÚ·‰ÍÛ Ë ÓÔÓ·Ó‚‡-
ÌËÂ,
v
2
– ùÇå ̇ıÓ‰ËÚÒfl ‚ ÂÏÓÌÚÂ,
v
3
– ùÇå ˝ÍÒÔÎÛ‡ÚËÛÂÚÒfl Ò „Û·˚ÏË Ì‡Û¯ÂÌËflÏË,
v
4
– ùÇå ÔÓıÓ‰ËÚ Í‡ÔËڇθÌ˚È ÂÏÓÌÚ,
v
5
– ùÇå ÌÓχθÌÓ ˝ÍÒÔÎÛ‡ÚËÛÂÚÒfl.
è˂‰ËÚ ÔËÏÂ˚ ˆËÍ΢ÂÒÍÓ„Ó Ï‡¯ÛÚ‡ Ë Ï‡¯ÛÚ‡,
ÍÓÚÓ˚È fl‚ÎflÂÚÒfl ÍÓÌÚÛÓÏ ‰Îfl „‡Ù‡, ËÁÓ·‡ÊÂÌÌÓ„Ó Ì‡ ËÒ.
2.23.
ê  ¯ Â Ì Ë Â. 凯ÛÚ M(v
2
, v
5
, v
2
, v
4
, v
5
) ˆËÍ΢ÂÒÍËÈ
(̇˜‡ÎÓ Ï‡¯ÛÚ‡ ÒÓ‚Ô‡‰‡ÂÚ Ò Â„Ó ÍÓ̈ÓÏ), ÌÓ ÓÌ Ì fl‚ÎflÂÚÒfl
ÍÓÌÚÛÓÏ, Ú‡Í Í‡Í Â·‡
r
z
(v
5
, v
2
) ‚ÒÚ˜‡ÂÚÒfl ‚ ÌÂÏ ‰‚‡Ê‰˚.
凯ÛÚ M(v
2
, v
4
, v
5
, v
2
) fl‚ÎflÂÚÒfl ÍÓÌÚÛÓÏ, Ú‡Í Í‡Í Ì‡˜‡ÎÓ
χ¯ÛÚ‡ ÒÓ‚Ô‡‰‡ÂÚ Ò Â„Ó ÍÓ̈ÓÏ Ë Í‡Ê‰ÓÂ Â·Ó ‚ÒÚ˜‡ÂÚÒfl ‚
˝ÚÓÏ Ï‡¯ÛÚ ӉËÌ ‡Á. ➤
é·ÓÁ̇˜ËÏ ÔÛÚ¸, ̇˜Ë̇˛˘ËÈÒfl ‚ ‚¯ËÌ v
j
, ÔÓıÓ‰fl˘ËÈ
˜ÂÂÁ ‚¯ËÌÛ v
k
Ë Á‡Í‡Ì˜Ë‚‡˛˘ËÈÒfl ‚ ‚¯ËÌ v
j
, ÒÎÂ‰Û˛-
˘ËÏ Ó·‡ÁÓÏ: è(v
j
,..., v
k
,..., v
l
). åÓÊÌÓ ‰Ó͇Á‡Ú¸, ˜ÚÓ ÂÒÎË ÒÛ-
˘ÂÒÚ‚ÛÂÚ Ï‡¯ÛÚ ÏÂÊ‰Û ‚¯Ë̇ÏË v
j
Ë v
l
, ÚÓ ÒÛ˘ÂÒÚ‚ÛÂÚ Ë
ÔÛÚ¸ ÏÂÊ‰Û ˝ÚËÏË ‚¯Ë̇ÏË. àÁ ÌÂÒÍÓθÍËı ÔÛÚÂÈ, Ò‚flÁ˚‚‡-
˛˘Ëı ‚¯ËÌ˚ v
j
Ë v
l
, ·Û‰ÂÏ Ò˜ËÚ‡Ú¸ ÏËÌËχθÌ˚Ï ÚÓÚ ÔÛÚ¸,
ÍÓÚÓ˚È ÒÓÒÚÓËÚ ËÁ ÏËÌËχθÌÓ„Ó ˜ËÒ· ·Â. åËÌËχθÌ˚È
êàë. 2.23

52
ÔÛÚ¸ ÏÓÊÂÚ ·˚Ú¸ Ì ‰ËÌÒÚ‚ÂÌÌ˚Ï. å‡ÍÒËχθÌ˚Ï ÔÛÚÂÏ ÏÂÊ-
‰Û ‚¯Ë̇ÏË v
j
Ë v
l
·Û‰ÂÚ ÔÛÚ¸, ÒÓ‰Âʇ˘ËÈ Ì‡Ë·Óθ¯Â ˜ËÒ-
ÎÓ Â·Â. éÌ ÚÓÊ ÏÓÊÂÚ ·˚Ú¸ Ì ‰ËÌÒÚ‚ÂÌÌ˚Ï.
ǯË̇ v
j
̇Á˚‚‡ÂÚÒfl Ò‚flÁ‡ÌÌÓÈ Ò ‚¯ËÌÓÈ v
l
, ÂÒÎË
ÏÂÊ‰Û ˝ÚËÏË ‚¯Ë̇ÏË ÒÛ˘ÂÒÚ‚ÛÂÚ Ï‡¯ÛÚ (‡ Á̇˜ËÚ, Ë ÒÛ-
˘ÂÒÚ‚ÛÂÚ ÔÛÚ¸).
í‡ÍËÏ Ó·‡ÁÓÏ, ‚¯Ë̇ v
l
fl‚ÎflÂÚÒfl ÒÓÒ‰ÌÂÈ ÔÓ ÓÚÌÓ¯Â-
Ì˲ Í ‚ ¯ËÌ v
j
, ÂÒÎË ‚¯Ë̇ v
l
Ò‚flÁ‡Ì‡ Ò ‚¯ËÌÓÈ v
j
Ò
ÔÓÏÓ˘¸˛ ÔÛÚË, ÒÓÒÚÓfl˘Â„Ó ËÁ Ó‰ÌÓ„Ó Â·‡
r
r
(v
j
, v
l
):
M(v
j
, v
l
) =
r
r
(v
j
, v
l
).
ǯËÌ˚ v
j
Ë v
l
̇Á˚‚‡˛ÚÒfl ‚Á‡ËÏÓÒ‚flÁ‡ÌÌ˚ÏË, ÂÒÎË ÒÛ-
˘ÂÒÚ‚Û˛Ú Ï‡¯ÛÚ˚ (ÔÛÚË) ÓÚ ‚¯ËÌ˚ v
j
Í ‚¯ËÌ v
l
Ë Ó·-
‡ÚÌÓ: ÓÚ ‚¯ËÌ˚ v
l
Í ‚¯ËÌ v
j
.
è Ë Ï Â 10. ç‡È‰ËÚ ‚Ò ÔÛÚË, Ò‚flÁ˚‚‡˛˘Ë ‚¯ËÌ˚ v
1
Ë v
4
‰Îfl „‡Ù‡, ËÁÓ·‡ÊÂÌÌÓ„Ó Ì‡ ËÒ. 2.20, Ë Û͇ÊËÚ ÏËÌË-
χθÌ˚È ÔÛÚ¸.
ê  ¯ Â Ì Ë Â. àÏÂÂÚÒfl ˜ÂÚ˚ ÔÛÚË:
1. è(v
1
, v
3
, v
4
);
2. è(v
1
, v
2
, v
4
);
3. è(v
1
, v
2
, v
5
, v
2
, v
4
);
4. è(v
1
, v
5
, v
2
, v
4
).
åËÌËχθÌ˚ı ÔÛÚÂÈ ‰‚‡: è(v
1
, v
3
, v
4
); è(v
1
, v
2
, v
4
); ͇Ê-
‰˚È ËÁ ÌËı ÒӉ ÊËÚ ‰‚‡ ·‡. èÛÚ¸ è(v
1
, v
3
, v
4
) ÒÓÒÚÓËÚ ËÁ
·Â
r
r
(v
1
, v
3
),
r
r
(v
3
, v
4
), ‡ ÔÛÚ¸ è(v
1
, v
2
, v
4
) – ËÁ ·Â
r
r
(v
1
, v
2
),
r
r
(v
2
, v
4
). å‡ÍÒËχθÌ˚È ÔÛÚ¸ Ó‰ËÌ: è(v
1
, v
2
, v
5
, v
2
,
v
4
); ÓÌ ÒÓ‰ÂÊËÚ ˜ÂÚ˚ ·‡. ➤
èÂÂȉÂÏ Í Í·ÒÒËÙË͇ˆËË „‡ÙÓ‚ Ë ÔÓ‰„‡ÙÓ‚ Ò ÚÓ˜ÍË
Á ÂÌËfl Ò‚flÁÂÈ ÏÂÊ‰Û Ëı ‚¯Ë̇ÏË. èÓ-ÔÂÊÌÂÏÛ Ó·ÓÁ̇-
˜ËÏ ˜ÂÂÁ V ÏÌÓÊÂÒÚ‚Ó ‚ÒÂı ‚¯ËÌ „‡Ù‡. ÅÛ‰ÂÏ Ì‡Á˚-
‚‡Ú¸ „‡Ù G(V, R) Ò‚flÁÌ˚Ï, ÂÒÎË ‰‚ β·˚ ‚¯ËÌ˚
„‡Ù‡ v
j
∈ V Ë v
l
∈ V fl‚Îfl˛ÚÒfl ‚Á‡ËÏÓÒ‚flÁ‡ÌÌ˚ÏË. ÑÛ„Ë-
ÏË ÒÎÓ‚‡ÏË, „‡Ù G(V, R) ̇Á˚‚‡ÂÚÒfl Ò‚flÁÌ˚Ï, ÂÒÎË ÏÂʉÛ
β·˚ÏË ‰‚ÛÏfl Â„Ó ‚¯Ë̇ÏË v
j
Ë v
l
ÒÛ˘ÂÒÚ‚ÛÂÚ ÔÛÚ¸ è(v
j
,...,
v
k
,..., v
l
).
èÓ‰„‡Ù G(V
1
, R
1
), ÓÔ‰ÂÎÂÌÌ˚È Ì‡ ÔÓ‰ÏÌÓÊÂÒÚ‚Â ‚¯ËÌ
V
1
⊂ V
3
̇Á˚‚‡ÂÚÒfl Á‡ÏÍÌÛÚ˚Ï (ÔÓ„ÎÓ˘‡˛˘ËÏ, ÍÓ̈‚˚Ï),
ÂÒÎË Ì ÒÛ˘ÂÒÚ‚ÛÂÚ Ï‡¯ÛÚ‡, ÒÓ‰ËÌfl˛˘Â„Ó Î˛·Û˛ ‚¯ËÌÛ
v
l
∈ V
1
ÔÓ‰„‡Ù‡ G(V
1
, R
1
) ıÓÚfl ·˚ Ò Ó‰ÌÓÈ ËÁ ‚¯ËÌ
v
k
∈
VV V V
11 1
(),= − ÔË̇‰ÎÂʇ˘ÂÈ ‰ÓÔÓÎÌÂÌ˲ ÔÓ‰„‡Ù‡
G(V
1
, R
1
).
ç‡ ËÒ. 2.24 ÛÒÎÓ‚ÌÓ ËÁÓ·‡ÊÂÌÓ ‚Ò ÏÌÓÊÂÒÚ‚Ó ‚¯ËÌ
V =
= V
1
+
V
1
Ë ‰‚‡ ÔÓ‰„‡Ù‡ G(V
1
, R
1
) Ë
G( VR
11
, ). èÓ‰„‡Ù
53
G(V
1
, R
1
) ̇Á˚‚‡ÂÚÒfl Á‡ÏÍÌÛÚ˚Ï, ÂÒÎË ÌË Ó‰Ì‡ ËÁ ‚¯ËÌ
v
k
∈
V
1
Ì fl ‚ÎflÂÚÒfl ÒÓÒ‰ÌÂÈ ÔÓ ÓÚÌÓ¯ÂÌ˲ ÌË Í Ó‰ÌÓÈ ËÁ
‚¯ËÌ v
l
∈
V
1
.
èÓ‰„‡Ù G(v
l
), ÒÓÒÚÓfl˘ËÈ ËÁ Ó‰ÌÓÈ ÍÓ̈‚ÓÈ (ÔÓ„ÎÓ˘‡˛-
˘ÂÈ) ‚¯ËÌ˚ v
l
, fl‚ÎflÂÚÒfl ÔËÏÂÓÏ Á‡ÏÍÌÛÚÓ„Ó ÔÓ‰„ ‡Ù‡ (ÒÏ.
‚¯ËÌÛ v
4
̇ ËÒ. 2.20).
èÓ‰„‡Ù G(V
1
), ÓÔ‰ÂÎÂÌÌ˚È Ì‡ ÔÓ‰ÏÌÓÊÂÒÚ‚Â ‚¯ËÌ
V
1
⊂ V
1
̇Á˚‚‡ÂÚÒfl Ò‚fl ÁÌ˚Ï, ÂÒÎË Î˛·˚ ‰‚ ‚¯ËÌ˚ v
i
∈ V
1
Ë v
j
∈ V
1
‚Á‡ËÏÓÒ‚flÁ‡Ì˚.
èÓ‰„‡Ù G(V
1
), ÓÔ‰ÂÎÂÌÌ˚È Ì‡ ÔÓ‰ÏÌÓÊÂÒÚ‚Â ‚¯ËÌ
V
1
⊂ V, ̇Á˚‚‡ÂÚÒfl ˝„Ӊ˘ÂÒÍËÏ, ÂÒÎË ÓÌ fl‚ÎflÂÚÒfl Á‡ÏÍÌÛÚ˚Ï
Ë Ò‚flÁÌ˚Ï Ó‰ÌÓ‚ÂÏÂÌÌÓ. èÓÒΉÌ ̠ËÒÍβ˜‡ÂÚ ‚ÓÁÏÓÊÌÓÒ-
ÚË Ì‡Î˘Ëfl χ¯ÛÚ‡ ËÁ ÔÓ‰„‡Ù‡
G(V
1
) ‚ ÔÓ‰„‡Ù G(V
1
).
é‰Ì‡ÍÓ Ï‡¯ÛÚ ËÁ ÔÓ‰„‡Ù‡ G(V
1
) ‚ ÔÓ‰„‡Ù
G(V
1
) ÓÚÒÛÚÒÚ-
‚ÛÂÚ, Ë ‚Ò ‚¯ËÌ˚, Ô Ë̇‰ÎÂʇ˘Ë ÔÓ‰ÏÌÓÊÂÒÚ‚Û V
1
, ‚Á‡Ë-
ÏÓÒ‚flÁ‡Ì˚.
ù„Ӊ˘ÂÒÍËÏ ÏÓÊÂÚ ·˚Ú¸ Ë ‚ÂÒ¸ „‡Ù G(V), ÓÔ‰ÂÎÂÌ-
Ì˚È Ì‡ ‚ÒÂÏ ÏÌÓÊÂÒÚ‚Â ‚¯ËÌ V. Ç ˝ÚÓÏ ÒÎÛ˜‡Â ‚Ò ‚¯ËÌ˚
„‡Ù‡ fl‚Îfl˛ÚÒfl ‚Á‡ËÏÓÒ‚flÁ‡ÌÌ˚ÏË. àÌÓ„‰‡ ÓËÂÌÚËÓ‚‡ÌÌ˚È
˝„Ӊ˘ÂÒÍËÈ „ ‡Ù ̇Á˚‚‡˛Ú ·ËÒ‚flÁ‡ÌÌ˚Ï.
èÓ‰„‡Ù G(V
1
), ÓÔ‰ÂÎÂÌÌ˚È Ì‡ ÔÓ‰ÏÌÓÊÂÒÚ‚Â ‚¯ËÌ
V
1
⊂ V, ̇Á˚‚‡ÂÚÒfl ÌÂÁ‡ÏÍÌÛÚ˚Ï, ÂÒÎË ‰Îfl β·ÓÈ ‚¯ËÌ˚
v
l
∈ V
1
ÒÛ˘ÂÒÚ‚ÛÂÚ Ï‡¯ÛÚ, Ó͇̘˂‡˛˘ËÈÒfl ‚ Ó‰ÌÓÈ ËÁ ‚Â-
¯ËÌ ÔÓ‰„‡Ù‡
G(V
1
) (ÒÏ. ËÒ. 2.22, „‰Â V
1
= {v
2
, v
3
}).
èÓ‰„‡Ù G(V
1
), ÓÔ‰ÂÎÂÌÌ˚È Ì‡ ÔÓ‰ÏÌÓÊÂÒÚ‚Â ‚¯ËÌ
V
1
⊂ V, ̇Á˚‚‡ÂÚÒfl ̇˜‡Î¸Ì˚Ï, ÂÒÎË, Ò Ó‰ÌÓÈ ÒÚÓÓÌ˚, ÌÂÚ
χ¯ÛÚ‡, ÒÓ‰ËÌfl˛˘Â„Ó Î˛·Û˛ ‚¯ËÌÛ v
k
∈
V
1
ıÓÚfl ·˚ Ò
êàë. 2.24
54
Ó‰ÌÓÈ ËÁ ‚¯ËÌ v
l
∈
V
1
, ‡ Ò ‰Û„ÓÈ ÒÚÓÓÌ˚, ÂÒÚ¸ χ¯ÛÚ,
ÒÓ‰ËÌfl˛˘ËÈ Î˛·Û˛ ‚¯ËÌÛ v
l
∈ V
1
ıÓÚfl ·˚ Ò Ó‰ÌÓÈ ËÁ
‚¯ËÌ v
k
∈
V
1
. ã˛·ÓÈ Ì‡˜‡Î¸Ì˚È ÔÓ‰„‡Ù fl‚ÎflÂÚÒfl ÌÂÁ‡ÏÍ-
ÌÛÚ˚Ï.
èÓ‰„‡Ù G(V
1
), ÓÔ‰ÂÎÂÌÌ˚È Ì‡ ÏÌÓÊÂÒÚ‚Â ‚¯ËÌ
V
1
⊂ V, fl‚ÎflÂÚÒfl Ú‡ÌÁËÚË‚Ì˚Ï, ÂÒÎË ÂÒÚ¸ χ¯ÛÚ˚, ÒÓ‰Ë-
Ìfl˛˘Ë β·˚ ‰‚ ‚¯ËÌ˚ v
k
∈
V
1
Ë v
l
∈ V
1
, ‡ Ú‡ÍÊ ÂÒÚ¸
χ¯ÛÚ, ÒÓ‰ËÌfl˛˘ËÈ Î˛·˚ ‰‚ ‚¯ËÌ˚ v
l
∈
V
1
Ë v
k
∈
V
1
.
ã˛·ÓÈ Ú‡ÌÁËÚË‚Ì˚È ÔÓ‰„‡Ù fl‚ÎflÂÚÒfl ÌÂÁ‡ÏÍÌÛÚ˚Ï.
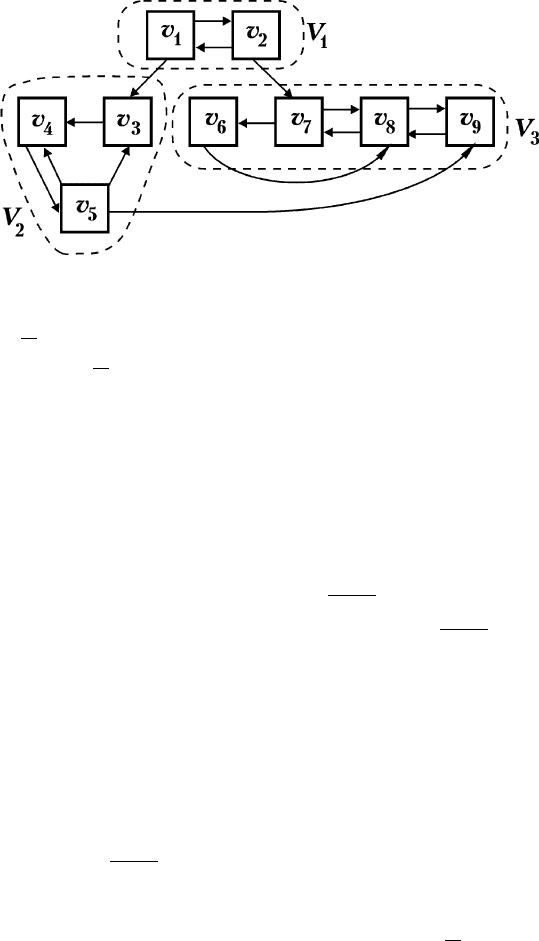
è Ë Ï Â 11. ç‡ ËÒ. 2.24 Ô‰ÒÚ‡‚ÎÂÌ Ó ËÂÌÚËÓ‚‡ÌÌ˚È
„‡Ù ÌÂÍÓÚÓÓÈ ÒËÒÚÂÏ˚ S. ì͇ÊËÚÂ, ͇ÍË ÔÓ‰„‡Ù˚ fl‚Îfl˛Ú-
Òfl Á‡ÏÍÌÛÚ˚ÏË, Ò‚flÁÌ˚ÏË, ÌÂÁ‡ÏÍÌÛÚ˚ÏË, ̇˜‡Î¸Ì˚ÏË, Ú‡ÌÁË-
ÚË‚Ì˚ÏË.
é Ú ‚  Ú. 1. èÓ‰„‡Ù G(V
1
), „‰Â V
1
= {v
1
, v
2
} fl‚ÎflÂÚÒfl ̇-
˜‡Î¸Ì˚Ï, Ú‡Í Í‡Í ÒÛ˘ÂÒÚ‚Û˛Ú Ï‡¯ÛÚ˚ ËÁ ‚¯ËÌ v
1
, v
2
‚ β·Û˛ ‚ ¯ËÌÛ v
i
∈
V
1
(
V
1
= V – V
1
), ÌÓ ÌÂÚ Ï‡¯ÛÚ‡
ËÁ β·ÓÈ ‚¯ËÌ˚ v
i
∈
V
1
(V
1
= V – V
1
) ‚ ‚¯ËÌÛ v
1
ËÎË
v
2
(v
2
∈ V
t
, v
2
∈ V
t
).
2. èÓ‰„‡Ù G(V
3
), „‰Â V
3
= {v
6
, v
7
, v
8
, v
9
}, fl‚ÎflÂÚÒfl Á‡ÏÍ-
ÌÛÚ˚Ï Ë Ò‚flÁÌ˚Ï Ó‰ÌÓ‚ÂÏÂÌÌÓ, Ú‡Í Í‡Í ÌÂÚ Ï‡¯ÛÚ‡, ‚˚-
ıÓ‰fl˘Â„Ó ËÁ β·ÓÈ ‚¯ËÌ˚ v
l
∈ V
3
(l = 6, 7, 8, 9) Ë Á‡Í‡Ì˜Ë-
‚‡˛˘Â„ÓÒfl ‚ Ó‰ÌÓÈ ËÁ ‚¯ËÌ ÏÌÓÊÂÒÚ‚‡
V
3
= V – V
3
= {v
1
,
v
2
, v
3
, v
4
, v
5
}. äÓÏ ÚÓ„Ó, β·˚ ‰‚ ‚¯ËÌ˚ ÔÓ‰„‡Ù‡ G(V
3
)
‚Á‡ËÏÓÒ‚flÁ‡Ì˚. í‡Í Í‡Í ÔÓ‰„‡Ù G(V
3
) fl‚ÎflÂÚÒfl Á‡ÏÍÌÛÚ˚Ï Ë
Ò‚flÁÌ˚Ï Ó‰ÌÓ‚ÂÏÂÌÌÓ, ÚÓ ÓÌ fl‚ÎflÂÚÒfl ˝„Ӊ˘ÂÒÍËÏ: ÒËÒÚÂχ
S, ÔÓÔ‡‚ ‚ Ó‰ÌÛ ËÁ ‚¯ËÌ ˝ÚÓ„Ó ÔÓ‰„‡Ù‡ G(V
3
), Ì ‚˚ȉÂÚ Á‡
Ô‰ÂÎ˚ ÏÌÓÊÂÒÚ‚‡ ‚¯ËÌ V
3
= {v
6
, v
7
, v
8
, v
9
}.
3. èÓ‰„‡Ù G(V
2
), „‰Â V
2
= {v
3
, v
4
, v
5
}, fl‚ÎflÂÚÒfl Ú‡ÌÁËÚË‚-
Ì˚Ï: ‚ ÔÓ‰„‡Ù G(V
2
) ÏÓÊÌÓ ÔÓÔ‡ÒÚ¸ ËÁ Ó‰ÌÓÈ ËÁ ‚¯ËÌ ÔÓ‰-
„‡Ù‡ G(V
1
) Ë ÔÂÂÈÚË ‚ Ó‰ÌÛ ËÁ ‚¯ËÌ ÔÓ‰„‡Ù‡ G(V
2
).
4. èÓ‰„‡Ù˚ G(V
1
) Ë G(V
2
) fl‚Îfl˛ÚÒfl ÌÂÁ‡ÏÍÌÛÚ˚ÏË. ➤
ÉêÄîõ Ç àçîéêåÄíàäÖ
èÓ‰ ËÌÙÓχÚËÍÓÈ ÔÓÌËχ˛Ú ÍÓÏÔÎÂÍÒ Ì‡Û˜Ì˚ı ‰ËÒˆËÔÎËÌ,
ËÁÛ˜‡˛˘Ëı Á‡ÍÓÌÓÏÂÌÓÒÚË Ò·Ó‡, Ô‰‡˜Ë Ë Ô‡·ÓÚÍË
ËÌÙÓχˆËË. ë‰ÒÚ‚‡ÏË ËÌÙÓχÚËÍË ÒÎÛÊ‡Ú ùÇå, ‡ÔÔ‡ ‡-
ÚÛ‡ Ò‚flÁË Ë Ô‰‡˜Ë ‰‡ÌÌ˚ı, ÒËÒÚÂÏ˚ ÓÚÓ·‡ÊÂÌËfl ËÌÙÓ-
χˆËË, ‡ Ú‡ÍÊ χ¯ËÌÌ˚ ‡Î„ÓËÚÏ˚ Ë ÔÓ„‡ÏÏ˚, ÏÂÚÓ‰˚
ÒʇÚËfl Ë ÍÓ‰ËÓ‚‡ÌËfl ÚÂÍÒÚÓ‚ÓÈ ËÌÙÓχˆËË Ë Ú.Ô. àÌÙÓχ-
ÚË͇ Óı‚‡Ú˚‚‡ÂÚ ‡ÁÌ˚ ӷ·ÒÚË ˜ÂÎӂ˜ÂÒÍÓÈ ‰ÂflÚÂθÌÓÒÚË,

55
Ô‰·„‡fl ÏÂÚÓ‰˚ Ë Ò‰ÒÚ‚‡ ‡‚ÚÓχÚËÁ‡ˆËË ‡Á΢Ì˚ı ÔÓ-
ˆÂÒÒÓ‚ Ô‡·ÓÚÍË ËÌÙÓχˆËË, Ú‡‰ËˆËÓÌÌÓ ÓÚÌÓÒËÏ˚ı Í
ËÌÚÂÎÎÂÍÚۇθÌÓÈ ÒÙÂÂ. àÌÙÓχˆËÓÌÌÓ-ÔÓËÒÍÓ‚˚ ÒËÒÚÂÏ˚,
‡‚ÚÓχÚËÁËÓ‚‡ÌÌ˚ ÒËÒÚÂÏ˚ Ó„‡ÌËÁ‡ˆËÓÌÌÓ„Ó ÛÔ‡‚ÎÂÌËfl,
ÒËÒÚÂÏ˚ ‡‚ÚÓχÚËÁ‡ˆËË ÔÓÂÍÚËÓ‚‡ÌËfl ÚÂıÌËÍË – ‚Ò ˝ÚÓ
ÔËÏÂ˚ Ó·˙ÂÍÚÓ‚ ÔËÍ·‰ÌÓÈ ËÌÙÓχÚËÍË.
ɇÙ˚ ËÌÙÓχˆËÓÌÌ˚ı Ó·˙ÂÍÚÓ‚. Ç ËÌÙÓχÚËÍ ¯ËÓ-
ÍÓ ÔËÏÂÌfl˛Ú „‡Ù˚ Í·ÒÒËÙË͇ˆËË Ë Ú‡ÍÒÓÌÓÏËË, ÓÔ‰Â-
ÎÂÌÌ˚ ̇‰ ÒÎÓ‚‡ÏË, ÚÂÍÒÚ‡ÏË Ë ‰Û„ËÏË ËÌÙÓχˆËÓÌÌ˚ÏË
Ó·˙ÂÍÚ‡ÏË Ë ÒËÒÚÂχÏË. èËÏÂÓÏ ÒÎÓÊÌÓÈ ËÌÙÓχˆËÓÌÌÓÈ
ÒËÒÚÂÏ˚ ÏÓÊÂÚ ÒÎÛÊËÚ¸ ÍÌËÊÌ˚È ÙÓ̉ ·Ë·ÎËÓÚÂÍË ËÎË ÒËÒ-
ÚÂχ ‰ÓÍÛÏÂÌÚÓ‚ Ë ÚÂıÌËÍÓ-˝ÍÓÌÓÏ˘ÂÒÍËı ÔÓ͇Á‡ÚÂÎÂÈ Ô‰-
ÔËflÚËfl.
è˂‰ÂÏ ÔËÏÂ˚.
è Ë Ï Â 12. ê‡ÒÒÏÓÚËÏ ·ÛÍ‚ÂÌÌ˚È ÒÓÒÚ‡‚ ÒÎÓ‚‡ ÇÇÖÑÖ-
çàÖ. Ö„Ó ÏÓÊÌÓ Ò˜ËÚ‡Ú¸ ÛÔÓfl‰Ó˜ÂÌÌ˚Ï ÍÓÚÂÊÂÏ ·ÛÍ‚
Ç Ç Ö Ñ Ö ç à Ö , ˜ÚÓ Á‡ÔËÒ˚‚‡˛Ú Í‡Í ä = (Ç, Ç, Ö, Ñ, Ö, ç, à,
Ö), ÎË·Ó ÛÔÓfl‰Ó˜ÂÌÌ˚Ï ÔÓ ‡ÎÙ‡‚ËÚÛ ÒÂÏÂÈÒÚ‚ÓÏ ·ÛÍ‚ S = {Ç,
Ç, Ñ, Ö, Ö, Ö, à, ç}, ÎË·Ó ÏÌÓÊÂÒÚ‚ÓÏ ‡Á΢Ì˚ı ·ÛÍ‚ å =
{Ç, Ñ, Ö, à, ç}. äÓÚÂÊ K, ÒÂÏÂÈÒÚ‚Ó S Ë ÏÌÓÊÂÒÚ‚Ó å ·Û‰ÛÚ
ÚÂÏfl ÏÓ‰ÂÎflÏË, ÓÔËÒ˚‚‡˛˘ËÏË ÒÎÓ‚Ó ÇÇÖÑÖçàÖ Ò Û·˚‚‡-
˛˘ÂÈ ÚÓ˜ÌÓÒÚ¸˛.
ã˛·Û˛ Ù‡ÁÛ ËÁ L ÒÎÓ‚ ÏÓÊÌÓ ‡Ì‡Îӄ˘ÌÓ ÏÓ‰ÂÎËÓ‚‡Ú¸
ÍÓÚÂÊÂÏ, ÒÂÏÂÈÒÚ‚ÓÏ ËÎË ÏÌÓÊÂÒÚ‚ÓÏ ÂÂ ÒÎÓ‚. Ç˚ÒÚÓË‚ ÒÎÓ-
‚‡ Ù‡Á˚ ‚ ‡ÎÙ‡‚ËÚÌÓÏ ÔÓfl‰Í ÓÚ 1-„Ó ‰Ó L-„Ó, ÍÓÚÂÊ, ÒÂ-
ÏÂÈÒÚ‚Ó Ë ÏÌÓÊÂÒÚ‚Ó ÒÎÓ‚ Ù‡Á˚ ÏÓÊÌÓ ÓÔËÒ‡Ú¸ ˜ËÒÎÓ‚˚Ï
‚ÂÍÚÓÓÏ, ÒÂÏÂÈÒÚ‚ÓÏ ËÎË ÏÌÓÊÂÒÚ‚ÓÏ.
è Ë Ï Â 13. Ç ÒÚÓÍ “àÇÄç Ë„ ‡ÂÚ Ì‡ Ú۷” ÒÓ‰ÂÊËÚ-
Òfl 11 ‡Á΢Ì˚ı ÒËÏ‚ÓÎÓ‚;
– ÔÓ·ÂÎ Ë 10 ·ÛÍ‚, ÍÓÚÓ˚ ‡ÒÒÚ‡‚ÎÂÌ˚ ÔÓ ‰‚‡‰ˆ‡ÚË
‡Á΢Ì˚Ï ÏÂÒÚ‡Ï. ëÓÒÚ‡‚ËÏ Ú‡·Î˘ÍÛ, ‰‡˛˘Û˛ ÌÓχ ÏÂÒÚ
ÒÚÓÍË, Á‡ÌËχÂÏ˚ı ‚ıÓ‰fl˘ËÏË ‚ Ì ÒËÏ‚Ó·ÏË:
5, 12, 15 ( – ÔÓ·ÂÎ),
‡ 3, 9, 14,
· 19,
‚ 2,
„ 7,
‡ 10, 20,
Ë 1, 6,
Ì 1, 6,
Ì 4, 13,
8, 17,
Ú 11, 16,
Û 18.
56
åÌÓÊÂÒÚ‚Ó N ÌÓÏÂÓ‚ {1, 2, 3,..., 20} ÏÂÒÚ ‚ ÒÚÓÍ Ó͇Á‡-
ÎÓÒ¸ ‡Á·ËÚ˚Ï Ì‡ Ó‰ËÌ̇‰ˆ‡Ú¸ ÌÂÔÂÂÒÂ͇˛˘ËıÒfl Í·ÒÒÓ‚,
Óڂ˜‡˛˘Ëı ÏÂÒÚ‡Ï ‡ÒÔÓÎÓÊÂÌËfl ‡Á΢Ì˚ı ÒËÏ‚ÓÎÓ‚ N =
=N
1
+ N
2
+ ... + N
11
. ùÚÓ ‡Á·ËÂÌË ÏÂÒÚ Ì‡ Í·ÒÒ˚ ÏÓÊÌÓ
Ô‰ÒÚ‡‚ËÚ¸ ÔÓÒÚ˚Ï „‡ÙÓÏ Ò ÌÓÒËÚÂÎÂÏ N Ë Â·‡ÏË, ÒÓ‰Ë-
Ìfl˛˘ËÏË ÌÓχ ÏÂÒÚ, Á‡ÌflÚ˚ı Ó‰Ë̇ÍÓ‚˚ÏË ·ÛÍ‚‡ÏË.
ì Ô ‡ Ê Ì Â Ì Ë Â. ç‡ËÒÛÈÚ ÔÓÎÛ˜ÂÌÌ˚È „‡Ù. ëÍÓθÍÓ ‚
ÌÂÏ ÚËÔÓ‚ ˜‡ÒÚÂÈ? ➤
ç‡fl‰Û Ò ÔÓÒÚ˚ÏË „‡Ù‡ÏË ËÁÛ˜‡˛ Ú Ë Ú‡Í Ì‡Á˚‚‡ÂÏ˚Â
ÏÛθÚË„‡Ù˚, ‚ ÍÓÚÓ˚ı ÌÂÍÓÚÓ˚ ԇ˚ ‚¯ËÌ ÒÓ‰ËÌfl˛ÚÒfl
Ì ӉÌËÏ, ‡ ÌÂÒÍÓθÍËÏË Ô‡‡ÎÎÂθÌ˚ÏË Â·‡ÏË.
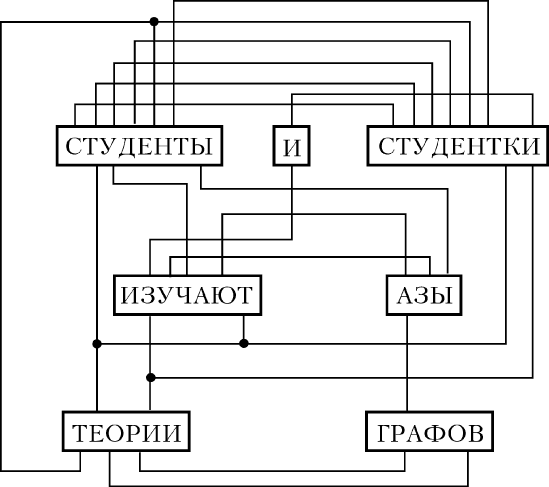
è Ë Ï Â 1 4 . èÓÒÚÓËÏ ÏÛθÚË„‡Ù ÔÓ Ù‡Á “ëÚÛ‰ÂÌÚ˚ Ë
ÒÚÛ‰ÂÌÚÍË ËÁÛ˜‡˛Ú ‡Á˚ ÚÂÓËË „‡ÙÓ‚”. Ç ˝ÚÓÈ Ù‡Á 7 ÒÎÓ‚,
Ó·‡ÁÛ˛˘Ëı ‚¯ËÌ˚ 1, 2, 3, 4, 5, 6, 7. è‡Û ÒÎÓ‚, Ò͇ÊÂÏ, 4
(ËÁÛ˜‡˛Ú) Ë 5 (‡Á˚) ÒÓ‰ËÌËÏ ‰‚ÛÏfl Ô‡‡ÎÎÂθÌ˚ÏË Â·‡ÏË,
ÓÚϘÂÌÌ˚ÏË ·ÛÍ‚‡ÏË, ‚ıÓ‰fl˘ËÏË ‚ Ó·‡ ÒÎÓ‚‡ (Û Ì‡Ò ˝ÚÓ “‡” Ë
“Á”). ÖÒÎË ÒÓ‰ËÌËÚ¸ Í‡Ê‰Û˛ Ô‡Û ÒÎÓ‚ ·‡ÏË, ÔÓϘÂÌÌ˚ÏË
Ó·˘ËÏË ‰Îfl ÌËı ·ÛÍ‚‡ÏË, ÚÓ ÔÓÎÛ˜ËÚÒfl ÏÛθÚË„‡Ù å
Ù
, ËÁÓ·-
‡ÊÂÌÌ˚È Ì‡ ËÒ. 2.25. Ç ÌÂÏ ‚¯ËÌ˚ ÔÓϘÂÌ˚ ÒÎÓ‚‡ÏË,
˜ÚÓ ÔÓÁ‚ÓÎflÂÚ ËÁ·Âʇڸ ÔÓÏÂÚÍË Â·Â Û͇Á‡ÌËÂÏ Ì‡ ·ÛÍ‚˚
ÒÎÓ‚‡.
ëӷˇfl ‚ÏÂÒÚ ÌÓχ ÒÎÓ‚, ÒÓ‰Âʇ˘Ëı ‰‡ÌÌÛ˛ ·ÛÍ‚Û,
ÔÓÎÛ˜ËÏ ÒÎÂ‰Û˛˘Û˛ Ú‡·ÎËˆÛ ÒÓÓÚ‚ÂÚÒÚ‚Ëfl ·ÛÍ‚‡
–
ÒÓ‰Âʇ˘ËÂ
 ÒÎÓ‚‡:
1. ‡ 4, 5, 7 9. Ì 1, 3
2. ‚ 7 10. Ó 6, 7
3. „ 7 11. Ò 1, 3
4. ‰ 1, 3 12. Ú 1, 3, 4, 6
5. Â 1, 3, 6 13. Û 1, 3, 4
6. Á 4, 5 14. ˚ 1, 7
7. Ë 2, 3, 4, 5 15. Ù 7
8. Í 3
å˚ ‚ˉËÏ, ˜ÚÓ ‡ÁϘÂÌÌ˚È ÏÛθÚË„‡Ù ÏÓÊÌÓ ËÒÔÓθÁÓ-
‚‡Ú¸ ‰Îfl ‡ÁÎÓÊÂÌËfl Â„Ó ÌÓÒËÚÂÎfl (ÏÌÓÊÂÒÚ‚‡ ÒÎÓ‚ Ù‡Á˚) ̇
Ú‡Í Ì‡Á˚‚‡ÂÏ˚ ڇÍÒÓÌ˚ („ÛÔÔ˚ ÒÎÓ‚, ÒÓ‰Âʇ˘ Ëı ÙËÍÒËÓ-
‚‡ÌÌÛ˛ ·ÛÍ‚Û), ÍÓÚÓ ˚ ‚ ÒÓ‚ÓÍÛÔÌÓÒÚË Ó·‡ÁÛ˛Ú ÔÓÍ˚ÚËÂ
ÌÓÒËÚÂÎfl. çÂÍÓÚÓ˚ ËÁ Ú‡ÍÒÓÌÓ‚, ̇ÔËÏ “Ë” = (2, 3, 4,
6) Ë “Û” = (1, 3, 4) ËÏÂ˛Ú Ó·˘Û˛ ˜‡ÒÚ¸ 3, 4 (ÒÚÛ‰ÂÌÚÍË, ËÁÛ-
˜‡˛Ú), ‰Û„Ë Ì ÔÂÂÒÂ͇˛ÚÒfl, ̇ÔËÏ “‰” = (1, 3) Ë “Ó” =
= (6, 7). ➤
åÛθÚË„‡Ù Á‡‰‡ÂÚ Ú‡ÍÒÓÌÓÏ˲ ÒÎÓ‚ Ù‡Á˚ ÔÓ ÔËÁ̇ÍÛ
‚ıÓ‰ËÏÓÒÚË ·ÛÍ‚˚ ‚ ÒÎÓ‚Ó. ä‡Ê‰Ó ÒÎÓ‚Ó ÔÓÔ‡‰‡ÂÚ ‚Ó ÒÚÓθÍÓ
Ú‡ÍÒÓÌÓ‚, ÒÍÓθÍÓ ‚ ÌÂÏ ‡Á΢Ì˚ı ·ÛÍ‚. í‡ÍÒÓÌ˚ Ì ‰‡˛Ú
57
‡Á·ËÂÌËfl ËÎË Í·ÒÒËÙË͇ˆËË ÏÌÓÊÂÒÚ‚‡ ÒÎÓ‚ Ù‡Á˚, ÌÓ ‰‡-
˛Ú ‚ÓÁÏÓÊÌÓÒÚ¸ ÔÓËÒ͇ ÒÎÓ‚‡ ÔÓ ‚ıÓ‰fl˘ËÏ ‚ ÌÂ„Ó ·ÛÍ‚‡Ï.
Ä̇Îӄ˘ÌÓ ÏÓÊÌÓ Ó„‡ÌËÁÓ‚‡Ú¸ ÔÓËÒÍ Ù‡Á ÔÓ ‚ıÓ‰fl˘ËÏ ‚
ÌËı ÒÎÓ‚‡Ï, ‡ Ú‡ÍÊ ÚÂÍÒÚÓ‚ (ÒÚ‡ÚÂÈ) ÔÓ ‚ıÓ‰fl˘ËÏ ‚ ÌËı Ù‡-
Á‡Ï ÔÛÚÂÏ ÔÓÒÚÓÂÌËfl ÏÛθÚË„‡Ù‡ ‚ıÓ‰ËÏÓÒÚË ˝ÎÂÏÂÌÚÓ‚ ‚
Ó·˙ÂÍÚ˚. åÛθÚË„‡Ù˚ ¯ËÓÍÓ ÔËÏÂÌfl˛Ú ‚ ÔÓÒÚÓÂÌËË ËÌ-
ÙÓχˆËÓÌÌÓ-ÔÓËÒÍÓ‚˚ı ÒËÒÚÂÏ.
ê‡ÁϘÂÌÌ˚È ÏÛθÚË„‡Ù Ù‡Á˚ ÏÓÊÌÓ Ú‡ÍÚÓ‚‡Ú¸ ͇Í
Ó·Ó·˘ÂÌÌ˚È „‡Ù, ËÎË ÏÓ‰ÂθÌ˚È „‡Ù. åÓ‰ÂθÌ˚Ï „‡ÙÓÏ
·Û‰ÂÏ Ì‡Á˚‚‡Ú¸ ÌÂÍÓÚÓÓ ÏÌÓÊÂÒÚ‚Ó V (‡ÎÙ‡‚ËÚ) Ò ‚˚‰ÂÎÂÌ-
ÌÓÈ Ì‡ ÌÂÏ ÒËÒÚÂÏÓÈ ÒÎÓ‚ (ˆÂÔÓ˜ÂÍ ·ÛÍ‚) ÍÓ̘ÌÓÈ ‰ÎËÌ˚.
é·ÓÁ̇˜‡fl ˜ÂÂÁ R
k
ÒÓ‚ÓÍÛÔÌÓÒÚ¸ k ·ÛÍ‚ÂÌÌ˚ı ÒÎÓ‚ ÏÓ‰ÂÎË,
ÏÓ‰Âθ ‚ ˆÂÎÓÏ Á‡‰‡˛Ú Í‡Í ÒËÒÚÂÏÛ ÒÎÓ‚ ÏÓ‰ÂÎË M = 〈V; R
1
,
R
2
,..., R
L
〉, ‚Íβ˜‡˛˘Û˛ ÓÒÌÓ‚‡ÌË V Ë Ò˄̇ÚÛÛ ÏÓ‰ÂÎË R =
= R
1
∪R
2
∪... ∪R
L
(ÒÓ‚ÓÍÛÔÌÓÒÚ¸ ‚ÒÂı  ÒÎÓ‚-ˆÂÔÓ˜ÂÍ). ë˜ËÚ‡fl
ÒÎÓ‚Ó r ∈ R
k
“·ÓÏ” k-„Ó ÔÓfl‰Í‡, ÏÓÊÌÓ ÛÔÓ‰Ó·ËÚ¸ ÏÓ‰Âθ å
„ËÔ„‡ÙÛ, ‚ ÍÓÚÓÓÏ ÍÓÏ ÒÎÓ‚ ‰ÎËÌ˚ 1 (‚¯ËÌ) Ë ‰ÎËÌ˚
2 (Ó·˚˜Ì˚ı ·Â) ‰ÓÔÛÒÚËÏ˚ ·‡ k-„Ó (k ≤ L) ÔÓfl‰Í‡: ÒÎÓ-
‚‡ ‰ÎËÌ˚ k ̇‰ ‡ÎÙ‡‚ËÚÓÏ V.
êàë. 2.25
