Овчаров Л.А. и др. Математические модели информационых процессов и управления
Подождите немного. Документ загружается.


38
1. ä‡Ê‰‡fl Ô‡‡ (a, a), „‰Â ‡ ∈ Ä, fl‚ÎflÂÚÒfl ˝ÎÂÏÂÌÚÓÏ ÏÌÓ-
ÊÂÒÚ‚‡ Ä
ϕ
– ÂÙÎÂÍÒË‚ÌÓÒÚ¸.
2. ÖÒÎË Ô‡ ‡ (a, b) ∈ A
ϕ
Ë Ô‡‡ (b, c) ∈ A
ϕ
, ÚÓ Ë Ô‡‡
(a, c) ∈ A
ϕ
– Ú‡ÌÁËÚË‚ÌÓÒÚ¸.
3. ÖÒÎË
ab ba
˜˜
,ϕϕ Ë ÚÓ
a = b – ‡ÌÚËÒËÏÏÂÚ˘ÌÓÒÚ¸.
ó‡ÒÚ˘ÌÓ ÛÔÓfl‰Ó˜ÂÌÌÛ˛ Ô‡Û (a, b) ∈ A
ϕ
Ó·ÓÁ̇˜‡˛Ú a ≤ b.
Ç Í‡˜ÂÒÚ‚Â ˜‡ÒÚ˘ÌÓÈ ÛÔÓfl‰Ó˜ÂÌÌÓÒÚË ÏÌÓÊÂÒÚ‚‡ Ä ÏÓÊÌÓ
‡ÒÒχÚË‚‡Ú¸ ·Ë̇ÌÓ ÓÚÌÓ¯ÂÌË ÚÓʉÂÒÚ‚‡ Ö(a E b), ÍÓ„‰‡
‡ = b.
è Ë Ï Â 4. ê‡ÒÒχÚË‚‡ÂÚÒfl ÏÌÓÊÂÒÚ‚Ó Ä ‚ÒÂı ÒÚÛ‰ÂÌÚÓ‚
ÒÔˆˇθÌÓÒÚË 22.02 ÔÓÒΠӘ‰ÌÓÈ ÒÂÒÒËË, ÍÓÚÓÓ ‡Á·ËÚÓ
̇ ˜ÂÚ˚ Í·ÒÒ‡:
Ä
1
– ÒÚÛ‰ÂÌÚ˚, Ò‰‡‚¯Ë ˝ÍÁ‡ÏÂÌ˚ ÚÓθÍÓ Ì‡ ÔflÚ¸;
Ä
2
– ÒÚÛ‰ÂÌÚ˚, Ò‰‡‚¯Ë ˝ÍÁ‡ÏÂÌ˚ ̇ ˜ÂÚ˚Â Ë ÔflÚ¸;
Ä
3
– ÒÚÛ‰ÂÌÚ˚, ÔÓÎۘ˂¯Ë ̇ ˝ÍÁ‡ÏÂ̇ı ıÓÚfl ·˚ Ó‰ÌÛ
ÚÓÈÍÛ, ÌÓ ÌË Ó‰ÌÓÈ ‰‚ÓÈÍË;
Ä
4
– ÒÚÛ‰ÂÌÚ˚, ÔÓÎۘ˂¯Ë ̇ ˝ÍÁ‡ÏÂ̇ı ıÓÚfl ·˚ Ó‰ÌÛ
‰‚ÓÈÍÛ.
í‡ÍËÏ Ó·‡ÁÓÏ, ‚Ò ÏÌÓÊÂÒÚ‚Ó Ä ‡Á·Ë‚‡ÂÚÒfl ̇ 4 Í·ÒÒ‡:
Ä
1
, Ä
2
, Ä
3
, Ä
4
(ÒÏ. ËÒ. 1.15).
ê‡ÒÒÏÓÚËÏ ÒÎÂ‰Û˛˘Ë ÔÓ‰ÏÌÓÊÂÒÚ‚‡: Ç
1
= Ä
2
+ Ä
3
+ Ä
4
–
ÒÚÛ‰ÂÌÚ˚, Ò‰‡‚¯Ë ˝ÍÁ‡ÏÂÌ˚ Ì ÚÓθÍÓ Ì‡ 5 (Ç
1
= Ä – Ä
1
=
=
Ä
1
: ÔÓ‰ÏÌÓÊÂÒÚ‚Ó Ç
1
fl‚ÎflÂÚÒfl ‰ÓÔÓÎÌÂÌËÂÏ ÔÓ‰ÏÌÓÊÂÒÚ‚‡
Ä
1
); Ç
2
= Ä
3
+ Ä
4
– ÒÚÛ‰ÂÌÚ˚, ÔÓÎۘ˂¯Ë ̇ ˝ÍÁ‡ÏÂ̇ı ıÓÚfl
·˚ Ó‰ÌÛ ‰‚ÓÈÍÛ ËÎË ıÓÚfl ·˚ Ó‰ÌÛ ÚÓÈÍÛ; Ç
3
– ÒÚÛ‰ÂÌÚ˚, ÔÓÎÛ-
˜Ë‚¯Ë ̇ ˝ÍÁ‡ÏÂ̇ı ıÓÚfl ·˚ Ó‰ÌÛ ‰‚ÓÈÍÛ.
é˜Â‚ˉÌÓ, ˜ÚÓ ËÏÂÂÚ ÏÂÒÚÓ ÒÓÓÚÌÓ¯ÂÌË Ç
3
⊂ Ç
2
⊂ Ç
1
.
èÓ‰ÏÌÓÊÂÒÚ‚‡ Ç
1
, Ç
2
, Ç
3
– ˜‡ÒÚ˘ÌÓ ÛÔÓfl‰Ó˜ÂÌ˚. ùÚÓ ÛÚ-
‚ÂʉÂÌË ÏÓÊÌÓ Á‡ÔËÒ‡Ú¸ Ú‡Í:
Ç
3
≤ Ç
2
≤ Ç
1
.
åÂÊ‰Û Î˛·˚ÏË ˝ÎÂÏÂÌÚ‡ÏË ‡ Ë b ˝ÚËı ÔÓ‰ÏÌÓÊÂÒÚ‚ ÒÛ˘Â-
ÒÚ‚ÛÂÚ ˜‡ÒÚ˘ÌÓ ÛÔÓfl‰Ó˜ÂÌËÂ. ç‡ÔËÏÂ, ÂÒÎË ‡ ∈ Ç
2
Ë
b ∈ B
3
, ÚÓ ‡ > b; ÂÒÎË ˝ÎÂÏÂÌÚ˚ ‡ Ë b ÔË̇‰ÎÂÊ‡Ú ÔÓ‰ÏÌÓÊÂ-
ÒÚ‚Û (̇ÔËÏÂ, Ç
1
), ÚÓ ËÏÂÂÚ ÏÂÒÚÓ ‡‚ÂÌÒÚ‚Ó ‡ = b. ➤
êàë. 1.15

39
2.1. éëçéÇçõÖ èéçüíàü íÖéêàà ÉêÄîéÇ
é‰ÌËÏ ËÁ ÔflÏ˚ı Îӄ˘ÂÒÍËı ÔÓ‰ÓÎÊÂÌËÈ ÚÂÓËË ÏÌÓ-
ÊÂÒÚ‚ fl‚ÎflÂÚÒfl ÚÂÓËfl „‡ÙÓ‚, ˝ÎÂÏÂÌÚ˚ ÍÓÚÓÓÈ Ï˚ Ô‰-
ÒÚ‡‚ÎflÂÏ ‚ ˝ÚÓÈ „·‚Â. éÒÌÓ‚˚ ÚÂÓËË „‡ÙÓ‚ ·˚ÎË Á‡ÎÓÊÂÌ˚
‚ÂÎËÍËÏ Ï‡ÚÂχÚËÍÓÏ ùÈÎÂÓÏ ‚ Â„Ó ¯ËÓÍÓ ËÁ‚ÂÒÚÌ˚ı ËÒÒÎÂ-
‰Ó‚‡ÌËflı Ó äÂÌ˄ҷ„ÒÍËı ÏÓÒÚ‡ı
1
, ÓÍÓÎÓ ÍÓÚÓ˚ı ‡ÒÔÓÎÓ-
ÊÂÌ ÛÌË‚ÂÒËÚÂÚ, „‰Â ‰ÎËÚÂθÌÓ ‚ÂÏfl ‡·ÓڇΠùÈÎÂ.
è‰ÏÂÚÓÏ ËÁÛ˜ÂÌËfl ‚ ÚÂÓËË „‡ÙÓ‚ fl‚Îfl˛ÚÒfl ‡Á΢Ì˚Â
ÒıÂÏ˚ (˜ÂÚÂÊË), ÒÓÒÚÓfl˘Ë ËÁ Í‚‡‰‡ÚËÍÓ‚ (ÚÓ˜ÂÍ, ÍÛÊÍÓ‚)
Ë ÒÓ‰ËÌfl˛˘Ëı ÍË‚˚ı (ËÎË ÔflÏ˚ı). 䂇‰‡ÚËÍË Ï˚ ·Û‰ÂÏ
̇Á˚‚‡Ú¸ ‚¯Ë̇ÏË „‡Ù‡; ‚Ò ÏÌÓÊÂÒÚ‚Ó ˝ÚËı ‚ ¯ËÌ Ó·Ó-
Á̇˜ËÏ V. éÌÓ ÏÓÊÂÚ ·˚Ú¸ ÍÓ̘Ì˚Ï ËÎË ·ÂÒÍÓ̘Ì˚Ï (ÌÓ
Ò˜ÂÚÌ˚Ï). ǯËÌ˚ „‡Ù‡ ÏÓ„ÛÚ ËÏÂÚ¸ Ò‡ÏÛ˛ ÔÓËÁ‚ÓθÌÛ˛
ÔËÓ‰Û (χ¯ËÌ˚, β‰Ë, ˜‡ÒÚË ÒÛ¯Ë, ÊÂÎÂÁÌÓ‰ÓÓÊÌ˚ ÛÁÎ˚,
ËÌÙÓχˆËfl, ùÇå Ë Ú.Ô). ä‡Ê‰˚ È ˝ÎÂÏÂÌÚ ÏÌÓÊÂÒÚ‚‡ V
(Í‡Ê‰Û˛ ÓÚ‰ÂθÌÛ˛ ‚¯ËÌÛ) Ï˚ ·Û‰ÂÏ Ó·ÓÁ̇˜‡Ú¸ χÎ˚ÏË
·ÛÍ‚‡ÏË: v
1
, v
2
,... (v
1
∈ V; v
2
∈ V). èflÏ˚ (ËÎË ÍË‚˚Â), ÒÓ-
‰ËÌfl˛˘Ë ˝ÚË ‚¯ËÌ˚, ·Û‰ÂÏ Ì‡Á˚‚‡Ú¸ ·‡ÏË (ËÎË ‰Û„‡-
ÏË). åÌÓÊÂÒÚ‚Ó Â·Â ·Û‰ÂÏ Ó·ÓÁ̇˜‡Ú¸ ·ÛÍ‚ÓÈ R (ËÎË Ö).
ê·Ó, ÒÓ‰ËÌfl˛˘Â ‚¯ËÌÛ v
i
Ò ‚¯ËÌÓÈ v
j
, ·Û‰ÂÏ Ó·ÓÁ̇-
˜‡Ú¸ Ú‡Í:
r(v
i
, v
j
) = r
ij
(ËÎË e
ij
).
íÓ„‰‡ „‡ÙÓÏ G = G(V, R) ·Û‰ÂÏ Ì‡Á˚‚‡Ú¸ ÏÌÓÊÂÒÚ‚Ó ‚Â-
¯ËÌ V, ̇ ÍÓÚÓÓÏ Á‡‰‡ÌÓ ·Ë̇ÌÓ ÓÚÌÓ¯ÂÌËÂ
r(v
i
, v
j
) (v
i
∈ V; v
j
∈ V), (2.1)
Û͇Á˚‚‡˛˘Â ̇ ÚÓ, ˜ÚÓ ‚¯ËÌ˚ v
i
Ë v
j
ÒÓ‰ËÌÂÌ˚ ·ÓÏ r
ij
.
ÖÒÎË Â·Ó fl‚ÎflÂÚÒfl ÌÂÓËÂÌÚËÓ‚‡ÌÌ˚Ï, ÚÓ Ì‡ ÒıÂÏ ÌÂ
·Û‰ÂÚ ÌË͇ÍËı Û͇Á‡ÌËÈ Ó ÚÓÏ, Í‡Í ÒÓ‰ËÌÂÌ˚ ‚¯ËÌ˚ v
i
Ë v
j
;
1
äÂÌ˄ҷ„ÒÍË ÏÓÒÚ˚ Ë Ì˚Ì ÒÚÓfl Ú ‚ „. ä‡ÎËÌËÌ„‡‰Â (·˚‚¯ËÈ „ÓÓ‰
äÂÌ˄ҷ„).
40
Ú‡ÍÓÂ Â·Ó ·Û‰ÂÏ Ì‡Á˚‚‡Ú¸ ÌÂÓËÂÌÚËÓ‚‡ÌÌ˚Ï Ë Ó·ÓÁ̇˜‡Ú¸
Ú‡Í:
r(v
i
, v
j
) = r(v
j
, v
i
). (2.2)
ɇÙ, Ëϲ˘ËÈ ÚÓθÍÓ Ì Â Ó Ë Â Ì Ú Ë Ó ‚ ‡ Ì Ì ˚  ·‡, ·Û‰ÂÏ
̇Á˚‚‡Ú¸ ÌÂÓËÂÌÚËÓ‚‡ÌÌ˚Ï „‡ÙÓÏ Ë Ó·ÓÁ̇˜‡Ú¸ G(V, R).
óËÒÎÓ ‚¯ËÌ n ·Û‰ÂÚ ÓÔ‰ÂÎflÚ¸Òfl ˜ÂÂÁ ÏÌÓÊÂÒÚ‚Ó ‚ -
¯ËÌ: n = V , ‡ ˜ËÒÎÓ Â·Â m – ˜ÂÂÁ ÏÌÓÊÂÒÚ‚Ó Â·Â: m =
= R.
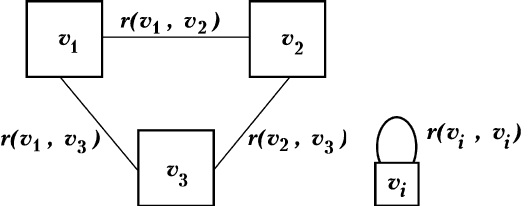
ç‡ ËÒ 2.1 ÔÓ͇Á‡Ì ÌÂÓËÂÌÚËÓ‚‡ÌÌ˚È „‡Ù G, ÒÓÒÚÓfl˘ËÈ
ËÁ ÚÂı ‚¯ËÌ (v
1
, v
2
, v
3
) Ë ÚÂı ÌÂÓËÂÌÚËÓ‚‡ÌÌ˚ı ·Â
(r(v
1
, v
2
), r(v
2
, v
3
), r(v
1
, v
3
)).
ǯËÌ˚ v
i
Ë v
j
̇Á˚‚‡˛ÚÒfl ÍÓ̈‡ÏË Â·‡ r(v
i
, v
j
) (v
i
,
v
j
∈ V). ç‡ ËÒ. 2.1 ‚Ò ‚¯ËÌ˚ ÒÓ‰ËÌÂÌ˚ ·‡ÏË.
Ç ·Óθ¯ËÌÒÚ‚Â Ô‡ÍÚ˘ÂÒÍËı ÔËÎÓÊÂÌËÈ ÚÂÓËË „‡ÙÓ‚
ÔË ËÒÒΉӂ‡ÌËË Ï‡ÚÂχÚ˘ÂÒÍËı ÏÓ‰ÂÎÂÈ ËÌÙÓχˆËÓÌÌ˚ı
ÔÓˆÂÒÒÓ‚ Ë ÛÔ‡‚ÎÂÌËfl Ì‡Ò ·Û‰ÂÚ ËÌÚÂÂÒÓ‚‡Ú¸ ‚ÓÔÓÒ Ó ÚÓÏ,
Í‡Í ÔÓËÒıÓ‰ËÚ ÒÓ‰ËÌÂÌË ‚¯ËÌ Ò ÔÓÏÓ˘¸˛ ·Â.
çÂÓËÂÌÚËÓ‚‡ÌÌÓÂ Â·Ó r(v
i
, v
j
) Û͇Á˚‚‡ÂÚ Ì‡ ÚÓ, ˜ÚÓ
ÏÂÊ‰Û ‚¯Ë̇ÏË v
i
Ë v
j
ÛÒÚ‡ÌÓ‚ÎÂÌ˚ ÒËÏÏÂÚ˘Ì˚ ·Ë̇Ì˚Â
ÓÚÌÓ¯ÂÌËfl Ë ÏÓÊÌÓ Ì ÔËÌËχڸ ‚Ó ‚ÌËχÌË ÔÓfl‰ÓÍ ‡ÒÔÓ-
ÎÓÊÂÌËfl ÍÓ̈ӂ ·‡ (‚¯ËÌ v
i
Ë v
j
).
èÂÚÎÂÈ Ì‡Á˚‚‡ÂÚÒfl ·Ó, Û ÍÓÚÓÓ„Ó Ó·Â ÍÓ̈‚˚ ‚¯Ë-
Ì˚ ÒÓ‚Ô‡‰‡˛Ú (ËÒ. 2.2). èÂÚβ y i-È ‚¯ËÌ˚ ·Û‰ÂÏ Ó·ÓÁ̇-
˜‡Ú¸ r(v
i
,
v
i
).
í‡Í Í‡Í ÍÓ̈˚ ÔÂÚÎË ÒÓ‚Ô‡‰‡˛Ú,
ÚÓ
ÌÂÚ
ÒÏ˚Ò· „Ó-
‚ÓËÚ¸
Ó
ÌÂÓËÂÌÚËÓ‚‡ÌÌÓÒÚË ËÎË ÓËÂÌÚËÓ‚‡ÌÌÓÒÚË
ÔÂÚÎË.
ÑÎfl ÌÂÓËÂÌÚËÓ‚‡ÌÌÓ„Ó Â·‡ r(v
i
, v
j
) ‚¯ËÌ˚ v
i
Ë v
j
̇-
Á˚‚‡˛ÚÒfl ÒÓ‰ËÌÂÌËflÏË.
è Ë Ï Â 1. Ç „ÓӉ ËÏÂÂÚÒfl ¯ÂÒÚ¸ ‡Á΢Ì˚ı Á‡‚Ó‰Ó‚
(Á‡ÌÛÏÂÓ‚‡ÌÌ˚ı ˜ËÒ·ÏË 1, 2, 3, 4, 5, 6), ÌÂÍÓÚÓ˚ ËÁ Á‡‚Ó-
‰Ó‚ Ó·ÏÂÌË‚‡˛ÚÒfl Ò‚ÓÂÈ ÔÓ‰Û͈ËÂÈ ÔÓ ÍÓÓÔ‡ˆËË. ëÓ‰ËÌËÏ
·‡ÏË ‚¯ËÌ˚, Ô‰ÒÚ‡‚Îfl˛˘Ë Á‡‚Ó‰˚, Ò‚flÁ‡ÌÌ˚ ÔÓ ÍÓ-
ÓÔ‡ˆËË. èÛÒÚ¸ ‚ „ÓӉ ӷÏÂÌË‚‡˛ ÚÒfl ÏÂÊ‰Û ÒÓ·ÓÈ ÔÓ‰ÛÍ-
êàë. 2.1 êàë. 2.2

41
ˆËÂÈ Ô‚˚È, ˜ÂÚ‚ÂÚ˚È Ë ÔflÚ˚È Á‡‚Ó‰˚, ‡ Ú‡ÍÊ ‚ÚÓÓÈ Ë
ÚÂÚËÈ. òÂÒÚÓÈ Á‡‚Ó‰ ‡·ÓÚ‡ÂÚ ‡‚ÚÓÌÓÏÌÓ. ëıÂχÚ˘ÂÒÍËÈ
„‡Ù G
1
, ÓÔËÒ˚‚‡˛˘ËÈ ÍÓÓÔ‡ÚË‚Ì˚ ‚Á‡ËÏÓÒ‚flÁË Á‡‚Ó‰Ó‚ ‚
„ÓÓ‰Â, Ô‰ÒÚ‡‚ÎÂÌ Ì‡ ËÒ. 2.3. àÁ ËÒÛÌ͇ ‚ˉÌÓ, ˜ÚÓ „‡Ù
“ÔÓÒÚ‡‚ÍË ÔÓ ÍÓÓÔ‡ˆËË ‚ „ÓӉ” ‡ÒÔ‡‰‡ÂÚÒfl ̇ ÚË ˜‡ÒÚË:
ÚÂÛ„ÓθÌËÍ Ò ‚¯Ë̇ÏË v
1
, v
4
, v
5
, Â·Ó Ò ‚¯Ë̇ÏË v
2
, v
3
Ë ËÁÓÎËÓ‚‡ÌÌÛ˛ ‚¯ËÌÛ v
6
.
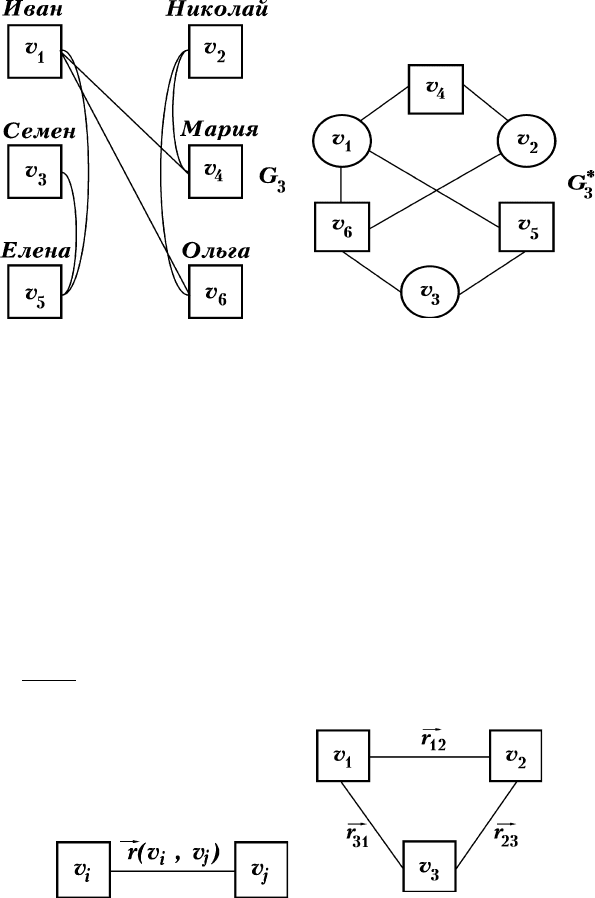
è Ë Ï Â 2. ç‡ ËÒ. 2.4 Ô‰ÒÚ‡‚ÎÂÌ „‡Ù G
2
Ò ¯ÂÒÚ¸˛
‚¯Ë̇ÏË: v
1
, v
2
, v
3
, v
4
, v
5
, v
6
Ë ‚ÓÒÂϸ˛ ÌÂÓËÂÌÚËÓ‚‡ÌÌ˚-
ÏË Â·‡ÏË r
12
= r(v
1
, v
2
), r
13
= r(v
1
, v
3
): r
14
= r(v
1
, v
4
); r
23
=
= r(v
2
, v
3
), r
26
= r(v
2
, v
6
), r
45
= r(v
4
, v
5
); r
56
= r(v
5
, v
6
). åÓÊÌÓ
Ò˜ËÚ‡Ú¸, ̇ÔËÏÂ, ˜ÚÓ ˝ÚÓ ÒËÒÚÂχ ‚ÓÒ¸ÏË ‰ÓÓ„, ÒÓ‰ËÌfl˛-
˘Ëı ¯ÂÒÚ¸ ̇ÒÂÎÂÌÌ˚ı ÔÛÌÍÚÓ‚.
è Ë Ï Â 3. ç‡ ËÒ. 2.5 Ô˂‰ÂÌ˚ ‰‚‡ ÒıÂχÚ˘ÂÒÍË ‡Á-
Ì˚ı ËÁÓ·‡ÊÂÌËfl Ó‰ÌÓ„Ó Ë ÚÓ„Ó Ê „‡Ù‡ G
3
, Ô‰ÒÚ‡‚Îfl˛˘Â-
„Ó ÒÚÛÍÚÛÛ ‚Á‡ËÏÌ˚ı ÒËÏÔ‡ÚËÈ ‚ „ÛÔÔÂ, ÒÓÒÚÓfl˘ÂÈ ËÁ ÚÂı
ÒÚÛ‰ÂÌÚÓ‚ Ë ÚÂı ÒÚÛ‰ÂÌÚÓÍ. ç‡ ÒıÂÏ 2.5, · ˛ÌÓ¯Ë ËÁÓ·‡-
ÊÂÌ˚ ÍÛÊ͇ÏË, ‡ ‰Â‚Û¯ÍË – Í‚‡‰‡ÚË͇ÏË. ë‚flÁË ÔÓ ÒËÏÔ‡-
ÚËË, Ô‰ÒÚ‡‚ÎÂÌÌ˚ ˝ÚÓÈ ‰Ë‡„‡ÏÏÓÈ, ÒÓ‰ËÌfl˛Ú ÚÓθÍÓ ˛ÌÓ-
¯ÂÈ Ò ‰Â‚ۯ͇ÏË. ä‡Ê‰ÓÂ Â·Ó „‡Ù‡
G
3
∗
ËÏÂÂÚ ‚ Ó‰ÌÓÏ ÍÓÌ-
ˆÂ ÍÛÊÓÍ, ‡ ‚ ‰Û„ÓÏ – Í‚‡‰‡ÚËÍ. á̇˜ËÚ, ÏÌÓÊÂÒÚ‚Ó ‚Â-
êàë. 2.3
êàë. 2.4
42
¯ËÌ ˝ÚÓ„Ó „‡Ù‡ ‡ÒÔ‡‰‡ÂÚÒfl ̇ ‰‚‡ ÌÂÔÂÂÒÂ͇˛˘ËıÒfl ÔÓ‰-
ÏÌÓÊÂÒÚ‚‡, ‡ ·‡ ÒÓ‰ËÌfl˛Ú ÚÓθÍÓ ‚¯ËÌ˚ ËÁ ‡ÁÌ˚ı
ÔÓ‰ÏÌÓÊÂÒÚ‚. í‡ÍË „‡Ù˚ ̇Á˚‚‡˛ÚÒfl ‰‚Û‰ÓθÌ˚ÏË. çÂÍÓÚÓ-
˚ „‡Ù˚ ÔÓÎÛ˜ËÎË ÒÔˆˇθÌ˚ ̇Á‚‡ÌËfl, Óڇʇ˛˘Ë Ëı
ÒÚÛÍÚÛÛ. ➤
ÅÂÁ·ÂÌ˚È „‡Ù N
n
= (V, ∅) ̇Á˚‚‡ÂÚÒfl „Û‰ÓÈ. éÌ ÒÓ-
ÒÚÓËÚ ËÁ n ËÁÓÎËÓ‚‡ÌÌ˚ı ‚¯ËÌ. çÂÓËÂÌÚËÓ‚‡ÌÌ˚È „‡Ù
Ò ˜ËÒÎÓÏ ‚¯ËÌ n Ë Â·Â m ̇Á˚‚‡ÂÚÒfl „‡ÙÓÏ ÚËÔ‡ (n, m).
óÚÓ·˚ ÔÓ‰˜ÂÍÌÛÚ¸ ÓÚÌÂÒÂÌÌÓÒÚ¸ ˝ÚËı ˜ËÒÂÎ Í „‡ÙÛ G(V, R),
ÔËÏÂÌfl˛Ú Ó·ÓÁ̇˜ÂÌËfl n = n(G) Ë m = m(G).
çÂÓËÂÌÚËÓ‚‡ÌÌ˚È „‡Ù Ò n ‚¯Ë̇ÏË, ͇ʉ‡fl ËÁ ÍÓÚÓ-
˚ı Ò‚flÁ‡Ì‡ ÒÓ ‚ÒÂÏË ÓÒڇθÌ˚ÏË ‚¯Ë̇ÏË „‡Ù‡, Ó·ÓÁ̇-
˜‡˛Ú K
n
Ë Ì‡Á˚‚‡˛Ú n-ÍÎËÍÓÈ. óËÒÎÓ Â·Â n-ÍÎËÍË m(K
n
) ‡‚-
ÌÓ
nn()
.
− 1
2
ɇ٠G
1
̇ ËÒ. 2.3 ÒÓÒÚÓËÚ ËÁ ÚÂı ÍÎËÍ: K
1
,
K
2
,
K
3
.
à
á·
êàë. 2.5
êàë. 2.6 êàë. 2.7

43
éËÂÌÚËÓ‚‡ÌÌ˚Ï Â·ÓÏ
r
r
(v
i
, v
j
) ÏÂÊ‰Û ‚¯Ë̇ÏË
„‡Ù‡ v
i
Ë v
j
·Û‰ÂÏ Ì‡Á˚‚‡Ú¸ ÒÚÂÎÍÛ, ‚ ˚ ı Ó ‰ fl ˘ Û ˛ ËÁ ‚Â-
¯ËÌ˚ v
i
Ë ‚ ı Ó ‰ fl ˘ Û ˛ ‚ ‚¯ËÌÛ v
j
(ËÒ. 2.6). ǯË̇ v
i
‰Îfl ÓËÂÌÚËÓ‚‡ÌÌÓ„Ó Â·‡
r
r
(v
i
, v
j
) ̇Á˚‚‡ÂÚÒfl ̇˜‡Î¸ÌÓÈ, ‡
‚¯Ë̇ v
j
– ÍÓ̘ÌÓÈ. äÓÏ ÚÓ„Ó, ‚¯Ë̇ v
j
̇Á˚‚‡ÂÚÒfl
ÒÓÒ‰ÌÂÈ ÔÓ ÓÚÌÓ¯ÂÌ˲ Í ‚¯ËÌ v
i
.
ɇÙ, Ëϲ˘ËÈ ÓËÂÌÚËÓ‚‡ÌÌ˚ · ‡, ·Û‰ÂÏ Ì‡Á˚‚‡Ú¸
ÓËÂÌÚËÓ‚‡ÌÌ˚Ï „‡ÙÓÏ Ë Ó·ÓÁ̇˜‡Ú¸
r
G(V, E).
è Ë Ï Â 4. ùÇå ÏÓÊÂÚ Ì‡ıÓ‰ËÚ¸Òfl ‚ ÚÂı ÒÓÒÚÓflÌËflı:
v
1
– ÓÊˉ‡ÂÚ ÂÏÓÌÚ‡; v
2
– ÌÂËÒÔ‡‚̇, ÓÊˉ‡ÂÚ ÂÏÓÌÚ‡; v
3
–
ÂÏÓÌÚËÛÂÚÒfl. 燘ÂÚËÚ¸ ÓËÂÌÚËÓ‚‡ÌÌ˚È „‡Ù ÒÓÒÚÓflÌËÈ
ùÇå.
ê  ¯ Â Ì Ë Â. éËÂÌÚËÓ‚‡ÌÌ˚È „‡Ù ÒÓÒÚÓflÌËÈ ùÇå ÔÓ͇-
Á‡Ì ̇ ËÒ. 2.7.
è Ë Ï Â 5. Ç Çñ ËϲÚÒfl ‰‚ ùÇå, ͇ʉ‡fl ËÁ ÍÓÚÓ˚ı
ÏÓÊÂÚ Ì‡ıÓ‰ËÚ¸Òfl ‚ ‰‚Ûı ÒÓÒÚÓflÌËflı: ËÒÔ‡‚̇ Ë ÌÂËÒÔ‡‚̇.
ëÓÒÚ‡‚ËÚ¸ ÓËÂÌÚËÓ‚‡ÌÌ˚ È „‡Ù ÒÓÒÚÓflÌËÈ Çñ. ➤
ÖÒÎË Û ‚ ¯ËÌ v
i
Ë v
j
ÂÒÚ¸ Â·Ó r (ÓËÂÌÚËÓ‚‡ÌÌÓ ËÎË
ÌÂÓËÂÌÚËÓ‚‡ÌÌÓÂ), ÚÓ „Ó‚ÓflÚ, ˜ÚÓ Â·Ó r Ë̈ˉÂÌÚÌÓ
‚¯ËÌ‡Ï v
i
Ë v
j
ËÎË Ì‡Ó·ÓÓÚ: ‚¯ËÌ˚ v
i
Ë v
j
Ë̈ˉÂÌÚÌ˚
Â·Û r. Ç ¯Ë̇ v
i
, Ì Ë̈ˉÂÌÚ̇fl ÌË͇ÍÓÏÛ Â·Û, ̇Á˚‚‡-
ÂÚÒfl ËÁÓÎËÓ‚‡ÌÌÓÈ.
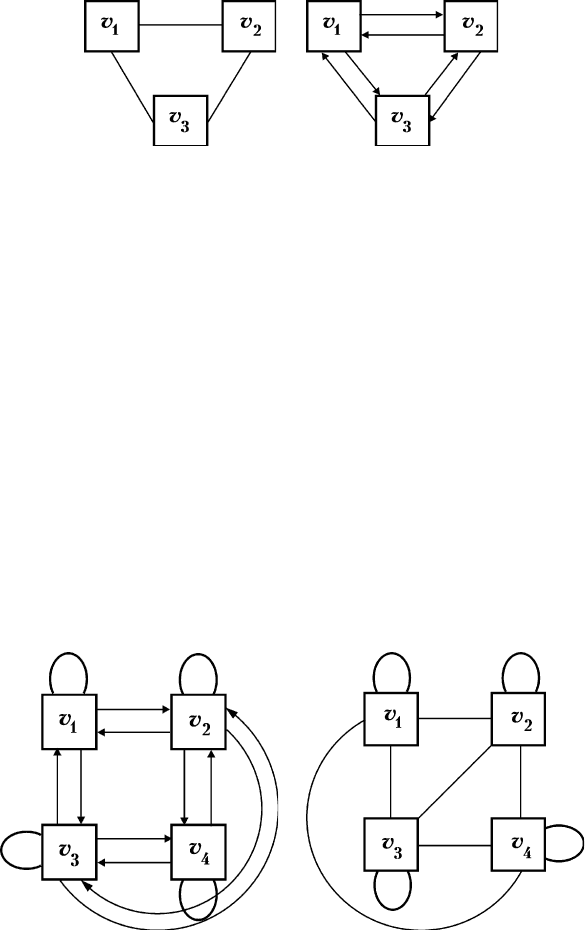
ɇÙ˚ (ÌÂÓËÂÌÚËÓ‚‡ÌÌ˚Â Ë ÓËÂÌÚËÓ‚‡ÌÌ˚ Â) ÏÓÊÌÓ
ËÁÓ·‡ÁËÚ¸ ‡Á΢Ì˚ÏË ˜ÂÚÂʇÏË. ç‡ÔËÏÂ, „‡Ù, ËÁÓ·‡-
ÊÂÌÌ˚È Ì‡ ËÒ. 2.7, ÏÓÊÌÓ ËÁÓ·‡ÁËÚ¸ Ú‡Í, Í‡Í ÔÓ͇Á‡ÌÓ Ì‡
ËÒ. 2.8, ‡ Ë ·. é˜Â‚ˉÌÓ, ˜ÚÓ ‚Ò ˝ÚË „‡Ù˚ Óڇʇ˛Ú Ó‰ÌÓ Ë
ÚÓ ÊÂ fl‚ÎÂÌËÂ.
ë‡Ï˚È ÔÓÒÚÓÈ „‡Ù ˝ÚÓ Ú‡ÍÓÈ, Û ÍÓÚÓÓ„Ó ‚Ò n ‚¯ËÌ
ËÁÓÎËÓ‚‡Ì˚. Ç ˝ÚÓÏ ÒÎÛ˜‡Â Ò‡Ï „‡Ù ̇Á˚‚‡ÂÚÒfl ÌÛ脇ÙÓÏ,
à
êàë. 2.8
êàë. 2.9
44
ÔËÏ ڇÍÓ„Ó „‡Ù‡ ËÁÓ·‡ÊÂÌ Ì‡ ËÒ. 2.9. ì ÌÛθ„‡Ù‡ ÌË
Ӊ̇ ËÁ ‚¯ËÌ Ì fl‚ÎflÂÚÒfl ÒÓÒ‰ÌÂÈ.
èÓÚË‚ÓÔÓÎÓÊÌÓÒÚ¸˛ ÌÛθ„‡Ù‡ fl‚ÎflÂÚÒfl „‡Ù, „‰Â ‚ÒÂ
‚¯ËÌ˚ ÒÓÒ‰ÌËÂ Ë ÌË Û Ó‰ÌÓÈ ‚¯ËÌ˚ ÌÂÚ ÔÂÚÂθ; Ú‡ÍÓÈ
„‡Ù ̇Á˚‚‡ÂÚÒfl ÔÓÎÌ˚ Ï (n-ÍÎËÍÓÈ).
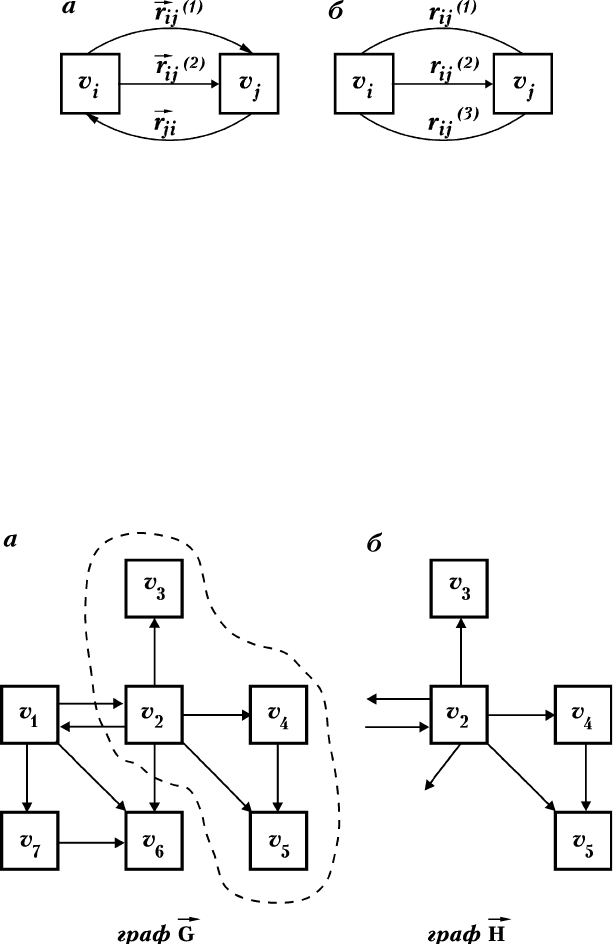
ÖÒÎË ‡ÒÒχÚË‚‡Ú¸ ÌÂÓËÂÌÚËÓ‚‡ÌÌ˚È „‡Ù, ÚÓ ÔË Ì‡-
΢ËË ÚÂı ‚¯ËÌ ÔÓÎÌ˚È „‡Ù ËÏÂÂÚ ‚ˉ, ÔÓ͇Á‡ÌÌ˚È Ì‡
ËÒ. 2.10. éËÂÌÚËÓ‚‡ÌÌ˚È ÔÓÎÌ˚È „‡Ù, ÒÓÒÚÓfl˘ËÈ ËÁ ÚÂı
‚¯ËÌ, ËÏÂÂÚ ‚ˉ, ÔÓ͇Á‡ÌÌ˚È Ì‡ ËÒ. 2.11. ì ÔÓÎÌÓ„Ó ÓËÂÌ-
ÚËÓ‚‡ÌÌÓ„Ó „‡Ù‡ β·Û˛ Ô‡Û ‚¯ËÌ v
i
Ë v
j
ÒÓ‰ËÌfl˛Ú ‰‚‡
·‡.
ç‡ÍÓ̈, ÏÓÊÌÓ ‡ÒÒÏÓÚÂÚ¸ „‡Ù, ‚Ò ‚¯ËÌ˚ ÍÓÚÓÓ„Ó
fl‚Îfl˛ÚÒfl ÒÓÒ‰ÌËÏË Ë ‚Ò ‚¯ËÌ˚ ËÏÂ˛Ú ÔÂÚÎË. í‡ÍÓÈ „‡Ù
·Û‰ÂÏ Ì‡Á˚‚‡Ú¸ ÔÓÎÌ˚Ï „‡ÙÓÏ Ò ÔÂÚÎflÏË. éÌ ÏÓÊÂÚ ·˚Ú¸
Í‡Í ÓËÂÌÚËÓ‚‡ÌÌ˚Ï (ËÒ. 2.12), Ú‡Í Ë ÌÂÓËÂÌÚËÓ‚‡ÌÌ˚Ï
(ËÒ. 2.13).
àÌÓ„‰‡, ÓÒÓ·ÂÌÌÓ ÔË ÒÓÒÚ‡‚ÎÂÌËË Ï‡¯ÛÚÓ‚ ‰‚ËÊÂÌËfl
Ú‡ÌÒÔÓÚ‡, ÔËıÓ‰ËÚÒfl ‡ÒÒχÚË‚‡Ú¸ ‰‚ ‚¯ËÌ˚ v
i
Ë v
j
,
ÒÓ‰ËÌÂÌÌ˚ Ì ӉÌËÏ Â·ÓÏ, ‡ ÌÂÒÍÓθÍËÏË (Í‡Í ÓËÂÌÚËÓ-
êàë. 2.10 êàë. 2.11
êàë. 2.12 êàë. 2.13
45
‚‡ÌÌ˚ÏË, Ú‡Í Ë ÌÂÓËÂÌÚËÓ‚‡ÌÌ˚ ÏË). ç‡ ËÒ. 2.11 ËÁÓ·‡ÊÂ-
Ì˚ Ú‡ÍË ÏÛθÚË„‡Ù˚ Ò Ó·ÓÁ̇˜ÂÌËflÏË Â·Â.
ÅÛ‰ÂÏ Ì‡Á˚‚‡Ú¸ „‡Ù ÍÓ̘Ì˚Ï, ÂÒÎË ÓÌ ËÏÂÂÚ ÍÓ̘ÌÓÂ
˜ËÒÎÓ ‚¯ËÌ. Ç ÔÓÚË‚ÌÓÏ ÒÎÛ˜‡Â, ÍÓ„‰‡ ˜ËÒÎÓ ‚¯ËÌ „‡Ù‡
·ÂÒÍÓ̘ÌÓ (ÌÓ Ò˜ÂÚÌÓÂ), „‡Ù ·Û‰ÂÏ Ì‡Á˚‚‡Ú¸ ·ÂÒÍÓ̘Ì˚Ï.
ɇ٠ç ̇Á˚‚‡ÂÚÒfl ˜‡ÒÚ¸˛ „‡Ù‡ G(H ⊂ G), ÂÒÎË ÏÌÓÊÂ-
ÒÚ‚Ó ‚¯ËÌ ˝ÚÓÈ ˜‡ÒÚË „‡Ù‡ V(H) ÔË̇‰ÎÂÊËÚ ÏÌÓÊÂÒÚ‚Û
‚¯ËÌ ‚ÒÂ„Ó „‡Ù‡ V(G) (V(H) ⊂ V(G)), ‡ ‚Ò ·‡ „‡Ù‡
ç fl‚Îfl˛ÚÒfl ·‡ÏË „‡Ù‡ G: R(ç) ⊆ R(G).
ç‡ ËÒ. 2.15, ‡ ËÁÓ·‡ÊÂÌ ÓËÂÌÚËÓ‚‡ÌÌ˚È „‡Ù
r
G, ‡ ̇
ËÒ. 2.15, · – Â„Ó ˜‡ÒÚ¸
r
H, ÔË ˝ÚÓÏ V(H) = {v
2
, v
3
, v
4
, v
5
}.
Ç ˝ÚÓÈ ÍÌË„Â Ë ‚ ·Óθ¯ËÌÒÚ‚Â ÔËÎÓÊÂÌËÈ ÔË ÒÓÒÚ‡‚ÎÂ-
ÌËË Ï‡ÚÂχÚ˘ÂÒÍËı ÏÓ‰ÂÎÂÈ ËÌÙÓχˆËÓÌÌ˚ı ÔÓˆÂÒÒÓ‚ Ë
êàë. 2.14
êàë. 2.15
46
ÛÔ‡‚ÎÂÌËfl Ì‡Ò ·Û‰ÛÚ ËÌÚ ÂÒÓ‚‡Ú¸ Ô Ó ‰ „ ‡ Ù ˚ . èÛÒÚ¸ V
1
ÂÒÚ¸
ÔÓ‰ÏÌÓÊÂÒÚ‚Ó ‚¯ËÌ V „‡Ù‡
r
G . íÓ„‰‡ ÔÓ‰„‡ÙÓÏ
r
G
1
(V
1
,
R
1
) „‡Ù‡
r
G(V, R) ·Û‰ÂÏ Ì‡Á˚‚‡Ú¸ ÔÓ‰ÏÌÓÊÂÒÚ‚Ó ‚ÒÂı ‚Â-
¯ËÌ „‡Ù‡ V
1
Ë ÏÌÓÊÂÒÚ‚Ó R
1
⊂ R Ú‡ÍËı · ËÁ „‡Ù‡
r
G,
Ó·‡ ÍÓ̈‡ ÍÓÚÓ˚ı ÔË̇‰ÎÂÊ‡Ú ÔÓ‰ÏÌÓÊÂÒÚ‚Û ‚¯ËÌ V
1
. ç‡
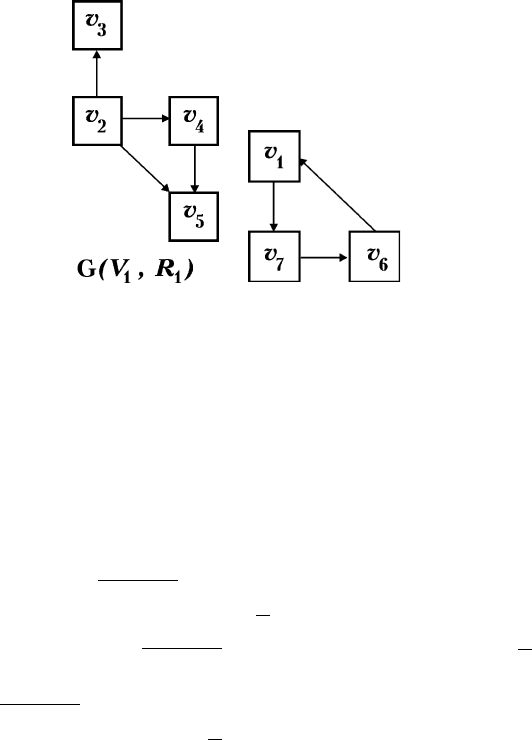
ËÒ. 2.16 ̇˜Â˜ÂÌ ÔÓ‰„‡Ù
r
G
1
(V
1
, R
1
) „‡Ù‡
r
G(R, V), ËÁÓ·-
‡ÊÂÌÌÓ„Ó Ì‡ ËÒ. 2.15, ‡, ÔË ÛÒÎÓ‚ËË, ˜ÚÓ ÔÓ‰ÏÌÓÊÂÒÚ‚Ó
‚¯ËÌ V
1
= {v
2
, v
3
, v
4
, v
5
}.
ÑÓÔÓÎÌÂÌËÂÏ ÔÓ‰„‡Ù‡
r
G(V
1
, R
1
) ‚ „‡Ù G(V, R) ̇Á˚-
‚‡ÂÚÒfl ÔÓ‰„‡Ù
r
G( VR,),
1
‚¯ËÌ˚ ÍÓÚÓÓ„Ó ÒÓÒÚ‡‚Îfl˛Ú ‰Ó-
ÔÓÎÌÂÌË ÔÓ‰ÏÌÓÊÂÒÚ‚‡ ‚¯ËÌ:
V
1
= V – V
1
, ‡ Ó·‡ ÍÓ̈‡ Â-
·Â ˝ÚÓ„Ó ÔÓ‰„‡Ù‡
r
G( VR,)
1
ÔË̇‰ÎÂÊ‡Ú ‰ÓÔÓÎÌÂÌ˲
V
1
ÔÓ‰ÏÌÓÊÂÒÚ‚‡ V
1
. ç‡ ËÒ. 2.17 ËÁÓ·‡ÊÂÌÓ ‰ÓÔÓÎÌÂÌË ÔÓ‰-
„‡Ù‡
r
G( VR,)
1
ÔË ÛÒÎÓ‚ËË, ˜ÚÓ ‚ÂÒ¸ „‡Ù ËÁÓ·‡ÊÂÌ Ì‡
ËÒ. 2.15, ‡ Ë ÔÓ‰ÏÌÓÊÂÒÚ‚Ó
V
1
= V – V
1
= {v
1
, v
6
, v
7
}.
ÅÛ‰ÂÏ „Ó‚ÓËÚ¸, ˜ÚÓ ‰‚‡ ÔÓ‰„‡Ù‡
r
G(V
1
, R
1
) Ë
r
G(V
2
, R
2
)
Ì ÔÂÂÒÂ͇˛ÚÒfl, ÂÒÎË Û ÌËı ÌÂÚ Ó·˘Ëı ‚¯ËÌ. ÑÛ„ËÏË
ÒÎÓ‚‡ÏË, ‰‚‡ ÔÓ‰„‡Ù‡
r
G(V
1
, R
1
) Ë
r
G(V
2
, R
2
) Ì ÔÂÂÒÂ͇-
˛ÚÒfl, ÂÒÎË ÔÂÂÒ˜ÂÌË (ÔÓËÁ‚‰ÂÌËÂ) ÔÓ‰ÏÌÓÊÂÒÚ‚‡ ‚¯ËÌ
V
1
Ë V
2
fl‚ÎflÂÚÒfl ÔÛÒÚ˚Ï:
V
1
⋅V
2
= V
1
∩ V
2
= ∅. (2.3)
èÓ‰„‡Ù˚
r
G(V
1
, R
1
) Ë
r
G( vR
22
,) „‡Ù‡
r
G(V, R) (ÒÏ. ËÒ.
êàë. 2.16 êàë. 2.17
47
2.15,
‡) Ì ÔÂÂÒÂ͇˛ÚÒfl, ÂÒÎË
V
1
= {v
1
,
v
6
,
v
7
};
V
2
= {v
2
,
v
3
,
v
4
,
v
5
}.
éÍÂÒÚÌÓÒÚ¸
r
G(v) ‚¯ËÌ˚ v ‚ „‡ÙÂ
r
G fl‚Îfl˛ÚÒfl ÔÓ‰-
ÏÌÓÊÂÒÚ‚ÓÏ ‚¯ËÌ „‡Ù‡
r
G, ÒÓ‰Âʇ˘Ëı ‚¯ËÌÛ v Ë ‚ÒÂ
ÒÓÒ‰ÌËÂ Ò ÌÂÈ ‚¯ËÌ˚.
éÔ‡ˆËË Ì‡‰ „‡Ù‡ÏË. èÓ‰„‡Ù
G, ‰ÓÔÓÎÌfl˛˘ËÈ „‡Ù G
‰Ó n-ÍÎËÍË K
n
, ̇Á˚‚‡ÂÚÒfl ‰ÓÔÓÎÌËÚÂθÌ˚Ï „‡ÙÓÏ ‰Îfl G. Ç
ÔÓ‰„‡Ù
G ‚ıÓ‰flÚ ÚÂ Ë ÚÓθÍÓ Ú ·‡ K
n
, ÍÓÚÓ˚ Ì ‚ıÓ‰flÚ
‚ „‡Ù G.
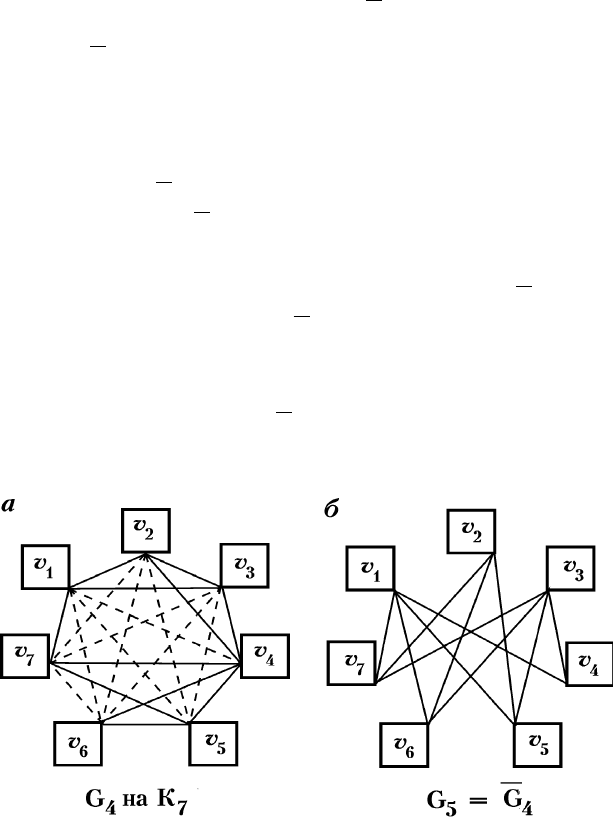
è Ë Ï Â 6. ç‡ ËÒ. 2.18, ‡ ËÁÓ·‡ÊÂ̇ 7-ÍÎË͇, ‚ ÍÓÚÓÓÈ
ÊËÌ˚ÏË ÎËÌËflÏË ‚˚‰ÂÎÂÌ „‡Ù G
4
ÚËÔ‡ (7,10), ‚Íβ˜‡˛˘ËÈ
·‡ r(1, 2), r(1, 3), r(2, 4), r(4, 5), r(4, 6), r(4, 7), r(5, 6),
r(5, 7), r(6, 7) (Á‰ÂÒ¸ ˆËÙ˚ ‚ ÒÍӷ͇ı – ÌÓχ ‚¯ËÌ).
èÓ‰„‡Ù G
5
=
G
4
ÔÓÎÛ˜‡ÂÚÒfl ËÁ ÍÎËÍË K
7
Û‰‡ÎÂÌËÂÏ Â·Â
ÔÓ‰„‡Ù‡ G
4
. ɇÙ
G
4
ËÁÓ·‡ÊÂÌ Ì‡ ËÒ. 2.18, ·. éÌ ‚Íβ˜‡ÂÚ
·‡, ÍÓÚÓ˚ÏË Í‡Ê‰‡fl ‚¯Ë̇ ËÁ {1, 2, 3} ÒÓ‰ËÌÂ̇ Ò Í‡Ê-
‰ÓÈ ‚¯ËÌÓÈ ËÁ {4, 5, 6, 7}, Ë ËÏÂÂÚ ÚËÔ (7.11). ÑÎfl Ô Ó‚ÂÍË
Ô‡‚ËθÌÓÒÚË Ì‡ıÓʉÂÌËfl Â·Â Ô Ë ÔÓÒÚÓÂÌËË
G
4
ÏÓÊÌÓ
ËÒÔÓθÁÓ‚‡Ú¸ ÒÓÓÚÌÓ¯ÂÌË m
(G
4
) + m(G
4
) = m(K
7
) = 7⋅6/2 =
= 21. á‡ÏÂÚËÏ, ˜ÚÓ „‡Ù G
5
‰‚Û‰ÓθÌ˚È. é‰ÌÛ ‰Óβ ÒÓÒÚ‡‚ÎflÂÚ
ÏÌÓÊÂÒÚ‚Ó ‚¯ËÌ V
1
= {1, 2, 3}, ‡ ‰Û„Û˛ – V
2
= {4, 5, 6, 7}, Ë
ÔË ˝ÚÓÏ Í‡Ê‰‡fl ‚ ¯Ë̇ V
1
ÒÓ‰ËÌÂ̇ Ò Í‡Ê‰ÓÈ ‚¯ËÌÓÈ
V
2
. í‡ÍËÏ Ó·‡ÁÓÏ, G
5
=
G
4
ÂÒÚ¸ ÔÓÎ̇fl ‰‚Û‰Óθ̇fl ÍÎË-
͇ K
3,4
. ➤
êàë. 2.18
