Naber G.L. The Geometry of Minkowski Spacetime. An Introduction to the Mathematics of the Special Theory of Relativity

Подождите немного. Документ загружается.

274 4 Prologue and Epilogue: The de Sitter Universe

will be denoted I

−

and called past null inﬁnity of M, while those satisfying

= π

are denoted I

and called future null inﬁnity of M. The intersection of

these two is just the point (t

)=(0,π) which is denoted i

◦

and called

space-like inﬁnity of M.

Note: One should observe that the boundary points i

−

, I

−

, I

and i

◦

we have just isolated are precisely the points at which the conformal factor

Ωgivenby(4.5.18)vanishes.

visualize I

−

and I

using the same device employed for the conformal

embedding of dS in E. Unfolding the 2-dimensional Einstein cylinder onto

the

-plane, the equations t

−

= −π and t

= π determine

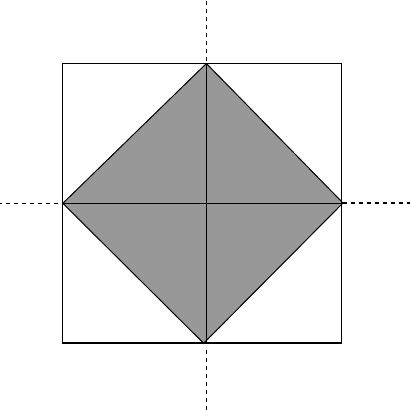
straight lines. This is depicted in Figure 4.5.7, but a bit of care is required

terpreting the picture. Since (

)=(π, 0) and (

)=(−π, 0)

come from the same point on the cylinder we have identiﬁed them and drawn

both of the straight lines twice on opposite sides of the t

-axis. When the

plane is folded back up into the cylinder these become the curves labeled I

−

and I

in Figure 4.5.8.

− π

+ f

= π

−

+ f

= π

−

− f

= − π

−

− f

= − π

−

Fig. 4.5.7

The justiﬁcation for the names we have attached to the various components

of the conformal boundary of M is arrived at by examining the images in E

of geodesics in M. We begin with future-directed null geodesics in M.We

have shown already that these map to (reparametrizations of) null geodesics

4.5 Inﬁnity in Minkowski and de Sitter Spacetimes 275

−

= 0

−

−π

−

Fig. 4.5.8

in E, but our interest now is in where they begin and end. To simplify the

arithmetic we will consider geodesics that pass through the origin of M, but

the same conclusions follow for those that do not. Thus, we consider a curve

α : R →Mgiven by

α(s)=s(v

)

where (v

)

+(v

)

+(v

)

− (v

)

=0andv

> 0. Then, on α, ρ

(sv

)

+(sv

)

+(sv

)

=(sv

)

so, for s ≥ 0,ρ= v

s.Butρ

− t

then gives t = v

s as well so (ρ, t)=(v

s, v

s). In particular, t − ρ =0

and t + ρ =2v

s →∞as s →∞.Thus,w =0andv →∞so q =0and

p →

as s →∞.Consequently,t



→

and ρ



→

and so the image of the

null geodesic under the conformal embedding F of M into E (Exercise 4.5.9)

satisﬁes

→ π

276 4 Prologue and Epilogue: The de Sitter Universe

and so approaches I

. In the same way the image of α approaches I

−

s →−∞. Although I

−

and I

do not lie in M one thinks of future-directed

null geodesics as beginning on I

−

and ending on I

A future-directed timelike geodesic through the origin in M is a curve

α : R →Mthat can be written in the form

α(s)=s(v

)

where (v

)

+(v

)

+(v

)

−(v

)

= −1andv

> 0. The image of α under the

conformal embedding of M into E need not be a geodesic, but it is a timelike

curve which we now ask the reader to show must begin on i

−

and i

Exercise 4.5.10 Show that the image in E of the future-directed timelike

geodesic α approaches i

−

as s →∞and i

as s →∞.

A spacelike geodesic α : R →Min M canbewrittenasα(s)=

s(v

), where (v

)

+(v

)

+(v

)

−(v

)

= 1 and one can assume

without loss of generality that v

≥ 0. The image of α under the conformal

embedding of M into E need not be a geodesic, but it is a spacelike curve.

Exercise 4.5.11 Show that the image in E of the spacelike geodesic α ap-

proaches i

◦

as s →∞and also as s →−∞.

−

Fig. 4.5.9

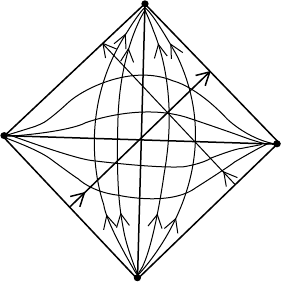
Figure 4.5.9 is just Figure 4.5.7 again with all of the various pieces of the con-

formal boundary of M identiﬁed by name and images in E of a few geodesics

of each type in M included. This is the Penrose diagram of Minkowski space-

time and, contrasted with the corresponding diagram for dS (Figure 4.5.5),

does mu

to elucidate the diﬀerences in causal structure between the two.

There are, for example, no particle or event horizons in M precisely because

timelike geodesics “focus” on i

−

and i

rather than I

−

and I

so that the

4.5 Inﬁnity in Minkowski and de Sitter Spacetimes 277

null cone at any point “catches” all of the timelike worldlines. This technique

has been used to great eﬀect in general relativity, but it goes much further

than this. Penrose devised the technique to study the asymptotic behavior

of solutions to massless free-ﬁeld equations in spinor form such as those with

which we concluded Section 3.6. The behavior of interest is conformally in-

variant and so, rather than employing complicated limiting procedures, one

can analyze the behavior at points of I

−

and I

using the more familiar

local techniques of geometry and analysis. This is quite another story, how-

ever, and the best service we can provide for those interested in pursuing the

matter is to send them from here to [Pen

Appendix A

Topologies For M

A.1 The Euclidean Topology

In this appendix we wish to lay before the reader certain material which

requires a bit more in the way of background than the text itself and which

admittedly has not had a profound impact on subsequent research in rela-

tivity, but which is nonetheless remarkable from both the physical and the

mathematical points of view. We will assume a very basic familiarity with

elementary point-set topology and adopt [Wi] as our canonical reference.

The subject we wish to address had its origins in the extraordinary paper

] of Zeeman in 1967. Zeeman observed that the ordinary Euclidean topol-

ogy for M (deﬁned below) has, from the relativistic viewpoint, no physical

signiﬁcance or justiﬁcation and proposed an alternative he called the “ﬁne”

topology. This topology was easy to describe, physically well motivated and

had the remarkable property that its homeomorphism group (also deﬁned

below) was essentially just the Lorentz group (together with translations and

nonzero scalar multiplications). Thus, perhaps the most important group in

all of physics is seen to emerge at the very primitive level of topology, i.e.,

from just an appropriate deﬁnition of “nearby” events. The ﬁne topology is,

however, from the technical point of view, rather diﬃcult to work with and

the arguments in [Z

] are by no means simple. In 1976, Hawking, King and

McCarthy [HKM] described another topology on M which seemed physi-

cally even more natural, had precisely the same homeomorphism group as

Zeeman’s ﬁne topology and required for the proof of this nothing beyond

the most rudimentary point-set topology and Zeeman’s Theorem 1.6.2. This

so-called “path topology” for M is the object of our investigations in this

appendix.

We begin by transferring to M the standard Euclidean topology of R

via a

linear isomorphism. Speciﬁcally, we select some ﬁxed admissible basis {e

}

a=1

for M (this determines an obvious linear isomorphism of M onto R

). If x =

and x

= x

are two points in M we deﬁne the E-distance from x

, : An Introduction

, Applied Mathematical Sciences 92,

G.L. Naber The Geometry of Minkowski Spacetime to the Mathematics

of the Special Theory of Relativity

DOI 10.1007/978-1-4419-7838-7, © Springer Science+Business Media, LLC 2012

279

280 A Topologies For M

x by d

,x)=





− x





− x





− x





− x





1/2

Then d

is a metric on M, i.e., satisﬁes (1) d

(x, x

)=d

,x), (2)

,x) ≥ 0andd

,x) = 0 if and only if x = x

,and(3)d

,x) ≤

,y)+d

(y, x) for all x

,xand y in M.Consequently,d

determines, in

the usual way (3.2 of [Wi]) a topology E for M called the Euclidean (or E-)

topology. Speciﬁcally, if x

is in M and ε>0 we deﬁne the E-open ball of

radius ε about x

)={x ∈M: d

,x) <ε}.

A subset V of M is then said to be E-open if for every x

in V there exists

an ε>0 such that N

) ⊆ V . The collection of all E-open sets in M con-

stitutes the E-topology for M. When thinking of M as being endowed with

the Euclidean topology we will denote it M

. E’s will likewise be appended

to various other terms and symbols to emphasize that we are operating in the

Euclidean topology, e.g., maps will be referred to as “E-continuous”, “Cl

A”

and “bdy

A” will designate the E-closure and E-boundary of A and so on.

is, of course, homeomorphic to R

with its customary Euclidean topology

so that its basic topological properties are well-known,

e.g.,itisﬁrstcount-

able, separable, locally compact, but not compact, pathwise connected, etc.

Notice that the deﬁnition of the E-metric d

on M is not invariant under

Lorentz transformations. That is, if d

,x) is computed by the deﬁning

formula from the coordinates of x

and x relative to another admissible basis

{ˆe

} for M the result will, in general, be diﬀerent. The reason for this is clear

since the two bases are related by an element of L and elements of L preserve

the Lorentz inner product and not the Euclidean inner product (i.e., they

satisfy Λ

−1

= ηΛ

η rather than Λ

−1

=Λ

). Nevertheless, two such metrics,

while not equal, are equivalent in the sense that they determine the same

topology for M (because an element of L is a one-to-one linear map of M

onto M and so an E-homeomorphism).

A.2 E-Continuous Timelike Curves

In Section 1.4 we deﬁned what it meant for a smooth curve in M to be

“timelike” and “future- (or past-) directed”. For the deﬁnition of the topology

we propose to describe in the next section it is essential to extend these

notions to the class of curves in M that are E-continuous, but need not

have a velocity vector at each point. Thus, we let I denote a (nondegenerate)

interval in R (open, closed, or half-open) and consider a curve α : I →M

that is E-continuous (i.e., α

−1

(V )isopeninI for every E-open set V in M).

Its not-so-basic topological properties are quite another matter, however. Indeed, in many

topological ways,

is unique among the Euclidean spaces R

(see, for example, [FL]).

A.2 E-Continuous Timelike Curves 281

Fix a t

in I.Wesaythatα is future-timelike at t

if there exists a connected,

relatively open subset U of I containing t

such that

t ∈ U and t<t

=⇒ α(t)  α(t

)

and

t ∈ U and t

<t=⇒ α(t

)  α(t).

(U is an interval which may contain one or both of the endpoints of I,ifI

happens to have endpoints). Past-timelike at t

is deﬁned similarly. α is said

to be future-timelike (resp., past-timelike) if it is future-timelike (resp., past-

timelike) at every t

in I. Finally, α is timelike if it is either future-timelike

or past-timelike.

Any curve α : I →Mthat is smooth has component functions rel-

ative to any admissible basis that are continuous as maps from I into R.

Since M

is homeomorphic to R

with its product topology, such an α is

E-continuous (8.8 of [Wi]). According to Lemma 1.4.7, a smooth curve that

is timelike and future-directed in the sense of Section 1.4 is therefore also

future-timelike in our new sense. Of course, the same is true of smooth, time-

like and past-directed curves. However, any timelike polygon (which has no

velocity vector at its “joints”) can obviously be parametrized so as to become

either future-timelike or past-timelike, but is not “smooth-timelike”. Oddly

enough, an E-continuous curve can be timelike and smooth without being

smooth-timelike in the sense of Section 1.4. For example, if {e

} is an ad-

missible basis and if one deﬁnes α : R →Mby α(t)=(sint)e

+ te

,then

α is future-timelike and smooth, but α



(t)=(cost)e

+ e

which is null at

t = nπ, n =0, ±1, ±2, ... (see Figure A.2.1). This is unfortunate since

it complicates the physical interpretation of “E-continuous future-timelike”

somewhat. One would like to regard such a curve as the worldline of a mate-

rial particle which may be undergoing abrupt changes in speed and direction

(due, say, to collisions). Of course, having a null velocity vector at some point

would tend to indicate a particle momentarily attaining the speed of light and

this we prefer not to admit as a realistic possibility. One would seem forced

to accept a curve of the type just described as an acceptable model for the

worldline of a material particle only on the intervals between points at which

the tangent is null (notice that the situation cannot get much worse, i.e.,

the velocity vector of a smooth future-timelike curve cannot be null on an

interval, nor can it ever be spacelike).

We proceed now to derive a sequence of results that will be needed in the

next section.

Lemma A.2.1 Let {e

}

a=1

be an admissible basis for M and α : I →

M an E-continuous timelike curve. If α is future-timelike, then x

(α(t)) is

increasing on I. If α is past-timelike, then x

(α(t)) is decreasing on I. In

particular, if α is timelike, it is one-to-one.

282 A Topologies For M

Fig. A.2.1

Proof: Suppose α is future-timelike (the argument for α past-timelike is

similar). Let t

∈ I with t

. We show that x

(α(t

)) <x

(α(t

)).

Suppose, to the contrary, that x

(α(t

)) ≥ x

(α(t

)). x

(α(t)) is a real-valued

continuous (8.8 of [Wi]) function on the closed bounded interval [t

]and

so achieves a maximum value at some t

∈ [t

]. Since α is future-timelike

at t

and p  q implies x

(p) <x

(q),x

(α(t)) must increase immediately

to the right of t

so t

.Butx

(α(t

)) >x

(α(t

)) ≥ x

(α(t

)) implies

so t

∈ (t

). But α is future-timelike at t

and so x

(α(t)) must

increase immediately to the right of t

and this contradicts the fact that, on

],x

(α(t)) has a maximum at t

. 

Next we show that Theorem 1.4.6 remains true if “smooth future-directed

timelike” is replaced with “E-continuous future-timelike”.

Theorem A.2.2 LetpandqbetwopointsinM.Thenp  q if and only

if there exists an E-continuous future-timelike curve α :[a, b] →Msuch that

α(a)=p and α(b)=q.

Proof: The necessity is clear from Theorem 1.4.6. For the suﬃciency we

assume α :[a, b] →Mis E-continuous future-timelike with α(a)=p and

α(b)=q.Foreacht in [a, b] we select a connected, relatively open subset

of [a, b] containing t as in the deﬁnition of future-timelike at t.Then

: t ∈ [a, b]} is an open cover of [a, b] so, by compactness (17.9 of [Wi]),

we may select a ﬁnite subcover U = {U

,..., U

A.2 E-Continuous Timelike Curves 283

By deﬁnition, a ∈ U

.Moreover,ifb ∈ U

,thenα(a)  α(b)andweare

done. If b/∈ U

, then the right-hand endpoint s

of U

is less than or equal

to b and not in U

Select a U

in U such that s

∈ U

.ThenU

= U

, but U

∩ U

= ∅.

Select a T

∈ U

∩ U

such that a<T

.Now,ifb ∈ U

,thenα(a) 

α(T

)  α(t

)  α(b) and we are done. Otherwise, the right-hand endpoint

of U

is less than b and not in U

. Repeat the process, beginning at T

rather than a. Select a U

in U with s

∈ U

.ObservethatU

= U

and

= U

since s

is in neither U

nor U

. However, U

∩U

= ∅. Select T

as above and continue to repeat the process. Since U is ﬁnite and covers [a, b]

the procedure must terminate in a ﬁnite number of steps with α(a)  α(b)

as required. 

Next we prove that an E-continuous curve that is timelike at each point

in an interval must have the same causal character (future-timelike or past-

timelike) at each point. In fact, we prove more.

Lemma A.2.3 Let α : I →Mbe an E-continuous curve. If α is timelike

at each t

in the interior Int I of I, then α is timelike.

Proof: We ﬁrst show that α is either future-timelike at each t

∈ Int I or

past-timelike at each t

∈ Int I. The procedure will be to show that the set

S = {t

∈ Int I : α is future-timelike at t

} is both open and closed in Int

I and so, since Int I is connected, is either ∅ or all of Int I (26.1 of [Wi]).

Suppose then that S = ∅.Lett

∈ S and select some U ⊆ Int I as in the

deﬁnition of “future-timelike at t

”. We show that α is future-timelike at

each t in U so t

∈ U ⊆ S and, since t

∈ S was arbitrary, conclude that S

is open. First suppose there were a t

in U at which α is past-timelike.

Exercise A.2.1 Relative to an admissible basis consider x

(α(t)) on [t

]

and argue as in the proof of Lemma A.2.1 to derive a contradiction.

A similar argument shows that there can be no t

in U at which α is

past-timelike. Thus, U ⊆ S as required so S is open. The same argument

shows that {t

∈ Int I : α is past-timelike at t

}, which is the complement of

S in Int I,isopeninIntI so S is open and closed in Int I as required. Thus,

either S = ∅ or S =IntI so α is either past-timelike at every t

∈ Int I or

future-timelike at every t

∈ Int I.

Now we show that if I has endpoints then α must be timelike and have the

same causal character at these points that it has on Int I. The arguments are