Naber G.L. The Geometry of Minkowski Spacetime. An Introduction to the Mathematics of the Special Theory of Relativity

Подождите немного. Документ загружается.

254 4 Prologue and Epilogue: The de Sitter Universe

dψ

+sin

ψ(dφ

+sin

φdθ

)(Σ=S

)

dψ

+ ψ

(dφ

+sin

φdθ

)(Σ=R

)

dψ

+sinh

ψ(dφ

+sin

φdθ

)(Σ=H

(1))

Each of our free observers has a worldline that intersects Σ at, without loss

of generality, t = 0. Now “move” the coordinates of Σ along these worldlines

by ﬁxing each observer’s spatial coordinates ψ, φ, θ at the values they have

at t = 0 on Σ and taking the fourth coordinate of each event to be the proper

time t of the observer that experiences that event. Allowing the “scale” of the

spatial cross sections to (perhaps) vary with t and recalling that the observer

worldlines are orthogonal to these cross sections we conclude that, in these

coordinates, the line element of M should have one of the forms

−dt

+ a

(t)

⎧

⎪

⎨

⎪

⎩

dψ

+sin

ψ(dφ

+sin

φdθ

)

dψ

+ ψ

(dφ

+sin

φdθ

)

dψ

+sinh

ψ(dφ

+sin

φdθ

)

where a(t) is some positive function of t. These are called Robertson-Walker

metrics and our conclusion (or, rather, now our ansatz) is that a spatially

homogeneous and isotropic spacetime should admit coordinate systems in

which the spacetime metric g assumes one of these forms.

If we were in the business of doing cosmology (which we are not) we

would choose one of these, substitute into the Einstein equations (for some

choice of Λ and some T

) and determine the scale function a(t). Our inter-

est in the Robertson-Walker metrics is that we have seen them all before

andallinthesameplace.Indeed,exceptforthenamesofthevariables,

themetricfordS in global coordinates given by (4.3.22) is the Robertson-

lker

metric with spherical spatial cross sections and a(t)=cosht;in

planar coordinates, Exercise 4.3.19 gives the same metric as a Robertson-

lker

metric with ﬂat spatial cross sections and a(t)=e

; in hyperbolic

coordinates, Exercise 4.3.20 exhibits the metric of dS as a

Rob

ertson-

Walker metric with spatial cross sections that are hyperbolic 3-spaces and

a(t)=sinht. These three represent very diﬀerent physical situations, of

course, but they are all simply diﬀerent descriptions of the same underlying

spacetime (or a part of it).

It is certainly interesting, but perhaps not so terribly surprising that

entirely diﬀerent physical pictures of the universe can be modeled in a sin-

gle spacetime. Certain things about a spacetime manifold are “absolute”,

i.e., independent of observer. The geodesics, for example, and the Riemann

curvature tensor, as well as the causality relations between events are all de-

termined entirely by the manifold and its metric. However, a spacetime such

as dS admits many families of timelike geodesics ﬁlling the manifold (e.g., the

−,t

−,andt

–coordinate curves), each with as much right as the other to

claim for itself the title of “cosmic observer” and determine its own “instan-

taneous 3-spaces.” This is entirely analogous to the situation in Minkowski

4.5 Inﬁnity in Minkowski and de Sitter Spacetimes 255

spacetime where diﬀerent admissible observers disagree as to which sets of

events count as instantaneous 3-spaces (although in this case they all agree

that “space” is R

Perhaps more interesting is the fact that all of these various observers agree

that they are in an empty universe (Exercise 4.4.1), not unlike an admissible

serv

er in Minkowski spacetime, but they see the world quite diﬀerently

than their Minkowskian colleague. Aside from the fact that they may see

“space” as spherical or hyperbolic, they also see it as expanding (indeed,

expanding at an exponentially increasing rate) due to the presence of the

scale factors a(t)=cosht, e

, and sinh t. Any two observers in the family

of cosmic observers have ﬁxed spatial coordinates, but even so their spatial

separation is increasing exponentially with t (in the spherical case one might

picture a balloon being blown up). Remarkably enough, recent astronomical

observations suggest that the expansion of our universe is, indeed, accelerat-

ing and this has prompted a renewed interest in the de Sitter universe as a

potential alternative to Minkowski spacetime (see, for example, [CGK]). As

hav

e seen, these two models of the empty universe have quite diﬀerent

properties and we will conclude by describing yet one more such property,

this one related to the asymptotic behavior of worldlines.

4.5 Inﬁnity in Minkowski and de Sitter Spacetimes

We propose to oﬀer a precise deﬁnition of “inﬁnity” in both Minkowski and

de Sitter spacetimes and then show how the two diﬀer in the behavior of

their timelike and null curves “at inﬁnity.” This will lead to the notions of

particle and event “horizons” in dS that do not exist in M (since we are now

regarding Minkowski spacetime as a Lorentzian manifold it would probably

be more appropriate to call it R

3,1

, but we’ll stick with M). The idea behind

all of this is due to Roger Penrose and amounts to “squeezing” both M and dS

into ﬁnite regions of yet another spacetime in such a way that the boundaries

of these regions can be identiﬁed with “inﬁnity” in M and dS. The spacetime

into which we squeeze them is, moreover, of considerable signiﬁcance, at least

historically. It is called the Einstein static universe and we shall denote it E.

Remark: Here, very brieﬂy, is the story of E. As Einstein originally pro-

posed them, the ﬁeld equations did not contain a cosmological constant (they

were our (4.4.1) with Λ = 0). Einstein applied these equations to a spatially

homogeneous and isotropic universe with S

spatial cross sections and ﬁlled

with a uniform “dust” of galaxies (T

was the energy-momentum tensor for

what is called a perfect ﬂuid with zero pressure). He found, much to his cha-

grin, that the solution described an expanding universe. He was chagrined by

this because, at the time, there was no reason to believe that the universe

was anything but what it had been assumed for centuries to be, that is, ﬁxed

256 4 Prologue and Epilogue: The de Sitter Universe

and immutable. He then, very reluctantly, modiﬁed his ﬁeld equations by in-

cluding the cosmological term Λg

because he could then, for a very speciﬁc

choice of Λ, ﬁnd a static solution E. Then, of course, along came Edwin Hub-

ble who interpreted the observed redshift of light from distant galaxies as a

Doppler shift and concluded that the universe is, in fact, expanding. Einstein

(and almost everyone else) then abandoned E along with the cosmological

constant that gave rise to it. As we have seen however, there may be reason

to resurrect Λ and there are those who believe that E also deserves a reprieve

(see [DS]).

Our

ﬁrst t

ask t

hen is to construct the spacetime into which we will squeeze

M and dS.SinceE can be described in terms very much like those with which

we described dS we will leave some of the details to the reader. As a set, E

consists of those points (u

)inR

satisfying

)

+(u

)

+(u

)

+(u

)

and so is pictured as a cylinder setting on the 3-sphere in R

Exercise 4.5.1 Show that E is diﬀeomorphic to S

× R (and therefore

to dS ).

Now deﬁne a map from R

to R

=sin

cos

=sin

sin

cos

=sin

sin

θ (4.5.1)

=cos

= t

Exercise 4.5.2 Show that the image of the map (4.5.1)isallofE and th

each

point in E is contained in an open subset of E on which the inverse of

the map is a chart.

Thus, with the usual caveat regarding appropriate ranges for the variables,

(

θ, t

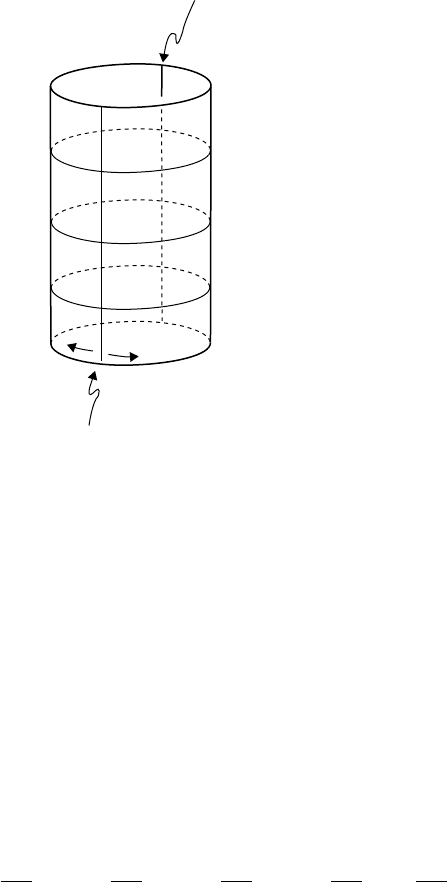
) are global coordinates on E.InFigure4.5.1 the cylinder E

is represented by suppressing the coordinates

and

θ and regarding

an angular coordinate on a copy of S

in S

(more precisely, Figure 4.5.1

represents a slice of E obtained by ho

lding

and

θ ﬁxed).

Exercise 4.5.3 Restrict the M

-inner product to each tangent space

(E),p∈E, and show that the corresponding line element in (

θ, t

coordinates is

= d

+sin



+sin



− dt

. (4.5.2)

Remark: The reader may wish to pause and compare (4.5.2) with the result

of Exercise 4.3.18.

will have more to say about this shortly. It should also

4.5 Inﬁnity in Minkowski and de Sitter Spacetimes 257

−

= 0 (S

)

Fig. 4.5.1

be clear from (4.5.2)whyE is called the Einstein “static” universe. The

spatial cross sections S

of constant t

all have the same geometry, given by

+sin



+sin



; there is no time-dependent scale factor such

as one sees in the Robertson-Walker metrics we have described for dS.

This completes the description of the spacetime E, but we will also need

some information about its geodesics. Rather than computing Christoﬀel

symbolsandtryingtosolve(4.3.27) we notice that, just as for dS,t

is a simple normal vector to each point of E with which we can pick out those

curves in E with α



tan

(t)=0 for each t.

Any smooth curve in E can be written α(t)=(u

(t),u

(t),

(t)), where (u

(t))

+(u

(t))

+(u

(t))

+(u

(t))

= 1. Diﬀerentiating with

respect to t gives

0=u

(t)

+ u

(t)

+ u

(t)

+ u

(t)

− 0 ·

which says that the M

-inner product of α



(t) with the projection of α(t)

into S

, i.e., with (u

(t),u

(t), 0), is zero. Thus, for any p =

) ∈E, the vector (p

, 0) in M

is orthogonal to

(E). We conclude that T

(E) can be viewed as the orthogonal complement

in M

of the vector (p

, 0). Moreover, a smooth curve α(t)inE

258 4 Prologue and Epilogue: The de Sitter Universe

is a geodesic of E if and only if its acceleration α



(t)=



,...,



is a multiple of (u

(t),..., u

(t), 0) for each t.Inparticular,u

must be a

linear function of t so a geodesic must be of the form

α(t)=(u

(t),u

(t), at + b) (4.5.3)

for some constants a and b. Moreover, the projection

(t)=(u

(t),u

(t)) (4.5.4)

of α into S

has the property that α



(t) is a multiple of α

(t)foreacht so,

by Exercise 4.3.24, α

is a geodesic of S

and therefore either a constant if

it is degenerate or a constant speed parametrization of a great circle in S

it is not.

Exercise 4.5.4 Let α be a nondegenerate geodesic of E written in the form

(4.5.3)andα

its projection into S

as in (4.5.4). Prove each of the following

(see Figure 4.5.2).

)

f a =0

henα is a constant speed parametrization of a great circle in

the 3-sphere at “height” u

= b and is spacelike.

(b) If α

(t) is degenerate (say, α

(t)=





for all t), then α

is a constant speed parametrization of a “vertical” straight line and is

timelike.

is not degenerate, then α is a “helix” sitting over some

great circle in S

and (α



(t),α



(t)) = (α



(t),α



(t)) − a

α is

⎧

⎪

⎨

⎪

⎩

null , if (α



(t),α



(t)) = a

timelike , if 0 < (α



(t),α



(t)) <a

spacelike , if (α



(t),α



(t)) >a

Notice that Figure 4.5.2 exhibits a feature of the Einstein static universe

that we

hav

e not encountered before. Two points can be joined by both a

timelike and a null geodesic (both future-directed if this is deﬁned, as for

dS, in terms of the relations  and < in M

). Notice also that, since any

linear reparametrization of a geodesic is also a geodesic, when a =0wemay

assume that it is 1 and b = 0. In particular, the null geodesics of E can all be

described as

α(t)=(α

(t),t),

where

(α



(t),α



(t)) = 1

for −∞ <t<∞ so that α

is a unit speed parametrization of a great circle

in S

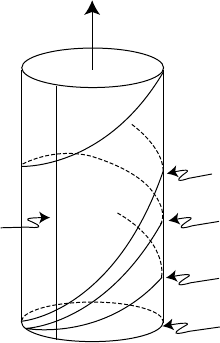
4.5 Inﬁnity in Minkowski and de Sitter Spacetimes 259

spacelike

timelike

spacelike

null

Fig. 4.5.2

The next order of business is to formulate a precise notion of what it means

to “squeeze” one manifold with metric into another. We have seen already

that if M

and M

are manifolds with metrics g

and g

, respectively, then

an isometry from M

to M

is a diﬀeomorphism F : M

→ M

that preserves

inner products at each point in the sense that

((F ◦ α)



), (F ◦ β)



)) = g

(α



),β



))

for all smooth curves α and β in M

with α(t

)=β(t

). If such an isometry

exists, then, in particular, M

and M

are the same as manifolds (diﬀeomor-

phic), but they are geometrically the same as well since F preserves lengths

of curves, carries geodesics to geodesics, and preserves the curvature; there is

no “squeezing” going on here. To achieve this we will relax the requirement

that F preserve inner products at each point and require only that these

inner products change by at most some positive multiple at each point. More

precisely, we deﬁne a conformal diﬀeomorphism from M

to M

to be a dif-

feomorphism F : M

→ M

with the property that, for each p ∈ M

and all

smooth curves α and β in M

with p = α(t

)=β(t

((F ◦ α)



), (F ◦ β)



)) = Ω

(p)g

(α



),β



))

for some smooth, positive function

Ω:M

→ R.

To facilitate the comparison of the two metrics and their geometries it is

often convenient to have them both live on the same manifold (or, rather,

260 4 Prologue and Epilogue: The de Sitter Universe

the same copy of the single manifold that both M

and M

are diﬀeomorphic

to). For this we deﬁne the pullback of g

to M

to be the metric F

∗

on M

deﬁned by

∗

)(α



),β



)) = g

((F ◦ α)



), (F ◦ β)



))

for all smooth curves α and β in M

with α(t

)=β(t

). Then the condition

that F be a conformal diﬀeomorphism says simply that

∗

=Ω

andinthiscasewewillrefertog

and F

∗

as conformally related metrics

on M

If F happens not to be surjective, but maps only onto some manifold

F (M

) contained in M

,thenF is called a conformal embedding of M

into

and, if 0 < Ω(p) < 1foreachp ∈ M

, is thought of as “squeezing” M

into M

Example 4.5.1 We deﬁne a map F : dS →Eas follows. Let (φ

,φ

,θ,t

)

denote the conformal coordinates on dS (Example 4.3.3)and(

θ, t

)

the coordinates on E deﬁned by (4.5.1). Our map will send the point in

dS with co

dinates (φ

,φ

,θ,t

)tothepointinE with coordinates

(

θ, t

). Somewhat more precisely, we write χ and ¯χ for the co-

ordinate patches on dS and E corresponding to these coordinates and deﬁne

F by

(¯χ

−1

◦ F ◦ χ)(φ

,φ

,θ,t

)=(

θ, t

that is,

= φ

θ = θ (4.5.5)

= t

Since −

, the image of dS in E is the ﬁnite cylinder S



−



Now let α be a smooth curve in dS written as

α(t)=χ(φ

(t),φ

(t),θ(t),t

(t)).

Then



(t)=

dφ

dθ

4.5 Inﬁnity in Minkowski and de Sitter Spacetimes 261

where each χ

is evaluated at α(t). Moreover,

(F ◦ α)(t)=(F ◦ χ)(φ

(t),φ

(t),θ(t),t

(t))

=¯χ



(¯χ

−1

◦ F ◦ χ)(φ

(t),φ

(t),θ(t),t

(t))



=¯χ(

(t),

θ(t),t

(t))

(F ◦ α)



(t)=

¯χ

dφ

¯χ

dφ

¯χ

dθ

¯χ

= F

∗α(t)

(α



(t)),

where each ¯χ

is evaluated at F (α(t)). In particular,

∗p

(χ

(p)) = ¯χ

(F (p)),i=1, 2, 3, 4.

Writing g

for the restriction to S



−



⊆Eof the metric on E given by

(4.5.2) we compute the components of F

∗

in conformal coordinates on dS.

∗

)(χ

(p),χ

(p)) = g



∗p

(χ

(p)),F

∗p

(χ

(p))



= g

(¯χ

(F (p)), ¯χ

(F (p)))

⎧

⎪

⎨

⎪

⎩

0 ,i= j

1 ,i= j =1

sin

(F (p)) ,i= j =2

sin

(F (p)) sin

(F (p)) ,i= j =3

−1 ,i= j =4

⎧

⎪

⎨

⎪

⎩

0 ,i= j

1 ,i= j =1

sin

(p) ,i= j =2

sin

(p)sin

(p) ,i= j =3

−1 ,i= j =4

Consequently, the line element for the metric F

∗

on dS in conformal coor-

dinates (φ

,φ

,θ,t

)is

dφ

+sin



dφ

+sin

dθ



− dt

andthis,accordingtoExercise4.3.18,iscos

times the line element for

the metric g

of dS in conformal coordinates. We conclude therefore that

∗

=Ω

262 4 Prologue and Epilogue: The de Sitter Universe

where Ω(φ

,φ

,θ,t

)=cost

.Thus,F

∗

and g

are conformally related

metrics on dS or, said otherwise, F is a conformal embedding of dS into E.

We will have more to say about this particular example shortly, but ﬁrst

we will need to develop a few general results on conformally related metrics.

First observe that a conformal diﬀeomorphism of one spacetime manifold to

another carries spacelike, timelike and null curves onto curves of the same

type since

((F ◦ α)



(t), (F ◦ α)



(t)) = Ω

(α(t)) g

(α



(t),α



(t))

so the causal character of the tangent vector is preserved at each point. It is

not the case, however, that conformal diﬀeomorphisms always carry geodesics

onto geodesics. However, we will show that a conformal diﬀeomorphism on

a spacetime manifold carries a null geodesic onto a (reparametrization of a)

null geodesic.

We begin by having another look at the geodesic equations

+Γ

=0,r=1,...,n (4.5.6)

in an n-manifold M with metric g. We recall (Lemma 4.3.1) that these

geodesic equations are not independent of parametrization. Indeed, a geodesic

must be parametrized in a very particular way in order for its coordinate

functions to satisfy (4.5.6). These are called aﬃn

par

ametrizations and they

diﬀer from each other by simple linear functions. Of course, any curve can be

reparametrized anyway you like and we would like to see what the geodesic

equations look like in an arbitrary parametrization. Thus, we assume that

(4.5.6) is satisﬁed and introduce a reparametrization t = h(s),

wher

e h is

some

smooth function with h



(s) > 0 for all s.Then





and so

+Γ





+Γ











+Γ



/ds

dt/ds

4.5 Inﬁnity in Minkowski and de Sitter Spacetimes 263

+Γ



t/ds

dt/ds



,r=1,...,n. (4.5.7)

Thus, (4.5.7) are the equations satisﬁed by a geodesic when expressed in

erms

of an arbitrary parameter s. Of course, when s is a linear function of

the aﬃne parameter t, they reduce to (4.5.6).

tice that

if we are given some smooth curve α(s)inM that satisﬁes

+Γ

= f (s)

,r=1,...,n (4.5.8)

for some function f(s), we can introduce a parameter t by setting

t/ds

dt/ds

= f(s)

and solve

− f(s)

to obtain

= e

;

f(ξ)dξ

where a is an arbitrary constant. Reparametrized in terms of t, α(t)satisﬁes

(4.5.6) and is therefore a geodesic of M.

e w

ill write out a speciﬁc example

shortly, but ﬁrst we use this to show that if α(t)isanull geodesic in a

spacetime manifold M (with aﬃne parameter t), then α(t) is also a null

geodesic in any conformally related metric, although t need not be an aﬃne

parameter for it. Thus, conformal diﬀeomorphisms preserve null geodesics, up

to parametrization. For the proof we will ﬁrst need to compute the Christoﬀel

symbols of a conformally related metric.

We let M denote an n-manifold with metric g and suppose ¯g =Ω

g is a

conformally related metric on M. In any coordinate system x

,...,x

the

metric components are g

and ¯g

=Ω

and the entries of the inverse

matrices are related by ¯g

=Ω

−2

. By deﬁnition, the Christoﬀel symbols

for g in these coordinates are



∂g

∂x

∂g

∂x

−

∂g

∂x



, r,i,j =1,...,n