Naber G.L. The Geometry of Minkowski Spacetime. An Introduction to the Mathematics of the Special Theory of Relativity

Подождите немного. Документ загружается.

244 4 Prologue and Epilogue: The de Sitter Universe

which the metric components ˜g

are ˜g

= δ

(so that the line element is

=(d˜x

)

+ ···+(d˜x

)

).AccordingtoExercise4.3.11,

∂˜x

∂x

∂˜x

∂x

˜g

∂˜x

∂x

∂˜x

∂x



a=1

∂˜x

∂x

∂˜x

∂x

,i,j=1,...,n (4.3.29)

on the intersection. Now, (4.3.29) is equivalent to the matrix equation



∂˜x

∂x







∂˜x

∂x



. (4.3.30)

For any invertible matrices A and B,

A = B



B =⇒ A

−1

= B

−1



)

−1

=⇒ BA

−1



=id

so (4.3.30) implies



∂˜x

∂x



)



∂˜x

∂x





=id.

Written out in detail this gives

∂˜x

∂x

∂˜x

∂x

= δ

,a,b=1,...,n. (4.3.31)

Now diﬀerentiate (4.3.29) with respect to x

to obtain

∂g

∂x



a=1



∂˜x

∂x

∂

˜x

∂x

∂˜x

∂x

∂

˜x

∂x



Exercise 4.3.28 Write out similar expressions for

∂g

∂x

and

∂g

∂x

and combine

them to get



∂g

∂x

∂g

∂x

−

∂g

∂x





a=1

∂

˜x

∂x

∂˜x

∂x

. (4.3.32)

Next ﬁx some index b =1,...,n and multiply on both sides of (4.3.32)by

iβ

∂˜x

∂x

(summed over β =1,...,n)

4.3 Mathematical Machinery 245

and then sum over i as required by the summation convention to obtain

βi



∂g

∂x

∂g

∂x

−

∂g

∂x

+

∂˜x

∂x



a=1



∂˜x

∂x

iβ

∂˜x

∂x



∂

˜x

∂x



a=1

∂

˜x

∂x

∂

˜x

∂x

Thus,

∂

˜x

∂x

=Γ

∂˜x

∂x

,b,j,k=1,...,n. (4.3.33)

Now ﬁx an index b =1,...,n and let

=(J

,...,J



∂˜x

∂x

,...,

∂˜x

∂x



be the vector whose components are the entries in the b

row of the Jacobian.

Then (4.3.33) can be written

∂J

∂x

=Γ

bβ

,j,k=1,...,n.

For each j, k, l =1,...,n,wemusthave

∂

∂x

∂

∂x

∂

∂x



bβ



∂

∂x



bβ



∂J

bβ

∂x

∂Γ

∂x

bβ

=Γ

∂J

bβ

∂x

∂Γ

∂x

bβ

βl

bγ

∂Γ

∂x

bγ

=Γ

βk

bγ

∂Γ

∂x

bγ



∂Γ

∂x

+Γ

βk

−

∂Γ

∂x

− Γ

βl



bγ

=0. (4.3.34)

Now for some notation. For each γ, j, k, l =1,...,n,let

jkl

∂Γ

∂x

+Γ

βk

−

∂Γ

∂x

− Γ

βl

. (4.3.35)

246 4 Prologue and Epilogue: The de Sitter Universe

Then we can write (4.3.34)as

jkl

bγ

=0,j,k,l=1,...,n.

We conclude that

jkl

∂˜x

∂x

=0, b,j,k,l=1,...,n. (4.3.36)

Now, for any ﬁxed j, k, l =1,...,n,(4.3.36) can be regarded as a homoge-

neou

s s

ystem of linear equations in

jkl

,...,R

jkl

and, since the Jacobian



∂ ˜x

∂x



is nonsingular, we conclude that

jkl

=0, γ,j,k,l =1,...,n. (4.3.37)

The conclusion of this long and rather annoying calculation is this. If there

exist coordinates ˜x

,...,˜x

on some open set ˜χ(

U)inM relative to which

the metric components are ˜g

= δ

,i,j =1,...,n, then, for any other co-

ordinates x

,...,x

on some open set χ(U)withχ(U) ∩ ˜χ(

U) = ∅,the

functions R

jkl

of x

,...,x

deﬁned by (4.3.35) must vanish identically on

−1

(χ(U) ∩ ˜χ(

U)).

Remarkably enough, the converse is also true, in the following sense.

Rather than supposing the existence of coordinates ˜x

,..., ˜x

with ds

(d˜x

)

+ ···+(d˜x

)

and regarding (4.3.29) as a consequence, let us think of



a=1

∂˜x

∂x

∂˜x

∂x

= g

,i,j=1,...,n. (4.3.38)

as a system of partial diﬀerential equations to be solved for ˜x

,...,˜x

A solution would provide the transformation equations to a new system of

coordinates in which ˜g

= δ

and it can be shown that a solution exists

whenever the “integrability conditions” R

jkl

=0,γ,j,k,l =1,...,n,aresat-

isﬁed (see pages 200–204 of [Sp

], Volume III).

Consequently, the 4

functions R

jkl

deﬁned by (4.3.35) are the replacement

for the Gaussian curvature of a surface in dimensions greater than or equal

to 3. These are called the components (relative to χ)oftheRiemann curvature

tensor R for M .

Remark: We have not deﬁned the unmodiﬁed term “tensor” and will have

no need to do so. However, our experience with 4-tensors in Section 3.1

should leave little room for doubt as to the proper deﬁnition. Recall that

a 4-tensor of contravariant rank 1 and covariant rank 3 can be thought of

as an object described in each admissible frame of reference by 4

= 256

4.3 Mathematical Machinery 247

numbers T

bcd

,a,b,c,d =1, 2, 3, 4, with the property that if two admissible

frames are related by ˆx

=Λ

,a=1, 2, 3, 4, then the numbers that

describe the 4-tensor in the two frames are related by

bcd

=Λ

βγδ

a, b, c, d =1, 2, 3, 4. Noting that Λ

∂ ˆx

∂x

and Λ

∂x

∂ ˆx

, etc., this can be

written

bcd

∂ˆx

∂x

∂ˆx

∂x

∂ˆx

∂x

∂ˆx

βγδ

The transformation law for the metric in Exercise 4.3.11 together with a very

health

y s

upply of persistence gives an entirely analogous transformation law

bcd

∂˜x

∂x

∂˜x

∂x

∂˜x

∂x

∂˜x

βγδ

for the components of R and it is this transformation law that qualiﬁes R as

a“tensor.”

In dimension 4 the Riemann curvature tensor has 4

= 256 components in

every coordinate system, although various symmetries reduce the number of

independent components to 20. Computing even one of these directly from the

deﬁnition (4.3.35) is, needless to say, an arduous task in general. Nevertheless,

ery

one

should do it once in their lives.

Example 4.3.9 We consider the de Sitter spacetime dS in global coordi-

nates x

= φ

= θ and x

= t

. The nonvanishing Christoﬀel

symbols (from Exercise 4.3.22)are

=cosht

sinh t

=cosht

sinh t

sin

=cosht

sinh t

sin

=Γ

sinh t

cosh t

,i=1, 2, 3

= −sin φ

cos φ

= −sin φ

cos φ

sin

= −sin φ

cos φ

=Γ

cos φ

sin φ

=Γ

cos φ

sin φ

We will compute

343

∂Γ

∂x

+Γ

β4

−

∂Γ

∂x

− Γ

β3

248 4 Prologue and Epilogue: The de Sitter Universe

First note that

∂Γ

∂x

∂

∂t

(cosh t

sinh t

sin

)

=(cosh

+sinh

)sin

sin

and

∂Γ

∂x

∂

∂θ

(0) = 0.

Next we have

β4

=Γ

+Γ

since each Γ

β4

= 0. Finally,

β3

=Γ

+Γ

=0+0+Γ



sinh t

cosh t



(cosh t

sinh t

sin

)

=sinh

sin

Thus,

343

=cosh

sin

Exercise 4.3.29 Show that, for the de Sitter spacetime in global coordi-

nates,

4i4

= −1

for i =1, 2, 3.

Remark: Observe that, in dS,

− δ

= g

=cosh

sin

= R

343

(δ

=1ifa = b and 0 if a = b is just the Kronecker delta). Also,

− δ

= g

= −1=R

4i4

for i =1, 2, 3. As it happens, one can show that

jkl

= δ

− δ

(4.3.39)

for all γ,i, j,k =1, 2, 3, 4. Thus, for example, setting k = γ and summing

over γ gives

jγl

= δ

− δ

jγ

=4g

− g

=3g

Remark: A manifold M with metric g is said to have constant (sectional)

curvature if there is a constant K such that

jkl

= K (δ

− δ

)

4.4 The de Sitter Universe dS 249

in any local coordinate system. de Sitter spacetime dS therefore has constant

curvature K = 1. We will encounter this notion again in the next section.

The Riemann curvature tensor contains all of the information about a

manifold’s local deviations from “ﬂatness” and, in the case of a spacetime,

this is precisely what we mean by a gravitational ﬁeld (see Section 4.1). It is,

however, a rather cumbersome creature and one can often make due (both

mathematically and physically) with somewhat simpler objects that we now

introduce. For any n-manifold M with (Riemannian or Lorentzian) metric g

we deﬁne, in any local coordinate system on M,thecomponents of the Ricci

tensor R

= R

iγj

(sum over γ =1,...,n)

for i, j =1,...,n.Thescalar curvature R of M is then deﬁned by

R = g

(sum over i, j =1,...,n).

According to the previous Remark, the Ricci tensor of de Sitter spacetime

dS is

=3g

and so

R = g

= g

(3g

)=3g

=3δ

=3(4)=12.

Remark: The scalar curvature is generally a real-valued function on M,

but in the case of dS happens to be a constant function.

Finally, we deﬁne, in any local coordinate system for M,thecomponents of

the Einstein tensor G

= R

−

for i, j =1,...,n.Thus,fordS,

=3g

−

(12) g

= −3g

Exercise 4.3.30 Show that G

=0foralli, j =1,...,n if and only if

=0foralli, j =1,...,n. Hint: Assuming G

=0,considerg

4.4 The de Sitter Universe dS

A spacetime, as we have deﬁned it, is a 4-dimensional manifold with a Lorentz

metric. The motivation behind the deﬁnition was an attempt to model the

event world when gravitational eﬀects cannot be regarded as negligible. It

is certainly not the case, however, that every spacetime represents some

250 4 Prologue and Epilogue: The de Sitter Universe

physically realistic gravitational ﬁeld. Einstein’s idea was that the space-

time should be “determined” by the mass-energy distribution giving rise to

the gravitational ﬁeld and he struggled for many years to arrive at equations

that speciﬁed just how the latter determined the former. The end result of

the struggle was a set of ten coupled nonlinear partial diﬀerential equations

for the metric components g

called the Einstein ﬁeld equations. It is with

these that the general theory of relativity begins and we will not be so bold

as to oﬀer a precis of their derivation. We simply record the equations, make

a few unremarkable observations and then move on to their relevance to our

story. A spacetime M with Lorentz metric g is said to satisfy the Einstein

ﬁeld equations if, in any local coordinate system,

−

+Λg

=8πT

,i,j=1, 2, 3, 4, (4.4.1)

where R

−

= G

is the Einstein tensor, Λ is a constant, called the

cosmological constant,andT

is called the energy-momentum tensor and is

a direct analogue of the energy-momentum transformation for the electro-

magnetic ﬁeld on Minkowski spacetime that we introduced in Section 2.5.

The role of T

is to describe the mass-energy distribution giving rise to the

gravitational ﬁeld being modeled by g

. The equations relate the geometry

of the spacetime, described by the left-hand side, to the mass-energy distri-

bution, described by the right-hand side. Together with the so-called geodesic

hypothesis that free particles have worldlines in M that are timelike or null

geodesics, (4.4.1) contains essentially the entire content of general relativity.

The left-and right-hand sides of (4.4.1) have the same transformation law

to a new system of local coordinates



∂x

∂˜x

∂x

∂˜x



so, if they are

satisﬁed for one set of charts covering M , they are satisﬁed in any coordinate

system (they are “tensor equations”). In particular, it makes sense to deﬁne

an empty space solution to Einstein’s equations to be a spacetime satisfying

(4.4.1) with T

=0,i,j=1, 2, 3, 4.

Exercise 4.4.1 Show that the de Sitter spacetime dS is an empty space

solution to the Einstein equations with Λ = 3.

Remark: It may strike the reader as peculiar that we introduce “empty

space solutions” since our motivation has been to model nontrivial gravita-

tional ﬁelds. Let us explain. When Λ = 0 the empty space equations are

= 0 which, by Exercise 4.3.30,arethesameas

=0. (4.4.2)

Manifolds satisfying (4.4.2)aresaidtobeRic

ﬂat and, in general relativ-

ity, they are regarded as an analogue of the source free Maxwell equations

introduced in Section 2.7. Solutions describe gravitational ﬁelds in regions of

spacetime in which the mass-energy giving rise to the ﬁeld is “elsewhere.”

4.4 The de Sitter Universe dS 251

The best known example is the Schwarzschild solution describing the ﬁeld

exterior to a spherically symmetric mass/star (see Chapter Six of [Wald]).

the o

ther hand, when Λ = 0, the empty space equations are

+Λg

= 0 (4.4.3)

and here the interpretation is more subtle. One might, for example, rewrite

(4.4.3)as

=8π



−

8π



(4.4.4)

and regard

vac

= −

8π

(4.4.5)

as an energy-momentum tensor for some unspeciﬁed mass-energy distribution

and (4.4.4) as the Einstein equations with cosmological constant zero. In this

inter

etation, (4.4.5) is often thought of as the energy-momentum of the vac-

uum, due

rhaps to quantum ﬂuctuations of the vacuum state required by

quantum ﬁeld theory. In this guise, T

vac

is often attributed to what has come

to be called “dark energy.” Alternatively, one could simply regard the cosmo-

logical term Λg

in Einstein’s equations (4.4.1) as a necessary ingredient in

the basic laws of physics, independent of any mass-energy interpretation. In

this case one has solutions like dS representing a genuinely “empty” universe,

but which are, nevertheless, not ﬂat (dS has nonzero curvature tensor). Such

solutions therefore represent alternatives to Minkowski spacetime with very

diﬀerent mathematical and, as we shall see, physical properties.

It is not the usual state of aﬀairs, of course, to be given a spacetime and an

energy-momentum tensor and be asked to check (as in Exercise 4.4.1) that

together they give a solution to the Einstein equations. Rather, one would

begin with some physical distribution of matter and energy (an electromag-

netic ﬁeld, a single massive object such as a star, or an entire universe full

of galaxies) and one would attempt to solve the equations (4.4.1) for the

metric. Aside from the enormous complexity of the equations (express R

and R directly in terms of g

and substitute into (4.4.1)) there are subtleties

in this that may not be apparent at ﬁrst glance. The Einstein equations are

written in coordinates, but coordinates on what? The objective is to con-

struct the manifold and its metric so neither can be regarded as given to

us. To solve (4.4.1) one must begin with a guess (physicists prefer the term

“ansatz”) based on one’s physical intuition concerning the ﬁeld being mod-

eled as to what at least one coordinate patch on the sought after manifold

might look like. Even if one should succeed in this, the end result will be no

more than a local expression for the metric in one coordinate system; the

rest of the manifold is still hidden from view. Moreover, it is the metric it-

self that determines the spacetime measurements in the manifold. Since one

cannot describe energy and momentum without reference to space and time

measurements, even T

cannot be regarded as given, but depends on the un-

known metric components g

. Even the true physical meaning of the ansatz

coordinates cannot be known until after the equations are solved.

252 4 Prologue and Epilogue: The de Sitter Universe

All of these subtleties add spice to the problem of solving the Einstein

equations, but this is not really our concern here. We would, however, like to

say a few words about the ansatz appropriate to what are called cosmological

models (spacetimes intended to model the global structure of the universe as

awhole).Forthisweneedjustonemoremathematicaltool.

Let M

and M

be two smooth manifolds and F : M

→ M

asmooth

map. At each point p ∈ M, we deﬁne the derivative F

∗p

of F at p to be

the map

∗p

: T

) → T

F (p)

)

that carries the velocity vector of a smooth curve α in M

through p to the

velocity vector of its image F ◦ α under F , i.e.,

∗p

(α



)) = (F ◦ α)



In this way smooth maps carry tangent vectors in the domain to tangent

vectors in the range. Now suppose M

and M

have metrics g

and g

,re-

spectively (both Riemannian or both Lorentzian) and that F : M

→ M

a diﬀeomorphism. Then F is called an isometry if it preserves inner products

at each point, i.e., if

(α



),β



)) = g

((F ◦ α)



), (F ◦ β)



))

for all smooth curves α and β in M

with α(t

)=β(t

). In particular,

an isometry of a manifold M with metric onto itself is the analogue of an

orthogonal transformation of a vector space with inner product onto itself. In

particular, the collection of all such form a group, called the isometry group

of M .FordS this group is precisely the set of restrictions to dS of orthogonal

transformations of M

and is called the de Sitter group (this result is not

obvious, but we do not need it and so will not prove it). For spacetimes,

isometries are our new Lorentz transformations.

The two most basic physical assumptions that go into the construction of a

cosmological model in general relativity are called “spatial homogeneity” and

“spatial isotropy.” Intuitively, these assert that, at any “instant”, all points

and all directions in “space” should “look the same.” Since “instant” and

“space” are the very things that relativity forbids us ascribing a meaning to

independent of some observer, it is not so clear what this is supposed to mean.

We will attempt a somewhat more precise statement of what is intended. A

spacetime M is said to be spatially homogeneous and isotropic if the following

conditions are satisﬁed (see Figure 4.4.1).

(A)

There exists

a f

amily of free observers (future-directed, timelike

geodesics) with worldlines ﬁlling all of M (for each p ∈ M there exists

one and only one of these geodesics α

with α

)=p for some value

of proper time on α

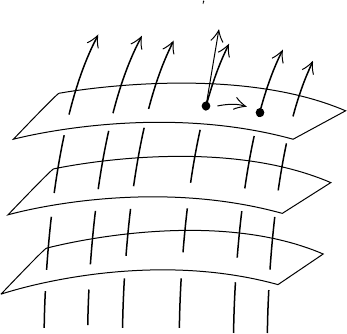
4.4 The de Sitter Universe dS 253

(B) There exists a 1-parameter family of spacelike hypersurfaces Σ

(3-

dimensional manifolds in M on which the restriction of the spacetime

metric g is positive deﬁnite) that are pairwise disjoint and ﬁll all of M.

,thenα



) is orthogonal to T

(Σ

) (so that the

hypersurfaces can be regarded as common “instantaneous 3-spaces” for

the observers).

(D) If p, q ∈ Σ

, then there is an isometry of M onto itself that carries p to

q (“at each instant all points of space look the same”).

(E) If p = α

)isinΣ

and u

are two directions (unit vectors)

in T

(Σ

), then there is an isometry of M onto itself that leaves p and



) ﬁxed, but “rotates” u

onto u

(“at each instant all directions

at any point in space look the same to the observer experiencing that

event”).

)

Fig. 4.4.1

As it happens, these conditions are quite restrictive. Based on them one

can show (see Section 5.1 of [Wald]) that each of the spacelike hypersurfaces

n (

B), with the metric obtained by restricting g to Σ, is a manifold of

constant curvature (see the Remark following (4.3.39)). Now, up to certain

“top

ologi

cal” variations that are not relevant to our purpose here, one can

enumerate all of the 3-dimensional Riemannian manifolds of constant curva-

ture. They are 3-spheres (K>0), 3-dimensional Euclidean spaces (K =0)

and hyperbolic 3-spaces (K<0), all of which we have seen before.

The idea behind the “cosmological ansatz” can then be described as fol-

lows. Select one of the spacelike hypersurfaces Σ and choose coordinates on it

so that its line element is of one of the following forms (we will use the same

names for the coordinates in all cases in order to exhibit the similarities).