Naber G.L. The Geometry of Minkowski Spacetime. An Introduction to the Mathematics of the Special Theory of Relativity

Подождите немного. Документ загружается.

264 4 Prologue and Epilogue: The de Sitter Universe

and those for ¯g are

¯g



∂¯g

∂x

∂¯g

∂x

−

∂¯g

∂x



−2



∂

∂x





∂

∂x





−

∂

∂x







−2



∂g

∂x

+2Ω

∂Ω

∂x

∂g

∂x

+2Ω

∂Ω

∂x

−

∂g

∂x

− 2Ω

∂Ω

∂x



=Γ

+Ω

−1



∂Ω

∂x

∂Ω

∂x

−

∂Ω

∂x



=Γ

+Ω

−1



∂Ω

∂x

+ δ

∂Ω

∂x

− g

∂Ω

∂x



Thus,

=Γ

+ δ

∂

∂x

(ln Ω) + δ

∂

∂x

(ln Ω) − g

∂

∂x

(ln Ω). (4.5.9)

Next we consider a curve α(t) in a spacetime M that is null relative to g,

and therefore also relative to ¯g.Thus,

= 0 (4.5.10)

for all t. We claim that (4.5.10) implies

+Γ

(2 ln Ω)

(4.5.11)

for r =1, 2, 3, 4. Indeed, multiplying (4.5.9)by

and summing as indi-

cated gives

− Γ

= δ

∂

∂x

(ln Ω)

+ δ

∂

∂x

(ln Ω)

− g

∂

∂x

(ln Ω) g



∂

∂x

(ln Ω)

∂

∂x

(ln Ω)



− 0

4.5 Inﬁnity in Minkowski and de Sitter Spacetimes 265



∂

∂x

(ln Ω)





(ln Ω)



from which (4.5.11) is immediate.

Now we

can fulﬁll our promise about null geodesics. Suppose that α(t)is

a null geodesic of g with aﬃne parameter t.Then(4.5.10) is satisﬁed and,

reo

ver,

+Γ

=0,r=1, 2, 3, 4.

Thus, (4.5.11)gives

(2 ln Ω)

, (4.5.12)

for r =1, 2, 3, 4. It follows from (4.5.8)thatα(t) is also a (null) geodesic of ¯g,

but

that t is

not an aﬃne parameter for it. From the discussion immediately

following (4.5.8) we can introduce an aﬃne parameter μ fo

r this

null geodesic

of ¯g by

dμ

=exp





dξ

(2 ln Ω)dξ



Taking the multiplicative constant to be one,

dμ

=Ω



(t),...,x

(t)



(4.5.13)

so μ(t) can be found by integration.

Example 4.5.2 We return to the conformally related metrics g

and

∗

on dS discussed in Example 4.5.1.HereF

∗

=Ω

,where

Ω(φ

,φ

,θ,t

)=cost

. Every null geodesic in dS (relative to g

)can

be described as follows.

Fix a point p ∈ dS and a null vector v in M

orthogonal to p in M

((v, v)=0

and (p, v) = 0). Then any linear parametrization α(t)=p + tv, −∞ <t<

∞, of the straight line through p in the direction v is a null geodesic of

dS.Anysucht is an aﬃne parameter for the geodesic since the acceleration

is zero which is certainly M

-orthogonal to T

α(t)

(dS )foreacht and this,

as we have seen, implies that the geodesic equations (4.3.27)aresatisﬁed

in a

coordinate system. Since a null straight line in M

can be linearly

parametrized by u

we can assume that p is in the “bottleneck” u

=0indS

and simply take t to be u

Exercise 4.5.5 Show that u

=tan(t

)for−

Now, we have seen that α is also a reparametrization of a null geodesic of

∗

and that an aﬃne parameter μ for this F

∗

-geodesic is determined by

(4.5.13) which, in this case, is

266 4 Prologue and Epilogue: The de Sitter Universe

dμ

=cos

(t))

=cos

(arctan t)byExercise4.5.5

1+t

μ = μ(t) = arctan t + k = t

+ k

for some constant k.Takingk =0sothat

μ =0 ⇐⇒ t =0 ⇐⇒ t

we ﬁnd that

μ = t

is an aﬃne parameter for α(t) with respect to F

∗

Rephrasing all of this we conclude that the image in E of the null geodesic

α(t)indS under the conformal diﬀeomorphism F is that portion of a null

geodesic (“helix”) in E aﬃnely parametrized by t

= t

for −

(see Figure 4.5.3). The most important conclusion we wish to draw from this

is that, on null geodesics,

t −→ ∞ ⇐⇒ t

−→

and

t −→ −∞ ⇐⇒ t

−→ −

Thus, the entire history of a null geodesic in dS is “squeezed” into the ﬁnite

region −

of E and the slices t

= −

and t

accurately

represent “inﬁnity” for null geodesics in dS. The 3-sphere t

= −

in E is

denoted I

−

and called the past null inﬁnity of dS ; t

, denoted I

,is

the future null inﬁnity of dS.IfweidentifydS with its “squeezed” version

in E, one can think of null geodesics as being born on I

−

in the inﬁnite past

(t = −∞) and dying on I

in the inﬁnite future (t = ∞).

There is a great deal of information in this conformal picture about the

causal structure of dS, much of which contrasts rather sharply with what

we know about Minkowski spacetime. It is all much more easily visualized,

however, if we construct something analogous to the 2-dimensional Minkowski

diagrams employed in Chapter 1. These are called Penrose diagrams and are

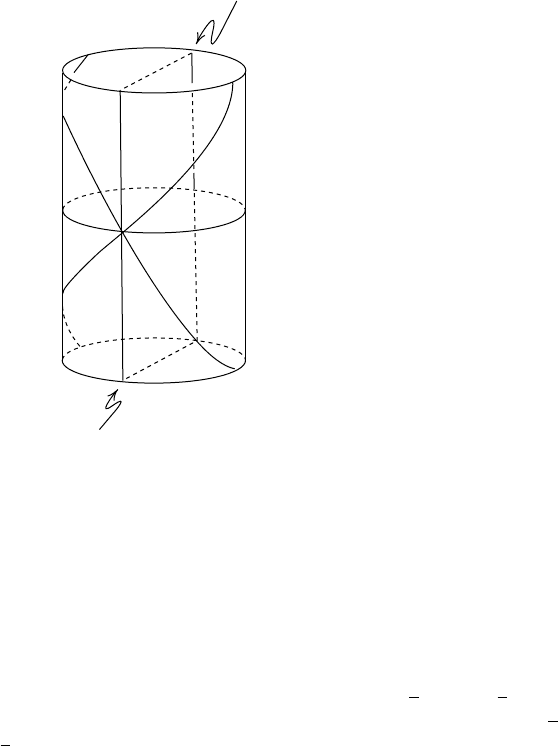
based on the simple fact that the helices representing null geodesics of E in

Figures 4.5.2 and 4.5.3 are precisely the curves on the cylinder that one gets

agon

strai

ght lines in the plane by wrapping the plane around itself

to build the cylinder. We reverse this procedure by cutting the cylinder in

Figure 4.5.3 along the vertical line at φ

= π and ﬂattening it onto the plane.

The result is Figure 4.5.5 which also has labeled a number of additional items

tha

will

w endea

vor to explain.

4.5 Inﬁnity in Minkowski and de Sitter Spacetimes 267

= π

= 0

= −

(t → - ∞ )

−

(t → ∞)

−

Fig. 4.5.3

We will identify the timelike hyperbolas in Figure 4.5.4 with the worldlines

of a family of cosmic observers in dS for which φ

(as well as φ

and θ)are

held ﬁxed and will (arbitrarily) decree that the observer with φ

=0resides

at the north pole of S

Then φ

= π corresponds to an observer at the south

pole. These worldlines map to vertical straight lines in the conformal image of

dS in E and we will now identify these, parametrized by −

,with

our cosmic observers. The points on these vertical straight lines with t

and t

= −

do not arise from points on the hyperbolas in dS.Rather,they

are to be regarded as the asymptotic limits of these worldlines as t →∞and

t →−∞, respectively.

We begin by focusing attention on some point p on the worldline of the

observer O residing at the north pole. The null geodesics through p (or any

other point) appear as straight lines inclined 45

◦

to the horizontal. We will,

somewhat inaccurately, refer to this pair of lines as the “null cone” at p

(technically, the null cone lives in the tangent space at p). The events on the

lower (past) null cone at p are those visible to O at p. Notice that some of

our cosmic observers have worldlines that intersect this past null cone at p

(e.g., O



at p



), but others. do not (e.g., O



) and the latter are not visible to

O at p. By contrast, in Minkowski spacetime, the past null cone at any event

on any timelike straight line intersects every other timelike straight line. The

268 4 Prologue and Epilogue: The de Sitter Universe

= p (south pole)

= 0 (north pole)

Fig. 4.5.4

past null cone at p is called the particle horizon of O at p since it is the

boundary between the particles that are visible to O at or before p and those

that are not; such things do not exist in M.TheobserverO



does eventually

become visible to O since the point p



on its worldline is also on the past null

cone at p

. The same cannot be said of an observer stationed at the south

pole, however, since no past null cone to any point on O’s worldline intersects

the vertical line at φ

= π.

The past null cone at the point in E with φ

=0andt

does not

correspond to any point on the worldline of O, but is rather to be regarded

as a limiting position for O’s past null cones as t →∞. This is called the

past event horizon of the worldline and is the boundary between the events

that will eventually be visible to O and those that will not. Notice that the

worldlines of O



and O



both intersect this past event horizon (at p



and



). These are perfectly ordinary points on the worldlines of O



and O



, but

O never sees them because an inﬁnite proper time elapses on O’s worldline

before they occur. O sees a ﬁnite part of the history of both O



and O



in an

inﬁnite amount of his proper time. Physicists would express this by saying

that signals received by O from either O



or O



are redshifted by an amount

that becomes inﬁnite as the points p



and p



are approached.

Analogously, the future null cone at p encloses all of the events that O

can inﬂuence at or after p. The corresponding future null cone at the point

of E with φ

=0andt

= −

encloses all of the events that O could

ever inﬂuence and is called the future event horizon of O’s worldline. The

shaded region in Figure 4.5.5 between the past and future event horizons of

O therefore

consists of ev

ents that are completely inaccessible to O,whocan

neither inﬂuence nor be inﬂuenced by them.

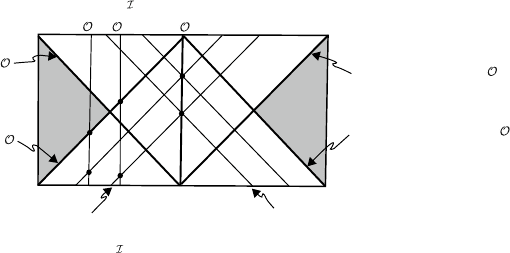
4.5 Inﬁnity in Minkowski and de Sitter Spacetimes 269

= π

Particle Horizon at p Particle Horizon at p

Past Event Horizon of

Future Event Horizon of

Past Event Horizon of

Future Event Horizon of

= π

; t → ∞ )

−

= −

; t → − ∞ )

−

Fig. 4.5.5

All of the behavior we have just described is, of course, completely unheard

of in M. The structure of “inﬁnity” in Minkowski spacetime is clearly diﬀer-

ent than that of de Sitter spacetime. To understand more precisely just what

these diﬀerences are we would like to conclude by guiding the reader through

a sequence of exercises that construct an analogous conformal embedding of

M into E and the resulting Penrose diagram for Minkowski spacetime. The

ﬁrst objective is an analogue of conformal coordinates for M.

It will be convenient to construct these conformal coordinates for M in

stages. We will denote by u

,andu

the standard coordinates on

M(R

) relative to which the Minkowski line element is

=(du

)

+(du

)

+(du

)

− (du

)

Identifying R

with R

×R, introducing spherical coordinates ρ, φ, θ on R

and denoting by t the coordinate on R we have

= ρ sin φ cos θ

= ρ sin φ sin θ

= ρ cos φ

= t

and

= dρ

+ ρ

(dφ

+sin

φdθ

) − dt

We remind the reader of all the usual caveats concerning spherical coordi-

nates. All of M is parametrized by ρ, φ, θ, t with ρ ≥ 0, 0 ≤ φ ≤ π,

0 ≤ θ ≤ 2π,and−∞ <t<∞, but to obtain charts one restricts

these to either ρ>0, 0 <φ<π,0 <θ<2π, −∞ <t<∞,or

ρ>0, 0 <φ<π, −π<θ<π, −∞ <t<∞. These two charts cover

all of M except the u

-axis for each u

(= t). One can cover these points,

270 4 Prologue and Epilogue: The de Sitter Universe

except for ρ = 0, with analogous spherical coordinates with, say, φ measured

from the u

-axis and θ in the u

-plane. Finally, to cover the points with

ρ =0, −∞ <t<∞, i.e., the t-axis, one selects some other point as the

“origin” for an entirely analogous spherical coordinate chart. As is custom-

ary, we sweep all of these variants under the rug and use ρ, φ, θ, t for the

coordinates in any one of these charts.

Next we introduce what are called advanced and retarded null coordinates

v and w by letting v = t + ρ and w = t −ρ. In somewhat more detail, we let

ρ =

(v − w)

φ = φ

θ = θ (4.5.14)

t =

(v + w)

Exercise 4.5.6

(a) Show that v, w, φ, θ parametrize all of M for −∞ <w≤ v<∞, 0 ≤

φ ≤ π and 0 ≤ θ ≤ 2π and that each point of M iscontainedinanopen

set on which v, w, φ, θ are the coordinates of a chart for M.

(b) Show that, if a and b are constants, then the set of points in M with v = a

is the lower half of the null cone at (u

)=(0, 0, 0,a)and

w = b is the upper half of the null cone at (u

)=(0, 0, 0,b).

(v − w)

(dφ

+sin

φdθ

) − dv dw.

Exercise 4.5.6 (b) provides a nice geometrical and physical interpretation of

the new

coordinates v an

d w. One ﬁnds v and w geometrically at a point x

in M by locating points on the u

-axis at which the lower and upper null

cones intersect at x. Physically, one can express this in the following way.

For v(x) one ﬁnds a spherical electromagnetic wave that is “incoming” to

the origin and experiences x, while for w(x) one ﬁnds such a wave that is

“outgoing” from the origin. Then v(x)isthetimet at which the incoming

wave reaches the origin and w(x)isthetimet at which the outgoing wave

left the origin. Succinctly, one connects x to the origin with light rays and

uses the departure and arrival times as coordinates. Thus, v(x) (respectively,

w(x)) is an advanced (respectively, retarded) null coordinate. Suppressing φ

and θ we can picture this in the ρt-plane as in Figure 4.5.6.

ext

once again use the arctangent function to “make inﬁnity ﬁnite”,

as Penrose and Rindler [PR

] put it. Speciﬁcally, we replace v and w by two

new coordinates p and q deﬁned by p =arctanv and q =arctanw.Inmore

detail, we deﬁne

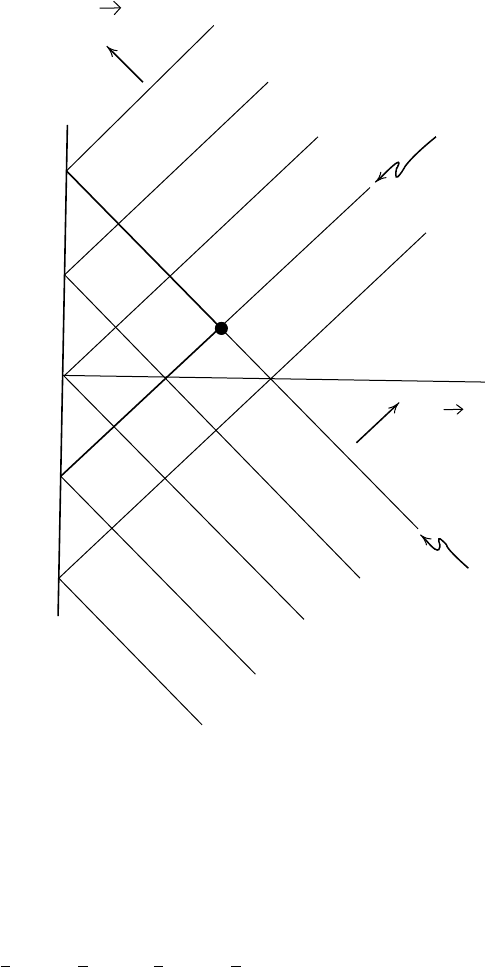
4.5 Inﬁnity in Minkowski and de Sitter Spacetimes 271

∞

= b

= a

Fig. 4.5.6

v =tanp

φ = φ

θ = θ (4.5.15)

w =tanq

for −

<p<

and −

<q<

.Noticethat

w ≤ v =⇒ q ≤ p.

272 4 Prologue and Epilogue: The de Sitter Universe

Exercise 4.5.7

(a) Show that p, q, φ, θ parametrize all of M for −

<q≤ p<

, 0 ≤ φ ≤ π

and 0 ≤ θ ≤ 2π and that each point of M iscontainedinanopenseton

which p, q, φ, θ are the coordinates of a chart for M.

(b) Show that the line element for M in these coordinates is

sec

p sec



−4dp dq +sin

(p − q)



dφ

+sin

φdθ



Now, one ﬁnal maneuver to bring this last line element into a more familiar

form. Speciﬁcally, we introduce two new coordinates t



and ρ



by t



= p + q

and ρ



= p − q, i.e.,

p =



+ ρ



)

φ = φ

θ = θ (4.5.16)

q =



− ρ



)

for −π<t



<πand 0 ≤ ρ



<π.

Exercise 4.5.8

(a) Show that ρ



,φ, θ, t



parametrize all of M for 0 ≤ ρ



<π, 0 ≤ φ ≤

π, 0 ≤ θ ≤ 2π, −π<t



<π,andthateachpointofM is contained in

an open set on which ρ



,φ,θ,t



are the coordinates of a chart for M.

(b) Show that

2t =tan





+ ρ



)



+tan





− ρ



)



2ρ =tan





+ ρ



)



− tan





− ρ



)



sec





+ ρ



)



sec





− ρ



)





dρ

2

sin



(dφ

+sin

φdθ

) − dt

2



. (4.5.17)

Now we ﬁnd ourselves in a familiar position. Except for the names of the

variables, dρ

2

+sin



(dφ

+sin

φdθ

) − dt

2

has precisely the same form

as the line element (4.5.2) of the Einstein static universe in its standard

rdina

tes and the line element for M relative to (ρ



,φ,θ,t



)isjust

a positive multiple of this. We now ask the reader to argue as we did in

Example 4.5.1 and draw the same conclusion.

4.5 Inﬁnity in Minkowski and de Sitter Spacetimes 273

Exercise 4.5.9 Deﬁne a mapping F of M into E by

= ρ



= φ

θ = θ

= t



for 0 ≤ ρ



<π, 0 ≤ φ ≤ π, 0 ≤ θ ≤ 2π and −π<t



<π. Show that F is a

conformal embedding of M into the region S

× (−π, π)inE with

∗

=Ω

where g

is the Lorentz metric on M and

Ω(ρ



)=2cos





+ ρ



)



cos





− ρ



)



. (4.5.18)

The image of the conformal embedding of dS into E was all of



−



, but it is not the case that the map F in Exercise 4.5.9 maps

ont

o S

× (−π, π). To ﬁnd the image we ﬁrst ﬁnd its boundary (which will

eventually play the role of “inﬁnity” in M)). As before we will construct our

picture on the 2-dimensional cylinder by holding φ and θ ﬁxed.

The “ﬁnite part” of M corresponds to −

<q≤ p<

so −π<t



+ ρ



π, −π<t



− ρ



<π,and0≤ ρ



≤ π.Since

= ρ



and t

= t



,these

translate to −π<t

<π, −π<t

−

<π,and0≤

<π.Thus,

the boundary of the image of M in E is determined by t

= ±π and

−

= ±π, subject to 0 ≤

≤ π and −π ≤ t

≤ π. Observe ﬁrst that

= −π, t

≥−π, and

≥ 0=⇒ (t

)=(−π, 0)

and

−

= π, t

≤ π, and

≥ 0=⇒ (t

)=(π, 0)

These two points in our picture we will denote

−

: t

= −π



p = −

,q= −



and

: t

−

= π



p =

,q=



and, for reasons to be explained shortly, call them, respectively, past and

future timelike inﬁnity of M, while those satisfying

−

= −π