Naber G.L. The Geometry of Minkowski Spacetime. An Introduction to the Mathematics of the Special Theory of Relativity

Подождите немного. Документ загружается.

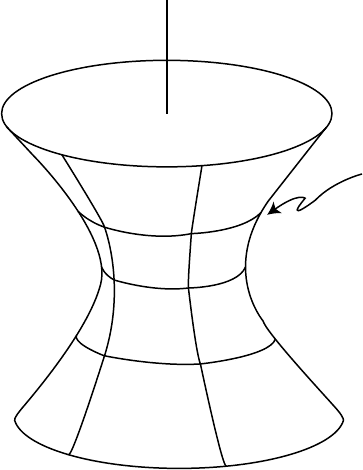
214 4 Prologue and Epilogue: The de Sitter Universe

Fig. 4.3.4

for 0 ≤ φ

≤ π, 0 ≤ φ

≤ π, 0 ≤ θ ≤ 2π,and−∞ <t

< ∞.Then

)

+(u

)

+(u

)

+(u

)

− (u

)

= 1 and the image of the map is all

of D. For any ﬁxed t

, the slice at u

=sinht

is the spherical coordinate

parametrization of the 3-sphere of radius cosh t

Exercise 4.3.5 WriteouttheJacobianofthemap(4.3.11)andshowthat

rank 4 on

0 <φ

<π, 0 <φ

<π, 0 <θ<2π, −∞ <t

< ∞

and

0 <φ

<π, 0 <φ

<π, −π<θ<π, −∞ <t

< ∞

and so provides a chart at the image of each such point. Note that charts

at points with φ

=0,πand φ

=0,π can be obtained by interchanging

standard coordinates on R

We conclude that each point of D iscontainedinanopensetonwhich

(φ

,φ

,θ,t

) are local coordinates and for this reason they are often called

global coordinates for D, although the charts themselves are not globally

deﬁned on D. The motivation behind the remaining parametrizations of D

that we intend to introduce now may appear rather obscure, but will become

clear after we have introduced some geometry into our picture.

4.3 Mathematical Machinery 215

Example 4.3.3 The parametrization of D we introduce here diﬀers from

the global coordinates (φ

,φ

,θ,t

) only in that we will replace t

by a

new fourth coordinate t

that we would like to be related to t

=cosht

=0⇐⇒ t

(the reason we would like this will emerge shortly). Separating variables,

integrating the equation and using the initial condition gives

= 2 arctan(e

) −

(4.3.12)

so that

−

Exercise 4.3.6 Show that

cosh t

cos t

for −

It follows that the mapping (φ

,φ

,θ,t

) → (φ

,φ

,θ,t

)issmoothwith

nonsingular Jacobian for −

and is therefore a local diﬀeomor-

phism. Composing this with the global coordinate parametrization of D we

ﬁnd that each point of D iscontainedinanopensetonwhich(φ

,φ

,θ,t

)

are coordinates. For reasons that we will describe in Section 4.5 these are

called conformal coordinates.

Example 4.3.4 Next we introduce what are called planar coordinates.

These are denoted (t

) and cover only half of D.Theyarise

from the mapping

χ : R

−→ R

deﬁned by

= x

(4.3.13)

=cosht

−

















=sinht

















It is easy to check that (u

)

+(u

)

+(u

)

+(u

)

−(u

)

= 1, but in this

case

+ u

= e

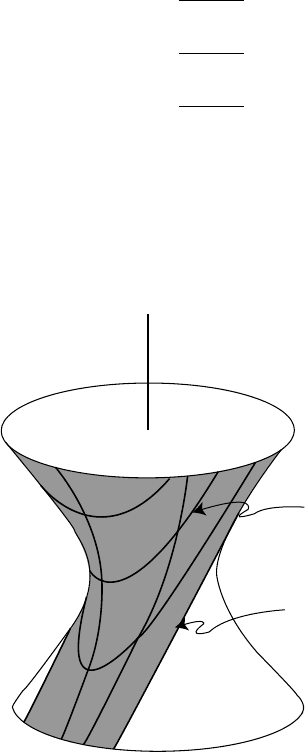
216 4 Prologue and Epilogue: The de Sitter Universe

so only the portion u

+ u

> 0ofD is covered by the image. For these,

=ln(u

+ u

)andso

+ u

(4.3.14)

+ u

=ln(u

+ u

We will denote by D

this portion of D .Thet

= t

slices of D

are the

intersections with D

of the hyperplanes u

+ u

= e

(see Figure 4.3.5).

= 0

Fig. 4.3.5

Exercise 4.3.7 Compute the Jacobian of (4.3.13) and show that it has rank

4 at each point of R

Thus, each point of D

iscontainedinanopensubsetofD

on which

) are coordinates.

4.3 Mathematical Machinery 217

Example 4.3.5 Our ﬁnal parametrization of D provides it with what are

called hyperbolic coordinates (φ, θ, ψ, t

). We will leave the details to the

reader.

Exercise 4.3.8 Deﬁne a smooth map of R

into R

=cosφ sinh t

sinh ψ

=sinφ cos θ sinh t

sinh ψ

=sinφ sin θ sinh t

sinh ψ (4.3.15)

=cosht

=sinht

cosh ψ

(a) Verify that (u

)

+(u

)

+(u

)

+(u

)

− (u

)

=1.

(b) Let t

be a constant and consider the t

= t

slice of D. Show that if

= 0 this slice is a point and if t

= 0 the points on the slice have

=cosht

and

)

+(u

)

+(u

)

− (u

)

= −sinh

and ψ

be two nonzero constants and consider the set of points in

D with t

= t

and ψ = ψ

. Show that u

and u

are constant and φ

and θ parametrize a 2-sphere in (u

)-space.

(d) Compute the Jacobian of (4.3.15) and show that it is nonsingular for

0 <φ

<π

, 0 <θ<

2π, ψ =0,andt

=0.

With these examples in hand we now return to the general development.

Each point on a smooth surface in R

has associated with it a 2-dimensional

“tangent plane” consisting of all the velocity vectors to all smooth curves

in the surface through that point. The analogous construction on a smooth

n-manifold M in R

proceeds as follows. We will write u

,...,u

for the

standard coordinates in R

and use x

,...,x

for standard coordinates in

.IfI ⊆ R is a (nondegenerate) interval, then a continuous map

α : I −→ M

α(t)=(u

(t),...,u

(t))

is called a curve in M. α is said to be smooth if each u

(t),i=1,...,m,is

∞

and if α’s velocity vector (or tangent vector)



(t)=



,...,



is nonzero for each t in I. Useful examples of smooth curves can be con-

structed from a coordinate patch

χ : U −→ M ⊆ R

χ(x

,...,x

)=(u

,...,x

),...,u

,...,x

)).

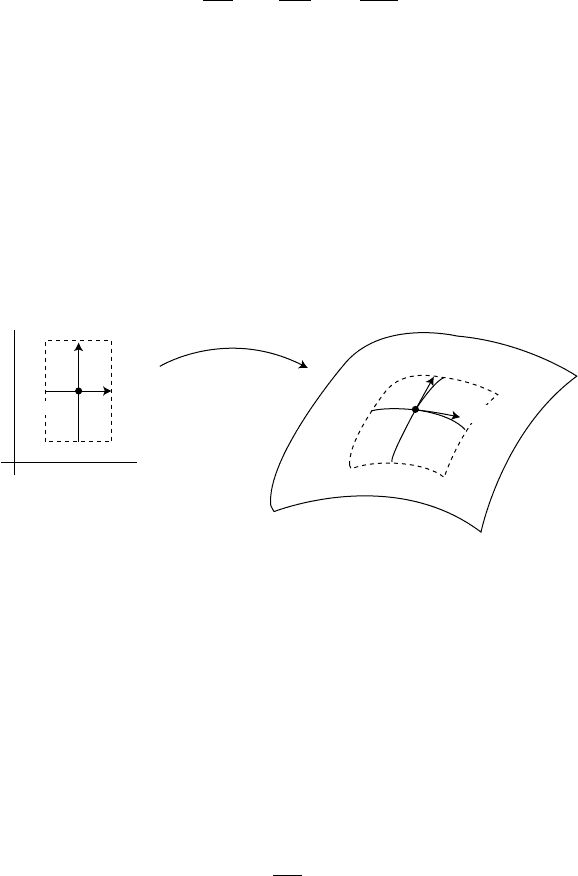
218 4 Prologue and Epilogue: The de Sitter Universe

For each i =1,..., n,thei

coordinate curve of χ is obtained by holding

all x

,j= i,ﬁxed(sot = x

); its velocity vector is denoted

∂χ

∂x



∂u

∂x

,...,

∂u

∂x



If p = χ



,...,x



we will write χ

(p) rather than the more accurate



,..., x



and adopt the usual custom of picturing χ

(p) with its tail

at p in R

(Figure 4.3.6). The χ

are called coordinate velocity vectors corre-

sponding to χ. Being columns of the Jacobian these are linearly independent

at each p ∈ χ(U ) and so span an n-dimensional linear subspace of R

called

the tangent space to M at p and denoted

(M) = Span {χ

(p),...,χ

(p)}.



−1

( p)



( p)



( p)

(U )



M ⊆ IR

Fig. 4.3.6

To see that the subspace T

(M) does not depend on the particular coordinate

patch χ with which it is deﬁned we will obtain a more intrinsic description

of it. Let α : I → M be a smooth curve in M that passes through p at

t = t

(α(t

)=p). By continuity of α thereissomesubintervalJ of I

containing t

which α maps entirely into the image χ(U) of the coordinate

patch χ.Thenχ

−1

◦α is a smooth curve t → (x

(t),...,x

(t)) in U so α can

be written

α(t)=χ(x

(t),...,x

(t)),t∈ J.

By the chain rule,



)χ

(p). (4.3.16)

Thus, the velocity vector to every smooth curve in M through p is in T

(M).

4.3 Mathematical Machinery 219

Exercise 4.3.9 Show that, conversely, every nontrivial linear combina-

tion of χ

(p),...,χ

(p) is the velocity vector of some smooth curve in M

through p.

Thus, T

(M) can be identiﬁed with the set of velocity vectors to smooth

curves in M through p (together with the zero vector which one can think

of as the velocity vector to the, admittedly nonsmooth, constant curve in

M through p). In particular, the coordinate velocity vectors for any other

coordinate patch

˜χ :

U −→ M

with p ∈ ˜χ(

U) lie in T

(M) and so span the same subspace of R

Exercise 4.3.10 Let x

,...,x

and ˜x

,...,˜x

denote the coordinates in U

and

U, respectively, and χ : U → M and ˜χ :

U → M coordinate patches

with χ(U) ∩ ˜χ(

U) = ∅.Thenonχ

−1

(χ(U) ∩ ˜χ(

U)) the map ˜χ

−1

◦χ gives

˜x

,...,˜x

as functions of x

,...,x

˜x

=˜x

,...,x

),i=1,...,n,

and

χ(x

,...,x

)=˜χ(˜x

,...,x

),...,˜x

,...,x

)).

Show that, at each point of χ

−1

(χ(U) ∩ ˜χ(

U)),

∂˜x

∂x

˜χ

,i=1,...,n.

Show, moreover, that if p ∈ χ(U ) ∩ ˜χ(

U)andv ∈ T

(M)withv = v

(p)

and v =˜v

˜χ

(p), then

˜v

∂˜x

∂x

(χ

−1

(p))v

,j=1,...,n.

The elements of T

(M) are called tangent vectors to M at p.

Since we have determined that the event world is “locally like M”ateach

of its points we elect to model it by a smooth 4-manifold whose tangent spaces

are all provided with the structure of Minkowski spacetime, i.e., a Lorentz

inner product. A smooth assignment of an inner product to each tangent

space of a manifold is called a “metric” on M (not to be confused with the

term used in topology for a “distance function”, although there are some

connections). More precisely, a metric (or metric tensor) g on a manifold M

is an assignment to each tangent space T

(M),p∈ M , of an inner product

=  , 

such that the component functions g

deﬁned by

,...,x

)=g

(χ

(p),χ

(p)) = χ

(p),χ

(p)

are smooth on U for each coordinate patch χ : U → M . If each inner

product g

has index zero, g is called a Riemannian metric on M ;ifeach

220 4 Prologue and Epilogue: The de Sitter Universe

has index 1, then g is a Lorentzian (or Lorentz ) metric.Aspacetime is

a smooth 4-manifold on which is deﬁned a Lorentzian metric. In Euclidean

space R

, for example, one can take the identity map χ =id

as a global

chart so that χ

,...,χ

are constant and equal to the standard basis vectors

,...,e

for R

.EachT

) can therefore be identiﬁed with R

and one

can deﬁne a Riemannian metric g on R

by simply taking g

=  ,  for

each p ∈ R

.Theng

(p)=δ

,i,j =1,...,n,foreachp.OnR

one can

deﬁne a Lorentzian metric g by specifying that the inner product g

on each

)=R

satisﬁes g

(χ

(p),χ

(p)) = g

)=η

,i,j =1, 2, 3, 4. The

resulting spacetime is often denoted R

3,1

although, morally at least, it is just

Minkowski spacetime M.

Exercise 4.3.11 Suppose M is a manifold and g is a metric deﬁned on

M.Letχ : U → M and ˜χ :

U → M be coordinate patches for M with

χ(U) ∩ ˜χ(

U) = ∅ and with coordinates x

,...,x

on U and ˜x

,...,˜x

Show that

˜g

∂x

∂˜x

∂x

∂˜x

,i,j=1,...,n.

and conclude that, if the g

are smooth, then so are the ˜g

. Thus, at any

point it is enough to check smoothness in a single coordinate patch.

The examples of interest to us here (but certainly not all interesting ex-

amples) arise in a very simple way. If M is an n-manifold in R

, then one

can endow R

with various inner products and simply “restrict” these to

each T

(M). We will illustrate the idea ﬁrst for S

⊆ R

Consider a spherical coordinate parametrization

χ(φ, θ)=(sinφ cos θ, sin φ sin θ, cos φ)

of S

= φ, x

= θ). The coordinate velocity vectors (columns of the

Jacobian) are

= χ

=(cosφ cos θ, cos φ sin θ, −sin φ)

and

= χ

=(−sin φ sin θ, sin φ cos θ, 0).

At each point in the image of χ these are tangent vectors which we can regard

as vectors in R

and compute the R

-inner products

χ

,χ

 =cos

φ cos

θ +cos

φ sin

θ +sin

φ =1

χ

,χ

 =sin

φ sin

θ +sin

φ cos

θ =sin

χ

,χ

 = χ

,χ

 =0.

Thus, if we deﬁne a (Riemannian) metric g on S

by taking g

(v, w)=v, w

for each p ∈ S

and all v, w ∈ T

) ⊆ R

the components g

,i,j=1, 2,

are given by

4.3 Mathematical Machinery 221







0sin



(4.3.17)

and these are certainly smooth.

Exercise 4.3.12 Deﬁne a Riemannian metric on S

by restricting the usual

Euclidean inner product  ,  on R

to each T

),p∈ S

. Show that the

metric components g

,i,j=1, 2, 3, relative to the spherical coordinates

= φ

= θ given by (4.3.9)are

⎛

⎝

⎞

⎠

⎛

⎝

10 0

0sin

00sin

sin

⎞

⎠

To obtain examples of Lorentz metrics in this way we will need to be-

gin with an inner product of index one on some R

to restrict to a man-

ifold M ⊆ R

. This can be done in any dimension, but we will restrict

our attention to the one example we would like to understand, that is, the

de Sitter spacetime. For this we begin with the 5-dimensional analogue of

Minkowski spacetime. Speciﬁcally, on R

with standard coordinate functions

,...,u

we introduce an inner product denoted ( , ) and deﬁned by

(p, q)=((p

,...,p

), (q

,...,q

))

= p

+ ···+ p

− p

= η

where

⎧

⎪

⎨

⎪

⎩

1 ,i= j =1, 2, 3, 4

−1 ,i= j =5

0 ,i= j

(using η for this as well as the corresponding matrix for M should lead to no

confusion since the context will always indicate which is intended). We will

denote by M

the real vector space R

with this inner product. Notice that

the manifold D in R

is just the set of points p in M

with

(p, p)=1.

We now appropriate for M

all of the basic terminology and notation in-

troduced for Minkowski spacetime, e.g., v ∈M

is spacelike if (v, v) > 0,

timelike if (v, v) < 0andnull if (v, v)=0,thenull cone C

)atany

∈M

is the set C

)={x ∈M

:(x −x

,x−x

)=0},thetime cone

at x

is C

)={x ∈M

:(x − x

,x− x

) < 0},andsoon.Indeed,allof

the basic geometry of M is completely insensitive to the number of “spatial

dimensions” and so generalizes immediately to M

. Use the following few

exercises as an opportunity to persuade yourself that this is true.

222 4 Prologue and Epilogue: The de Sitter Universe

Exercise 4.3.13 Prove that two nonzero null vectors v and w in M

are

orthogonal if and only if they are parallel.

Exercise 4.3.14 Let {e

,...,e

} be any orthonormal basis for M

((e

)=η

). Show that if v = v

is timelike and w = w

is either

timelike or null and nonzero, then either

(a) v

> 0, in which case (v,w) < 0, or

(b) v

< 0, in which case (v,w) > 0.

With this last exercise one can introduce time orientations (future-directed

and past-directed ) for timelike and nonzero null vectors in M

in precisely

the same way as it was done in Minkowski spacetime (Section 1.3).

Exercise 4.3.15 Prove that the sum of any ﬁnite number of vectors in M

all of which are timelike or null and all future-directed (resp., past-directed)

is timelike and future-directed (resp., past-directed) except when all of the

vectors are null and parallel, in which case the sum is null and future-directed

(resp., past-directed).

The causality relations  and < are deﬁned on M

just as they are on

M (x  y ⇐⇒ y −x is timelike and future-directed and x<y⇐⇒ y − x is

null and future-directed) and all of their basic properties are proved in the

same way.

Exercise 4.3.16 Show that, for distinct points x and y in M

x<y if and only if

)

y and

y z =⇒ x  z

An orthogonal transformation of M

is a linear transformation L : M

→

. satisfying (Lx , Ly)=(x, y) for all x, y ∈M

and these have matri-

ces Λ =





i,j=1,2,3,4,5

relative to orthonormal bases deﬁned exactly as in

M (Section 1.2) which satisfy Λ

ηΛ=η,whereη =(η

)

i,j=1,2,3,4,5

.Those

which satisfy, in addition, Λ

≥ 1 are called orthochronous and these pre-

serve the time orientation of all timelike and nonzero null vectors and so pre-

serve the causality relations (x  y ⇐⇒ Lx  Ly and x<y⇐⇒ Lx < Ly).

Just as in M, Λ

ηΛ=η implies det Λ = ±1 and we single out those with

det Λ = 1 to refer to as proper. The collection

Λ=





i,j=1,2,3,4,5

:Λ

ηΛ=η, Λ

≥ 1, det Λ = 1

is the analogue in M

of the proper, orthochronous Lorentz group L.

And so the story goes. Essentially everything purely geometrical that we

have said about M and L is equally true of M

and L

. Indeed, even

Zeeman’s Theorem 1.6.2 remains true for M

. More precisely, a bijection

F : M

→M

satisfying x<yif and only if F (x) <F(y) (or, equivalently,

4.3 Mathematical Machinery 223

x  y if and only if F (x)  F(y)) is called a causal automorphism and one

proves, essentially as in Section 1.6, that any such is the composition of an

orthochronous orthogonal transformation of M

, a translation of M

and

a dilation of M

. We will not belabor this point any further here, but will

simply leave it to the skeptical reader to check that when we need a result

proved for M to be true in M

,itis.

Of course, something is lost in moving from M to M

and that is the

physical interpretation (the event world is, to the best of our knowledge,

4-dimensional, not 5-dimensional). To return to physics we must return to

D⊆M

Our intention is to do for D⊆M

what we did for S

⊆ R

and S

⊆ R

that is, restrict the inner product of the ambient space to each tangent space

of the manifold, thereby deﬁning a metric.

Remark: The fact that we actually get a metric in this way is not as obvious

as it was in the positive deﬁnite case. The restriction of ( , ) to each T

(D)

is surely bilinear and symmetric, but is not obviously nondegenerate nor is

it obviously of index one. That it is, in fact, nondegenerate and of index one

will follow from the calculations we are about to perform.

We will describe the metric components ﬁrst in global coordinates (x

= φ

= θ, x

= t

). The coordinate velocity vectors are, from

Example 4.3.2,

= χ

=(cosht

cos φ

, cosh t

cos φ

sin φ

cos θ,

cosh t

cos φ

sin φ

sin θ, −cosh t

sin φ

, 0)

= χ

=(−cosh t

sin φ

, cosh t

sin φ

cos φ

cos θ,

cosh t

sin φ

cos φ

sin θ, 0, 0)

= χ

=(0, −cosh t

sin φ

sin θ,

cosh t

sin φ

cos θ, 0, 0)

= χ

=(sinht

sin φ

cos φ

, sinh t

sin φ

cos θ,

sinh t

sin φ

sin θ, sinh t

cos φ

, cosh t

Thus, for example,

=(χ

,χ

)=cosh

cos

+cosh

cos

sin

cos

+cosh

cos

sin

θ +cosh

sin

− 0

=cosh

[cos

cos

+cos

sin

+sin

]

=cosh

=(χ

,χ

)=sinh

sin

cos

+sinh

sin

cos

+sinh

sin

θ +sinh

cos

− cosh