Naber G.L. The Geometry of Minkowski Spacetime. An Introduction to the Mathematics of the Special Theory of Relativity

Подождите немного. Документ загружается.

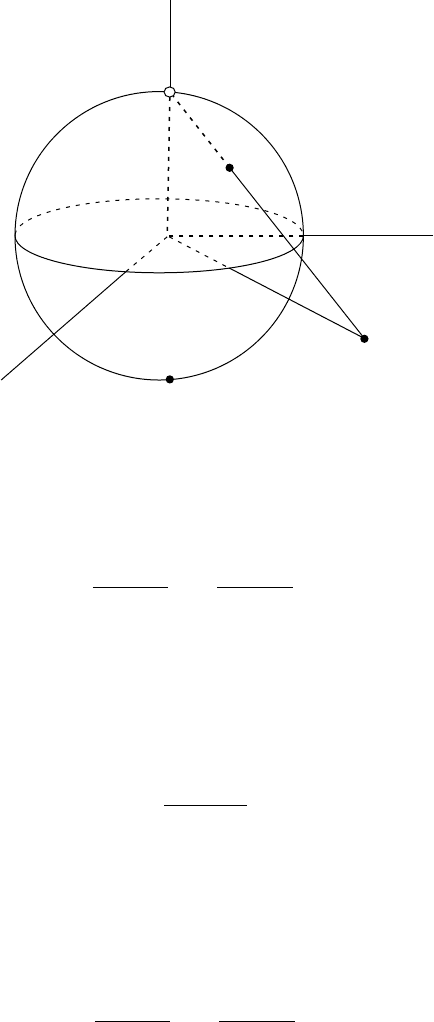
204 4 Prologue and Epilogue: The de Sitter Universe

(p)

Fig. 4.3.1

A simple computation gives

(p)=ϕ

,...,p

n+1

) (4.3.1)



1 − p

n+1

,...,

1 − p

n+1



=(x

,...,x

Notice that ϕ

is clearly smooth on U

. It is, in fact, a bijection onto R

since it is a simple matter to check that its inverse

−1

: R

−→ U

is given by

−1

(x)=ϕ

−1

,...,x

1+  x 

(2x

,...,2x

,  x 

−1). (4.3.2)

Since ϕ

−1

is clearly also smooth we ﬁnd that ϕ

is a diﬀeomorphism of U

onto R

and so ϕ

−1

is a diﬀeomorphism of R

onto U

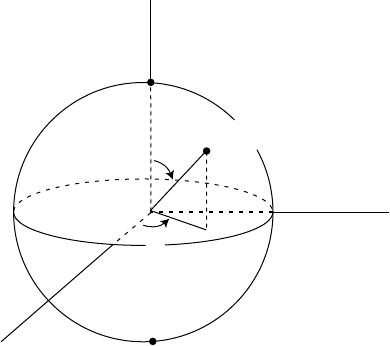
Similarly, for each p ∈ U

,ϕ

(p) is the intersection with u

n+1

=0ofthe

straight line in R

n+1

from S through p (see Figure 4.3.2). One ﬁnds that

(p)=ϕ

,...,p

n+1

) (4.3.3)



1+p

n+1

,...,

1+p

n+1



=(y

,...,y

)

4.3 Mathematical Machinery 205

(p)

Fig. 4.3.2

which is a smooth bijection with inverse

−1

: R

−→ U

given by

−1

(y)=ϕ

−1

,...,y

1+  y 

(2y

,...,2y

, 1−y 

) (4.3.4)

and this is also smooth. Consequently, ϕ

: U

→ R

and ϕ

−1

: R

→ U

are also inverse diﬀeomorphisms.

We think of the diﬀeomorphism ϕ

as identifying U

with R

and thereby

supplying the points of U

with n coordinates, called (x

,...,x

)above.

Similarly, ϕ

provides points in U

with n coordinates (y

,...,y

). Notice

that a point p in U

∩ U

= S

−{N, S} is therefore supplied with two sets of

coordinates. These are related by the coordinate transformations ϕ

◦ ϕ

−1

∩ U

) → ϕ

∩ U

)andϕ

◦ ϕ

−1

: ϕ

∩ U

) → ϕ

∩

). But

∩ U

)=ϕ

∩U

)=R

−{(0,...,0)}

and it is easy to check that

◦ ϕ

−1

(x)=ϕ

◦ ϕ

−1

,...,x

 x 

,...,x

) (4.3.5)

206 4 Prologue and Epilogue: The de Sitter Universe

and

◦ ϕ

−1

(y)=ϕ

◦ ϕ

−1

,...,y

 y 

,...,y

). (4.3.6)

The essential content of all this is that S

is “locally diﬀeomorphic to R

”

in the sense that each point of S

is contained in an open subset of S

that

is diﬀeomorphic to R

. This is the prototype for our next deﬁnition.

Let n and m be positive integers with n ≤ m. A subset M of R

is called

an n-dimensional smooth manifold (or smooth n-manifold) if, for each p ∈ M,

there is an open set U in M containing p and a diﬀeomorphism ϕ : U → ϕ(U)

of U onto an open subset ϕ(U)ofR

.Thus,S

is an n-dimensional smooth

manifold in R

n+1

Remark: There is a more general deﬁnition of “smooth manifold” that does

not require M to be a subset of a Euclidean space (see Chapter 5 of [N

]),

but this will suﬃce for our purposes.

Exercise 4.3.1 Show that every open ball in R

is diﬀeomorphic to R

and

conclude that every point in a smooth n-manifold M iscontainedinanopen

subset of M that is diﬀeomorphic to all of R

The pair (U, ϕ) is called a chart on M .Asmoothn-manifold is just a subset

M of some Euclidean space for which there exists a family {(U

,ϕ

):α ∈A}

of charts

: U

−→ ϕ

) ⊆ R

with

α∈A

= M .Eachϕ

supplies the points of U

with n coordinates,

namely, those of its image in ϕ

). If U

∩U

= ∅,thenapointp ∈ U

∩U

is supplied with two sets of coordinates, say,

(p)=(x

,...,x

)

and

(p)=(y

,...,y

These are related by the transformation equations

◦ ϕ

−1

: ϕ

∩ U

) −→ ϕ

∩ U

)

,...,x



◦ ϕ

−1



,...,y

)

and

◦ ϕ

−1

: ϕ

∩U

) −→ ϕ

∩ U

)

,...,y



◦ ϕ

−1



,...,x

is itself a smooth n-manifold with a global chart (R

, id

). The corre-

sponding coordinates are just the standard coordinates u

,...,u

.Thesame

4.3 Mathematical Machinery 207

is true of any open subset of R

. To produce more interesting examples we

will need to develop a technique for manufacturing charts. One particularly

simple case is contained in the following exercise.

Exercise 4.3.2 Let V be an open set in R

and g : V → R asmooth

real-valued function on V . Show that the graph {(x, g(x)) : x ∈ V } of g in

n+1

= R

× R is a smooth n-manifold with a global chart.

The sphere S

is not the graph of a function of n variables, but it can

be covered by open sets each of which is the graph of a function, e.g., the

hemispheres with u

> 0andu

< 0fori =1,...,n+ 1. These functions

“parametrize” the hemispheres of S

and the projections back onto the do-

mains provide charts. There are, however, many other ways of parametrizing

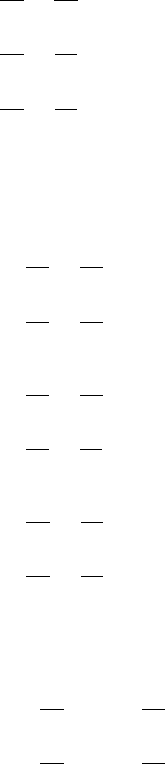
regions on the sphere. For example, the map

χ :[0,π] × [0, 2π] −→ R

deﬁned by

χ(φ, θ)=(sinφ cos θ, sin φ sin θ, cos φ) (4.3.7)

maps into (in fact, onto) the 2-sphere S

in R

and parametrizes S

standard spherical coordinates. The geometrical interpretation of φ and θ is

( sin f cos q, sin f sin q, cos f )

Fig. 4.3.3

the usual one from calculus (see Figure 4.3.3). Notice that χ is one-to-one on

(0,π) × (0, 2π)andcoversallofS

except the north and south poles and

the longitudinal curve at θ =0(orθ =2π) joining them. On this open set

in S

,χhas an inverse and this has a chance of being a chart. In this case

one can actually calculate this inverse explicitly and show that it is, indeed,

smooth and therefore a chart. To obtain a chart covering the longitudinal

208 4 Prologue and Epilogue: The de Sitter Universe

curve joining the north and south poles (but not N and S themselves) one

canusethesamemapχ, but on the open set (0,π) × (−π, π). To cover N

and S themselves one simply deﬁnes an analogous map, but measuring the

angle φ from a diﬀerent axis. It is customary to be a bit sloppy and refer to

all of these collectively as “spherical coordinates” on S

We would like to apply this same idea in much more generality. Given

a subset M of R

we will ﬁnd parametrizations of regions in M and hope

to “invert” them to obtain charts. More often than not, however, such in-

verses are diﬃcult or impossible to compute explicitly. Fortunately, there is a

remarkable result from real analysis that can often relieve one of the responsi-

bility of doing this. We will now state this result in the form most convenient

for our purposes and refer to [Sp1] for details.

If U is an open set in R

and F : U → R

is a smooth map we will write

F =(F

,...,F

) for the coordinate functions of F, D

for the j

partial

derivative of F

and, for each a ∈ U, the Jacobian of F at a will be written



(a)=(D

(a))

1 ≤ i ≤ m

1 ≤ j ≤ n

⎛

⎜

⎝

(a) ··· D

(a)

(a) ···D

(a)

⎞

⎟

⎠

The Inverse Function Theorem applies to the special case in which m = n

and says that when the Jacobian F



(a) is nonsingular, then F is a local

diﬀeomorphism near a. More precisely, we have

The Inverse Function Theorem: Let U be an open subset of R

and

F : U → R

a smooth map. Suppose a ∈ U and F



(a) is nonsingular (i.e.,

detF



(a) =0). Then there exist open sets V and W in R

with a ∈ V ⊆ U

and F (a) ∈ W ⊆ R

such that the restriction of F to V

F | V : V −→ W

is a diﬀeomorphism onto W, i.e., a smooth bijection with a smooth inverse

(F | V )

−1

: W −→ V.

Moreover,



(F | V )

−1





(F (a)) = (F | V )



(a) .

Now let us suppose that we did not wish to go to the trouble of inverting

the spherical coordinate parametrization

χ :(0,π) × (0, 2π) −→ R

χ(φ, θ)=(sinφ cos θ, sin φ sin θ, cos φ)

explicitly on its image in S

. We would like to use the Inverse Function

Theorem to conclude nevertheless that it provides a chart at each point in

the image. Let’s write χ in more familiar notation as

4.3 Mathematical Machinery 209

x =sinφ cos θ

y =sinφ sin θ. (4.3.8)

z =cosφ

Then the Jacobian of χ is given by



(φ, θ)=

⎛

⎜

⎝

∂x

∂φ

∂x

∂θ

∂y

∂φ

∂y

∂θ

∂z

∂φ

∂z

∂θ

⎞

⎟

⎠

⎛

⎜

⎝

cos φ cos θ −sin φ sin θ

cos φ sin θ sin φ cos θ

−sin φ 0

⎞

⎟

⎠

We claim that, at each (φ, θ) ∈ (0,π) ×(0, 2π),χ



(φ, θ) has maximal rank

(namely, 2). To see this we compute the determinants of the various 2 × 2

submatrices.



∂x

∂φ

∂x

∂θ

∂y

∂φ

∂y

∂θ



=cosφ sin φ



∂x

∂φ

∂x

∂θ

∂z

∂φ

∂z

∂θ



= −sin

φ sin θ



∂y

∂φ

∂y

∂θ

∂z

∂φ

∂z

∂θ



=sin

φ cos θ

For φ ∈ (0,π), sin φ = 0 so, for any (φ, θ) ∈ (0,π) × (0, 2π), at least one

of these is nonzero. Let’s suppose we are at a point a =(φ

,θ

)atwhich



∂x

∂φ

(a)

∂x

∂θ

(a)

∂y

∂φ

(a)

∂y

∂θ

(a)



=0

(the other cases are treated in the same way). Deﬁne an open set

U =(0,π) × (0, 2π) × R

210 4 Prologue and Epilogue: The de Sitter Universe

in R

and extend χ to a smooth map

˜χ :

U −→ R

˜χ(φ, θ, t)=(x(φ, θ),y(φ, θ),z(φ, θ)+t)

=(sinφ cos θ, sin φ sin θ, cos φ + t).

The Jacobian of ˜χ is

⎛

⎜

⎝

∂x

∂φ

∂x

∂θ

∂y

∂φ

∂y

∂θ

∂z

∂φ

∂z

∂θ

⎞

⎟

⎠

and this is nonsingular at (a, 0) = (φ

,θ

, 0) ∈ R

.Since˜χ(a, 0) = χ(a),

the Inverse Function Theorem implies that there are open sets V and W in

with (a, 0) ∈ V ⊆

U and χ(a) ∈ W ⊆ R

such that ˜χ|V : V → W is

a diﬀeomorphism. The restriction of this diﬀeomorphism to V ∩ ((0,π) ×

(0, 2π) ×{0}) is therefore a diﬀeomorphism of an open set in (0,π) ×(0, 2π)

(identiﬁed with (0,π) × (0, 2π) ×{0}) containing a onto the intersection of

the image of χ :(0,π) × (0, 2π) → R

with W . But this intersection is an

open set in S

containing χ(a) so the inverse of this last diﬀeomorphism is a

chart for S

at χ(a).

The bottom line here is this. The smooth parametrization (4.3.8)has

xim

al rank at each point of (0,π) × (0, 2π) and from this alone the

Inverse Function Theorem implies that it can be smoothly inverted on an

open set about any point in (0,π) × (0, 2π), thus providing a chart in S

near the image of that point. This is a very powerful technique that we will

use repeatedly, but one should not get carried away. Had we not known in

advance that χ :(0,π) × (0, 2π) → R

is one-to-one, this would in no way

follow from what we have done with the Inverse Function Theorem, which

guarantees invertibility only near a point where the Jacobian is nonsingular.

Of course, since we do know that χ is one-to-one on (0,π)×(0, 2π) our argu-

ments show that its inverse is smooth (a map on S

is smooth, by deﬁnition,

if it is smooth on some open set about each point).

In order to avoid repeating the same argument over and over again we

will now prove a general result that can be applied whenever we need to

manufacture a chart. Thus, let us suppose that M is a subset of some R

is an open set in R

,wheren ≤ m,and

χ : U −→ R

4.3 Mathematical Machinery 211

is a smooth map with χ(U ) ⊆ M .Writex

,...,x

for the standard

coordinates on R

and χ

,...,χ

for the coordinate functions of χ.

Suppose a ∈ U is a point at which the Jacobian χ



(a)hasrankn.Thensome

n ×n submatrix of χ



(a) is nonsingular and, by renumbering the coordinates

if necessary, we may assume that

⎛

⎜

⎝

(a) ··· D

(a)

(a) ··· D

(a)

⎞

⎟

⎠

∂(χ

,...,χ

)

∂(x

,...,x

)

(a)

is nonsingular. If m = n, then the Inverse Function Theorem implies that χ

gives a chart at χ(a). Now assume n<m, deﬁne

U = U × R

m−n

and let

˜χ :

U −→ R

be deﬁned by

˜χ(x, t)= ˜χ(x

,...,x

,...,t

m−n

)

=(χ

(x),...,χ

(x),χ

n+1

(x)+t

,...,χ

(x)+t

m−n

Then ˜χ is smooth and its Jacobian at (a, 0) is

⎛

⎜

⎝

∂(χ

,...,χ

)

∂(x

,...,x

)

(a)O

∂(χ

n+1

,...,χ

)

∂(x

,...,x

)

(a)I

⎞

⎟

⎠

where O is the n × (m − n) zero matrix and I is the (m − n) × (m − n)

identity matrix. This is nonsingular so the Inverse Function Theorem implies

that there exist open sets V and W in R

with (a, 0) ∈ V ⊆

U and ˜χ(a, 0) =

χ(a) ∈ W ⊆ R

such that ˜χ|V : V → W is a diﬀeomorphism. The restriction

of this diﬀeomorphism to V ∩ (U ×{0}) is therefore a diﬀeomorphism of an

open set in U (identiﬁed with U ×{0}) containing a onto the intersection of

the image of χ : U → R

with W . But this intersection is an open set in M

containing χ(a) so the inverse of this last diﬀeomorphism is a chart for M

at χ(a). We will refer to a smooth map χ : U → M ⊆ R

,whereU is open

in R

and χ



(a) is nonsingular for each a in U,asacoordinate patch for M .

Thus, each point in the image χ(U ) ⊆ M iscontainedinanopensubsetof

M on which χ

−1

is a chart for M.

We will have occasion to use a great variety of charts (i.e., coordinate

systems) on the manifolds of interest to us so we will pause now to write out

some of these.

Example 4.3.1 We begin with a simple, but useful generalization of the

spherical coordinate parametrization of S

. We deﬁne a map

χ :[0,π] × [0,π] × [0, 2π] −→ R

212 4 Prologue and Epilogue: The de Sitter Universe

χ(φ

,φ

,θ)=(sin φ

cos φ

, sin φ

sin φ

cos θ, sin φ

sin φ

sin θ, cos φ

Thus,

=sinφ

cos φ

=sinφ

sin φ

cos θ

=sinφ

sin φ

sin θ (4.3.9)

=cosφ

A little trigonometry shows that (u

)

+(u

)

+(u

)

+(u

)

=1soχ maps

into (in fact, onto) S

. The Jacobian is

⎛

⎜

⎝

cos φ

−sin φ

sin φ

cos φ

sin φ

cos θ sin φ

cos φ

cos θ −sin φ

sin φ

sin θ

cos φ

sin φ

sin θ sin φ

cos φ

sin θ sin φ

sin φ

cos θ

−sin φ

⎞

⎟

⎠

Computing the determinants of all of the 3 × 3 submatrices we obtain

sin

cos φ

sin φ

− sin

sin

sin θ

sin

cos θ

− sin

sin φ

cos φ

Note that φ

=0givesthepointN =(0, 0, 0, 1) and φ

= π gives S =

(0, 0, 0, −1) and that all of the 3 × 3 determinants vanish at these points.

These determinants also vanish when φ

=0andφ

= π.For(φ

,φ

) ∈

(0,π) ×(0,π) one of the second or third determinants above is nonzero. We

conclude, in particular, that each point of (0,π)×(0,π)×(0, 2π)iscontained

in an open set on which χ is a diﬀeomorphism onto an open set in S

and the

inverseofthisisachartonS

with coordinate functions (φ

,φ

,θ). As for

one obtains charts at the remaining points of S

by either replacing (0, 2π)

with (−π, π) or interchanging the roles of some of the standard coordinates

on R

and these charts are collectively called spherical (or hyper-spherical)

coordinates on S

. An obvious modiﬁcation provides, for any ρ>0, spherical

coordinates

= ρ sin φ

cos φ

= ρ sin φ

sin φ

cos θ

= ρ sin φ

sin φ

sin θ (4.3.10)

= ρ cos φ

4.3 Mathematical Machinery 213

on the sphere

)

+(u

)

+(u

)

+(u

)

= ρ

of radius ρ in R

Exercise 4.3.3 Show that, for ρ>0andforφ

,φ

and θ exactly as in the

case of S

,(4.3.10) determines a chart at each point of R

except the origin.

Next we turn to the manifold that will occupy most of our time. It is a 4-

dimensional manifold in R

and upon it we will build the de Sitter universe.

Various diﬀerent coordinate systems on it elucidate diﬀerent aspects of its

geometrical and physical structure so we will spend some time introducing a

number of them.

We consider the subset D of R

given in terms of standard coordinates

)

+(u

)

+(u

)

+(u

)

− (u

)

=1.

Notice that the intersection of D with u

=0isjustS

and, more generally,

setting u

equal to some constant value u

gives a slice of D that is just a

3-sphere of radius



1+(u

)

Exercise 4.3.4 Show that, in fact, D is diﬀeomorphic to S

× R. Hint:

Consider the map F : D→S

× R given by

F (u





1+(u

)



−



1+(u

)



−



1+(u

)



−



1+(u

)



−



By virtue of the analogy between D and x

+ y

−z

=1inR

we picture D

as a “hyperboloid” in R

whose cross-sections at constant u

are 3-spheres

rather than circles (see Figure 4.3.4).

mple 4

.3.2 Our ﬁrst parametrization of D is the most natural one in

light of this picture. We view D as a family of 3-spheres, one for each −∞ <

< ∞, with radii evolving hyperbolically and each such sphere parametrized

as in (4.3.10). Speciﬁcally, we deﬁne

=cosht

sin φ

cos φ

=cosht

sin φ

cos θ

=cosht

sin φ

sin θ (4.3.11)

=cosht

cos φ

=sinht