Mrinal K Pal. Power system stability
Подождите немного. Документ загружается.


VOLTAGE STABILITY
10-33
The limit shown on Figure 10.19 as point B, the point at which the load characteristic b is
tangent to the system PV curve, is therefore also the voltage stability limit. It follows that the
equilibrium point A is stable and A′ is unstable.
Problem
Referring to Figure 10.16, assume that the load is purely reactive and that the entire load is
supplied locally by switched shunt capacitors so that there is no reactive flow on the transmission
line, i.e.,
SR
VV = . What would be the maximum load that can be supplied if the load is constant
power. (Answer:
X
V
Q
S
2
2
lim
= )
Extension to large networks
The above result can be readily extended to large networks if we first relate the stability limit, as
determined above, to the power flow Jacobian, modified to reflect the static part of the load.
For the simple example considered above, the incremental power flow equations can be written
as
∆
∆
−
−
−−
=
∆
∆
V
X
V
X
BXV
X
VV
X
V
GV
X
VV
Q
P
S
L
LS
S
LL
LS
θ
θθ
θθ
cos
)1(2
sin
sin2cos
Note that the conventional power flow Jacobian has been augmented by terms arising from the
resistive part of the load.
We now determine the singularity condition of this modified Jacobian. The Jacobian is singular
when the determinant is zero. After evaluating the determinant and carrying out the necessary
algebraic manipulations, the condition for singularity is obtained as
P
GV
LL
2
2cos −=
θ
which is the same as the condition for voltage stability limit. Therefore, the voltage stability
limit, when the load contains static components, is indicated by the singularity of the modified
Jacobian.
The extension to large networks follows directly from the above analysis. Power flow equations
are first written, separating the voltage dependent part of the load from the constant power part,
as shown in (10.56) and (10.57).
),()( VθfVPP
=
+ (10.56)
),()( VθgVQQ
=
+ (10.57)
The linearized power flow equations are written as follows:
∆
∆
′
′
=
∆
∆
V
θ
JJ
JJ
Q
P
QVQ
PVP
θ
θ
(10.58)
where

VOLTAGE STABILITY
10-34
V
VQ
JJ
V
VP
JJ
∂
∂
−=
′
∂
∂
−=
′
)(
)(
QVQV
PVPV
At the generator and other voltage controlled buses ∆V’s are zero, so that the Jacobian would be
adjusted, as is customary in a power flow solution under perfect voltage control. It is important
to account for any nonconformity of the voltage controlled buses. For example, when any of the
generators reaches excitation limit, its terminal voltage is no longer constant. Instead, the
constant voltage under fixed excitation is the voltage behind synchronous reactance (the field
voltage), as noted earlier. This should be reflected in the Jacobian.
Large disturbance voltage stability for mixed loads
It has been shown that when a part of the total load is static, voltage stability limit can extend
beyond the maximum power point on the system PV curve. For such loads stability can be
maintained for initial pre-disturbance load greater than the maximum power capability of the
post-disturbance system. This is because a stable equilibrium point may be possible in the post-
disturbance system, although the actual power delivered will be reduced following the
disturbance.
In order to illustrate this further, consider the case when about 50% of the load is resistive. The
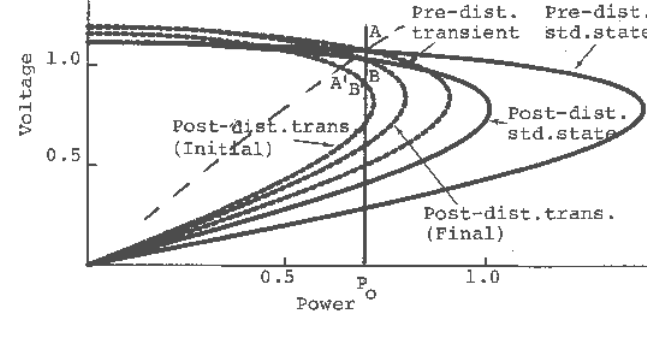
system PV curves and the steady-state load characteristics for this case are shown in Figure
10.20, in solid lines. For a total load P
1
, A is the initial, pre-disturbance, operating point. The
equilibrium points following the disturbance are shown on the post-disturbance PV curve at B
and B′. (Recall that when a part of the load is static, both equilibrium points can be on the lower
portion of the system PV curve.)
Fig. 10.20 System PV curves and steady-state (solid lines) and instantaneous (dashed lines) load
characteristics when part of the load is static.
Using a similar argument as before, it can be concluded that the region to the right of B′ (the
unstable equilibrium point) is the region of attraction of the stable equilibrium point B.
Following a disturbance the operating point moves to A′, the intersection of the post-disturbance
PV curve and the instantaneous load characteristic, shown by the dashed line a′. Since it is within
the region of attraction of the stable equilibrium point B, the system will be stable. The
approximate path of the operating point from initial to final state is marked by arrows as shown.
VOLTAGE STABILITY
10-35
Note that if the initial total load is P
2
, an equilibrium point would not exist in the post-
disturbance system, and voltage instability would occur following the disturbance. Once again
we can conclude that large disturbance voltage stability is assured by the existence of a stable
equilibrium point in the post-disturbance system.
Voltage stability for fast response load
In the voltage stability analyses for constant MVA loads presented so far, it was assumed that the
mechanisms that restore the loads to constant MVA act much slower compared to the
mechanisms that restore system voltages, which are primarily the generator voltage controls. In
many power systems this assumption may be unrealistic. When the load response speed is
comparable to the speed of response of the voltage control devices, the assumption of constant
system voltage can introduce considerable error.
A conceptual understanding of the issues involved in the voltage stability for such loads may be
obtained through the use of “transient” system PV curves. Figure 10.21 shows the steady-state
and transient PV curves when the load power is P
0
. The transient curves, shown by dashed lines,
were obtained using a fictitious voltage, held constant during the transient period, behind a
fictitious reactance. In practice, it may not be a simple matter to estimate the correct value of this
reactance. The present purpose is to provide a conceptual understanding of the issues involved
and, as such, the transient curves are hypothetical. For the load P
0
, the initial operating point is at
A, the intersection of the pre-disturbance steady-state PV curve, the transient PV curve and the
steady-state load characteristic, which is a vertical line at P
0
for the constant power load
assumed.
Fig. 10.21 Large disturbance voltage stability for fast response loads using “transient” PV
curves.
Following the disturbance the operating point first moves to A′, the intersection of the post-
disturbance transient PV curve and the instantaneous load characteristic. Since A′ is within the
region of attraction of the stable equilibrium point B′, on the transient PV curve, the system will
be transiently stable. The operating point will eventually settle at B, the intersection of the post-
disturbance steady-state and final transient PV curves and the steady-state load characteristic.
Figure 10.22 shows the case when the initial load is at a somewhat higher level, so that an
intersection between the steady-state load characteristic and the post-disturbance system transient
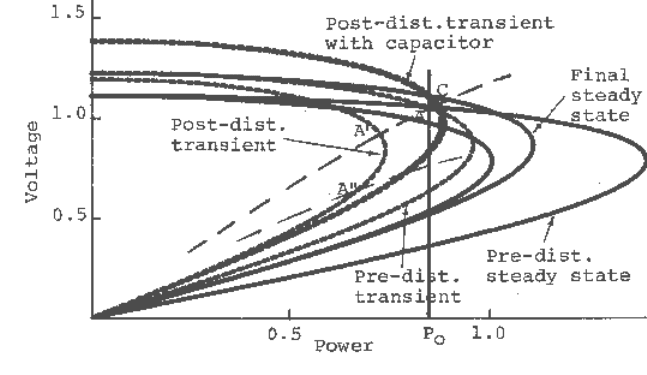
VOLTAGE STABILITY
10-36
PV curve does not exist. [A steady-state equilibrium point, however, exists in the post-
disturbance system, at the load level assumed.] It is evident that, without some sort of control
action, voltage instability would occur following the disturbance. With appropriate control
action, voltage stability can be maintained. For example, if sufficient capacitors are switched on
promptly, stable operation can be restored as illustrated in the figure. In the illustration, the
operating point first moves to A′ following the disturbance. It would then move down the
transient PV curve and, in the absence of any control action, voltage instability would follow.
With prompt capacitor switching, the system state can be brought within the region of attraction
of the stable equilibrium point on the new transient PV curve, so that it eventually moves to the
stable equilibrium point C. Note that if the capacitor switching is delayed so that the operating
point has moved beyond A″ on the transient PV curve, stable operation cannot be restored. This
is because the initial state following the capacitor insertion would fall outside the region of
attraction of the new stable equilibrium point. In some extreme situations it may be necessary to
resort to SVC’s in order to maintain stability.
Fig. 10.22 Illustration of voltage instability following a large disturbance for a fast response load.
The objective of the above discussion was to emphasize the need for a detailed analysis,
considering both small and large disturbances, when the bulk of the load is composed of fast
response loads and voltage stability may be in question. The analysis would require detailed
modeling of generators and their control equipment, particularly, the excitation controls. No
simple criterion can be employed in such situations. In non-critical situations, approximate
estimates of voltage stability limits for such loads may be obtained based on steady-state
analyses, using a constant generator internal voltage behind a conservatively estimated reactance,
in place of the constant generator terminal voltage as used in the conventional power flow model
Voltage Stability Using Static Load Models
In order to keep the algebra simple, the load will be assumed to be purely reactive. Also, for
simplicity, only the generator field flux dynamics is considered, and constant field voltage (manual
excitation control) is assumed. The generator equations, in simplified form and using standard
notations (see Chapter 5), are
qdddfdqdo
eixxEeT
′
−
′
−
−
=
′′
)(
&
(10.59)

VOLTAGE STABILITY
10-37
ddqq
ixee
′
+
=
′
(10.60)
qqd
ixe
−
=0
(10.61)
Referring to Figure (10.16), since the load is assumed to be purely reactive, from equation (10.42),
LL
b
L
L
L
IV
V
V
QQ =
=
0
0
(10.62)
where
BVII
LL
+
=
Also
IXVVeeiIi
LSqdqd
+
=
=
=== and0,0,
After linearizing equations (10.59) - (10.62) around the operating point, and eliminating the non-
state variables, the following equation is obtained:
q
ddL
ddL
qdo
e
bQXXBV
bQXBXV
eT
′
∆
−
′
+
′
−
−+−
−=
′
∆
′
)1()1(
)1()1(
0
2
0
2
&
(10.63)
where
dddd
xXXxXX
′
+
=
′
+= and
For normal values of B, 1)or(
<
<
′
dd
XBBX . Equation (10.63) shows that, for b = 1 or 2, operation
is always stable. This means that for static loads, such as constant impedance or constant current
loads, there cannot be voltage instability. For b = 0, equation (10.63) becomes
q
ddL
ddL
qdo
e
QXXBV
QXBXV
eT
′
∆
′
−
′
−
−−
−=
′
∆
′
0
2
0
2
)1(
)1(
&
which can be written as
q
dL
dL
qdo
e
XBB
XBB
eT
′
∆
′
+−
+
−
−=
′
∆
′
)(1
)(1
&
(10.64)
where B
L
is the equivalent admittance of the constant reactive power load (
LL
BVQ
2
0
= ).
Equation (10.64) shows that operation is stable for
dL
XBB )(
+
< 1 as well as for
dL
XBB
′
+ )(> 1,
and unstable for
dL
XBB )( + > 1 >
dL
XBB
′
+
)( . This means that, as the loading is increased from
zero, there will be a stable region, followed by an unstable region, then another stable region. This is
illustrated on the (reactive) power/voltage curve in Figure 10.23, drawn for constant generator
terminal voltage, held at unity by manual excitation control, and using the parameter values
,3.0,3.0,5.1 ==
′
= Xxx
dd
B = 0.

VOLTAGE STABILITY
10-38
Fig. 10.23 Stable and unstable regions as obtained from constant (reactive) power static load model.
Note that, according to this model of the constant (reactive) power load, the entire lower portion of
the power-voltage curve, drawn with respect to the generator terminal voltage is stable. This
conclusion will not change even if excitation and other control actions are included in the analysis.
For example, in Reference 20, voltage stability analysis using a detailed generator and control
system model, but static model for the constant power load has been reported. The analysis
identified the entire lower portion of the PV curve as stable. A consideration of the physical
behavior of a constant power load will show [21] that this is not possible. The cause of the anomaly,
which is due to the use of a static model to represent a dynamic element that determines the stability
behavior, should be evident from the above analysis. The analyses presented in subsequent sections
will confirm that, if a realistic model were employed for the constant power load, the second
stability region would not exist.
When the effect of the excitation control is included in the system model, the stability region will
extend considerably. The point at which instability sets in will depend on the dynamic response
speed of the constant power load. For loads with slow dynamics, the stability limit will occur at the
same point as the maximum power determined from a power flow analysis (i.e., at the tip of the PV
curve).
The above analysis demonstrates a fundamental problem with the traditional static load model,
described by a second order polynomial (the so-called ZIP model), widely used in large scale
dynamic simulation of power systems. Although the constant power part would usually either be
zero or constitute a small fraction of the total load, on those rare occasions when a significant part of
the load is specified as constant power load, there is the potential for misleading results and/or
computational problems.
A practical illustration of the problem of using a static model for constant power load in a dynamic
simulation is a case study reported in Reference 22. In the second example of that paper, the load,
modeled as a constant power static load, was ramped up and down while operating in the lower
portion of the PV curve. No instability was evident. Although the results are computationally
correct, the apparently stable operation is a consequence of using a static model for the constant
power load in a dynamic simulation, as explained in the analysis presented above.

VOLTAGE STABILITY
10-39
Constant Power Dynamic Load with Fixed Generator Field Voltage
Again, for simplicity, a purely reactive load is assumed. The generator equations are as given in
equations (10.59) - (10.61). The equation for the load, from (10.43), is
LLLL
BVQBT
2
0
−=
&
(10.65)
Linearizing equations (10.59) - (10.61), and (10.65), and eliminating the non-state variables, the
state-space formulation is obtained as
∆
′
∆
=
∆
′
∆
L
q
L
q
B
e
aa
aa
B
e
2221
1211
&
&
where
′′
+
′
−−=
′′
+
−=
′′
+
′
−
′
−=
′′
+
′
+
′
−=
Ld
Ld
L
L
LdL
LL
Ld
dd
do
L
Ld
Ld
do
BX
BX
T
V
a
BXT
BV
a
BX
xx
T
V
a
BX
BX
T
a
1
2
1
)1(
2
11
1
1
2
2221
1211
and
BBB
LL
−
=
′
For stability,
0and0)(
211222112211
>
−
>+− aaaaaa
The first condition is automatically satisfied, provided the second condition is satisfied. After
carrying out the indicated operations and simplifying,
)](1[)](1[
)1(
2
2
21122211
BBXBBX
BXTT
V
aaaa
LdLd
LddoL
L
−
′
++−
′′
+
′
=−
Practical values of B are such that
d
XB
′
<< 1. Therefore, the condition for stability is
1)()(
<
+
+ BBxX
Ld
This is the same condition as would be arrived at by assuming constant voltage behind the
synchronous reactance x
d
(i.e., the field voltage). Therefore in the absence of active excitation
control, generator flux dynamics have no effect on voltage stability limit. The stability limit is
determined by the fixed voltage behind synchronous reactance.
The above analysis demonstrates the importance of operating well within the excitation limit when
the load behavior is constant MVA. In the steady-state analysis of voltage stability, it is common
practice to convert a generator bus from a P, V bus into a P, Q bus when the generator reactive limit
corresponding to a given P is reached. Although this forces the terminal voltage to decrease as the
system loading increases, the situation would be far worse if the computation were carried out with
fixed generator field voltage, which would be the correct procedure. An operating point which has
sufficient stability margin with respect to the controlled generator terminal voltage may be well
within the unstable region with respect to the fixed generator field voltage. When the excitation hits
limit, a stable operating point may suddenly be pushed well into the unstable region.
VOLTAGE STABILITY
10-40
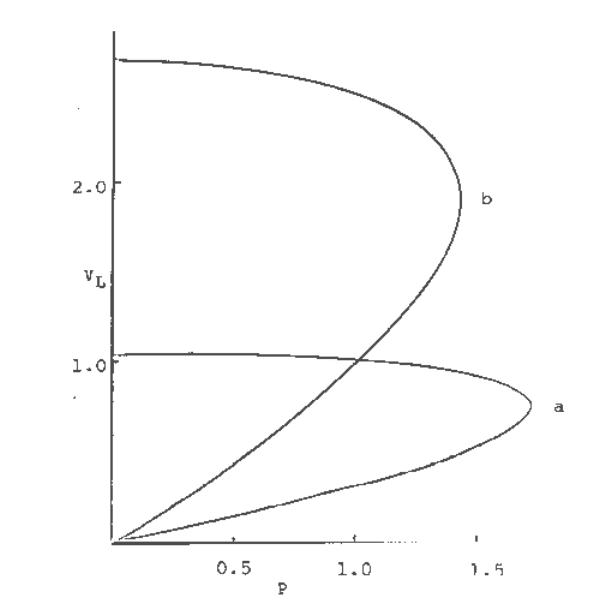
As an illustration, consider the system of Figure 10.16, supplying a unity power factor load P
L
= 1.0,
with parameter values X = 0.3, and x
d
≈ x
q
≈ 1.5. Assume V
S
= 1.0 and V
L
is held constant at unity by
providing sufficient reactive support by shunt capacitors at the load bus. For this operating
condition, the field voltage, E
fd
, is calculated as 1.94, and B = 0.1535. The PV curves corresponding
to operation at constant generator terminal voltage and constant field voltage calculated at the
assumed load (P
L
= 1.0) are shown in Figure 10.24. Curve a applies if the generator terminal voltage
is under active excitation control whose response speed is much faster than the speed of load
recovery, while curve b applies if the excitation is at limit and, therefore, unable to provide voltage
control. It is evident that although the operating point is on the upper part of the PV curve for
constant terminal voltage, and well within the voltage stability limit under active excitation control,
it can be pushed well into the unstable region if the field voltage reaches its upper limit. This is
because, as the above analysis has shown, when the field voltage is held constant, voltage stability is
determined by the fixed field voltage, not the generator terminal voltage.
Fig. 10.24 Power-voltage characteristics
(a)
for constant generator terminal voltage, (b) for constant generator field voltage
Induction Motor Load
Induction motors require special consideration in voltage stability analysis. An induction motor with
constant load torque will generally become unstable well before the voltage stability limit as
determined for loads specified simply by the MVA demand and power factor. Also, the response
speed of a motor load is fast and may be comparable to the speed of response of the voltage control
equipment. However, in situations when the source voltage may be assumed to remain more or less
VOLTAGE STABILITY
10-41
constant, induction motor loads can be correctly accounted for in voltage stability studies by steady-
state analyses.
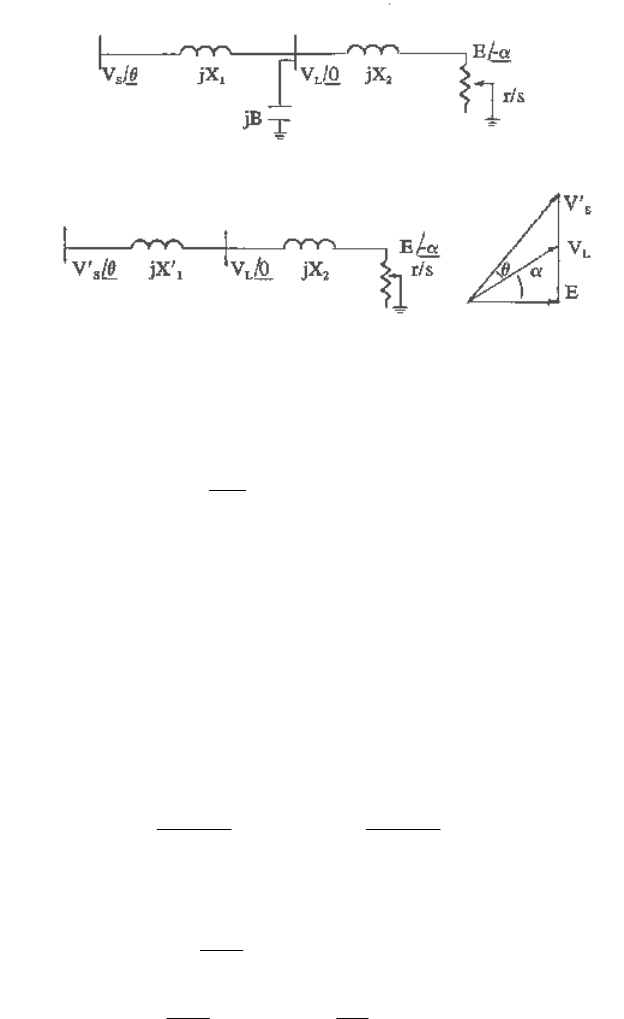
For the purpose of illustration, a simplified motor equivalent circuit will be used and shown in
Figure 10.25a. For simplicity, the mechanical load torque, T
m
, will be assumed to be constant. The
stability condition will first be derived from a dynamic analysis, considering only the basic
dynamics of the motor. The results will then be used to validate the steady-state analysis. [Later it
will be shown that the fundamental conclusion will not change when a more detailed dynamic
model of the motor is employed.]
a
b
Fig. 10.25 Constant voltage source supplying induction motor load
(a) represented by simplified equivalent circuit, (b) Thevenin equivalent of a
The basic equation representing the motor dynamics is
me
TT
H
−=
ω
ω
&
o
2
(10.66)
where H is the inertia constant. Since the slip, s, is given by
oo
/)(
ω
ω
ω
−
=
s , where ω
o
and ω are
the synchronous and motor speeds, respectively, we have,
ω
ω
&&
−
=
s
o
. Also, T
e
= E
2
(s/r). Therefore
equation (10.66) reduces to
GETGT
mL
2
−=
&
(10.67)
where T
L
= 2Hr, and G = s/r. Note that the structure of equation (10.67) is similar to that of (10.43).
The circuit of Figure 10.25a is converted into the Thevenin equivalent shown in Figure 10.25b,
where
1
1
1
1
1
and
1 BX
X
X
BX
V
V
S
S
−
=
′
−
=
′
The power flow equations can be written as
X
E
X
EV
X
EV
GE
S
S
2
2
)cos(0
)sin(
−+
′
=
+
′
=
αθ
αθ
VOLTAGE STABILITY
10-42
where
2
1
1
1
X
BX
X
X +
−
=
Linearizing and eliminating the non-state variables, the following is obtained:
GEGT
L
∆+−=∆ )(2cos
2
αθ
&
(10.68)
Therefore, operation is stable for θ + α < 45
o
, and the stability limit is reached when θ + α = 45
o
Modification of the power flow Jacobian to account for induction motor load
It will now be shown that the same stability condition as implied by (10.68) will also be obtained
from a steady-state analysis by appropriately modifying the conventional power flow Jacobian to
reflect the power-voltage characteristic of the induction motor load. From the equivalent circuit, it is
apparent that the reactive power requirement of an induction motor load, for a given load, increases
as the supply voltage decreases, and vice versa.
Since the load torque is assumed constant, the real power drawn by the motor from the system is
approximately constant in the steady state. From the equivalent circuit, the complex power drawn
by the motor is given by
∗
∗
+
==+
2
/
ˆ
ˆˆˆ
jXsr
V
VIVjQP
L
LLLLL
which yields
2
2
2
2
)/(
)/(
Xsr
srV
P
L
L
+
= (10.69)
2
2
2
2
2
)/( Xsr
XV
Q
L
L
+
= (10.70)
Linearizing (10.69) and (10.70), and eliminating ∆s, the following is obtained:
∆Q
L
= k ∆V
L
(10.71)
where
2
2
2
2
)/(
2
Xsr
XV
k
L
−
−=
Note that, since tan α = (s/r)X
2
(see phasor diagram of Fig. 10.25b), k can also be expressed as
α
α
2cos
sin
2
2
2
X
V
k
L
−=
The power balance equations at the load bus for the power system are
1
1
2
1
1
)1(
cos
sin
X
BXV
X
VV
Q
X
VV
P
L
LS
L
LS
L
−
−=
=
θ
θ
