Mrinal K Pal. Power system stability
Подождите немного. Документ загружается.

1-1
CHAPTER 1
FUNDAMENTALS OF POWER FLOW AND POWER LIMITS
Representation of Transmission Lines
A transmission line has four parameters -- series resistance and inductance, and shunt
conductance and capacitance. These are uniformly distributed along the line. In the derivation
of transmission line equations the following assumptions are usually made:
The line is transposed (or symmetrical), and the three phases are balanced. In practice this is not
entirely true but the unbalance and departure from symmetry are small. The line can therefore be
analyzed on a per-phase basis.
The line parameters, per unit length, are constant, i.e., they are independent of position,
frequency, current, and voltage. This assumption, although approximate, is permissible for most
power system studies.
Equations of a transmission line
The voltage and current on a transmission line depend, in general, upon both time and position.
Consequently, a general mathematical description of the line involves partial differential
equations.
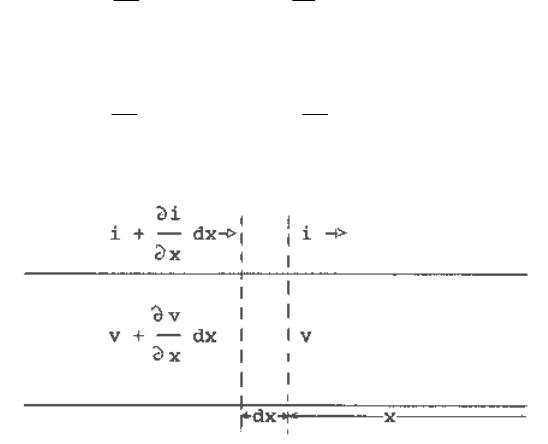
A transmission line section is shown schematically in Figure 1.1. The voltage and current
conditions at a small section of length dx at a distance x from the receiving end of the line is as
shown in the figure. The voltage and current, denoted by v and i respectively, represent
instantaneous quantities. Denoting the series resistance and inductance and the shunt
conductance and capacitance per unit length of the line by r, l, g and c, respectively, the series
voltage for the section dx, is
t
i
ldxirdxdx
x
v
∂
∂
+=
∂
∂
(1.1)
and the shunt current is
t
v
cdxvgdxdx
x
i
∂
∂
+=
∂
∂
(1.2)
Fig. 1.1 Schematic representation of a transmission line.

FUNDAMENTALS OF POWER FLOW AND POWER LIMITS
1-2
Equations (1.1) and (1.2) apply to both steady state and transient conditions. For power flow and
stability analysis purposes we need to consider only the steady state phenomena. The
transmission line transients are fast acting and have negligible impact on system stability except
in special situations. The steady state sinusoidal time variation of voltage and current can be
represented by
tjtj
xItxixVtxv
ωω
εε
)(),(,)(),( ==
Therefore, in the steady state, equations (1.1) and (1.2) reduce to
)()()(
)(
xIzxIljr
dx
xdV
=+=
ω
(1.3)
)()()(
)(
xVyxVcjg
dx
xdI
=+=
ω
(1.4)
where z and y are the series impedance and shunt admittance per unit length of the line,
respectively.
Equations (1.3) and (1.4) can be combined to obtain equations in one unknown, yielding the
following equations. In these equations V and I represent rms values.
Vyz
dx
Vd
=
2
2
(1.5)
Iyz
dx
Id
=
2
2
(1.6)
The solutions of equations (1.5) and (1.6) are
x
cRR
x
cRR
ZIVZIV
V
γγ
εε
−
−
+
+
=
22
(1.7)
x
RcR
x
RcR
IZVIZV
I
γγ
εε
−
−
−
+
=
22
(1.8)
where
y
z
Z
c
=
= the characteristic impedance
yz=
γ
= the propagation constant
Equations (1.7) and (1.8) give the rms values of
V and I, and their phase angles at any distance x
from the receiving end.
Both
Z
c
and
γ
are complex quantities.
γ
can be expressed as
β
α
γ
j+
=
.
α
is called the
attenuation constant and
β
the phase constant.
The two terms in equation (1.7) ((1.8)) are called incident voltage (current) and reflected voltage
(current), respectively. If a line is terminated in its characteristic impedance
Z
c
, V
R
= I
R
Z
c
and
there is no reflected voltage or current, as may be seen from equations (1.7) and (1.8). If a line is
lossless, its series resistance and shunt conductance are zero and the characteristic impedance

FUNDAMENTALS OF POWER FLOW AND POWER LIMITS
1-3
reduces to CL / , a pure resistance. Under these conditions, the characteristic impedance is
often referred to as surge impedance.
The wavelength
λ
is the distance along a line between two points of a wave which differ in phase
of 2
π
radians. If
β
is the phase shift in radians per mile, the wavelength in miles is
LCf
12
≈=
β
π
λ
(1.9)
where
L and C are the series inductance and shunt capacitance per mile, respectively.
At a frequency of 60 Hz, the wavelength is approximately 3,000 miles. The velocity of
propagation of a wave in miles per second is
LC
fv
1
≈=
λ
(1.10)
Equations (1.7) and (1.8) can be rearranged using hyperbolic functions
2
cosh,
2
sinh
θθθθ
εεεε
−−
+
=
−
=
to obtain
xZIxVV
cRR
γ
γ
sinhcosh
+
=
and
x
Z
V
xII
c
R
R
γγ
sinhcosh +=
Letting
x = l, where l is the length of the line,
lZIlVV
cRRS
γ
γ
sinhcosh
+
= (1.11)
l
Z
V
lII
c
R
RS
γγ
sinhcosh += (1.12)
Equations (1.11) and (1.12) can be solved for
V
R
and I
R
to obtain
lZIlVV
cSSR
γ
γ
sinhcosh
−
= (1.13)
l
Z
V
lII
c
S
SR
γγ
sinhcosh += (1.14)
Equations (1.11) through (1.14) are the fundamental equations of a transmission line. For
balanced three-phase lines, the current is the line current, and the voltage is the line-to-neutral
voltage, i.e., the line voltage divided by
3.
Equivalent circuit of a transmission line
A transmission line can be represented accurately by a lumped parameter equivalent circuit
(either a
π or T circuit), insofar as the conditions at the ends of the line are concerned. An
equivalent
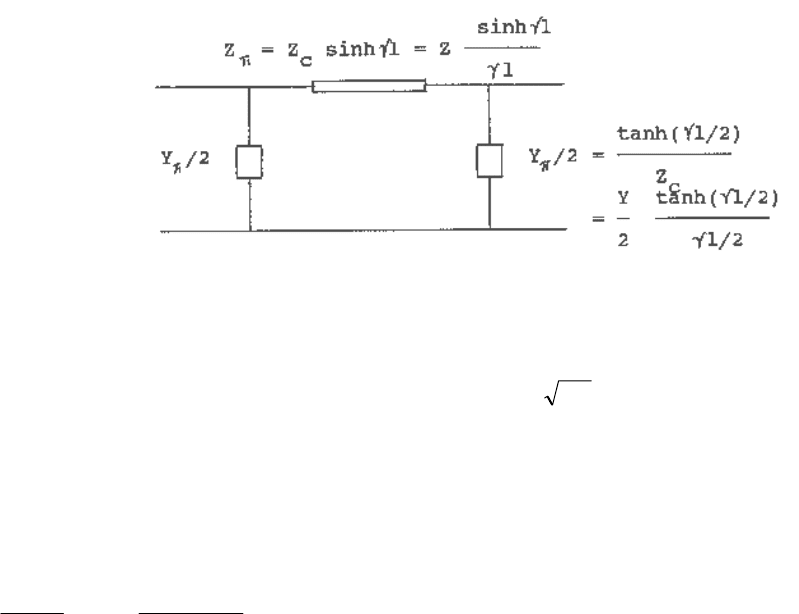
π circuit is shown in Figure 1.2, where the equivalent series impedance and shunt
admittance are also shown.
FUNDAMENTALS OF POWER FLOW AND POWER LIMITS
1-4
Fig. 1.2 Equivalent
π circuit of a transmission line.
Note that
Z (= zl) and Y (= yl) in Figure 1.2 represent the total series impedance and shunt
admittance of the line, respectively. Also note that
γ
l = ZY .
Problems
1. Derive the expressions for Z
π
and Y
π
/2 as shown in Fig.1.2.
2.
Derive the equivalent T circuit.
l
l
γ
γ
sinh
and
2/
)2/tanh(
l
l
γ
γ
are the factors by which the total line series impedance and shunt
admittance are to be multiplied in order to obtain the series impedance and shunt admittances of
the equivalent
π circuit. The correction factors approach unity as
γ
l (or ZY) approaches zero, i.e.,
as the line becomes electrically shorter.
A
π circuit in which the series arm has the impedance Z and each of the shunt arms has the
admittance
Y/2, obtained by setting the correction factors equal to unity, is called a nominal π
circuit. A T circuit with two series arms each of impedance
Z/2 and one shunt arm of admittance
Y is called a nominal T circuit. Nominal π and nominal T are approximations to the equivalent π
and equivalent T, respectively. The approximations are valid for lines less than 100 miles long.
Longer lines may be broken into two or more segments and each segment may be represented by
a nominal
π or T. A nominal π is more convenient for computational purposes and is therefore
more widely used.
Problem
Derive the sending-end voltage (V
S
) and current (I
S
) in terms of the receiving-end voltage (V
R
)
and current (
I
R
), and vice-versa, for both the nominal π and the nominal T circuits.
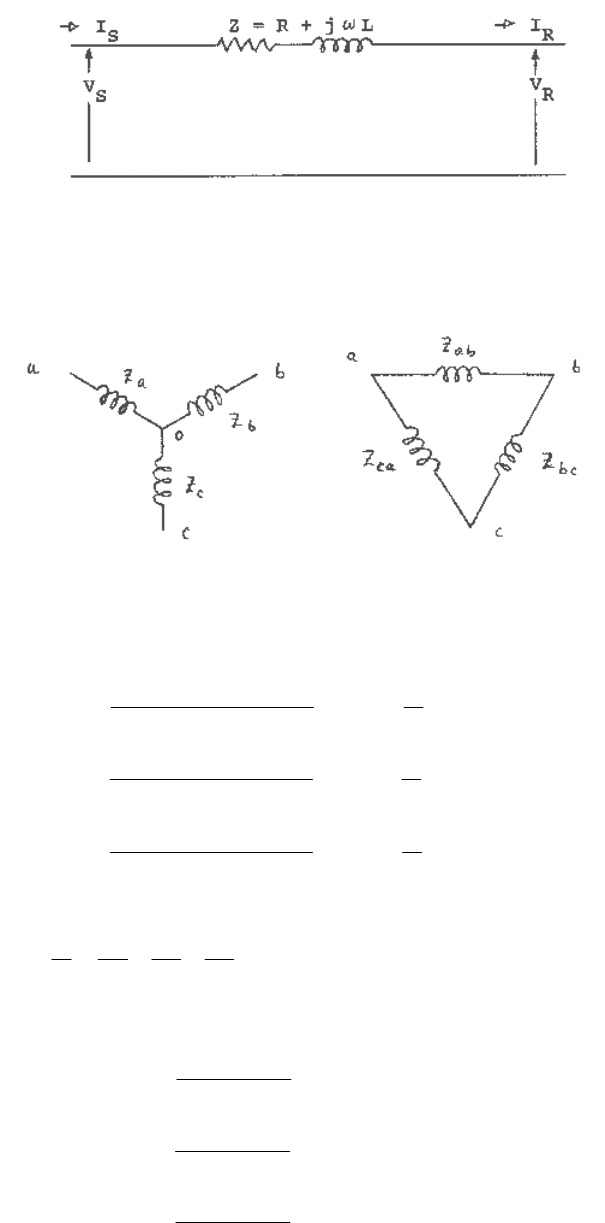
For short transmission lines (less than 50 miles long), the total shunt capacitance is small and can
be neglected. Therefore, a short transmission line, for the purpose of power flow and stability
studies, can be represented by the simple series circuit shown in Figure 1.3.
FUNDAMENTALS OF POWER FLOW AND POWER LIMITS
1-5
Fig. 1.3 Equivalent circuit of a short transmission line.
Y -
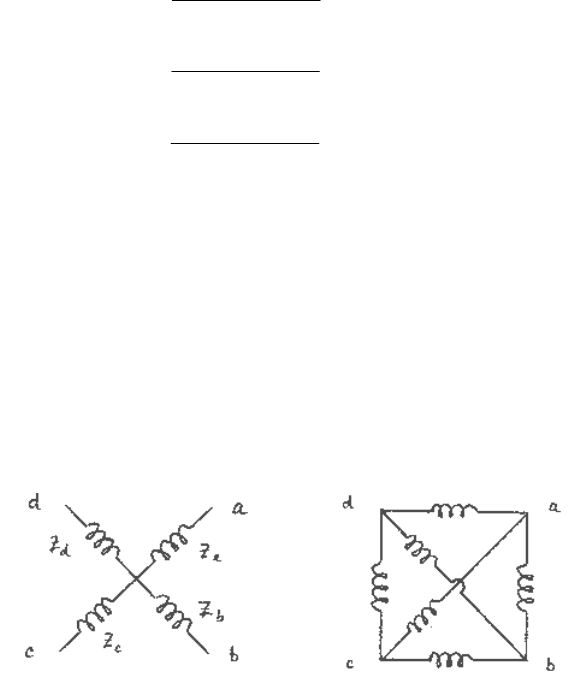
∇ transformations
Fig. 1.4 Y-
∇ equivalent circuits.
The Y circuit in Figure 1.4 can be transformed into the equivalent
∇, and the node o eliminated
by a Y -
∇ transformation. The impedances of the equivalent are
=
++
=
=
++
=
=
+
+
=
Z
ZZ
Z
ZZZZZZ
Z
Z
ZZ
Z
ZZZZZZ
Z
Z
ZZ
Z
ZZZZZZ
Z
ac
b
accbba
ca
cb
a
accbba
bc
ba
c
accbba
ab
1
1
1
(1.15)
where
cba
cba
YYY
ZZZZ
++=++=
1111
In terms of admittances, the above equations can be written as
cba
ac
ca
cba
cb
bc
cba
ba
ab
YYY
YY
Y
YYY
YY
Y
YYY
YY
Y
++
=
++
=
++
=
(1.16)
FUNDAMENTALS OF POWER FLOW AND POWER LIMITS
1-6
Problem
Derive the above expressions for
cabcab
ZZZ ,,
A
∇ circuit can be transformed to an equivalent Y, where the impedances of the equivalent Y are
cabcab
cabc
c
cabcab
bcab
b
cabcab
caab
a
ZZZ
ZZ
Z
ZZZ
ZZ
Z
ZZZ
ZZ
Z
++
=
++
=
++
=
(1.17)
Problem
Derive the above expressions for
cba
ZZZ ,,
If more than three impedances terminate on a node, the node may be eliminated by applying the
general star-mesh conversion equations. However, the conversion is not reversible.
Problem
Convert the star circuit shown in Figure 1.5 into the equivalent mesh circuit and find the
expressions for
Z
ab
, etc.
Fig. 1.5 Star-mesh equivalent circuit.
Per Unit System
In power system computations, great simplifications can be realized by employing a system in
which the electrical quantities are expressed as per units of properly chosen base quantities. The
per unit value of any quantity is defined as the ratio of the actual value to its base value.
Base quantities
In an electrical circuit, voltage, current, volt-ampere and impedance are so related that selection
of base values of any two of them determines the base values for the remaining two. Usually,
base kVA (or MVA) and base voltage in kV are the quantities selected to specify the base.
For single-phase systems (or three-phase systems where the term current refers to line current,
the term voltage refers to voltage to neutral, and the term kVA refers to kVA per phase), the
following formulas relate the various quantities.
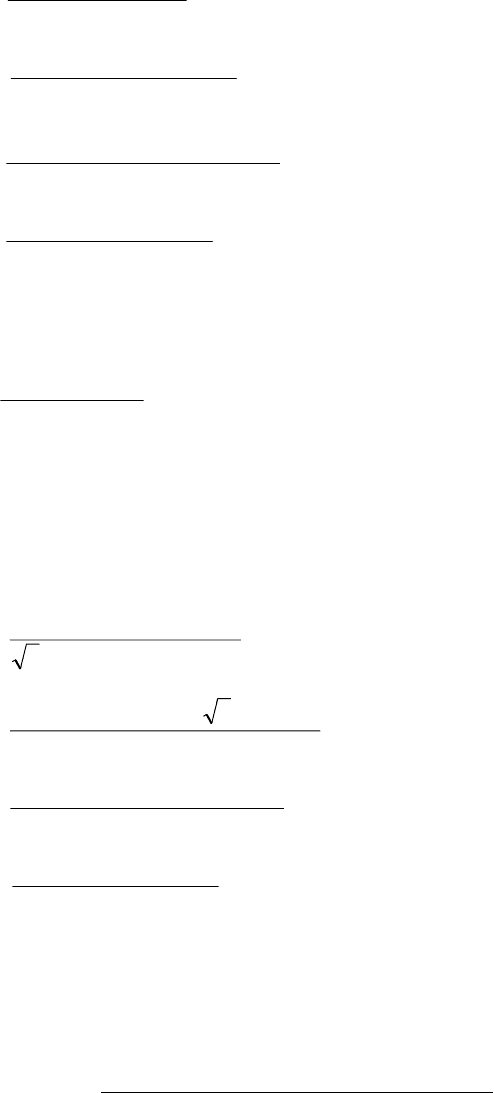
FUNDAMENTALS OF POWER FLOW AND POWER LIMITS
1-7
kVin voltagebase
kVA base
amperesin current Base
= (1.18)
amperesin current base
in volts voltagebase
ohmsin impedance Base
=
kVA
b
ase
1000kV)in voltage(base
2
×
=
MVA
b
ase
kV)in voltage(base
2
=
(1.19)
kVA base kW in power Base =
MVA base MW in power Base =
quantity base
quantity actual
quantity unit Per
= (1.20)
Occasionally a quantity may be given in percent, which is obtained by multiplying the per unit
quantity by 100.
Base impedance and base current can be computed directly from three-phase values of base kV
and base kVA. If we interpret base kVA and base voltage in kV to mean base kVA for the total
of the three phases and base voltage from line to line, then
kVin voltagebase3
kVA base
amperesin current Base
×
=
(1.21)
kVA/3
b
ase
1000)3kV/in voltage(base
ohmsin impedance Base
2
×
=
kVA
b
ase
1000kV)in voltage(base
2
×
=
MVA
b
ase
kV)in voltage(base
2
=
(1.22)
Therefore, the same equation for base impedance is valid for either single-phase or three-phase
circuits. In the three-phase case line-to-line kV must be used in the equation with three-phase
kVA or MVA. Line-to-neutral kV must be used with kVA or MVA per phase.
Change of bases
1000kV)in voltage(base
kVA) (base ohms)in impedance (actual
element circuit a of impedanceunit Per
2
×
×
=
(1.23)
which shows that per unit impedance is directly proportional to the base kVA and inversely
proportional to the square of the base voltage. Therefore, to change from per unit impedance on a
given base to per unit impedance on a new base, the following equation applies:

FUNDAMENTALS OF POWER FLOW AND POWER LIMITS
1-8
=
given
new
2
new
given
givennew
kVA base
kVA base
kV base
kV base
unit per unit Per ZZ
(1.24)
When the resistance and reactance of a device are given by the manufacturer in percent or per
unit, the base is understood to be the rated kVA and kV of the apparatus.
The ohmic values of resistance and leakage reactance of a transformer depend on whether they
are measured on the high- or low-voltage side of the transformer. If they are expressed in per
unit, the base kVA is understood to be the kVA rating of the transformer. The base voltage is
understood to be the voltage rating of the side of the transformer where the impedance is
measured.
HT
H
L
LT
ZZ ×
=
2
kV
kV
(1.25)
where Z
LT
and Z
HT
are the impedances referred to the low-voltage and high-voltage sides of the
transformer, and kV
L
and kV
H
are the rated low-voltage and high-voltage of the transformer,
respectively.
1000)kV(
kVA)kV/kV(
unit per in
2
2
×
××
=
∴
L
HTHL
LT
Z
Z
1000)kV(
kVA
2
×
×
=
H
HT
Z
= Z
HT
in per unit
A great advantage in making per unit computations is realized by the proper selection of
different voltage bases for circuits connected to each other through a transformer. To achieve the
advantage, the voltage bases for the circuits connected through the transformer must have the
same ratio as the turns ratio of the transformer windings.
Per unit and percent admittance
mho
ohm
1
Y
Z
=
, and
Z
Y
1
=
Base admittance
2
kV
MVA
1
b
b
b
b
Z
Y ==
(1.26)
pu
2
pu
1
MVA
kV
ZZ
Z
ZYY
Y
Y
Y
b
b
b
b
b
=====
∴
(1.27)
100,100
pupercentpupercent
×
=
×= YYZZ
percent
4
pu
percent
10
100
1
ZZ
Y =×=
∴
(1.28)
φφ
sin3,cos3 VIQVIP ==
FUNDAMENTALS OF POWER FLOW AND POWER LIMITS
1-9
φ
φ
φ
φ
sin
3
sin3
cos
3
cos3
pupupu
pupupu
IV
IV
VI
Q
IV
IV
VI
P
bb
bb
==
==
∴
(1.29)
Problem
Transmission line charging is usually given in terms of total three-phase Mvar. If a transmission
line has a total line charging of 50 Mvar at 485 kV, what is the per unit admittance on 100 MVA
and 500 kV base?
Power Limits
Power System stability is dependent primarily upon the ability of the electrical system to
interchange energy as required between the connected apparatus. It is therefore necessary to
develop the fundamentals of power flow and power limit of electrical circuits.
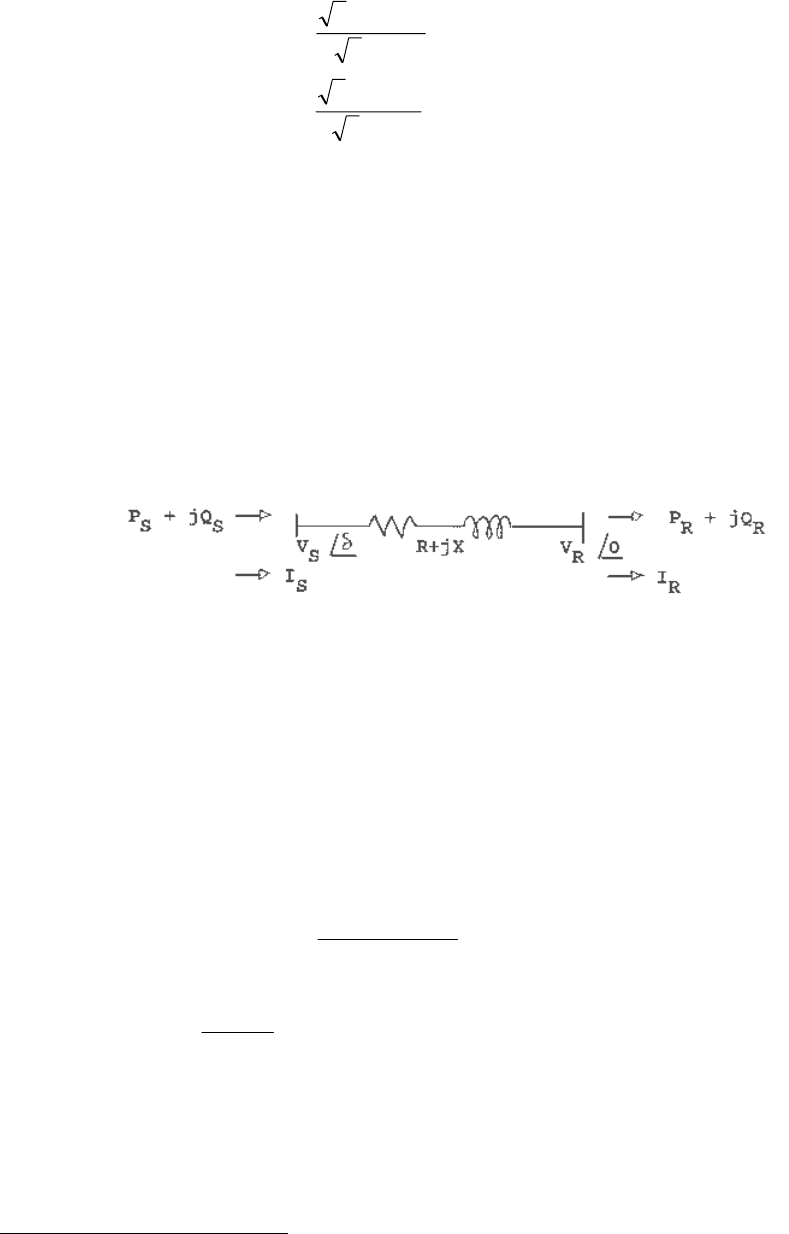
Consider the power flow between two points along a transmission line as shown in Figure 1.6
(the shunt admittance has been neglected).
Fig. 1.6 Schematic of a two terminal transmission line, neglecting shunt admittance.
At the receiving end,
*
ˆˆ
RRRR
IVjQP =+ (1) (1.30)
or
RRRR
IVjQP
ˆˆ
*
=−
(1.31)
Problem
Derive equations (1.30) and (1.31).
From Figure 1.6
()()
jBGVV
jXR
VV
II
RS
RS
SR
+∠−∠=
+
∠−∠
== 0
0
δ
δ
where
jBG
jXR
+=
+
1
, the series admittance.
Substituting the above in equation (1.31),
(
)
(
)
(
)
θδδ
∠−∠=+−∠=− YVVVjBGVVVjQP
RSRRSRRR
22
where
(1) In this and subsequent chapters a “^” is used to distinguish a phasor or complex quantity from a scalar. However,
this is omitted when there is no chance of confusion.

FUNDAMENTALS OF POWER FLOW AND POWER LIMITS
1-10
Z
XR
BGY
11
22
22
=
+
=+=
and
o
90tantan
11
−=−==
−−
αθ
R
X
G
B
where
X
R
1
tan
−
=
α
or
θα
+=
o
90
For normal lines with inductive reactance X,
α
will have a small positive value.
Equating real and imaginary parts,
θθδ
cos)cos(
2
YVYVVP
RSRR
−+=
(1.32)
θθδ
sin)sin(
2
YVYVVQ
RSRR
++−= (1.33)
Alternatively, since
o
90−=
αθ
,
ααδ
sin)sin(
2
YVYVVP
RSRR
−+= (1.34)
and
ααδ
cos)cos(
2
YVYVVQ
RSRR
−+=
(1.35)
In terms of G and B, P
R
and Q
R
can be written as, since YG /sin
=
α
and YB /cos −=
α
,
(
)
δδ
sincos
2
BGVVGVP
SRRR
−+−= (1.36)
and
(
)
δδ
cossin
2
BGVVBVQ
SRRR
−+= (1.37)
When R = 0, G = 0 and B = −1/X, and equations (1.36) and (1.37) reduce to
δ
sin
X
VV
P
SR
R
= (1.38)
and
X
V
X
VV
Q
R
SR
R
2
cos −=
δ
(1.39)
Problem
Derive expressions similar to equations (1.32) through (1.39) for P
S
and Q
S
.
For R = 0, the maximum power that can be transferred, when V
R
, V
S
and X are constant, is, from
equation (1.38),
X
VV
P
SR
R
=
max
(1.40)
