Mrinal K Pal. Power system stability
Подождите немного. Документ загружается.

FUNDAMENTALS OF POWER FLOW AND POWER LIMITS
1-21
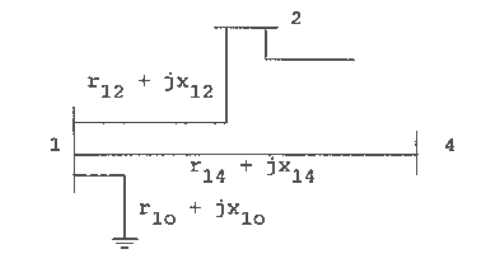
Fig. 1.17 Section of a network for illustrating self and mutual admittances.
14141414
13
12121212
0
jBGyY
Y
jBGyY
+=−=
=
+
=
−=
Problem
Derive equation (1.60)
General equations for real and reactive power
Real and reactive power at node i are given by
∑
=
∗∗
==−
n
k
kikiiiii
VYVIVjQP
1
(1.63)
which, in expanded form, can be written as
[]
niniiiiiiii
VYVYVYVYVjQP +++++=−
∗
LL
2211
)(
2
)(
22
)(
11
2211
ininii
iiii
j
inni
j
iii
j
ii
j
ii
YVVYV
YVVYVV
θδθ
θδθδ
εε
εε
−−
−−−−
+++
++=
L
L
(1.64)
where the
δ
's and
θ
's are the voltage and admittance angles, respectively.
Equating real and imaginary parts, noting that
)(sin)(cos
)(
inininin
j
j
inin
θδθδε
θδ
−−−=
−−
,
)(coscos
)(cos)(cos
2
22221111
inininniiiiii
iiiiiiiii
YVVYV
YVVYVVP
θδθ
θδθδ
−+++
+−+−=
L
L
which can be written as
∑
=
−=
n
k
ikikikkii
YVVP
1
)(cos
θδ
(1.65)
and
)(sinsin
)(sin)(sin
2
22221111
inininniiiiii
iiiiiiiii
YVVYV
YVVYVVQ
θδθ
θδθδ
−++−
+−+−=
L
L
which can be written as
FUNDAMENTALS OF POWER FLOW AND POWER LIMITS
1-22
∑
=
−=
n
k
ikikikkii
YVVQ
1
)(sin
θδ
(1.66)
Alternatively, equation (1.64) can be written as
in
ii
j
niininiiiii
j
iii
j
iiiii
VVjBGVjBG
VVjBGVVjBGjQP
δ
δδ
ε
εε
−
−−
+++++
++++=−
)()(
)()(
2
222111
21
L
L
(1.67)
Equating real and imaginary parts, noting that
inin
j
j
in
δδε
δ
sincos −=
−
,
ininniiiiiii
ininniiiiiiiiiii
BVVBVVBVV
GVVGVGVVGVVP
δδδ
δδδ
sinsinsin
coscoscos
222111
2
222111
++++
+++++=
L
LL
which can be written as
()
∑
=
+=
n
k
ikikikikkii
BGVVP
1
sincos
δδ
(1.68)
and
ininniiiiiiiiii
ininniiiiiiii
BVVBVBVVBVV
GVVGVVGVVQ
δδδ
δδδ
coscoscos
sinsinsin
2
222111
222111
−−−−−−
+++=
LL
L
which can be written as
()
∑
=
−=
n
k
ikikikikkii
BGVVQ
1
cossin
δδ
(1.69)
Elimination of network nodes by matrix method
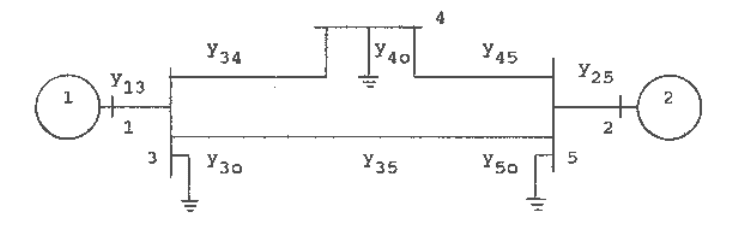
Consider the two-machine three-bus system shown in Figure 1.18. Nodes 3 and 5 correspond to
the terminal buses of machines 1 and 2, nodes 1 and 2 correspond to the machine internal buses.
Note that, including the machine internal buses, the total number of nodes in the system is five.
We wish to eliminate nodes 3, 4 and 5.
Fig. 1.18 Schematic of a three-bus two-machine system.
FUNDAMENTALS OF POWER FLOW AND POWER LIMITS
1-23
The current and voltage relationship can be written in matrix form as
=
5
4
3
2
1
5551
3331
2221
15131211
5
4
3
2
1
V
V
V
V
V
YY
YY
YY
YYYY
I
I
I
I
I
LL
MOM
MLM
ML
L
(1.70)
After partitioning as shown, (1.70) can be written as
=
1
43
21
1
V
V
YY
YY
I
I
(1.71)
Since buses 3, 4 and 5 are passive nodes, the elements of the vector
I
1
are zero. Therefore,
eliminating
V
1
from (1.71) (see Appendix A),
[
]
YVVYYYYI =−=
−
3
1
421
(1.72)
The reduced admittance matrix
Y is given by
3
1
421
YYYYY
−
−= (1.73)
Application of the Steady-State Stability Criterion to an n Machine System
For a single generator connected to an infinite bus a steady-state stability criterion has been
derived earlier. According to this criterion, for steady-state stability, the synchronizing power
coefficient dP/d
δ
is required to be positive at the given operating point. In applying this criterion
to a multi-machine system, the distribution of load among generators in the system due to a small
incremental load change has to be assumed. A conservative steady state limit is obtained if it is
assumed that an increase in shaft load is taken by only one machine, with the added generation
being taken by one other machine, and with all the remaining machines operating at constant
power. If this is done in turn with all the machines in the system, and in all cases the
synchronizing power coefficient turns out to be positive, the system is stable at the assumed
operating condition. Usually the two machines having the largest angular displacement are taken
as the loaded and balancing machines, since these two are the least stable. All the other machines
are treated as constant power machines. Numbering the loaded and balancing machines by 1 and
n, dP/d
δ
1n
and dP/d
δ
n1
should both be positive for stability. These can be calculated as follows:
For an assumed load, under given operating conditions, the internal voltages of all the machines
are calculated. The network is then reduced, retaining only the machine internal buses. The
power output of machine i is given by equation (1.68), repeated here for convenience.
()
niBGVVP
n
k
ikikikikkii
L,2,1sincos
1
=+=
∑
=
δδ
(1.68)
where G
ik
, etc. correspond to the reduced admittance matrix.
FUNDAMENTALS OF POWER FLOW AND POWER LIMITS
1-24
With 0
132
====
−n
dPdPdP L ,
n
nn
nnn
n
nnn
d
d
P
d
d
PP
d
dP
1
,1
,1
1
1
2
2
1
1
1
1
1
δ
δ
δδ
δ
δδδ
−
−
∂
∂
++
∂
∂
+
∂
∂
=
L
LLLL
L
n
nn
nnn
n
nn
d
d
P
d
d
PP
1
,1
,1
2
1
2
2
2
1
2
0
δ
δ
δδ
δ
δδ
−
−
∂
∂
++
∂
∂
+
∂
∂
=
n
nn
nn
n
n
n
n
n
n
n
n
n
d
d
P
d
dPP
d
dP
1
,1
,11
2
211
δ
δ
δδ
δ
δδδ
−
−
∂
∂
++
∂
∂
+
∂
∂
=
L
which can be written in matrix form
∂
∂
∂
∂
∂
∂
=
∂
∂
−
∂
∂
−
∂
∂
−
∂
∂
−
∂
∂
−
∂
∂
−
∂
∂
−
∂
∂
−
∂
∂
−
−
−
−
n
n
n
n
n
n
n
n
n
nn
n
n
n
n
n
nnnn
nnnn
P
P
P
d
dP
d
d
d
dP
PPP
PPP
PPP
1
1
2
1
1
1
1
2
1
1
,132
,1
2
3
2
2
2
,1
1
3
1
2
1
10
00
01
δ
δ
δ
δ
δ
δ
δ
δδδ
δδδ
δδδ
M
M
L
LLL
L
L
(1.74)
From equation (1.74) dP
1
/d
δ
1n
and dP
n
/d
δ
n1
can be computed, since all the elements in the matrix
and the right-hand column vector are known.
∂
P
1
/∂
δ
1n
,
∂
P
1
/∂
δ
2n
, etc. are obtained from equation (1.68), noting that
nn 2112
δ
δ
δ
−= , etc. These
are given by
()
1,2,1cossin
1
−=+−=
∂
∂
∑
≠
=
niBGVV
P
n
ij
j
ijijijijji
in
i
L
δδ
δ
(1.75)
()
ijijijijji
jn
i
BGVV
P
δδ
δ
cossin −=
∂
∂
(1.76)
jinj
ni
≠−=
=
,1,2,1
,2,1
L
L
Problems
1. Verify equations (1.74), (1.75) and (1.76).
2.
Find the expression for dP
1
/d
δ
13
for a three-machine system. Neglect all conductances.
Network Calculation Using Bus Impedance Matrix
Although the use of the bus admittance matrix is generally desirable in the solution of power
system problems, there are situations when the use of the bus impedance matrix can be attractive.
For example, the use of the bus impedance matrix greatly simplifies short circuit computations.
Also, the bus impedance matrix is ideally suited for rapid, approximate analysis of certain system
FUNDAMENTALS OF POWER FLOW AND POWER LIMITS
1-25
contingencies, e.g., loss of a transmission line, loss of a generator, etc. In the past, the bus
impedance matrix also found extensive use in power flow and stability calculations.
The bus impedance matrix can be obtained by a direct inversion of the bus admittance matrix.
For example, from equation (1.62), one can obtain
IZIYV ==
−1
(1.77)
where
Z is the bus impedance matrix.
The direct inversion is not, however, practical when dealing with large systems typically
containing several hundred and frequently well over a thousand buses. A direct inversion can be
avoided by expressing the admittance matrix as a product of two triangular (lower and upper)
matrices and utilizing a process called backward and forward substitution. The bus admittance
matrix is extremely sparse. In a typical power system a particular bus is connected, on an
average, to three other buses and rarely to more than four, so that a typical row or column of the
bus admittance matrix has four non-zero elements. By optimally re-ordering the rows and
columns before factoring, sparsity can be maintained in the resulting triangular matrices. Since
only the non-zero elements need be stored and used in the computation, great savings in
computer time and storage can, therefore, be realized. Various schemes for optimally ordered
triangular factorization are available.
In contrast, the bus impedance matrix is generally full, i.e., there are very few zero elements in
the matrix. If, however, only a small number of elements are required in a particular study, these
can be selectively calculated from the bus admittance matrix using the above technique, thereby
avoiding the necessity to handle the complete matrix.
For small and medium sized systems it can be more convenient to build the bus impedance
matrix directly from network and system parameters. Starting with one bus selected arbitrarily,
the building of the bus impedance matrix proceeds by adding the remaining buses and lines, one
at a time, and applying one of the three basic procedures as new buses and lines are added. Also,
once the bus impedance matrix of the original network has been formed, any modification to it
following a change in the network (line tripping, line closing, etc.) can be easily and efficiently
performed by applying these procedures. These procedures will now be described.
(i)
Adding a new bus to the network
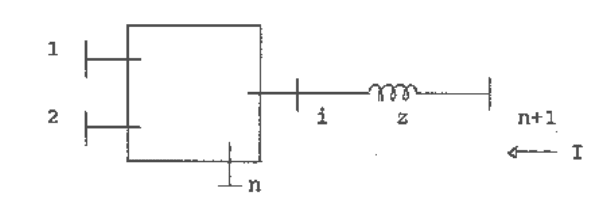
Consider a new bus, numbered n+1, being added to bus i of the network of n buses as shown in
Figure 1.19.
Fig. 1.19 Illustration of the addition of a new bus to an existing network.

FUNDAMENTALS OF POWER FLOW AND POWER LIMITS
1-26
Injecting a unit current at the new bus n+1 is equivalent to injecting a unit current at bus i as far
as the existing network is concerned. Therefore, in accordance with equation (1.78), the changes
in voltages at buses 1, 2, ..., n are
niii
ZZZ ,,,
21
L , respectively.
=
nnnn
n
n
n
I
I
I
ZZ
ZZ
ZZZ
V
V
V
M
L
MOM
L
L
M
2
1
1
221
11211
2
1
(1.78)
The change in voltage at bus n+1 is, from Figure 1.19, Z
ii
+ z, where z is the impedance of the
line between buses i and n+1.
The change in voltage at the new bus n+1 due to a unit injected current at any of the buses 1 to n
will be the same as the change in voltage at bus i due to the same injected current. Therefore,
from the principle of superposition, the modified impedance matrix following the addition of the
new bus will be as shown in equation (1.79).
+
=
++ 1
2
1
21
1
2221
111211
1
2
1
n
n
iiinii
ninnn
in
in
n
n
I
I
I
I
zZZZZ
ZZZ
ZZZ
ZZZZ
V
V
V
V
M
L
L
MMOM
L
L
M
(1.79)
(ii)
Adding a new line between two existing buses
Consider a new line being added between buses i and j as shown in Figure 1.20. When a new line
Fig. 1.20 Illustration of the addition of a new line between two existing buses.
of impedance z is added between buses i and j, a current I will flow on the line as shown in the
figure. This current can be obtained from a knowledge of the Thevenin impedance Z
Th
. Z
Th
can
be obtained by injecting a unit positive current at i and a unit negative current at j and noting the
change in voltage between buses i and j. Following this procedure, Z
Th
is obtained from equation
(1.78) as
(
)
(
)
ijjjiiijjjijiiTh
ZZZZZZZZ 2
−
+
=
+
−
−
−=
(1.80)
for
jiij
ZZ =
Therefore, the current I flowing in the new line between buses i and j is given by

FUNDAMENTALS OF POWER FLOW AND POWER LIMITS
1-27
zZ
VV
I
Th
ji
+
−
=
which yields, using (1.78)
()
zZ
IZZ
I
Th
k
n
k
jkik
+
−
=
∑
=1
(1.81)
Equation (1.81) can be written as
()
()()
0
1
=−++−
∑
=
IzZIZZ
Thk
n
k
jkik
(1.82)
From the viewpoint of the existing network, adding a new line between buses i and j is
equivalent to injecting a current –I at i and +I at j. The change in voltage at bus k, due to the new
line, is then
(
)
IZZV
kjkik
+
−=∆
nk L,2,1
=
(1.83)
Therefore, the new voltage at bus k is given by
kkok
VVV
∆
+
=
which yields, using (1.78)
()
()
1
1
−−+=
∑
=
kjki
n
l
lklk
ZZIZV
nk L,2,1
=
(1.84)
Equations (1.82) and (1.84) can be combined and written in matrix form as
−
+−−−
−
−
−
=
I
I
I
I
zZZZZZZZ
ZZZZ
ZZZZ
ZZZZZ
V
V
V
n
Thjninjiji
njninnn
jin
jin
n
M
L
L
MMOM
L
L
M
2
1
2211
1
22221
1111211
2
1
0
(1.85)
The modified
Z matrix is therefore obtained by eliminating the last row and column of the matrix
of equation (1.85). For example, the lkth element of the modified matrix will be given by
(
)
(
)
zZ
ZZZZ
ZZ
Th
jkikljli
lklk
+
−
−
−=
′
(1.86)
Note: Equations (1.81) and (1.83) can be used to calculate the changes in bus voltages following
a line trip. A line trip is simulated by adding a line of equal impedance and of opposite sign in
parallel with the existing line. Therefore, in order to simulate a line trip, simply put
z = – (impedance of the line to be tripped).
(iii)
Adding a new line between an existing bus and neutral (reference bus).
Following the same argument as presented in (ii), we arrive at an equation similar to equation
(1.85), as shown below:
FUNDAMENTALS OF POWER FLOW AND POWER LIMITS
1-28
−
+
=
I
I
I
I
zZZZZ
ZZZ
ZZZ
ZZZZ
V
V
V
n
Thinii
ninnn
in
in
n
M
L
L
MMOM
L
L
M
2
1
21
1
2221
111211
2
1
0
(1.87)
where Z
Th
= Z
ii
, i is the bus where the new line is connected.
The modified bus impedance matrix is obtained after eliminating the last row and column from
equation (1.87). For example, the lkth element of the modified matrix will be given by
zZ
ZZ
ZZ
Th
ikli
lklk
+
−=
′
(1.88)
The building of the network bus impedance matrix proceeds as follows:
First select a reference bus, usually the neutral (ground). Pick any bus connected to the reference
bus. This bus is numbered 1. The impedance matrix now has one element whose value is the
impedance between the bus numbered 1 and the reference (numbered zero). As new buses and
lines are added, the matrix is modified in accordance with the procedures described in steps (i),
(ii), or (iii). The process is continued until all the buses and lines have been included in the
matrix.
Calculation of Short-Circuit Current
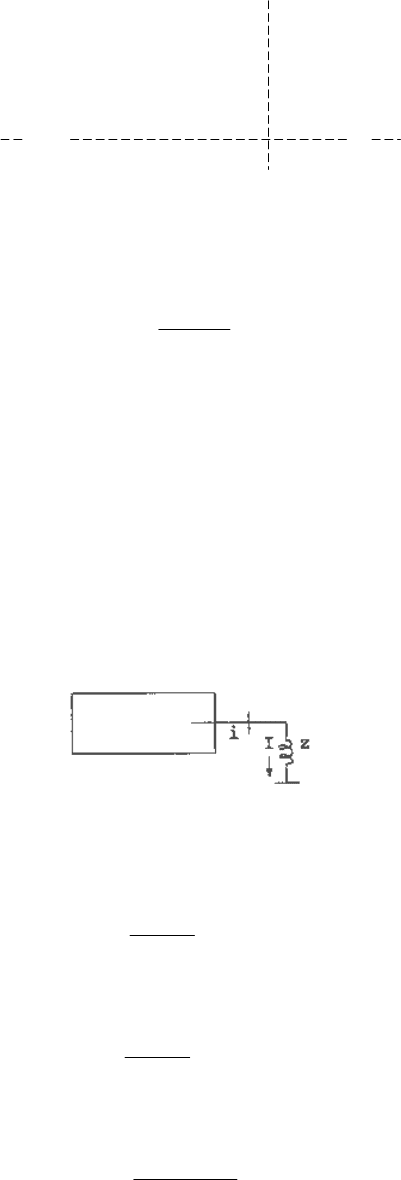
Consider a three-phase fault applied at bus i through an impedance z as shown in Figure 1.21
.
Fig. 1.21 Illustration of the calculation of three-phase short circuit current.
Between bus i and ground, the Thevenin impedance is Z
ii
. Therefore, the short circuit current is
given by
zZ
V
I
ii
i
sh
+
=
(1.89)
The change in voltage at bus k due to this current is given by
zZ
VZ
V
ii
iki
k
+
−=∆
nk L,2,1
=
(1.90)
The change in the current flow on a line connecting buses k and l is given by
kl
lk
kl
z
VV
I
∆
−
∆
=∆ (1.91)
Note: Equation (1.89) can also be derived as follows:

FUNDAMENTALS OF POWER FLOW AND POWER LIMITS
1-29
When bus i is shorted through an impedance z, the voltage of bus i becomes Iz, where I is the
short-circuit current flowing from the bus to ground. Therefore, the change in voltage at bus i is
ii
VzIV
−
=
∆ (1.92)
The change in voltage at bus i is also obtained from equation (1.78) due to an injected current –I
at i, given by
IZV
iii
−
=
∆ (1.93)
Equation (1.89) follows from (1.92) and (1.93).
In many short circuit studies of very large systems, the short circuit information pertaining to a
part of the system is only needed. In such cases it is unnecessary to build and work with the
impedance matrix of the entire system. During the matrix building process, in the addition of a
new bus to an existing one, the only elements that take an active part in the matrix modifications
are the elements of the row and column corresponding to the existing bus. When a new line is
added, the only rows and columns that take an active part in the matrix modification are the rows
and columns corresponding to the buses being connected by the new line. Therefore, when all
lines have been connected to a bus, the elements of the matrix in the row and column
corresponding to that bus will never be required as active participants in the matrix modification.
If the bus is not required in the short circuit analysis, the row and column corresponding to the
bus may be deleted. When all lines have been processed and the rows and columns
corresponding to the buses not required for the short circuit analysis have been deleted following
the above procedure, the remaining matrix will be the impedance matrix corresponding to the
study area, with the effect of the rest of the system properly taken into account.
Representation of Tap-changing Transformers and Phase-shifting Transformers (Power
Angle Regulators) in Power Flow and Stability Studies
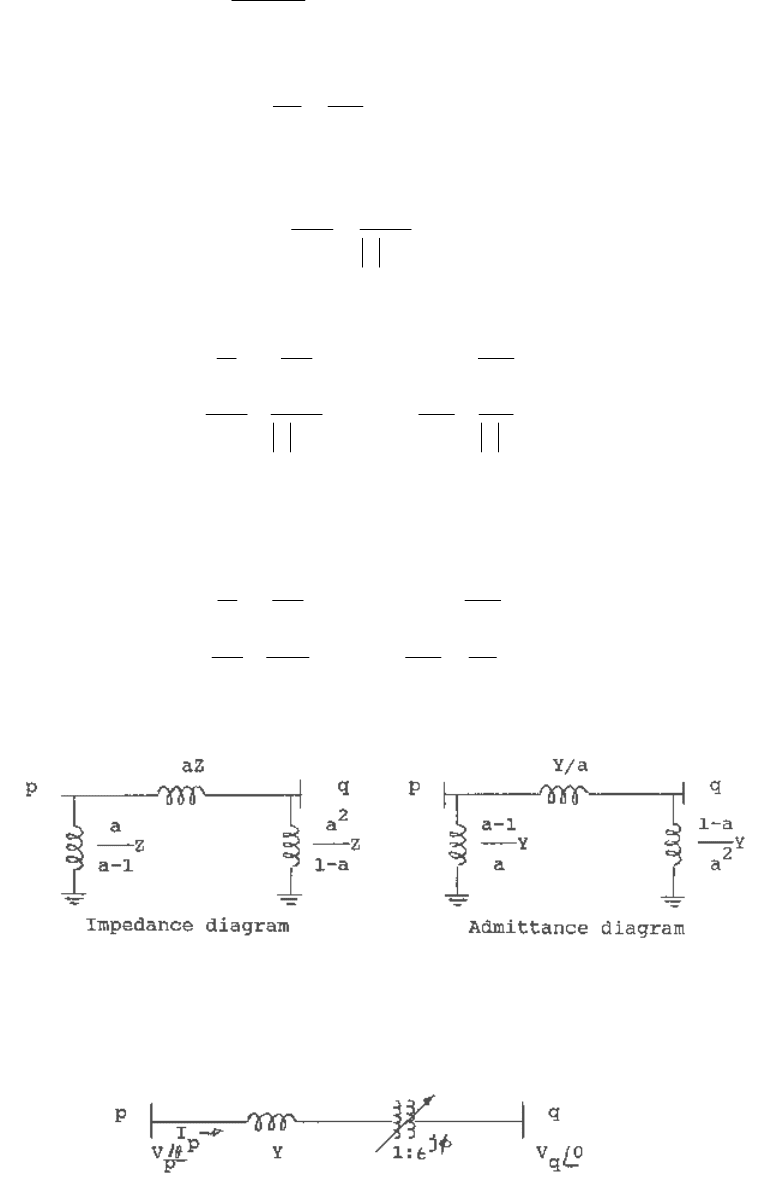
Consider a transformer with off-nominal tap ratio a (per unit) between buses p and q as shown in
Figure 1.22. The impedance Z represents the sum of the transformer leakage impedance and any
other series impedance between buses p and q. a can be real or complex.
Fig. 1.22 Schematic of tap-changing transformer with an off-nominal tap ratio a.
From Figure 1.22
rq
VaV
=
or
aVV
qr
/
=
(1.94)
Equating complex powers on each side of the ideal transformer
∗∗
= IVaIV
rpr
or
∗
= aII
p
/
which yields
∗
−= aII
pq
/ (1.95)
FUNDAMENTALS OF POWER FLOW AND POWER LIMITS
1-30
We have
p
rp
I
Z
VV
=
−
(1.96)
From (1.94) and (1.96), we have
Za
V
Z
V
I
qp
p
−= (1.97)
From (1.95) and (1.97), we have
Za
V
Za
V
I
qp
q
2
+−=
∗
(1.98)
Equations (1.97) and (1.98) can be written in matrix form as
−
−
=
−
−
=
∗∗
q
p
q
p
q
p
V
V
a
Y
a
Y
a
Y
Y
V
V
Za
Za
aZZ
I
I
22
11
11
(1.99)
where
Y = 1/Z
If a is real, as in the case of in-phase tap-changing transformer, (1.99) reduces to
−
−
=
−
−
=
q
p
q
p
q
p
V
V
a
Y
a
Y
a
Y
Y
V
V
Za
aZ
aZZ
I
I
22
11
11
(1.100)
From (1.100), the equivalent circuits of Figure 1.23 follow.
Fig. 1.23 Equivalent circuits of in-phase tap-changing transformer.
Effect of phase-shift on power flow
Consider the example shown in Figure 1.24
Fig. 1.24 Illustration of the effect of phase shift on power flow.
