Mrinal K Pal. Power system stability
Подождите немного. Документ загружается.


STABILITY BASICS
2-19
2
2
o
1
)( xdxxV
x
+=
∫
φ
where
)(x
φ
satisfies the conditions
0for0)(,0)0(
111
≠
>= xxx
φ
φ
The curves
Cxdxx
x
=+
∫
2
2
o
1
)(
φ
naturally must be closed if C is sufficiently small. But if
∫
1
o
)(
x
dxx
φ
tends to a limit a as x
1
→ ∞, then the curves V = C will be closed only for C < a. This
emphasizes the need to verify whether the curves V = C are closed whenever C is not sufficiently
small.
Closure of the curves is assured if, in addition to the above, V approaches infinity as
∞→x
. In
this case V is said to be unbounded.
The simplest and a very useful positive definite function is a quadratic form which may be
written in matrix form as
xPxx
′
=
)(V (2.54)
where P is a real symmetric matrix.
The necessary and sufficient conditions in order that V(x) be positive definite are that the
successive principal minors of the matrix P be positive, i.e.,
L0,0,0
332313
232212
131211
2212
1211
11
>>>
ppp
ppp
ppp
pp
pp
p
(2.55)
This test is, however, unsuitable for large matrices due to the inconvenience of evaluating
determinants of large order. A much better method is to use the fact that P is positive if and only
if it can be expressed as the product of two matrices,
LL
′
, where L is a real lower triangular
nonsingular matrix. The test for nonsingularity can be made very easily as the determinant of a
triangular matrix is simply the product of the diagonal elements.
Stability determined by linear approximation
Considering again the equation )(xfx =
&
, in the majority of problems )(
xf can be expanded into
a convergent power series in a sufficiently small region about the origin. Then (2.53) can be
written as
)(
xFAxx
+
=
&
(2.56)
where
A is a constant nonsingular matrix and the vector function F(x) does not contain terms of
order less than 2.
A sufficient condition for the origin of the nonlinear system (2.56) to be asymptotically stable is
that the eigenvalues of the matrix
A all have negative real parts. If there is an eigenvalue with
positive real part the origin is unstable.
The critical cases are those for which several of the eigenvalues of the matrix
A of the linear
terms are zero or pure imaginary in pairs, while the remaining roots have negative real parts. In
STABILITY BASICS
2-20
all these cases the stability cannot be determined by investigating only the linear terms. In critical
cases the stability is determined by the form of the nonlinearities and then it becomes necessary
to consider equation (2.53) in its original form. However, for our purposes it will not be
necessary to deal with these special cases.
The above theorem of Liapunov is important because it puts on a strong mathematical basis the
engineer’s linearization technique in studying stability under small disturbances.
Extent of asymptotic stability
Asymptotic stability is a local concept, and merely to have established asymptotic stability does
not necessarily mean that the system will operate satisfactorily. Some knowledge of the size of
the region of asymptotic stability is always desirable.
There are several ways of determining the extent of asymptotic stability. One which is useful in
power system problems is as follows. The Liapunov function V is formed such that V
&
is at least
negative semidefinite in the whole state space, and V is positive definite only in a finite region
around the origin. If the largest V = const. closed surface is found, the region within this surface
is the region of stability.
Construction of Liapunov functions
The Liapunov function V(x) may be thought of as a generalized energy. In many problems the
energy function can serve as a Liapunov function. In cases where a system model is described
mathematically, it may not be clear what “energy” means. The conditions which V(
x) must
satisfy in order to be a Liapunov function are therefore based on mathematical rather than
physical consideration.
Although Liapunov’s theorems give sufficient conditions for stability or asymptotic stability they
do not give any indication of how a Liapunov function can be constructed in the general case.
Also, for a particular system there is not a unique Liapunov function. The fact that a particular
Liapunov function ensures stability in a certain region around the equilibrium point, does not
necessarily mean that the motions are unstable outside this region. On the other hand for a stable
or asymptotically stable equilibrium state a Liapunov function with the required properties
always exists.
A lot of work has been done in developing systematic methods of construction of Liapunov
functions. None of the methods devised so far is really effective in generating Liapunov
functions for high order systems with general nonlinearities.
A practical power system is described by nonlinear differential equations of very high order, and
construction of Liapunov functions other than those suitable for studying stability in the small, is
impractical. Claims have been made in the power system literature of successful use of Liapunov
method (also known as energy function method, direct method) in stability analysis of large
power systems. The theory of Liapunov’s direct method has been discussed in some detail here,
so the readers can verify for themselves that all these works, including [10], are mathematically
compromised.
For a linear time-invariant system given by
Axx
=
&
, the scalar function
Pxx
′
can be chosen as a
Liapunov function. If V(x) = Pxx
′
, then ,)()( xV QxxPAPAxx
′
−=+
′′
=
&
where
QPAPA
−
=
+
′
(2.57)
STABILITY BASICS
2-21
If Q is chosen to be positive definite, the necessary and sufficient conditions for the linear
system to be asymptotically stable is that
P is positive definite. Equation (2.57) has a unique
solution for
P if 0≠+
ji
λ
λ
for all i, j, where
i
λ
are the eigenvalues of the matrix A. Using this
approach, the conditions for a positive definite
P matrix, in terms of the signs of the principal
minors, lead to conditions for stability in terms of the a
ij
coefficients. The stability conditions
which are obtained in this manner are of the same type as obtained from Routh’s criterion (see
Appendix B).
Comments on Certain Terms in Common Use
Dynamic stability
Much confusion has existed regarding the use of the expression “dynamic stability.” Originally
the term was intended to address small-disturbance stability in the presence of excitation (and
possibly governor) control. However, over time the term has been used to address other
phenomena (including large-disturbance (transient) stability in some parts of the world). This led
to the discouragement of further use of the term [12]. There is, however, a more fundamental
reason to exclude the term. The question of stability or instability arises only in dynamic
systems, i.e., in systems where changes can and do occur. Therefore, the word “dynamic” in the
above expression is redundant. If used, it can justifiably refer to any and all types of stability or
instability and, in the absence of a universally agreed upon usage, this is precisely what
happened in the past.
Transient/short-term/long-term stability
The same comment as applied to “dynamic stability” also applies to the term “transient
stability.” The question of stability arises during the transients following a disturbance or
disturbances. If there were no transients there would be no instability. Therefore, the word
“transient” is redundant, and if used the term can logically refer to both large- and small-
disturbance stability. However, unlike “dynamic stability,” this term never caused any confusion
as to its intended meaning. This is probably because it was one of the original terms defined in
power system stability and it has been ingrained in the engineers’ mind. The current thinking
seems to favor the expression “large-disturbance stability” so as to be compatible with the
terminology in related fields [11].
When transient stability was originally defined, large-disturbance stability could be assessed by
observing the system response for a brief period immediately following the disturbance. If the
system was stable during the first swing it could be concluded that the system would be stable in
the long run. As power systems expanded and systems were interconnected it became necessary
to simulate several swings before conclusion about stability or instability could be drawn.
Depending on the disturbance and the extent of system disruption and control actions that
followed the disturbance, sometimes it became necessary to extend the simulation to many
seconds or even minutes of real time. To cover these various lengths of simulations, several new
terms were coined. These are: “short-term stability,” “mid-term stability,” and “long-term
stability.” One purpose of this classification was to identify the modeling and solution
requirement for simulations covering the various time periods [12].
We note that to be considered stable a power system must be stable in the long term. A power
system possessing transient or short-term stability as observed from simulation is not of much
use if it cannot be operated stably on a long term basis. Therefore the use of terms like “short-
STABILITY BASICS
2-22
term stability,” etc. seems odd. However, it would seem logical to use the terms “transient
dynamics,” “short-term dynamics,” etc. to refer to the dynamics covering these periods. We can
then say that in a stable system all the dynamics, from transient to long term, are stable. If any of
these is unstable the system is unstable. In most cases experience will dictate that not all these
dynamics need to be analyzed to ensure stability.
Steady-state stability
Originally the expression was used to refer to small-disturbance stability under fixed or manual
control. Later it was retained in order to distinguish from stability under automatic control which
was termed “dynamic stability” [12]. The expression represents a contradiction in terms. If
something is in a steady state, it is stable by definition. However, there is no harm if it is
understood that it refers to small-disturbance stability.
Natural or inherent stability/conditional stability
This classification of stability was mentioned in [12]. Conditional stability was stated as stability
under the action of automatic control as opposed to natural or inherent stability where no control
action is required. The comment was made that since automatic controls are inherent parts of the
system, the concept of natural or inherent stability is redundant. We think that, if desired, the
terms may still be retained, although defined somewhat differently reflecting the current
concepts in emergency controls in power systems. Many power systems are designed to survive
certain disturbances through such control actions as generator tripping, load shedding, etc., much
of which is initiated by the system operator. When stability is maintained through such operator
action(s), the stability may be termed conditional stability (although in a strict sense this is not
stability). If no such control action is required, the system can be considered to possess inherent
stability.
Stability limits
Two types of stability limits are in general use -- small-disturbance (steady-state) limit and large-
disturbance (transient) limit. In a given power system the large-disturbance stability limit cannot
exceed the small-disturbance stability limit, although in some cases the former can closely
approach the latter. This may not always be apparent from simulation results, where large-
disturbance stability simulation results covering a short period of time may suggest a higher limit
than the small-disturbance limit as determined from a linearized analysis. Herein lies the
importance of small-disturbance limit.
A power system cannot be operated above its small-disturbance stability limit although,
depending on the operating criteria, it may be permissible to operate the system above the large-
disturbance limit. This means, whenever there is a disturbance of sufficiently large magnitude,
there will be system disruption and shut down. Depending on the probability of occurrence of
such disturbances this may be an acceptable operating mode. Then the small-disturbance limit
assumes special importance. This also points to the justification of combining the two terms and
simply call it stability limit.
Classification of instability
There has been a trend in classifying angle and voltage instability separately. The problem with
separately classifying angle and voltage instability is that frequently these two go together and
then another term would be needed to identify such cases, although when angle or voltage
instability manifests itself distinctly, one without involving the other, such separate classification
STABILITY BASICS
2-23
can be helpful. A similar comment applies to unidirectional and oscillatory instabilities. When
the instability involves generators, unidirectional and oscillatory instabilities are caused by lack
of sufficient synchronizing torque and damping torque, respectively. However, instability due to
the lack of both synchronizing and damping torque is not uncommon.
Lack of damping or negative damping in the generator rotor oscillations is generally contributed
by the generator excitation control. It has been shown that oscillatory instability can also be
caused by the interaction of excitation control and load dynamics without the participation of the
generator angle [13]. Although it would be tempting to classify such instability under voltage
instability, it is actually a control loop instability [14]. It is shown in Chapter 10 that true voltage
instability is caused by unfavorable load characteristics.
Series capacitors and certain HVDC controls can also contribute to negative damping.
References
1. J.P. La Salle and S. Lefschetz, Stability by Lyapunov's Direct Method with Applications, Academic Press,
N.Y. 1961.
2. W. Hahn, Theory and Application of Liapunov’s Direct Method, Prentice-Hall, Inc., Englewood Cliffs, N.J.
1963.
3. P.M. DeRusso, R.J. Roy and C.M. Close, State Variables for Engineers, Wiley, N.Y. 1965.
4. R.C. Dorf, Modern Control Systems, Addison-Wesley Publishing Co. 1967.
5. K. Ogata, State-Space Analysis of Control Systems, Prentice-Hall, Inc., Englewood Cliffs, N.J. 1967.
6. O.I. Elgerd, Control Systems Theory, McGraw-Hill, N.Y. 1967.
7. W.L. Brogan, Modern Control Theory, 2
nd
Ed. Prentice-Hall, Inc., Englewood Cliffs, N.J 1985
8. A.M. Letov, Stability in Non-Linear Control Systems, Princeton University Press, Princeton, N.J. 1961.
9. J.P. Lasalle, “Some Extensions of Liapunov’s Second Method,” IRE Trans., CT-7, p.520 December 1960.
10. M.K. Pal, “Mathematical Methods in Power System Stability Studies,” Ph.D. Thesis, University of Aston in
Birmingham, 1972.
11. IEEE Task Force on Stability Terms and Definitions, “Approved Stability Definitions,” as of July 1995.
12. IEEE Committee Report, “Proposed Terms and Definitions for Power System Stability,” IEEE Trans., PAS-
101, (7), pp.1894-1898, July 1982.
13. F.P. de Mello, and J.W. Feltes, “Voltage Oscillatory Instability Caused by Induction Motor Loads,” IEEE
Trans., PWRS-11, (3), pp.1279-1285, August 1996.
14. M.K. Pal, discussion of [13].
3-1
CHAPTER 3
SYNCHRONOUS MACHINE STABILITY BASICS
The Swing Equation
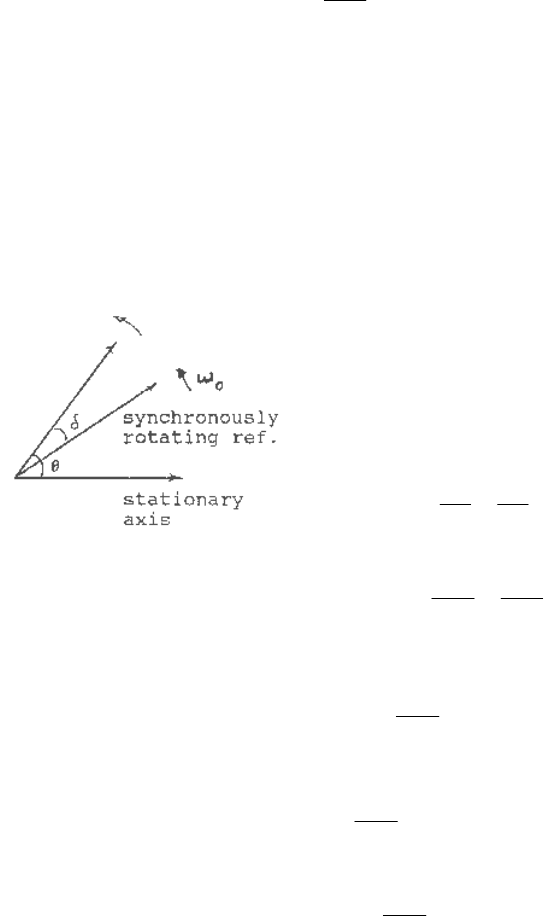
Applying the laws of mechanics to the rotational motion of a synchronous machine
a
T
dt
d
I =
2
2
θ
(3.1)
where I is the moment of inertia of the rotor system,
θ
is the mechanical angle of the rotor in
radians with respect to a fixed reference, and T
a
is the net torque acting on the machine.
The net torque T
a
is the accelerating (or retarding) torque given by
ema
TTT
−
=
(3.2)
where T
m
is the shaft mechanical torque, corrected for rotational losses, and T
e
is the
electromagnetic torque.
In the steady state 0
=
a
T . If we measure the angular position and velocity with respect to
a
synchronously rotating reference axis instead of with respect to
a stationary axis,
t
o
ω
θ
δ
−
=
(3.3)
from which
o
ω
θ
δ
−=
dt
d
dt
d
(3.4)
and
2
2
2
2
dt
d
dt
d
θδ
= (3.5)
Therefore, equation (3.1) becomes
a
T
dt
d
I =
2
2
δ
(3.6)
Equation (3.6) can be written as
o
2
2
o
ω
δ
ω
a
T
dt
d
I =
or
o
2
2
ω
δ
a
T
dt
d
M = (3.7)
where
o
ω
IM = is the angular momentum. At normal speed
ω
o
, the value of M is called the
inertia constant of the machine.
Equation (3.6) can also be written in terms of the stored kinetic energy at rated speed.

SYNCHRONOUS MACHINE STABILITY BASICS
3-2
o
2
2
2
o
o
2
12
ω
δ
ω
ω
a
T
dt
d
I =
or
o
2
2
o
2
ω
δ
ω
a
T
dt
dH
= (3.8)
where
2
o
2
1
ω
IH = (3.9)
From (3.9)
o
2
1
ω
MH =
or
o
2
ω
H
M
= (3.10)
The mechanical angle and speed are related to the electrical quantities by the relations
meme
pp
ωωδδ
2
,
2
==
where p is the number of poles.
Since mechanical input and electrical output are usually expressed in terms of power, it is
convenient to convert torque into power using the relation
T
ω
= P (3.11)
Therefore, equation (3.8) reduces to
o
2
2
o
)
2
(
2
2
ω
ω
δ
ω
a
P
dt
p
d
p
H
=
or
)/1(
/)(
2
o
oo
o
2
2
o
eea
eee
a
e
e
a
e
e
P
P
P
dt
d
H
ωω
ωωωω
ω
δ
ω
∆−=
∆+
==
or
)/1(
2
o
2
2
o
ωω
δ
ω
ea
P
dt
dH
∆−= (3.12)
In equation (3.12) the subscript e has been dropped, since it is understood that
δ
and
ω
refer to
electrical quantities.
Similarly, equation (3.7) reduces to
)/1(
2
o
2
2
ωω
δ
ea
P
dt
d
p
M
∆−= (3.13)

SYNCHRONOUS MACHINE STABILITY BASICS
3-3
Selection of units
ω
om
in radian/sec is calculated from the given rpm of the machine, n.
π2
60
o
n
m
=
ω
(3.14)
In SI units I will be given in kg-m
2
, and H will be in joules or watt-sec. When multiplied by 10
-6
,
this will be expressed in mega joules or megawatt-sec.
Equation (3.12) can be expressed in per unit by dividing both sides by the MVA base.
)/1(
MVAMVA
2
o
2
2
o
ωω
δ
ω
e
b
a
b
P
dt
dH
∆−=
or
)/1(
2
opu
2
2
o
pu
ωω
δ
ω
ea
P
dt
d
H
∆−= (3.15)
where
pu
H
is given in terms of MWs/MVA.
The manufacturers in the United States usually give the value of the moment of inertia in pound-
feet
2
(called WR
2
). The value of H in MWs/MVA can then be computed in one of the following
ways.
(a) Convert the value of the moment of inertia in pound-feet
2
to the SI unit kg-m
2
, using the
relationships:
1 lb = 0.4537 kg, 1 ft = 0.3048 m
Then, if WR
2
= moment of inertia in lb-ft
2
, the inertia in SI unit is
222
m-kg3048.04537.0 ××WR
Therefore
Wsπ4
3600
3048.04537.0
2
1
2
2
22
××××=
n
WRH
MWs10)3048.04537.0(π4
36002
1
622
2
2 −
××××=
n
WR (3.16)
(b) Alternatively
2
22
π4
3600g2
1
××=
nWR
H lb-ft
where g is the acceleration due to gravity = 32.2 ft/sec
2
62
2
2
10
550g
746
π4
36002
1
−
×
×
××=
n
WR MWs (3.17)
It may be observed that the quantities within the parentheses in equations (3.16) and (3.17) are
equal, as they should be.

SYNCHRONOUS MACHINE STABILITY BASICS
3-4
Combining all the constants in equation (3.16) or (3.17), the expression for H can be written as
2210
1031.2 nWRH ×××=
−
MWs (3.18)
Since
ω
o
= 2πf
o
= 120π, equation (3.15) can also be written as
)/1(
π60
o
2
2
ωω
δ
ea
P
dt
dH
∆−= (3.19)
If the deviation from normal speed is negligible
a
P
dt
dH
≈
2
2
π60
δ
(3.20)
Mechanical Torque
The mechanical torques of the prime movers of large generators are functions of speed.
Unregulated machine
For a fixed gate or valve position (i.e., when the machine is not under active governor control)
the torque speed characteristic is nearly linear over a limited range at rated speed.
From the relationship between mechanical torque and power,
ω
/
mm
PT = (3.21)
From (3.21)
ω
ω
ω
∆−∆=∆
2
o
o
1
m
mm
P
PT
(3.22)
For an unregulated machine
∆P
m
= 0. Therefore
ω
ω
ω
ω
∆−=∆−=∆
o
2
o
mm
m
TP
T
or, in per unit,
pupu
ω
∆
−
=
∆
m
T
(3.23)
This relationship is shown in Figure 3.1.
Fig. 3.1 Turbine torque-speed characteristic of an unregulated machine.
