Mrinal K Pal. Power system stability
Подождите немного. Документ загружается.

FUNDAMENTALS OF POWER FLOW AND POWER LIMITS
1-31
We have
pppp
IVjQP
∗
=− (1.101)
Substituting I
p
from (1.99) into (1.101), we have
−=−
∗
qpppp
V
a
Y
VYVjQP
(1.102)
Also
θφ
εε
j
pp
j
VVa == ,
Assuming that the impedance is fully reactive,
2/π
11
j
XjX
Y
−
==
ε
Substituting the expressions for a, V
p,
and Y in (1.102), we have
)2/π(2/π
2
φθ
εε
++−−
−=−
j
qp
j
p
pp
X
VV
X
V
jQP
(1.103)
Equating the real and imaginary parts, we have
)(sin
φθ
+=
X
VV
P
qp
p
(1.104)
)(cos
2
φθ
+−=
X
VV
X
V
Q
qpp
p
(1.105)
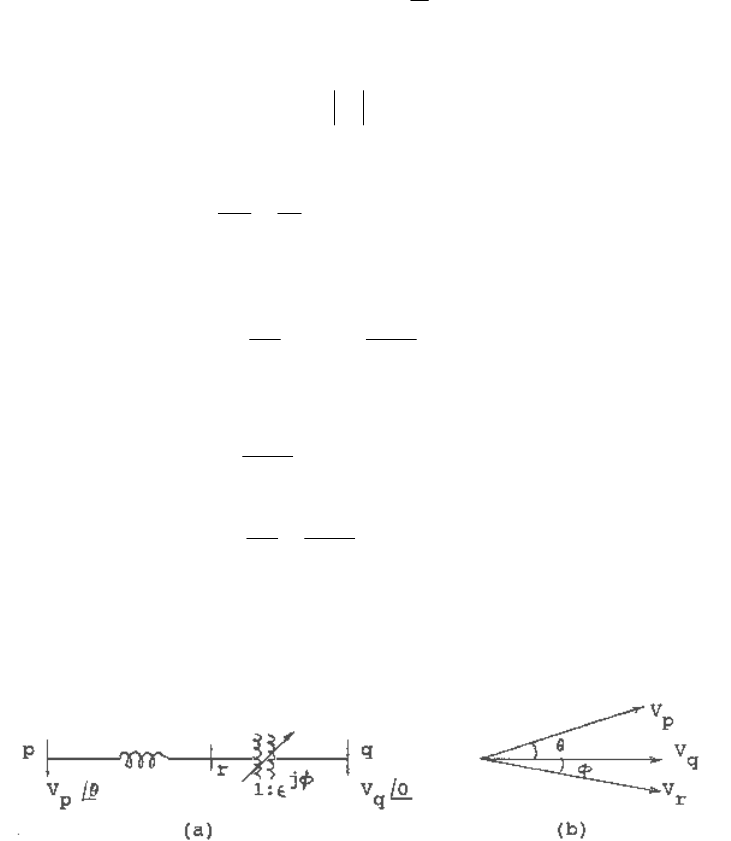
Example 1
A phase shifting transformer with a phase shift
φ
is connected between buses p and q as shown in
Figure 1.25a. The phasor relationship of the voltages is shown in Figure 1.25b.
Fig. 1.25 Phase shifting transformer with phase shift
φ
connected between buses p and q,
and phasor diagram.
Example 2
Consider the arrangement shown in Figure 1.26a, where an ideal phase shifter with a phase shift
φ
is connected between nodes r and q. The phasor relationship of the voltages at various points is
shown in Figure 1.26b.
FUNDAMENTALS OF POWER FLOW AND POWER LIMITS
1-32
Fig. 1.26 An illustration of the effect of phase shifting.
Problem 1
Given the network arrangement shown in Figure 1.27, calculate Q and
φ
as indicated.
Fig. 1.27 Network arrangement for problem 1.
Problem 2
Given a network and initial condition as shown in Figure 1.28, what happens when
φ
is changed
from 0
o
to 20
o
?
Fig. 1.28 Network and system arrangement for problem 2.
References
1. W.D. Stevenson, Elements of Power System Analysis, 2
nd
Ed. McGraw-Hill, N.Y. 1962.
2. E.W. Kimbark, Electrical Transmission of Power and Signals, Wiley, N.Y. 1949.
3. E.W. Kimbark, Power System Stability, Vol.1, Wiley, N.Y. 1948
4. S.B. Crary, Power System Stability, Vol.1, Wiley, N.Y. 1945.
5. O.I. Elgerd, Electric Energy Systems Theory: An Introduction, McGraw-Hill, N.Y. 1971.
6. B. Stott, "Effective Starting Process for Newton-Raphson Load Flows," Proc. IEE, Vol.118, , pp.983-987
August 1971.
7. G.W. Stagg and A.H. El-Abiad, Computer Methods in Power System Analysis, McGraw-Hill, N.Y. 1968.
8. H.E. Brown, Solution of Large Networks by Matrix Methods, 2
nd
Ed. Wiley, N.Y. 1985.

2-1
CHAPTER 2
STABILITY BASICS
A mathematical model describing the operations of a power system contains both differential and
algebraic equations. A power system, like any other dynamic system, is normally subjected to
continuous perturbations. For convenience, we can assume that at a given operating level the
system is at rest, i.e., an equilibrium exists. This implies that we can find a steady-state solution
to the equations describing the operation of the power system. Also, in order to be viable, the
system states at the equilibrium must be within acceptable ranges.
Stability of Dynamic Systems
Consider a dynamic system represented by a vector differential equation of the general form
),,( t
uxfx
=
&
(2.1)
where
x is an n-vector describing the state of the system, and u is the input vector.
If t does not appear explicitly on the right hand side of (2.1) it assumes a simpler form
),(
uxfx
=
&
(2.2)
The set of nonlinear differential equations describing the dynamics of a power system is in
general, at least theoretically, reducible to this form.
A particular point
x* is an equilibrium point if the system’s state at t
o
is x* and x(t) = x* for all t
≥ t
o
in the absence of inputs or disturbances. This means f(x*,0) = 0 for all t ≥ t
o
.
The origin can be transferred to the equilibrium point by a change of variables
x = x* + x
1
For this reason it can be assumed that at the equilibrium point
x
1
= 0, which, after dropping the
subscript, can be written as
x = 0 (2.3)
Stability deals with the following questions: If at time t
o
the state is perturbed from its
equilibrium point, does it return to it, remain close to it, or diverge from it? Similar questions
could be raised if system inputs and disturbances are allowed.
Stability definitions
1. The origin x = 0 is a stable equilibrium point if for a specified positive number
ε
, no matter
how small, it is possible to choose another number
δ
(
ε
) such that
δ
<
o
x implies
ε
<)(tx
for all t ≥ t
o
.
In the contrary case the origin is unstable.
This definition of stability is sometimes called stability in the sense of Liapunov.
2.
The origin is an asymptotically stable equilibrium point if
(a)
it is stable and
(b)
0)(lim =
∞→
t
t
x

STABILITY BASICS
2-2
If
0)(lim =
∞→
t
t
x
occurs for all x
o
the origin is said to be asymptotically stable in the large or
globally asymptotically stable. If, however, this requires
x
o
to be sufficiently small, the origin is
asymptotically stable in the small.
The above definitions of stability of dynamic systems are directly applicable to power systems.
Power system stability definition
A power system at a given operating state is stable if following a given disturbance, or a set of
disturbances, the system state stays within specified bounds and the system reaches a new stable
equilibrium state within a specified period of time.
Comments
Stability as defined above encompasses all types of stability likely to be encountered in power
systems. Examples are: synchronous stability, shaft torsional stability, voltage stability, control
loop stability, etc. It is not necessary to separately define angle (synchronous) or voltage, or any
other stability for that matter. The reason is that frequently they do not manifest themselves
separately, i.e., they may be interrelated. If the stability in question is known to involve only one
aspect exclusively, the same definition can be interpreted to address that aspect only. For
example, if the stability in question involves voltage only, the above definition would be restated
as follows:
A power system at a given operating state and subject to a given disturbance is voltage stable if
voltages near loads approach post-disturbance equilibrium values.
The other reason for not defining the different types of stability separately is that if the system is
to be considered stable it must be stable in every sense. That is, a power system which possesses
synchronous stability but not voltage stability is not acceptable. However, for practical reasons it
is convenient to know the mode of instability when the system becomes unstable so that
corrective measures can be planned and implemented. Two main classes of stability of primary
importance in power system dynamics are:
Small-disturbance stability
If the magnitude of the disturbance is sufficiently small so that the system response in the initial
stage is essentially linear, the stability may be classified as small-disturbance stability (or small-
signal stability, or stability in the small). As will be seen later, small-disturbance stability is
assured if the eigenvalues of the appropriate dynamic model, linearized about the equilibrium
point, have negative real parts. If there is an eigenvalue with positive real part the system is
unstable. Complex eigenvalues occur in conjugate pairs. They signify oscillations. With negative
real parts oscillations damp out.
Note that when a linearized model predicts instability (one or more eigenvalues with positive real
part) it does not necessarily follow that the oscillation amplitude following a disturbance will
increase indefinitely. As the oscillation amplitude increases beyond a certain point, system
nonlinearities and equipment limits may play a dominant role and a limit cycle may be reached.
Then the true system response can only be obtained through a solution of the complete nonlinear
model. Also note that in certain small-disturbance situations equipment limit may be encountered
so that linearization may not be permissible, and the stability should not be classified as such.
STABILITY BASICS
2-3
Although negative real parts of eigenvalues of the linearized system provide sufficient conditions
for small-disturbance stability, in some situations other simpler criteria may be applicable.
Information on small-disturbance stability can also be obtained from a solution of the original
non-linear equations using a small but finite disturbance.
Large-disturbance stability
Large-disturbance stability is assured if the system state at the end of the (final) disturbance lies
within the region of attraction of the stable equilibrium state of the post-disturbance system. An
assessment of large-disturbance stability would generally require numerical simulation. The
importance of the concept of the region of attraction is that, in some situations it can be
determined a priori that the disturbed state is within the region of attraction of the stable post-
disturbance equilibrium, thereby obviating the need for numerical simulation.
We will offer some general comments on the terms and definitions found in the power system
literature later on.
Linear and Non-Linear Systems
A system is defined as linear in terms of the system excitation and response. In general, a
necessary condition for a linear system can be determined in terms of an excitation x(t) and a
response y(t). Suppose that the system at rest is subjected to an excitation
)(
1
tx and the result is a
response
)(
1
ty . Also suppose that when subjected to an excitation )(
2
tx the result is a
corresponding response
)(
2
ty . For a linear system it is necessary that the excitation )()(
21
txtx
+
results in a response
)()(
21
tyty + . This is usually called the principle of superposition.
Furthermore, it is necessary that the magnitude scale factor is preserved in a linear system.
Again, consider a system with an input x which results in an output of y. Then it is necessary that
the response of a linear system to a constant multiple
β
of an input x is equal to the response to
the input multiplied by the same constant so that the output is equal to
β
y. This is called the
property of homogeneity. A system is linear if and only if the properties of superposition and
homogeneity are satisfied.
A system characterized by the relation y = x
2
is not linear since the superposition property is not
satisfied. A system which is represented by the relation y = mx + b is not linear, since it does
not satisfy the homogeneity property. However, both systems can be considered linear about an
operating point x
o
, y
o
for small changes ∆x and ∆y.
Linearization of non-linear systems
A non-linear system can be linearized about an operating point, assuming small changes in
variables. Consider a general non-linear element with an excitation variable x(t) and response
variable y(t), the relationship of the two variables being given as
))(()( txfty
=
(2.4)
The relationship might be shown graphically as in Figure 2.1. The normal operating point is
designated by x
o
, y
o
. Since the curve (function) is continuous over the range of interest, a Taylor
series expansion about the operating point may be utilized. Then we have

STABILITY BASICS
2-4
Fig. 2.1 A graphical representation of a non-linear element.
L+∆
′
′
+∆
′
+==
2
oo
o
)(
!2
)(
!1
)(
)()( x
xf
x
xf
xfxfy
(2.5)
where
o
xxx
−
=∆
For small ∆x higher order terms can be neglected. Therefore
xxfxfy
∆
′
+
= )()(
oo
which yields
xxfy
∆
′
=
∆ )(
o
(2.6)
where
oo
)( yyxfyy
−
=
−
=∆
and
o
)(
o
x
dx
df
xf =
′
is the slope at the operating point.
The same technique can be extended to systems of several variables, represented by a vector
equation of the form
)(xfy
=
(2.7)
where
y is an n-vector of the dependent variables
n
yyy L,,
21
and f(x) is the n-vector function
of the excitation variables
m
xxx L,,
21
.
By employing Taylor series expansion about the operating point
oo2o1
,,
m
xxx L , and neglecting
higher order terms, we obtain the linearized system as
∆
∆
∆
∂
∂
∂
∂
∂
∂
∂
∂
∂
∂
∂
∂
∂
∂
∂
∂
∂
∂
=
∆
∆
∆
m
m
nnn
m
m
n
x
x
x
x
f
x
f
x
f
x
f
x
f
x
f
x
f
x
f
x
f
y
y
y
M
L
MOMM
L
L
M
2
1
21
2
2
2
1
2
1
2
1
1
1
2
1
)()()(
)()()(
)()()(
xxx
xxx
xxx
(2.8)
which can be written as

STABILITY BASICS
2-5
xJy
∆
=
∆
(2.9)
J is called the Jacobian of the system.
Solution of linear differential equations with constant coefficients
Linear time-invariant dynamic systems are represented by linear differential equations with
constant coefficients. Any nth order linear differential equation can be written in the following
form
)(
1
1
1
1
tFxa
dt
dx
a
dt
xd
a
dt
xd
a
o
n
n
n
n
n
n
=++++
−
−
−
L (2.10)
F(t) is called the forcing function. The solution of equation (2.10) consists of two parts
PH
xxx
+
=
(2.11)
The homogeneous or complementary solution,
H
x , is found by replacing F(t) by zero and
solving the resulting homogeneous equation
0
1
1
1
1
=++++
−
−
−
xa
dt
dx
a
dt
xd
a
dt
xd
a
o
n
n
n
n
n
n
L (2.12)
Solution of equation (2.12)
Assume that the solutions are of the form
t
x
λ
ε
= , where
λ
is a constant to be determined.
Substituting the assumed solution into equation (2.12)
(
)
0
1
1
1
=++++
−
−
t
o
n
n
n
n
aaaa
λ
ελλλ
L
For this equation to be satisfied for all values of t,
0
1
1
1
=++++
−
− o
n
n
n
n
aaaa
λλλ
L (2.13)
Equation (2.13) is called the characteristic equation and can be written down directly from
equation (2.12). Equation (2.13) has n roots. Denoting these roots by
n
λ
λ
λ
,,,
21
L the
corresponding solutions to equation (2.12) are
t
n
tt
n
xxx
λ
λλ
εεε
=== ,,,
21
21
L
If these n solutions are linearly independent, the most general solution to the homogeneous
differential equation can be written as
t
n
tt
H
n
KKKx
λ
λλ
εεε
+++= L
21
21
(2.14)
Since the coefficients in equation (2.12) are real, complex roots must occur in complex conjugate
pairs. If one root is
β
α
λ
j+=
1
where
α
and
β
are real, another root must be
β
α
λ
j
−
=
2
.
Then
(
)
() ()
[]
tKKjtKK
KKKK
t
tjtjt
tt
ββε
εεεεε
α
ββα
λλ
sincos
2121
2121
21
−++=
+=+
−
STABILITY BASICS
2-6
For a real system, the a's are real numbers, and
H
x is a real function of time. This means that K
1
and K
2
must be complex conjugates. Therefore, the above can be written as
)cos(
21
21
φβεεε
α
λλ
+=+ tKKK
t
tt
(2.15)
Thus each pair of complex conjugate roots give rise to an oscillatory term in the system
response, the oscillation frequency being determined by the imaginary part of the roots.
The particular integral solution,
P
x , depends upon the input, and is also called the forced
response. For a stable system, the forced solution is identical with the steady-state solution. The
magnitudes of the terms in the forced solution depend upon both the input and the system
parameters.
Evaluation of the arbitrary constants
The arbitrary constants in the complementary solution are evaluated from a knowledge of the
boundary conditions or initial conditions. In most system problems, the values at t = 0
+
of x(t)
and the first n − 1 derivatives are used to evaluate the arbitrary constants in the solution to an nth
order differential equation. The quantities are normally found by examining the stored energy in
the system at t = 0. It is important to emphasize that the arbitrary constants depend upon the
forcing function used and cannot be evaluated until after
P
x has been found.
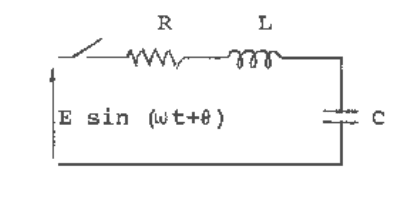
Problem
Find the complete solution for the current in the circuit shown in Figure 2.2 following closing of
the switch at t = 0. Assume that the capacitor is initially uncharged.
Fig. 2.2 An RLC circuit.
Criterion for stability of a linear system
The form of the complementary solution depends only upon the system and not upon the input.
The characteristic equation depends only upon the parameters of the system, and the roots of the
characteristic equation determine the kind of terms appearing in the complementary solution.
The complementary solution represents the natural behavior of the system, when it is left
unexcited. For this reason, the complementary solution is also called the free or unforced
response.
If the free response of a system increases without limit as t approaches infinity, the system is said
to be unstable. This is the case if the characteristic equation has a root with positive real part,
since the complementary solution then contains a term which increases exponentially with t.

STABILITY BASICS
2-7
Roots with negative real parts, on the other hand, lead to terms that become zero as t approaches
infinity. Purely imaginary roots, if they are simple, lead to sinusoidal terms of constant amplitude
in the complementary solution. This case of constant amplitude oscillation in the complementary
solution, which is characteristic, for example, of LC circuits, is usually considered a stable and
not an unstable response. Repeated imaginary roots lead to terms of the form )cos(
φω
+tt
n
,
which is an unstable response. If the roots of the characteristic equation are plotted in a complex
plane, the following statement can be made:
For a stable system, none of the roots can lie in the right half-plane, and any roots on the
imaginary axis must be simple. If all the roots of the characteristic equation lie in the left half-
plane, the system is asymptotically stable.
Concepts of damping ratio and natural frequency
Consider the following second-order system
)(
012
tFxaxaxa
=
+
+
&&&
(2.16)
The characteristic equation of this system is
0
01
2
2
=++ aaa
λλ
(2.17)
Equation (2.17) can be written as
02
2
2
=++
nn
ωλωξλ
(2.18)
in terms of the dimensionless damping ratio
ξ
and the natural frequency
n
ω
of the system. In
this case
2
/ aa
on
=
ω
, and )2(/
21
aaa
o
=
ξ
The roots of the characteristic equation are
1,
2
21
−±−=
ξωωξλλ
nn
(2.19)
When
ξ
> 1, the roots are real, and when
ξ
< 1, the roots are complex conjugates. When
ξ
= 1,
the roots are repeated and real and the condition is called critical damping.
When
ξ
< 1, the response is underdamped and
2
21
1,
ξωωξλλ
−±−=
nn
j
(2.20)
The complementary solution corresponding to this case, from (2.15),
(
)
φωξε
ξω
+−=
−
tKx
n
t
H
n
2
1cos (2.21)
As
ξ
varies with
n
ω
constant, the roots follow a circular locus as shown in figure 2.3. The
transient response is increasingly oscillatory as the roots approach the imaginary axis when
ξ
approaches zero.

STABILITY BASICS
2-8
Fig. 2.3 Locus of roots as
ξ
varies with
n
ω
constant.
Transient response for a unit step input (F(t) = 1) for various values of the damping ratio
ξ
is
shown in Figure 2.4. It can be seen that for
ξ
= 2.0 the system is overdamped.
Fig. 2.4 Transient response of a second order system for a step input.
Although critical damping,
ξ
= 1.0, produces a response with no overshoot, it is evident that a
system with a lower value of
ξ
, for instance, 0.6 <
ξ
< 1.0, approaches the steady state more
quickly (an optimum value for
ξ
is 0.707). Furthermore, the time for the response to come and
remain within the vicinity of the steady state (say, within +
5 percent) is shorter. However,
further reduction in
ξ
to 0.4 and lower produces a definitely oscillatory response that can be quite
objectionable.
