Mrinal K Pal. Power system stability
Подождите немного. Документ загружается.

SELECTED TOPICS FROM CONTROL THEORY
B-5
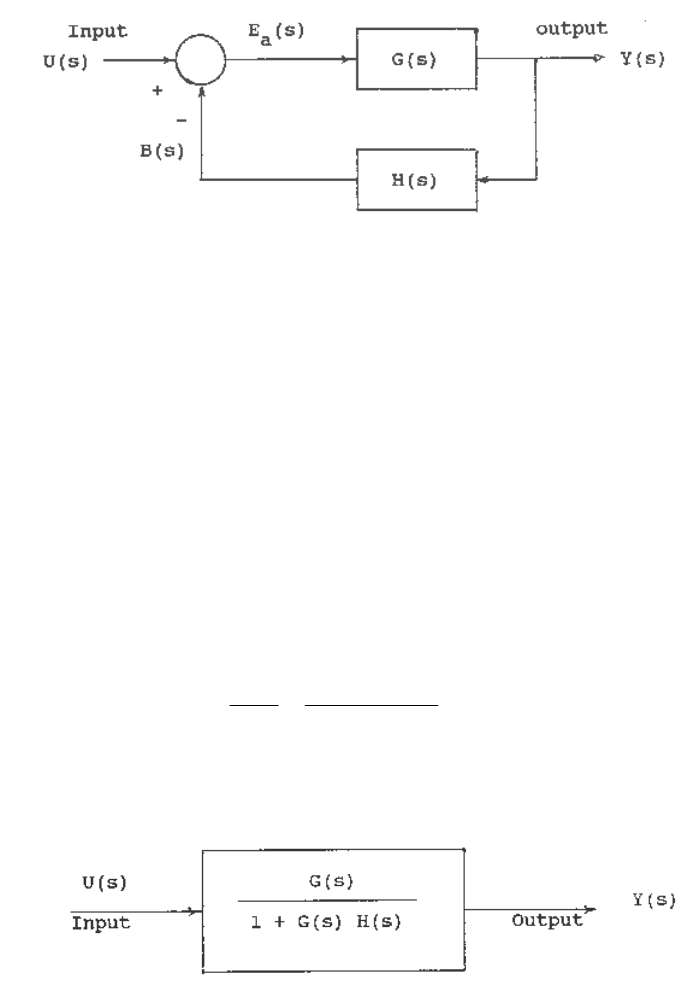
Fig. B.3 A negative feedback control system.
The negative feedback control system is described by the equation for the actuating signal
)()()()()()( sYsHsUsBsUsE
a
−
=
−
= (B.17)
Also, we have
)()()( sEsGsY
a
=
(B.18)
Therefore
[
]
)()()()()( sYsHsUsGsY
−
=
Solving for Y(s) we obtain
[]
)()()()(1)( sUsGsHsGsY
=
+
Therefore, the transfer function relating the output Y(s) to the input U(s) is
)()(1
)(
)(
)(
sHsG
sG
sU
sY
+
= (B.19)
This closed-loop transfer function is particularly important since it represents many of the
existing practical control systems. The reduced block diagram is shown in Figure B.4
Fig. B.4 Reduced block diagram of the system shown in Fig. B.3.
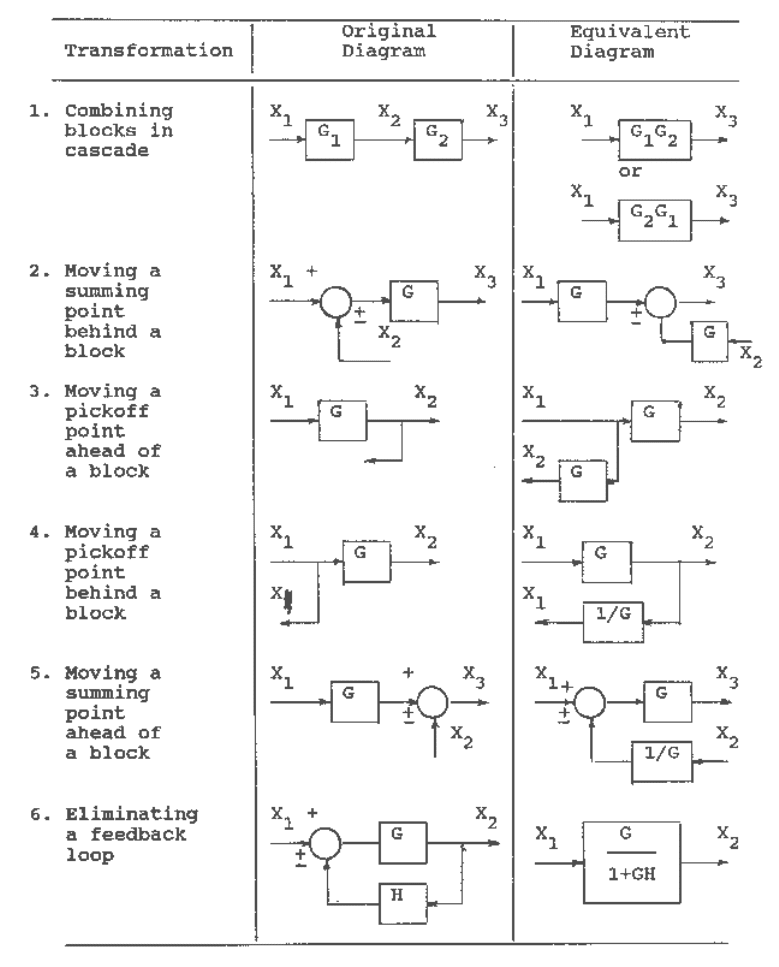
The above is one example of several useful block diagram reductions. These diagram
transformations are given in Table B.2. All the transformations in Table B.2 can be derived by
simple algebraic manipulation of the equations representing the blocks. System analysis by the
method of block diagram reduction has the advantage of affording a better understanding of the
contribution of each component element than is possible by the manipulation of equations.
SELECTED TOPICS FROM CONTROL THEORY
B-6
Table B.2 Block diagram transformation
Open- and closed-loop control systems
A control system can be defined as an interconnection of components forming a system
configuration which will provide a desired system response. Since a desired system response is
known, a signal proportional to the error between the desired and the actual response is
generated. The utilization of this signal to control the process results in a closed-loop sequence of
operations which is called a feedback system.

SELECTED TOPICS FROM CONTROL THEORY
B-7
In order to illustrate the characteristics and advantages of introducing feedback, we shall
consider a simple, single-loop feedback system. An open-loop control system is shown in Figure
B.5a, and a closed-loop, negative feedback control system is shown in Figure B.5b.
Fig. B.5 An open-loop and a closed-loop control system.
The main difference between the open- and closed-loop systems is the generation and utilization
of the error signal. The closed-loop system, when operating correctly, operates so that the error
will be reduced to a minimum value. The signal E
a
(s) is a measure of the error of the system and
is equal to the error E(s) = U(s) - Y(s) when H(s) = 1.
The output of the open-loop system is
)()()( sUsGsY
=
(B.20)
The output of the closed-loop system is
[
]
)()()()()()()( sYsHsUsGsEsGsY
a
−
=
=
from which
)(
)(1
)(
)( sU
sHG
sG
sY
+
= (B.21)
The actuating error signal is
)(
)(1
1
)( sU
sHG
sE
a
+
= (B.22)
Therefore, in order to reduce the error, the magnitude of 1 + GH(s) must be greater than one
over the range of s under consideration.
Sensitivity of control systems to parameter variations
A process G(s), whatever its nature, is subject to change. In the open-loop system this change
will result in a changing and inaccurate output. A closed-loop system senses the change in the
output due to the process changes and attempts to correct the output. A primary advantage of a
closed-loop feedback control system is its ability to reduce the system's sensitivity.
For the closed-loop case, if
1)( >>sHG
, then from equation (B.21),
)(
)(
1
)( sU
sH
sY ≈ (B.23)

SELECTED TOPICS FROM CONTROL THEORY
B-8
That is, the output is only affected by H(s) which may be a constant. If H(s) = 1, the output is
equal to the input. However, it should be noted that 1)( >>sHG may cause the system response
to be highly oscillatory and even unstable. But the fact that as the magnitude of the loop transfer
function GH(s) is increased the effect of G(s) on the output is reduced, is a useful concept.
In order to illustrate the effect of parameter variations, let us look at the incremental equations
derived from (B.20) and (B.21).
From (B.20), the change in the transform of the output is
)()()( sUsGsY
∆
=
∆ (B.24)
From (B.21), the change in the output is
[]
)(
)(1
)(
)(
2
sU
sHG
sG
sY
+
∆
=∆
(B.25)
Comparing equations (B.24) and (B.25), we note that the change in the output of the closed-loop
system is reduced by a factor [1 + GH(s)]
2
which is usually much greater than one.
If system sensitivity is defined as the ratio of the percentage change in the system transfer
function to the percentage change in the process transfer function,
)(/)(
)(/)(
sGsG
sTsT
S
∆
∆
= (B.26)
In the limit (B.26) reduces to
G
T
GG
TT
S
ln
ln
/
/
∂
∂
=
∂
∂
= (B.27)
From (B.20) it can be seen that the sensitivity of the open loop system is equal to one.
The sensitivity of the closed-loop system is obtained from equation (B.21). The system transfer
function is
)(1
)(
)(
sHG
sG
sT
+
=
Therefore, the sensitivity of the feedback system is
)(1
1
sHGT
G
G
T
S
+
=
∂
∂
= (B.28)
Thus the sensitivity of the system may be reduced below that of the open-loop system by
increasing GH(s).
Control of the transient response of control systems
One of the most important characteristics of control systems is their transient response. Since the
purpose of control systems is to provide a desired response, the transient response of control
systems often must be adjusted until it is satisfactory. If an open-loop control system does not
provide a satisfactory response, then the process, G(s), must be replaced with a suitable process.
By contrast, a closed-loop system can often be adjusted to yield the desired response by adjusting
the feedback loop parameters.

SELECTED TOPICS FROM CONTROL THEORY
B-9
As an example, consider the open-loop system with a transfer function as shown in Figure B.6.
Fig. B.6 An open-loop control system.
For a unit step input, the output response is
ss
K
s
sGsY
1
1
1
)()(
+
==
τ
(B.29)
The transient time response is then
(
)
τ
ε
/
1)(
t
Kty
−
−= (B.30)
Now consider the closed-loop system shown in Figure B.7, where the error signal is amplified
before being fed to the process. The amplifier gain K
a
may be adjusted to meet the required
transient response specifications. The feedback gain, K
f
, may also be varied.
Fig. B.7 A closed-loop control system.
The closed-loop transfer function is
KKKs
KK
s
K
KK
s
K
K
sU
sY
fa
a
fa
a
++
=
+
+
+
=
1
1
1
1
)(
)(
τ
τ
τ
(B.31)
Therefore, the transient response for a unit step input is
(
)
τ
ε
/)1(
1
1
)(
tKKK
fa
a
fa
KKK
KK
ty
+−
−
+
= (B.32)
For a large value of the amplifier gain, K
a
, and for K
f
K = 1, the approximate response is
(
)
τ
ε
/
1)(
tK
a
Kty
−
−= (B.33)
Comparing (B.33) with (B.30), it can be seen that using a closed-loop system considerable
improvement in the speed of response can be achieved.

SELECTED TOPICS FROM CONTROL THEORY
B-10
Stability of linear feedback systems
For linear systems the stability requirement may be defined in terms of the location of the poles
of the closed-loop transfer function. The closed-loop system transfer function is written as
)(
)(
)(
sq
sp
sT = (B.34)
where q(s) is the characteristic equation whose roots are the poles of the closed-loop system. A
necessary and sufficient condition that a feedback system be stable is that all the poles of the
system transfer function have negative real parts, i.e., the poles are in the left-hand side of the s-
plane.
In order to ascertain the stability of a feedback control system, one could determine the roots of
the characteristic equation q(s). However, if we are interested only in the knowledge of stability
or instability of a system, several simpler methods are available.
The Routh-Hurwitz stability criterion
The Routh-Hurwitz stability method provides an answer to the question of stability by
considering the characteristic equation of the system. The characteristic equation in Laplace
variable is written as
0)(
01
1
1
=++++=
−
−
asasasasq
n
n
n
n
L (B.35)
In order to ascertain the stability of the system, it is necessary to determine if any of the roots of
q(s) lie in the right-half of the s-plane.
The Routh-Hurwitz criterion is a necessary and sufficient criterion for the stability of linear
systems. The criterion is based on ordering the coefficients of the characteristic equation (B.35)
into an array as follows:
L
MM
L
L
L
L
M
1
531
531
531
42
0
3
2
1
−
−−−
−−−
−−−
−−
−
−
−
n
nnn
nnn
nnn
nnn
n
n
n
n
h
ccc
bbb
aaa
aaa
s
s
s
s
s
where
31
2
1
1
1
−−
−
−
−
−
=
nn
nn
n
n
aa
aa
a
b
51
4
1
3
1
−−
−
−
−
−
=
nn
nn
n
n
aa
aa
a
b
31
31
1
1
1
−−
−−
−
−
−
=
nn
nn
n
n
bb
aa
b
c
and so on.

SELECTED TOPICS FROM CONTROL THEORY
B-11
The Routh-Hurwitz criterion states that the number of roots of q(s) with positive real parts is
equal to the number of changes in sign of the first column of the array. This criterion requires
that there be no changes in sign in the first column for a stable system. This requirement is both
necessary and sufficient.
The root locus method
The relative stability and the transient performance of a closed-loop control system are directly
related to the location of the closed-loop roots of the characteristic equation in the s-plane. Also,
it is frequently necessary to adjust one or more system parameters in order to obtain suitable root
locations. The root locus technique is a graphical method for drawing the locus of roots in the s-
plane as a parameter is varied.
The dynamic performance of a closed-loop control system is described by the closed-loop
transfer function
)(
)(
)(
)(
)(
sq
sp
sU
sY
sT == (B.36)
where p(s) and q(s) are polynomials in s. The roots of the characteristic equation q(s) determine
the modes of response of the system. For a closed-loop system the characteristic equation may be
written as
)(1)( sFsq
+
=
(B.37)
The roots of the characteristic equation is obtained from
0)(1
=
+ sF (B.38)
From (B.38) it follows that the roots of the characteristic equation must satisfy the relation
1)(
−
=
sF (B.39)
In the case of the simple single-loop system shown in Figure B.5b, the characteristic equation is
0)(1
=
+ sHG (B.40)
where
)()( sHGsF
=
The characteristic roots must satisfy equation (B.39). Since s is a complex variable, (B.39) may
be written in polar form as
1)()( −=∠ sFsF (B.41)
and therefore it is necessary that
1)( =sF
and
oo
360180)( ksF ±=∠ (B.42)
L,2,1,0
=
k
As an example consider the system shown in Figure B.8

SELECTED TOPICS FROM CONTROL THEORY
B-12
Fig. B.8 A unity feedback control system.
The characteristic equation representing this system is
0
)(
1)(1 =
+
+=+
ass
K
sG
or alternatively
02)(
2
22
=++=++=
nn
ssKsassq
ωωζ
(B.43)
The locus of the roots as the gain K is varied is found by requiring that
1
)(
)( =
+
=
ass
K
sG
(B.44)
and
L
oo
,540,180)( ±±=∠ sG (B.45)
In this simple example, we know that the roots are
1,
2
21
−±−=
ζωωζ
nn
ss (B.46)
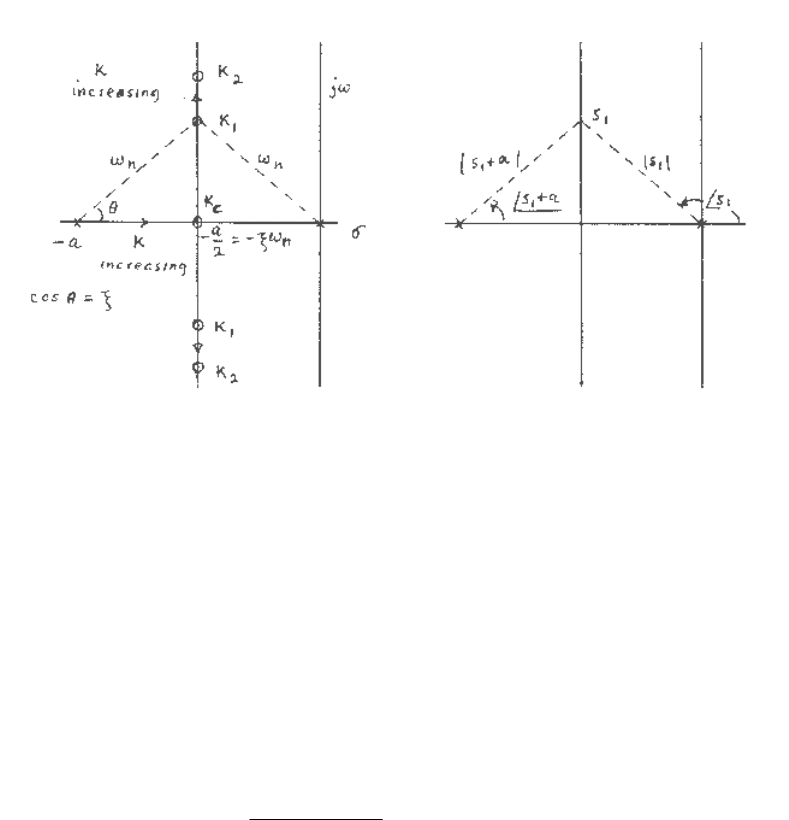
As the gain K is varied from zero to a very large positive value, it can be seen that the roots
follow a locus as shown in Figure B.9, starting at the location of the open-loop poles (0, –a) for
K = 0. For ζ < 1 the locus of the roots is a vertical line in order to satisfy the angle requirement,
equation (B.45). The angle requirement is satisfied at any point on the vertical line which is a
perpendicular bisector of the line 0 to a. Furthermore, the gain K at the particular point s
1
is
found from equation (B.44) as
1
11
=
+ ass
K
or
assK +=
11
(B.47)
where |s
1
| is the magnitude of the vector from the origin to s
1
, and |s
1
+ a| is the magnitude of the
vector from –a to s
1
.
SELECTED TOPICS FROM CONTROL THEORY
B-13
Fig. B.9a Root locus for the system Fig.B.9b Evaluation of the angle
shown in Fig. B.8. and gain at s
1
In order to locate the roots of the characteristic equation in a graphical manner on the s-plane, an
orderly procedure which facilitates the rapid sketching of the locus is required.
The characteristic equation is first written as
0)(1
=
+ sF
The equation is rearranged, if necessary, so that the parameter of interest, K, appears as the
multiplying factor in the form
0)(1
=
+ spK (B.48)
p(s) is factored and the polynomial is written in the form of poles and zeros as follows:
0
)(
)(
1
1
1
=
+
+
+
∏
∏
=
=
N
j
j
M
i
i
ps
zs
K
(B.49)
The poles and zeros are located on the s-plane with appropriate markings. One is usually
interested in determining the locus of roots as K varies from 0 to ∞.
Rewriting equation (B.49), we have
0)()(
11
=+++
∏
∏
==
M
i
i
N
j
j
zsKps (B.50)
Therefore, when K = 0, the roots of the characteristic equation are simply the poles of p(s). Also,
when K → ∞ , the roots of the characteristic equation are simply the zeros of p(s).
Therefore, we note that the locus of the roots of the characteristic equation 1 + K p(s) = 0 begins
at the poles of p(s) and ends at the zeros of p(s) as K increases from 0 to ∞. In most cases several
of the zeros of p(s) lie at infinity in the s-plane.
The root locus on the real axis always lies in a section of the real axis to the left of an odd
number of poles and zeros. This fact is ascertained by examining the angle criterion for the root
locus.

SELECTED TOPICS FROM CONTROL THEORY
B-14
Frequency response methods
A very practical alternative approach to the analysis and design of a system is the frequency
response method. The frequency response of a system is defined as the steady-state response of
the system to a sinusoidal input signal. In a linear system, when the input signal is sinusoidal, the
resulting output signal as well as signals throughout the system, is sinusoidal in the steady state;
it differs from the input waveform only in amplitude and phase angle.
An advantage of the frequency response method is that the transfer function describing the
sinusoidal steady-state behavior of a system can be obtained by replacing s with jω in the system
transfer function T(s). The transfer function representing the sinusoidal steady-state behavior of a
system is then a function of the complex variable jω and is itself a complex function T(jω) which
possesses a magnitude and phase angle. The magnitude and phase angle of T(jω) are readily
represented by graphical plots which provide a significant insight for the analysis and design of
control systems.
Direct correlations between the frequency response and the corresponding transient response
characteristics are somewhat tenuous, and in practice the frequency response characteristic is
adjusted by using various design criteria which will normally result in a satisfactory transient
response.
Frequency response plots
The transfer function of a system G(s) can be described in the frequency domain by the relation
)()()()(
ωωω
ω
jjXjRsGjG
js
+==
=
(B.51)
where
[]
[
]
)(Im)(,)(Re)(
ω
ω
ω
ω
jGjXjGjR
=
=
Alternatively, the transfer function can be represented by a magnitude |G(jω)| and a phase
)(
ω
φ
j as
)()()()(
)(
ωφωεωω
ωφ
jjGjGjG
jj
∠== (B.52)
where
[
]
[
]
222
)()()(
ωωω
jXjRjG +=
and
)(
)(
tan)(
1
ω
ω
ωφ
jR
jX
j
−
=
In order to simplify the determination of the graphical portrayal of the frequency response,
logarithmic plots, often called Bode plots, are employed.
The natural logarithm of equation (B.52) is
)()(ln)(ln
ωφωω
jjjGjG +=
(B.53)
where ln |G(jω)| is the magnitude in nepers. The logarithm of the magnitude is normally
expressed in terms of the logarithm to the base 10, and the following definition is employed.
Logarithmic gain =
)(log20
10
ω
jG
