Mrinal K Pal. Power system stability
Подождите немного. Документ загружается.

SYNCHRONOUS MACHINE STABILITY BASICS
3-5
Regulated machine
In regulated machines the speed control mechanism is responsible for controlling the throttle
valve to the steam turbine or the gate position in hydro turbines, and the mechanical torque is
adjusted accordingly. To be stable under normal operating conditions, the torque speed
characteristic of the turbine speed control system should have a "droop characteristic," i.e., a
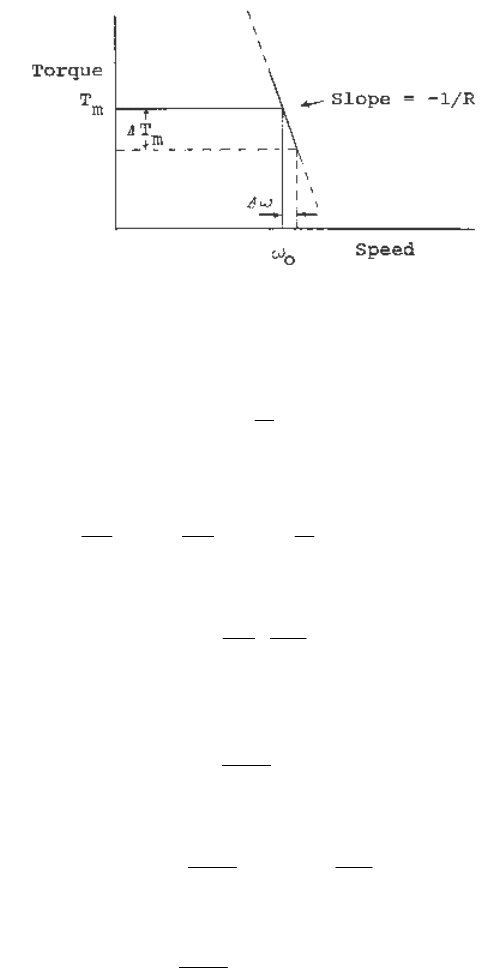
drop in turbine speed should accompany an increase in load. Such a characteristic is shown in
Figure 3.2. A typical "droop" or "speed regulation" characteristic is 5% in the United States (4%
in Europe).
Fig. 3.2 Turbine torque-speed characteristic of a regulated machine.
From Figure 3.2
ω
∆−=∆
R
T
m
1
(3.24)
Therefore, from (3.22) and (3.24),
ωω
ω
ω
∆−=∆−∆
R
P
P
m
m
11
2
o
o
or
o
2
o
ω
ω
ω
∆
−=∆
R
PP
mm
The above equation can be expressed in per unit as
pu
2
o
pu
1
ω
ω
∆
−=∆
m
m
PR
P
or
pu
pu
pu
2
o
pu
1
ωω
ω
∆−=∆−≈∆
RPR
P
m
m
(3.25)
where
)05.0(
2
o
pu
==
ω
m
PR
R
(3.26)
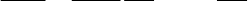
SYNCHRONOUS MACHINE STABILITY BASICS
3-6
If the per unit regulation is to be expressed in the system base, which may be different from the
machine base,
m
s
m
sms
s
P
P
R
P
PPRPR
R
pu
2
o
2
o
pu
===
ωω
(3.27)
The droop characteristic shown in Figure 3.2 is obtained in the speed control system with the
help of feedback. Equation (3.25) describes the steady state regulation characteristics. Transient
characteristics depend on the dynamic response characteristics of the turbine control system
involving various time lags in the feedback elements of the speed control system and in the
steam paths.
Small Disturbance Performance of Unregulated Synchronous Machine System
In this section we investigate the general behavior of an electric power system when subjected to
small disturbances. Such disturbances are always present during normal operation of power
systems. The response of a power system following a disturbance is oscillatory. For stable and
satisfactory operation, oscillations must damp out and the system must return to a steady state in
a reasonably short period of time. Note that if the system survives a large disturbance such as a
system fault followed by opening of one or more transmission lines, the system response, after
the initial impact of the disturbance is over, is essentially determined by the small disturbance
performance of the system.
A good qualitative picture of the basic system dynamic behavior can be obtained by employing
the simplest dynamic model of the power system. In this model the power system is reduced,
retaining only the major synchronous machines in the area under investigation. The number of
synchronous machines retained would depend on the relative impact of these machines on the
particular study. In a simplified analysis intended to reveal the essential dynamic characteristics
of the system, the synchronous machines may be represented by constant voltage magnitude
behind transient reactance (the so-called classical model).
A drawback of the simplified representation is that it excludes machine damping and, therefore,
system simulations using this model fail to reveal the system damping behavior. Damping is
inherently small in electric power systems. The small amount of damping originates mainly in
the synchronous machines due to the electromagnetic interaction, and to some extent in specific
load types. When damping is definitely known to exist, an approximate damping term may be
included in the swing equation. Synchronous machine damping can be significantly affected,
sometimes to the detriment of satisfactory system performance, due to the action of automatic
voltage regulators and governors. Analyses of synchronous machine damping and the effect of
excitation control will be discussed in detail in Chapter 6.
For small disturbance analysis the system equations may be linearized around an operating point
and the stability and dynamic response characteristics of the resulting linear system may be
investigated using the techniques discussed in Chapter 2.
Single machine connected to infinite bus
Consider a synchronous machine connected to an infinite bus through an impedance as depicted
in Figure 3.3. The equation of motion of the synchronous machine is given by

SYNCHRONOUS MACHINE STABILITY BASICS
3-7
dt
d
K
PPP
dt
dH
d
ema
δ
ω
δ
ω
o
2
2
o
2
−−== (3.28)
where P
m
and P
e
are the mechanical input and electrical outputs, respectively, and K
d
is the
damping coefficient
Fig. 3.3 A synchronous machine-infinite bus system.
.
Using the classical representation for the synchronous machine and neglecting all resistances for
simplicity, the electrical output is given by
δ
sin
21
X
EE
P
e
= , where
ed
xxX
+
′
=
Linearizing equation (3.28), noting that
∆P
m
= 0 for an unregulated machine,
dt
d
K
K
dt
dH
d
δ
ω
δ
δ
ω
∆
−∆−=
∆
o
2
2
o
2
(3.29)
where K is the synchronizing power coefficient given by
o
21
cos
δ
δ
X
EE
d
dP
K
e
== (3.30)
Equation (3.29) can be rearranged as
0
22
o
2
2
=∆+
∆
+
∆
δ
ω
δδ
H
K
dt
d
H
K
dt
d
d
(3.31)
The characteristics roots of the system represented by equation (3.31) are
H
K
H
K
H
K
dd
2
16
4
o
2
2
2,1
ω
λ
−±−=
(
)
n
j
ωζζ
2
1−±−= (3.32)
where the natural frequency
ω
n
is
H
K
n
2
o
ω
ω
= (3.33)
and the damping coefficient
ζ is
KH
K
d
o
8
ω
ζ
= (3.34)

SYNCHRONOUS MACHINE STABILITY BASICS
3-8
Since the damping is usually small (ζ << 1), the response is oscillatory with an angular
frequency of oscillation essentially the same as that given by equation (3.33). From the
characteristic roots it is clear that for stability K > 0 and K
d
> 0. If either of these quantities is
negative, the system is unstable.
Modes of Oscillation of an Unregulated Multi-Machine System
Consider a power system with n synchronous machines. Assume that the system has been
reduced retaining only the machine internal buses.
The equation of motion of machine i is
eimiai
ii
PPP
dt
dH
−==
2
2
o
2
δ
ω
(3.35)
In this analysis, the damping coefficients K
di
are assumed to be zero. Since the damping
coefficients are usually small and positive, neglecting them will not alter the modes of oscillation
significantly. However, the computational burden will be reduced considerably.
The expression for P
e
has been derived Chapter 1 and is given by
()
niBGEEP
n
j
ijijijijjiei
,,2,1sincos
1
L=+=
∑
=
δδ
(3.36)
Linearizing equations (3.35) and (3.36),
ei
ii
P
dt
dH
∆−=
∆
2
2
o
2
δ
ω
3.37)
and
()
ij
n
ij
j
ijijijijjiei
GBEEP
δδδ
∆−=∆
∑
≠
=
1
sincos
(3.38)
Since
jiij
δ
δ
δ
∆−∆=∆ , (3.38) can be written as
()
i
n
ij
j
ijijijijjiei
GBEEP
δδδ
∆−=∆
∑
≠
=1
sincos
()
j
n
ij
j
ijijijijji
GBEE
δδδ
∆−−
∑
≠
=1
sincos
∑
=
∆=
n
j
jij
K
1
δ
(3.39)
where
j
i
ij
P
K
δ
∂
∂
=
, and can be called the synchronizing power coefficient between machines i and
j.
Note that in this particular representation

SYNCHRONOUS MACHINE STABILITY BASICS
3-9
∑
=
=
n
j
ij
K
1
0 (3.40)
From (3.37) and (3.39)
niK
dt
dH
n
j
jij
ii
,,2,1
2
1
2
2
o
L=∆−=
∆
∑
=
δ
δ
ω
(3.41)
Equation (3.41) can be written in matrix form as
δPδH ∆=∆
s
dt
d
2
2
(3.42)
where
()
oo2o1
/2,,/2,/2diag
ω
ω
ω
n
HHH L=H
−−−
−−−
−−−
=
nnnn
n
n
s
KKK
KKK
KKK
L
MMM
L
L
21
22221
11211
P
, and
∆
∆
∆
=∆
n
δ
δ
δ
M
2
1
δ
From (3.42)
δKδPHδ ∆=∆=∆
−
s
dt
d
1
2
2
(3.43)
Assume a solution
t
λ
ε
eδ =∆
Then
tt
λλ
εελ
eKe =
2
from which
[
]
0eKI =−
t
λ
ελ
2
(3.44)
Equation (3.44) has a nontrivial solution only if
0
2
=− KI
λ
(3.45)
Therefore, for stability all the roots,
λ
2
, of equation (3.45), i.e., the characteristic values (or the
eigenvalues) of the matrix
K, must be real and negative. If any of the roots is real and positive,
the system is unstable.
Actually, since the matrix
K is singular (the columns add up to zero, since
∑
= 0
ij
K
) one of the
eigenvalues is always zero, since there are (n-1) independent
∆
δ
's. This can be avoided by
taking one machine as a reference. If machine n is taken as a reference, the modified
K matrix
would be obtained by deleting the nth column and subtracting the nth row from every other row.
The modified
K matrix would then become
SYNCHRONOUS MACHINE STABILITY BASICS
3-10
−−
−−
−−
−−
−−
−−
−−
−−
−−
=
−
−
−−
−
−
−
−
−−
−−
n
nn
n
nn
n
n
n
n
n
n
n
n
n
nnn
n
n
n
n
n
nnn
n
n
n
n
H
K
H
K
H
K
H
K
H
K
H
K
H
K
H
K
H
K
H
K
H
K
H
K
H
K
H
K
H
K
H
K
H
K
H
K
222222
222222
222222
1,o
1
1,1o
2o
1
2,1o
1o
1
1,1o
1,o
2
1,2o
2o
2
22o1o
2
21o
1,o
1
1,1o
2o
1
12o1o
1
11o
1
ωω
ω
ω
ω
ω
ωω
ωωωω
ωω
ωωωω
L
MMM
L
L
K
For stability, the (n−1) eigenvalues of K
1
must be real and negative. This means that the system
represented by equation (3.43) has 2(n−1) imaginary roots or (n−1) conjugate pairs. Therefore,
the system has (n−1) natural frequencies of oscillations.
Problem
Derive the condition for stability of the two machine system shown in Figure 3.4.
Fig. 3.4 A two-machine system.
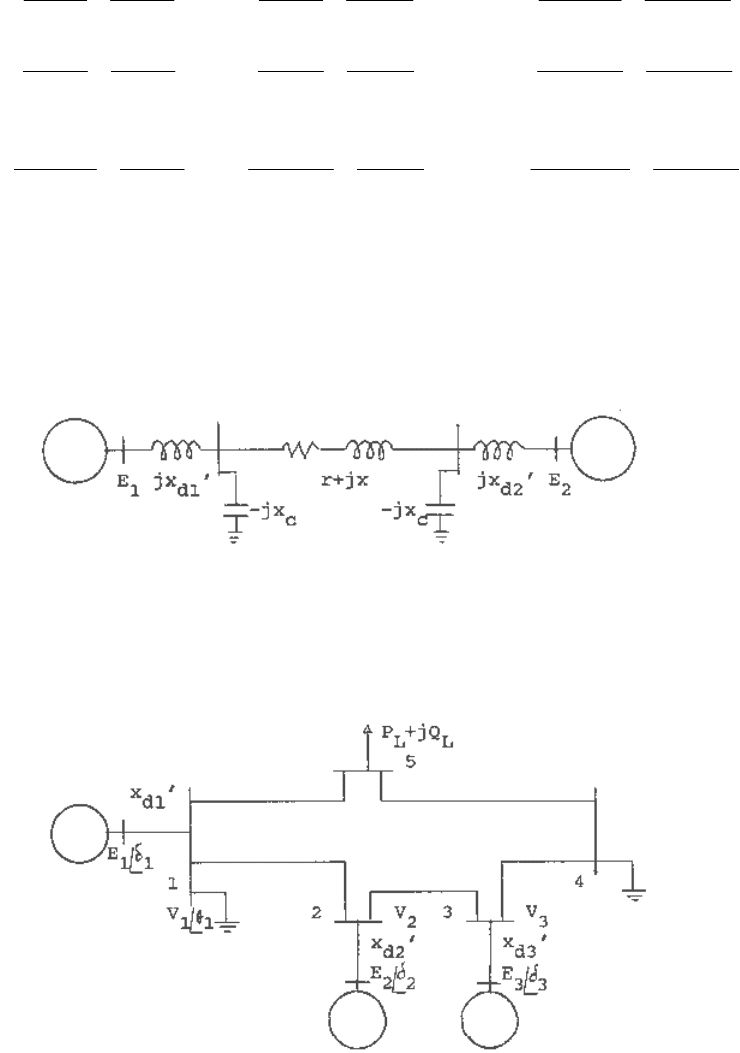
The following steps are involved in computing the modes of oscillation of a multi-machine
system. The system shown in Figure 3.5 is used for the purpose of illustration.
Fig. 3.5 A three-machine five-bus power system.
1. At a given load level, the bus voltages (magnitudes and angles) are first obtained from a
power flow solution. Since P, Q, V and
θ
are known at the machine terminals, the internal
voltages and angles of the machines can be computed as shown in Chapter 1.
SYNCHRONOUS MACHINE STABILITY BASICS
3-11
2. Since non-synchronous loads do not significantly influence the modes of oscillation, very little
error will be incurred by representing loads as constant impedances (or admittances). Therefore,
all loads are converted into equivalent admittances. This can be done as follows:
IVjQP
LL
*
=− (3.46)
where V is the bus voltage and I is the current into the load given by
L
YVI
=
(3.47)
where Y
L
is the equivalent load admittance.
From (3.46) and (3.47)
2*
V
jQP
VV
jQP
V
I
Y
L
−
=
−
==
from which
22
V
Q
j
V
P
Y
L
−= (3.48)
3. The network is then reduced, retaining only the machine internal buses. This can be done in
several ways. A general method suitable for stability computations discussed in later chapters
will be illustrated here.
The network equation in terms of the bus admittance matrix is formed by treating the machine
internal buses as additional system buses as shown in equation (3.49).
′
+
′
−
′
+
′
−
′
+
′
−
′
−
′
′
−
′
′
−
′
=
5
4
3
2
1
3
2
1
5551
44
3
33
3
2
2221
2
1512
1
11
1
33
22
11
3
2
1
11
11
11
11
11
11
V
V
V
V
V
E
E
E
YY
Y
xj
Y
xj
xj
YY
xj
YY
xj
Y
xj
xjxj
xjxj
xjxj
I
I
I
dd
dd
dd
dd
dd
dd
LL
M
M
ML
L
(3.49)
Y
11
, Y
12
, etc. are the elements of the network admittance matrix. Since the loads have been
converted into equivalent admittances and the machine terminal buses are now passive buses due
to the inclusion of the machine internal buses into the system network, the injected currents at all
the buses except at those corresponding to the machine internal buses are zero.
SYNCHRONOUS MACHINE STABILITY BASICS
3-12
For a system of m generators and n buses (3.49) can be written as
+−
−
=
−−
−−
V
E
YY
YZYZ
ZZI
43
2
1
1
1
11
MM
MM
(3.50)
where
Z
M
= m × m diagonal matrix composed of the machine internal impedances
I = vector of generator currents
E, V = vectors of machine internal voltages and network bus voltages, respectively
Y
1
, Y
2
, etc. = submatrices obtained by partitioning the network admittance matrix Y
N
=
43
21
YY
YY
Y
N
From (3.50) we can compute the network bus voltages, which may be needed in some stability
studies, as
E
0
Z
YV
=
−
−
1
1
M
MN
(3.51)
where
+
=
−
43
2
1
1
YY
YZY
Y
M
MN
From (3.50) and (3.51)
[]
E
0
Z
Y0ZEZI
−+=
−
−−−
1
111
M
MNMM
(3.52)
After carrying out the operations indicated in (3.52), we obtain
[
]
EZZYZEZI
1
1
111 −
−
−−−
+−=
MMRNMM
(3.53)
where
Y
RN
is the reduced network admittance matrix (see Chapter 1).
3
1
421
YYYYY
−
−=
RN
Equation (3.53) can be written as
I = YE (3.54)
where
[
]
1
1
111 −
−
−−−
+−=
MMRNMM
ZZYZZY
Y
MN
is, in general, very sparse and in a large scale stability computation it may be more
convenient and desirable to obtain
I directly from (3.52) by exploiting this sparsity.
From (3.52) (as well as (3.53)) it is evident that the same results as obtained from the above
procedure can also be obtained as follows:

SYNCHRONOUS MACHINE STABILITY BASICS
3-13
Convert each of the machine internal voltages in series with the transient reactance into a current
source, I =
d
xjE
′
/ , in parallel with
d
xj
′
; include the shunts thus obtained into the network
admittance matrix and obtain the machine terminal voltages from the relation
11
IYV
−
=
MN
, where
1
I is the vector whose elements are
dii
xjE
′
/ ; then obtain the machine currents from the relation
mixjVEI
diiii
,,2,1/)( L=
′
−= .
Alternatively, for each generator
d
xj
VE
I
′
−
=
Therefore, for the entire network we can write
V
00
0Z
E
0
Z
0
I
−
=
−− 11
MM
(3.55)
The network equation
VY
0
I
N
=
(3.56)
From (3.55) and (3.56)
VYE
0
Z
MN
M
=
−1
from which (3.51) follows.
Substituting (3.51) in (3.55) and simplifying, we obtain (3.52), from which (3.54) follows.
4. The elements K
ij
are computed from equation (3.39) and the matrix K is formed.
5. The eigenvalues of the matrix
K are then computed using an eigenvalue computing
subroutine. For stability, all the eigenvalues must be real and negative.
6. The square roots of the negative of these eigenvalues are the natural frequencies of
oscillations.
An alternative solution for the modes of oscillation of an unregulated multi-machine system
Equation (3.43) can be written, using variables L,,
21
xx to denote ,,,
21
L
δ
δ
∆
∆
as
2
2
dt
d
x = Kx (3.57)
Using a transformation
x = Mz (3.58)
where
M is the modal matrix (see Chapter 2),
we have
2
2
dt
d
z = M
-1
KMz = Dz (3.59)
where
(
)
L,,diag
21
λ
λ
=D
SYNCHRONOUS MACHINE STABILITY BASICS
3-14
,,
21
λ
λ
etc. are the eigenvalues of the matrix K.
Therefore
,,
22
2
2
2
11
2
1
2
z
dt
zd
z
dt
zd
λλ
== etc. (3.60)
For stability
λ
1
,
λ
2
, etc. must be real and negative.
The solutions to the above second order equations are of the form
,)cos(,)cos(
22221111
φ
ω
φ
ω
−
=
−= taztaz etc.
where
,,
2211
λωλω
−=−= etc.
The constants a′s and
φ
′s depend on the initial condition. For example, if the initial perturbation
is such that 0
o2o1
=== L
&&
xx , then
0xMz ==
−
o
1
o
dt
d
dt
d
which yields
0
21
=
=
= L
φ
φ
Therefore
z = R(t) a
where
()
L,cos,cosdiag)(
21
ttt
ω
ω
=R
[]
′
= L
21
aaa
From the above
a = z
o
= M
-1
x
o
which yields
x = M R(t) M
-1
x
o
(3.61)
The general solution can be written as
−
−
−
=
MMM
L
L
L
M
)cos(
)cos(
)cos(
333
222
111
333231
232221
131211
3
2
1
φω
φω
φω
ta
ta
ta
eee
eee
eee
x
x
x
(3.62)
The relationship between the various modes and mode shapes and the system response can be
seen in equation (3.62). For example, if e
11
= 0, the first mode is absent in the variable x
1
. Also, if
e
21
and e
31
are of opposite sign, the first mode is in phase opposition in variables x
2
and x
3
. Thus,
in addition to providing information on system stability, a knowledge of the modes and the mode
shapes provide considerable insight into the character of the system response.
