Mrinal K Pal. Power system stability
Подождите немного. Документ загружается.

NUMERICAL SOLUTION OF THE TRANSIENT STABILITY PROBLEM
4-9
(a) Since all the non-generator buses are eliminated, the resulting admittance matrix is usually
full. (In contrast, the original bus admittance matrix is usually extremely sparse.) In dealing
with a large system containing many synchronous machines, the computation can become
unnecessarily time consuming.
(b)
In applying the network reduction technique, all the loads are converted into fixed
impedances. While this is valid for certain types of loads, for other types of loads this
assumption may be grossly erroneous. In order to be able to model the loads more
accurately, the load buses must be retained in the network.
(c)
Information on voltages at many of the non-generator buses may be required for
computation of power flow on the transmission lines in order to simulate relay operation and
line tripping during stability computation.
In order to achieve the above objectives and also to take advantage of the network sparsity, it is
advisable to work with the network in the intact form. Portions of the system may be reduced and
unwanted buses eliminated provided network sparsity is not significantly affected.
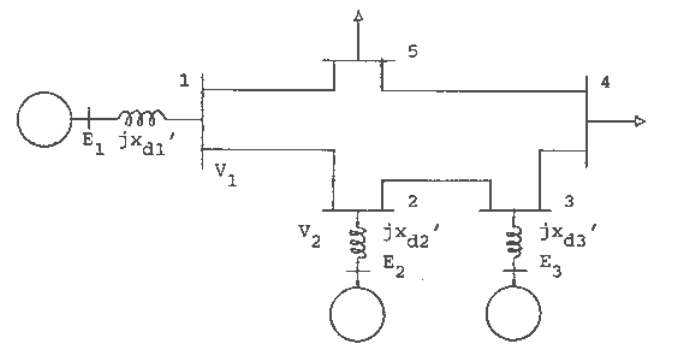
The system shown in Figure 4.2 will be used to illustrate the stability computation when non-
generator buses including load buses are retained. In the five bus system shown, there are
generators at buses numbered 1, 2 and 3 and loads at buses numbered 4 and 5. A procedure for
working with the full network has been discussed in some detail in Chapter 3. Here the relevant
steps will be repeated.
Fig. 4.2 A five bus, three machine system.
The bus currents and voltages are related by
I = YV (4.27)
where
Y is the network admittance matrix, V is the vector of bus voltages and I is the vector of
injected currents.
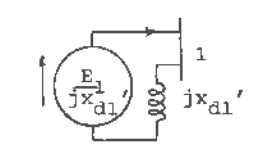
The machines are represented by constant voltage magnitudes behind transient reactances. These
can be replaced by current sources as illustrated in Figure 4.3. Therefore, the currents injected
at buses 1, 2 and 3 would be
2211
/,/
dd
xjExjE
′
′
, and
33
/
d
xjE
′
, respectively, where E
1
, E
2
, and
E
3
are the machine internal voltages and
1d
x
′
, etc. are the transient reactances.
NUMERICAL SOLUTION OF THE TRANSIENT STABILITY PROBLEM
4-10
Fig. 4.3 Machine 1 replaced as a current source.
The network admittance matrix would be modified by including the shunt elements. For
example, the element Y
11
would be modified to
11111
/1
d
xjYY
′
+
=
′
Similar modifications will apply to Y
22
and Y
33
.
If loads are represented as constant impedances, these would be included in the network
admittance matrix by modifying the corresponding elements of the matrix. The current injection
at the load buses would then be zero.
For non-impedance loads, the corresponding current is computed using an estimate of the bus
voltage which would be updated as improved estimates of the voltages are obtained during the
iterative computation. In the interest of improved convergence, it is advisable to convert the
major part of the non-impedance load into constant impedance and include it into the network
admittance matrix. The injected current corresponding to the remaining portion of the load can
then be adjusted to match the total load.
Equation (4.27) can now be solved by factoring the admittance matrix
Y into upper and lower
triangular matrices, utilizing one of the sparsity oriented triangular factorization techniques, and
then by forward and backward substitution. Since the matrix
Y remains constant unless there is a
change in the network due to a disturbance, etc., it is triangularized only as many times as there
are changes in the network during a stability computation.
The machine currents are computed from
d
xjVEI
′
−
=
/)( (4.28)
and power from
)(Re
*
IEP = (4.29)
The procedure for computing the machine power outputs by the above method and updating by
using the corrector formula of equation (4.25) corresponds to the iterative procedure described
earlier. As before, the solution can also be obtained directly by Newton's method.
Handling of constant current load in network solution during stability computation using
Newton's method
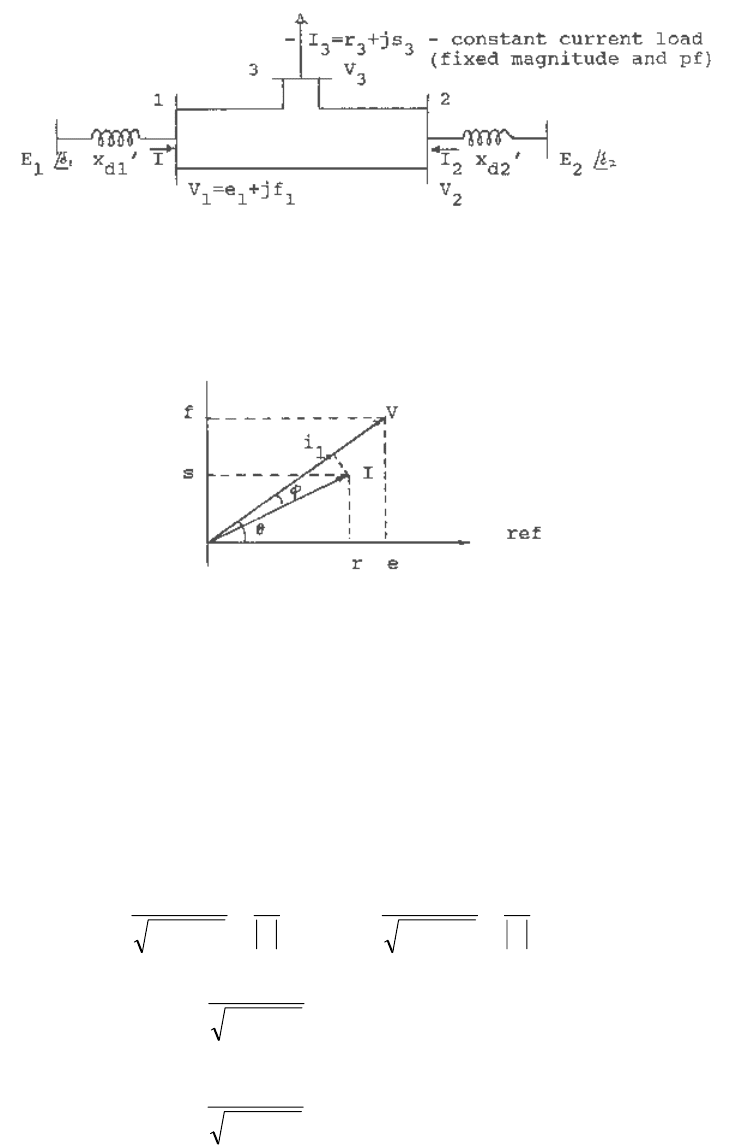
The two machine-three bus system shown in Figure 4.4 will be used to illustrate the handling of
constant current load in stability computation using Newton's method. As explained in Chapter 7,
representation of load by constant current (or power) in stability studies is not recommended.
However, since most commercially available stability programs allow for constant current load
NUMERICAL SOLUTION OF THE TRANSIENT STABILITY PROBLEM
4-11
and loads are frequently represented by constant current in stability studies, a method of handling
constant current load is presented here.
Fig. 4.4 Schematic of a two-machine three-bus system
In the system shown in Figure 4.4, buses 1 and 2 are generator buses and bus 3 is a load bus
having a constant current load. The phase relationship of the voltage and current at bus 3 is
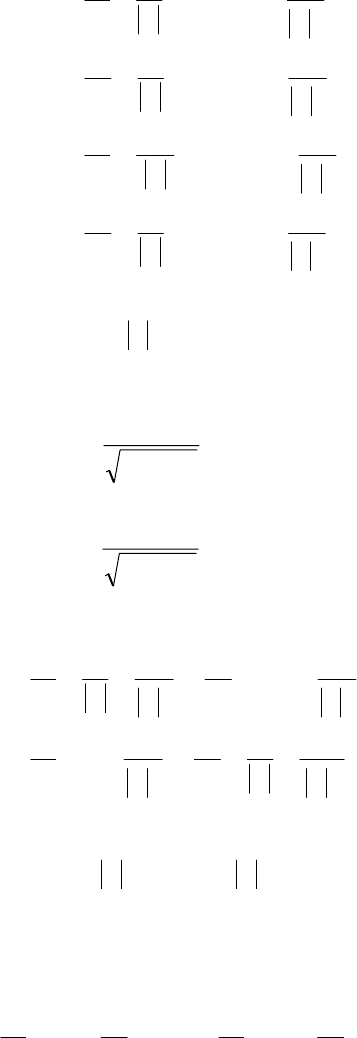
shown in Figure 4.5.
Fig. 4.5 Phasor diagram showing the phase relationship of the current and voltage at bus 3.
We have
=
=
φ
cos
1
Ii constant
=
=
φ
sin
2
Ii
constant
From the phasor diagram,
θθ
θ
θ
cossin
sincos
21
21
iis
iir
−=
+
=
(4.30)
V
f
fe
f
V
e
fe
e
=
+
==
+
=
2222
sin,cos
θθ
22
21
fe
fiei
r
+
+
=
∴
and (4.31)
22
21
fe
eifi
s
+
−
=
NUMERICAL SOLUTION OF THE TRANSIENT STABILITY PROBLEM
4-12
We can compute the partial derivatives as
3
12
1
3
12
2
3
21
2
3
21
1
)(
)(
)(
)(
V
f
fiei
V
i
f
s
V
e
fiei
V
i
e
s
V
f
fiei
V
i
f
r
V
e
fiei
V
i
e
r
−+=
∂
∂
−+
−
=
∂
∂
−
++=
∂
∂
−
++=
∂
∂
(4.32)
If the reactive part of the load is constant impedance, then
BVi −=
2
where B is the load susceptance )/1( XB
−
=
Bf
fe
ei
r −
+
=
∴
22
1
and
Be
fe
fi
s +
+
=
22
1
The partial derivatives are then
3
2
11
3
1
3
1
3
2
11
,
,
V
fi
V
i
f
s
V
efi
B
e
s
V
efi
B
f
r
V
ei
V
i
e
r
−=
∂
∂
−=
∂
∂
−−=
∂
∂
−=
∂
∂
If both real and reactive parts are constant impedances then
BViGVi −==
21
,
where G is the load conductance.
BeGfsBfGer
+
=
−=
∴
,
and
G
f
s
B
e
s
B
f
r
G
e
r
=
∂
∂
=
∂
∂
−=
∂
∂
=
∂
∂
,,,
For the network shown in Figure 4.4, after changing the constant voltage sources into current
sources,
111111
111111
cos)/(sin)/(
)/(
δδ
δ
dd
d
xEjxE
xjEjsrI
′
−
′
=
′
∠
=+=

NUMERICAL SOLUTION OF THE TRANSIENT STABILITY PROBLEM
4-13
(4.33)
222222
222222
cos)/(sin)/(
)/(
δδ
δ
dd
d
xEjxE
xjEjsrI
′
−
′
=
′
∠
=
+=
and, assuming a constant current load at bus 3,
3323133231333
/)(/)( VeifijVfieijsrI −−+−=−−= (4.34)
Also
)()()()(
)()]/1([
331313221212
1111111111
jfejBGjfejBG
jfexBjGjsrI
d
+++++
++
′
−+=+=
)()()()(
)()]/1([
332323112121
2222222222
jfejBGjfejBG
jfexBjGjsrI
d
+++++
++
′
−+=+=
(4.35)
)()()()(
)()](
333333223232
113131333
jfejBGjfejBG
jfeBjGjsrI
+++++
+++=−−=
The above equations can be put into Newton's formulation, after separating the real and
imaginary parts.
∆
∆
∆
∆
∆
∆
′′′′
′
−
′
−−
′
−
−
′
−−−
′
−
−−
′
−−
=
∆
∆
∆
∆
∆
∆
3
3
2
2
1
1
333332323131
333332323131
232322
2
222121
2323
2
22222121
1313121211
1
11
13131212
1
1111
3
3
2
2
1
1
)
1
(
)
1
(
)
1
(
)
1
(
f
e
f
e
f
e
GBGBGB
BGBGBG
GBG
x
BGB
BG
x
BGBG
GBGBG
x
B
BGBG
x
BG
s
r
s
r
s
r
d
d
d
d
(4.36)
where
3
333132313333
3
333132323333
3
333231323333
3
333231313333
/)(/
/)(/
/)(/
/)(/
VffieiViGG
VefieiViBB
VffieiViBB
VefieiViGG
−++=
′′
−+−=
′′
++−=
′
+−+=
′
where i
1
and i
2
are the real and reactive components of the constant current load.
,,
11
sr ∆∆ etc. are computed in the usual way. ,,
11
fe
∆
∆
etc. are obtained by solving equation
(4.36).
NUMERICAL SOLUTION OF THE TRANSIENT STABILITY PROBLEM
4-14
Solution of Faulted Networks
In normal operations power systems are balanced or very nearly so. This means that the three
phases are symmetrical. Therefore, for computational purposes, power systems may be
represented on a single-phase line-to-neutral basis. All the computation procedures presented
earlier are based on the assumption of balanced, symmetrical operations. During a three-phase
fault a power system remains symmetrical and therefore, the single-phase representation remains
valid. Simulation of the fault is accomplished by suitably adjusting the network bus admittance
matrix. For example, if the fault is a three-phase bus-to-ground short circuit, it is simulated
simply by deleting the row and column corresponding to the faulted bus. If the bus fault is
through an impedance it is simulated by adding the fault admittance to the diagonal term
corresponding to the faulted bus. For a fault somewhere along a transmission line, the diagonal
and off-diagonal elements corresponding to the end buses of the faulted line are appropriately
modified. Following the change in the bus admittance matrix that reflects the fault, stability
computations can proceed as described earlier.
During faults other than three-phase, such as line-to-ground, line-to-line or open conductors,
power systems are unsymmetrical, and the single-phase representation is not sufficient. In such
cases the method of symmetrical components is generally used.
In the method of symmetrical components an unsymmetrical set of voltage or current phasors is
resolved into symmetrical sets of components. The unbalanced three-phase system is resolved
into three balanced (symmetrical) systems of phasors called the positive, negative and zero
sequence components. The positive-sequence components have the same phase sequence as the
original phasors. They are equal in magnitude and displaced from each other by 120°. The
negative-sequence components, equal in magnitude and displaced from each other by 120° in
phase, have a phase sequence opposite to that of the original phasors. The zero-sequence
components are equal in magnitude and have zero phase displacement.
Denoting the three phases of the original system by a, b and c, and the symmetrical components
by 1, 2 and 0, the transformation can be expressed in matrix form, for example, for the voltage
phasors, as
=
2
1
0
2
2
1
1
111
a
a
a
c
b
a
V
V
V
aa
aa
V
V
V
or
012
VTV
=
abc
(4.37)
In the above equation the a's are the operators defined by
ooo
01,1201,1201
32
∠=−∠=∠= aaa
so that
111
2
1
,
acab
VaVVaV ==
and
2
2
222
,
acab
VaVVaV ==
Also
000 cba
VVV
=
=

NUMERICAL SOLUTION OF THE TRANSIENT STABILITY PROBLEM
4-15
The reverse transformation is
abc
VTV
1
012
−
= (4.38)
where
=
−
aa
aa
2
21
1
1
111
3
1
T
Similar equations also apply to currents, i.e.,
012
ITI
=
abc
(4.39)
abc
ITI
1
012
−
= (4.40)
The total complex power in the three phases
∗∗∗∗
′
=
′′
=
′
=+
012012012012
3 IVITTVIV
abcabc
jQP
(4.41)
since a and a
2
are complex conjugates
Equation (4.41) shows how complex power can be computed from the symmetrical components
of the voltages and currents in an unbalanced three-phase circuit. In per unit, equation (4.41)
reduces to
∗
′
=+
012012
IVjQP (4.42)
In a balanced three-phase circuit, the three sequences are independent. This means that currents
of each phase sequence will produce voltage drops which are of the same sequence and are
independent of currents of other sequences. In a balanced system, currents of any one sequence
may be considered to flow in an independent network composed of the impedances to the current
of that sequence only. The single-phase equivalent circuit composed of the impedances to current
of any one sequence only is called the sequence network for that particular sequence. It includes
any generated emfs of that sequence.
In order to show the independence of the three sequences consider a balanced static three-phase
circuit with equal self and mutual impedances. The voltage-current relationship can be written in
matrix form as
abcabcabc
IZV
=
(4.43)
with ,and
caacbaabccbbaa
ZZZZZZZ
=
=
=== etc.
Applying the transformation (4.37) to (4.43)
012012012
IZV
=
(4.44)
where
[
]
210
1
012
diag ZZZ
abc
==
−
TZTZ
abaaabaa
ZZZZZZZ
−
=
=
+=
210
,2
NUMERICAL SOLUTION OF THE TRANSIENT STABILITY PROBLEM
4-16
222111000
,,
aaaaaa
IZVIZVIZV
=
=
=
∴
210
,, ZZZ are called the zero-, positive-, and negative-sequence impedances, respectively.
The positive- and negative-sequence impedances of any balanced static three-phase circuit are
equal. For rotating machinery, however, the positive-sequence impedance usually differs from
the negative-sequence impedance because of the interaction between the stator and rotor
windings. The zero-sequence impedance depends on the sign of the mutual impedance in the
original circuit. If the self and mutual impedances are of the same sign, as in the case of a
transmission line or cable, the zero-sequence impedance is higher than the positive- or negative-
sequence impedance. In a three-phase machine, the mutual impedance is of opposite sign from
the self impedance, and the zero-sequence impedance is lower than the positive- or negative-
sequence impedance.
Since the generated voltages are of positive-sequence, the generated power of a synchronous
machine and the synchronizing power between the various synchronous machines of a power
system are positive-sequence power. Therefore, the positive-sequence network is of primary
interest in a stability study.
Analysis of Unsymmetrical Faults
Unsymmetrical faults occur as single line-to-ground faults, line-to-line faults, double line-to-
ground faults, or one or two open conductors. The path of the fault current from line-to-line or
line-to-ground may or may not contain impedance.
For the purpose of analyzing fault at any point in a power system, the system can be replaced by
the Thevenin's voltage in series with a Thevenin's impedance. The phase voltage and current
relationships at the point of fault can then be written in matrix form as
V
abc
= E
abc
– Z
abc
I
abc
(4.45)
where
V
abc
= vector of phase voltages at point of fault
E
abc
= vector of Thevenin or system internal voltage
I
abc
= vector of phase currents flowing out of the system and into the fault
Z
abc
= matrix of the Thevenin impedances, assumed symmetric
In terms of the symmetrical components, equation (4.45) becomes
V
012
= E
012
– Z
012
I
012
(4.46)
In expanded form, equation (4.46) can be written as
−
=
2
1
0
2
1
0
2
1
0
0
0
a
a
a
a
a
a
a
I
I
I
Z
Z
Z
E
V
V
V
(4.47)
210
,, ZZZ are the zero-, negative- and positive-sequence Thevenin inpedances of the respective
sequence networks, measured between point of fault and the reference bus. Note that since the
generated voltages are assumed to be balanced before the fault, 0
20
=
=
aa
EE , and
aa
EE
=
1
.
NUMERICAL SOLUTION OF THE TRANSIENT STABILITY PROBLEM
4-17
Each type of fault can be analyzed using equation (4.47) together with equations that describe
conditions at the fault.
Single line-to-ground fault
For a single line-to-ground fault, assuming the fault is in phase a,
0,0
=
=
=
acb
VII
Therefore, from (4.37) and (4.40),
3/
0
210
210
aaaa
aaa
IIII
VVV
===
=
+
+
which yield, from equation (4.47),
021
1
ZZZ
E
I
a
a
++
=
(4.48)
Line-to-line fault
For a line-to-line fault, assuming the fault is between phases b and c,
cbacb
IIIVV
−
=
=
= ,0,
Therefore, from (4.38) and (4.40),
120
,0
aaa
III
−
=
= ,
21 aa
VV
=
and from (4.47), 0
0
=
a
V (with finite
0
Z )
Therefore, from (4.47),
21
1
ZZ
E
I
a
a
+
=
(4.49)
Double line-to-ground fault
For a double line-to-ground fault
0,0
=
=
=
acb
IVV
Therefore, from (4.38),
021 aaa
VVV
=
=
and from (4.47),
02
02
1
1
ZZ
ZZ
Z
E
I
a
a
+
+
= (4.50)
If the line-to-ground or double line-to-ground fault is through an impedance Z
f
, it can be easily
verified that equations (4.48) and (4.50) apply after modifying the zero sequence impedance to
Z
0
+ 3Z
f
.

NUMERICAL SOLUTION OF THE TRANSIENT STABILITY PROBLEM
4-18
Equations (4.48) to (4.50) suggest that an unbalanced fault can be represented by connecting a
shunt impedance z
f
at the point of fault of the original (positive-sequence) network as shown in
Figure 4.6. The network admittance matrix would be adjusted accordingly. The value of z
f
would
depend on the type of fault as listed in Table 4.1. In Table 4.1, Z
0
and Z
2
are the equivalent zero-
and negative-sequence impedance as viewed from the point of fault.
Fig. 4.6 Representation of unbalanced fault
Table 4.1
Type of fault z
f
3
φ
0
L-G Z
2
+ Z
0
L-L Z
2
L-L-G Z
2
Z
0
/( Z
2
+ Z
0
)
One open conductor
Figure 4.7 shows the section of a transmission line with an open conductor (phase a). The
voltages on the two sides of the opening are as shown.
Fig. 4.7 Section of a transmission line showing an open conductor.
From Figure 4.7 we have
0,0,0
=
′
=
′
=
ccbba
VVI
The voltage and current relationships in terms of symmetrical components would be given by
equation (4.47), except that Z
0
, Z
1
, Z
2
are the zero-, positive-, and negative-sequence impedances
looking into the network at the point of open conductor. (Note that these impedances are
