Mrinal K Pal. Power system stability
Подождите немного. Документ загружается.

SYNCHRONOUS MACHINES
5-19
Locating the d and q axes
Rewriting equations (5.77) as
qdqqqdqdqdq
dqqd
irixEirixixxEe
irixe
−−=−−−−=
−=
)(
(5.80)
where
dqdq
ixxEE )( −−= (5.81)
and then combining them in terms of the complex quantities defined in (5.78)
)()(
qdqqqd
jiijxrjEjee
+
+
−=+ (5.82)
Equation (5.82) shows that by adding the
))((
qdq
jiijxr
+
+
voltage drop to the terminal voltage
)
ˆ
(
qd
jeee += we obtain a quantity E
q
which lies along the quadrature axis and which is related
to the excitation
E by equation (5.81). With the quadrature axis located, i can be resolved into its
d and q components, and
dqd
ixx )( − added to E
q
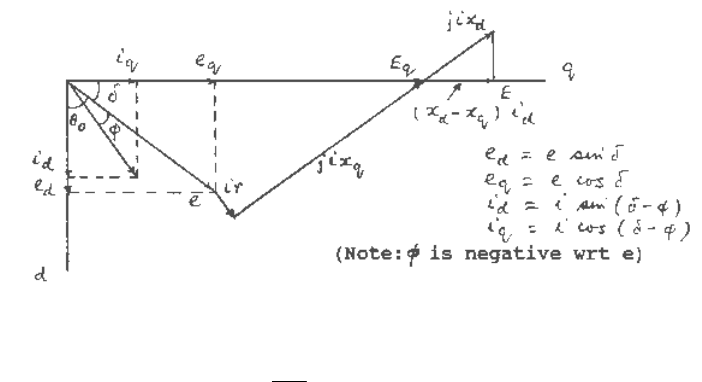
to find E. The complete procedure is illustrated
in Figure 5.2
Fig. 5.2 Steady-state phasor diagram of a synchronous generator.
Note that the relationship
fd
fd
ad
fdad
e
r
x
ixE == (see equations 5.76 and 5.77) is true only in the
steady state.
Open-circuit operation
Under open-circuit condition
0
==
qd
ii
∴
eixEEe
fdadqq
=
=
==
(5.83)
and
e
d
= 0
It may be noted that the quantity
x
ad
i
fd
(= E) in per unit has a magnitude comparable to that of
voltage. Hence, rather than dealing with per unit field current,
i
fd
, it is convenient and customary
to deal with
x
ad
i
fd
in per unit.

SYNCHRONOUS MACHINES
5-20
In the per unit system adopted here, in order to have reciprocal mutuals, the volt-ampere base of
the field had to be equal to the three phase stator volt-ampere base. Since in actual operation the
field volt-ampere is in the order of 0.5% of the stator volt-ampere, the value of per unit
e
fd
for
typical operating condition would be in the order of 0.005pu. A new per unit field voltage is
therefore defined as
fd
fd
ad
fd
e
r
x
E = (5.84)
This new variable is proportional to the original per unit field voltage
e
fd
. We now have the
following steady state relationship
fd
fd
ad
fdadfd
e
r
x
ixEE === (5.85)
With the variable
E defined as E = x
ad
i
fd
(see equation 5.77), it can be seen that when i
fd
= 1/x
ad
,
E = 1.0 pu. On open-circuit, neglecting saturation , when E = 1.0, e
a
(per unit terminal voltage) =
1.0.
E is proportional to the field current, not to the field voltage, except in the steady state.
Reactive Power
qqdd
ieieP +=
From Figure 5.2, we can write
φ
φ
δ
δ
φ
δ
δ
cos)cos(cos)sin(sin ieieieP
=
+
+
+=
Since the phase displacement between
e
ˆ
and i
ˆ
is the same as that between the phase quantities,
we can write, from the definition of reactive power,
]sin)cos(cos)[sin()sin(sin
δ
φ
δ
δ
φ
δ
δ
φ
δ
φ
+
−
+
=
−
+== ieieieQ
=
e
q
i
d
– e
d
i
q
(5.86)
∗
=−+=−++=+
∴
ieijiejeieiejieiejQP
qdqdqddqqqdd
ˆ
ˆ
)()()()( (5.87)
Subtransient and Transient Reactances and Time Constants
In this discussion only one damper winding on each axis is assumed. With all rotor circuits short
circuited, let voltages be suddenly applied to the stator so that only
d axis current flows.
Immediately after the voltage applied, the flux linkages
ψ
fd
and
ψ
11d
cannot change and so are
still zero. Therefore, from (5.61) and (5.62), at
t = 0
+
,
ddafdafdddd
ixixix
11
+
+
−=
ψ
(5.88)
ddffdffddafdfd
ixixix
11
0
+
+
−
==
ψ
(5.89)
ddfddfddad
ixixix
111111
0
+
+
−
==
ψ
(5.90)
Obtaining
i
fd
and i
11d
in terms of i
d
from (5.89) and (5.90), and substituting in (5.88),

SYNCHRONOUS MACHINES
5-21
d
dfffdd
daffdafddadfafdd
dd
i
xxx
xxxxxxx
x
−
+−
−−=
2
111
2
111
2
11
2
ψ
Since subtransient inductance (reactance) is defined as the initial flux linkage per unit of stator
current, the
d axis subtransient reactance is given by
2
111
2
111
2
11
2
dfffdd
daffdafddadfafdd
dd
xxx
xxxxxxx
xx
−
+−
−=
′′
(5.91)
Using the relationships (5.57), the above can also be written as
dfddfdad
dfdad
ld
xxxxx
xxx
xx
11
1
)( ++
+=
′′
(5.92)
Damper winding currents decay much faster than the field winding current. The
d axis transient
reactance is obtained by assuming that the damper winding current has decayed to zero while the
field flux linkage is still zero. Thus
fdafdddd
ixix
+
−=
ψ
(5.93)
fdffddafdfd
ixix
+
−
== 0
ψ
(5.94)
Obtaining
i
fd
from (5.94) and substituting in (5.93)
d
ffd
afd
dd
i
x
x
x
−−=
2
ψ
Thus, the transient reactance is
ffd
afd
dd
x
x
xx
2
−=
′
(5.95)
which can also be written as
fdad
fdad
ld
xx
xx
xx
+
+=
′
(5.96)
The
q axis subtransient reactance can be obtained in a similar manner. At t = 0
+
qqaqqq
ixix
11
+
−=
ψ
(5.97)
qqqqaq
ixix
11111
0
+
−
=
=
ψ
(5.98)
Obtaining
i
1q
from (5.98) and substituting in (5.97)
q
q
qa
qq
i
x
x
x
−−=
11
2
1
ψ
Thus
q
qa
qq
x
x
xx
11
2
1
−=
′′
=
qaq
qaq
l
xx
xx
x
1
1
+
+
(5.99)

SYNCHRONOUS MACHINES
5-22
Since we have assumed one damper winding on the q axis and since there is no q axis field
winding, the
q axis transient reactance is the same as the q axis synchronous reactance. In round
rotor machine, due to the multiple paths of circulating eddy currents, it may be necessary to
consider more than one damper winding on the
q axis. Then there will be distinct q axis
subtransient, transient, and synchronous reactances.
Time constants
To obtain the
d axis open circuit time constants, consider a voltage applied to the field with the
stator open circuited. Since
i
d
= 0, we can write the rotor flux linkage and voltage equations as
ddffdffdfd
ixix
11
+
=
ψ
(5.100)
ddfddfd
ixix
11111
+
=
ψ
(5.101)
fdfdfdfd
ir
dt
d
e +=
ψ
ω
o
1
(5.102)
ddd
ir
dt
d
111
o
1
0
+=
ψ
ω
(5.103)
At
t = 0
+
,
ψ
1d
= 0, and therefore
d
df
d
fd
i
x
x
i
1
1
11
−= (5.104)
Substituting (5.101) in (5.103), we obtain
ddd
d
fd
df
iri
dt
d
x
i
dt
d
x
111
o
11
o
1
−−=
ωω
(5.105)
Substituting (5.100) in (5.102), and using (5.104) and (5.105),
d
df
fdddffd
d
df
dfffdd
fd
i
x
rxrx
i
dt
d
x
xxx
e
1
1
111
1
1o
2
111
+
−
−
−=
ω
(5.106)
Therefore, the
d axis open-circuit subtransient time constant is
)(
111o
2
111
fdddffd
dfffdd
do
rxrx
xxx
T
+
−
=
′′
ω
Since
r
fd
<< r
1d
, the first term within the parenthesis in the denominator can be neglected, so that
d
ffd
df
d
dffd
dfffdd
do
r
x
x
x
rx
xxx
T
1o
2
1
11
1o
2
111
ωω
−
=
−
=
′′
(5.107)
SYNCHRONOUS MACHINES
5-23
Note that the same expression for
do
T
′
′
can also be obtained from the damper circuit voltage
equation, with the field short circuited. Then, at
t = 0
+
, ∆
ψ
fd
= 0, and
d
ffd
df
fd
i
x
x
i
1
1
∆−=∆ .
Substituting in (5.105)
ddd
ffd
df
d
iri
dt
d
x
x
x
111
2
1
11
o
1
0
∆+∆
−=
ω
from which
d
ffd
df
d
do
r
x
x
x
T
1o
2
1
11
ω
−
=
′′
The
d axis open-circuit transient time constant is obtained by either assuming that the damper
circuit current has decayed to zero or the damper winding is absent. Then we have
fdffdfd
ix=
ψ
and
fdfdfd
ffd
fd
iri
dt
d
x
e +=
o
ω
Therefore, the
d axis open-circuit transient time constant is
fd
ffd
do
r
x
T
o
ω
=
′
(5.108)
The short-circuit time constants can be obtained by assuming that the stator circuits are short
circuited. Thus, to obtain the
d axis short-circuit subtransient time constant,
ddafdafdddq
ixixixe
11
0
+
+
−== (5.109)
(neglecting armature resistance and the
q
ψ
&
term)
ddffdffddafdfd
ixixix
11
+
+
−=
ψ
(5.110)
ddfddfddad
ixixix
111111
+
+
−=
ψ
(5.111)
Substituting
i
d
from (5.109) into (5.110) and (5.111)
d
d
afdda
dffd
d
afd
ffdfd
i
x
xx
xi
x
x
x
1
1
1
2
−+
−=
ψ
(5.112)
d
d
da
dfd
d
afdda
dfd
i
x
x
xi
x
xx
x
1
2
1
11
1
11
−+
−=
ψ
(5.113)
Comparing (5.112) and (5.113) with (5.100) and (5.101), we can write the
d axis short-circuit
subtransient time constant as
SYNCHRONOUS MACHINES
5-24
−
−−
−
−
=
′′
d
afd
ffdd
d
afdda
df
d
da
d
d
afd
ffd
d
x
x
xr
x
xx
x
x
x
x
x
x
x
T
2
1o
2
1
1
2
1
11
2
ω
()
(
)
()
2
1o
2
111
2
11
2
111
2
afdffddd
daffdafddadfafdddfffddd
xxxr
xxxxxxxxxxx
−
+−−−
=
ω
()
−
′′
−
=
ffd
afd
dffdd
ddfffdd
x
x
xxr
xxxx
2
1o
2
111
ω
d
d
do
x
x
T
′
′′
′′
=
(5.114)
The
d axis short-circuit transient time constant is obtained by assuming that the damper circuit is
absent. Then, following the previous steps, the short-circuit transient time constant is
d
ffd
afd
d
fd
ffd
fd
d
afd
ffd
d
x
x
x
x
r
x
r
x
x
x
T
2
oo
2
−
=
−
=
′
ωω
d
d
do
x
x
T
′
′
=
(5.115)
The
q axis open-circuit and short-circuit time constants are obtained in a similar manner.
q
q
qo
r
x
T
1o
11
ω
=
′′
(5.116)
q
q
qoq
x
x
TT
′′
′′
=
′′
(5.117)
Synchronous Machine Models for Stability Studies
The synchronous machine models suitable for stability studies will now be derived. We start
with the voltage and flux linkage equations given by equations (5.59) - (5.62). Although these
equations along with the equation for electrical torque (5.69) can be used directly, they would
require unnecessarily short time step in the numerical integration without corresponding increase
in accuracy. Therefore, except in specialized studies, the equations are simplified by neglecting
the
d
ψ
&
and
q
ψ
&
terms, since their effect is usually small. Neglecting these terms is equivalent to
neglecting the short lived power frequency transients that are observed in the machine variables
immediately following a disturbance. This is also consistent with neglecting the transient terms
SYNCHRONOUS MACHINES
5-25
in transmission line modeling. Their impact on machine stability is not generally appreciable. In
general, they tend to provide some positive damping.
Rewriting the stator and rotor voltage equations (5.59) and (5.60), neglecting the
d
ψ
&
and
q
ψ
&
terms, and noting that for balanced operation
e
o
= i
o
= 0,
ssss
IRΨWV
+
= (5.118)
where
,
=
q
d
s
e
e
V
=
=
q
d
s
q
d
s
i
i
IΨ ,
ψ
ψ
−
−
=
−
=
r
r
s
RW ,
0
0
o
o
ω
ω
ω
ω
and
rrrr
dt
d
IRVΨ +=
o
1
ω
(5.119)
where
−
−
−
=
=
=
=
O
O
O
M
M
M
M
M
M
M
M
M
q
d
fd
r
q
d
fd
r
fd
r
q
d
fd
r
r
r
r
i
i
ie
1
1
1
1
1
1
,,
0
0
, RIVΨ
ψ
ψ
ψ
The flux-linkage equations, (5.61) and (5.62), can be rewritten as
rsrssss
IXIXΨ
+
= (5.120)
rrrsrsr
IXIXΨ
+
= (5.121)
where
=
−
−
=
L
LL
qa
daafd
sr
q
d
ss
x
xx
x
x
1
1
, XX
=
′
−=
LL
L
LLLL
LLLL
LL
LL
q
ddf
dfffd
rrsrrs
x
xx
xx
11
111
1
, XXX
I
r
obtained from equation (5.121) and substituted in (5.120) yields

SYNCHRONOUS MACHINES
5-26
[
]
srsrrsrssrrrsrs
IXXXXΨXXΨ
11 −−
−+= (5.122)
From (5.122) and (5.118),
[
]
srsrrsrsssrrrsrs
IXXXXWRΨXXWV ][
11 −−
−++=
(5.123)
Substituting the expression for
I
r
obtained from equation (5.121) into (5.119)
srsrrrrrrrrr
dt
d
IXXRΨXRVΨ
11
o
1
−−
−+=
ω
(5.124)
The various synchronous machine models suitable for stability studies follow directly from
equations (5.123) and (5.124). A few examples are given below.
Model 1 -- One damper winding on each axis
With one damper winding on each of the
d and q axes we have
=
=
=
=
q
d
s
q
d
s
fd
r
q
d
fd
r
i
i
e
e
e
IVVΨ ,,
0
0,
1
1
ψ
ψ
ψ
=
=
qa
daafd
sr
q
ddf
dfffd
rr
x
xx
x
xx
xx
1
1
11
111
1
, XX
−
−
=
−
−
=
−
−
−
=
r
r
x
x
r
r
r
s
q
d
ss
q
d
fd
r
RXR ,,
1
1
Therefore
−
−
=
−
q
ffddf
dfd
rr
x
xAxA
xAxA
11
1
111
1
1
X
where
)(1
2
111 dfffdd
xxxA −=
−−
=
−
q
qa
afddfdaffddadfafdd
rrsr
x
x
xxxxAxxxxA
11
1
111111
1
)()(
XX
Assuming
o
ω
ω
=
SYNCHRONOUS MACHINES
5-27
−−
−
=
−
)()(
111111
11
1
1
afddfdaffddadfafdd
q
qa
rrsr
xxxxAxxxxA
x
x
XXW
Similarly,
[]
+−+−
−
=−
−
)2(
2
111
2
11
11
2
1
1
daffdafddadfafddd
q
qa
q
rsrrsrss
xxxxxxxAx
x
x
x
XXXXW
Also
−
−
−
=
−
q
q
dffdddf
fddffdd
rrr
x
r
rAxrAx
rAxrAx
11
1
111
111
1
XR
and
−
−
=
−
q
q
qa
dafddfdaffd
fddadfafdd
rsrrr
r
x
x
rxxxxA
rxxxxA
1
11
1
111
1111
1
)(
)(
XXR
Therefore, from (5.123) and (5.124),
+−−
−−
−
−+−
−
=
q
d
daffdafddadfafddd
q
qa
q
dafddfdaffdfddadfafdd
q
q
qa
q
d
i
i
rxxxxxxxAx
x
x
xr
xxxxAxxxxA
x
x
e
e
)2(
)(
)()(
2
111
2
11
11
2
1
1111111
1
11
1
ψψ
ψ
(5.125)
and
−
−
−
−
−
+−
+
=
qq
q
qa
ddfafddaffdd
ddadfafddfd
q
q
q
dffdfddfd
ddffddfdfd
q
d
fd
ir
x
x
ixxxxAr
ixxxxAr
x
r
xxAr
xxAre
dt
d
1
11
1
111
1111
1
11
1
111
1111
1
1
o
)(
)(
)(
)(
0
0
1
ψ
ψψ
ψψ
ψ
ψ
ψ
ω
(5.126)
Equation (5.125) can also be written as

SYNCHRONOUS MACHINES
5-28
′′
′′
−
−
′′
′′
=
q
d
d
q
q
d
q
d
i
i
rx
xr
e
e
e
e
(5.127)
where
d
x
′′
and
q
x
′′
are the d and q axis subtransient reactances given by equations (5.91) and (5.99).
qd
ee
′′′′
and are fictitious voltages behind subtransient reactances. These are proportional to the
various flux linkages as indicated in equation (5.125).
Although equations (5.125) and (5.126) are quite straightforward to implement, often the
machine parameter values used in these equations are not available. Therefore, it may be
desirable to express these in terms of the constants supplied by the manufacturers and as defined
earlier. We will use the relationships in (5.57).
From equations (5.92) and (5.96)
fddfddad
dfdad
ld
xxxxx
xxx
xx
11
1
)( ++
=−
′′
(5.128)
ffd
fdad
ld
x
xx
xx =−
′
(5.129)
Also
ffd
ad
dd
x
x
xx
2
=
′
− (5.130)
Dividing (5.129) by (5.130)
ad
dd
ld
fd
x
xx
xx
x
′
−
−
′
= (5.131)
Subtracting (5.128) from (5.129)
fddfddad
fdadld
dd
xxxxx
xxxx
xx
11
)(
)(
++
−
′
=
′′
−
′
(5.132)
Dividing (5.128) by (5.132)
dd
ldld
d
xx
xxxx
x
′′
−
′
−
′
′
−
′
=
)()(
1
(5.133)
The first of the set of equations (5.126) can be written as, after multiplying both sides by
fd
ad
r
x
,
ddadfafddadddffddadfd
fd
ad
fd
fd
ad
ixxxxxAxxxAe
r
x
dt
d
r
x
)()(
11111111
o
−−−−=
ψψψ
ω
Defining
fdfd
fd
ad
fd
ffd
ad
q
Ee
r
x
x
x
e ==
′
that noting and ,
ψ
,
ddaddadqffddfdq
fd
ffd
ixxAxAexxAEe
dt
d
r
x
1
2
1
2
11
o
−+
′
−=
′
ψ
ω
ddaddadqadfd
ixxAxAexAE
1
2
1
22
)1( −+
′
+−=
ψ
(5.134)
